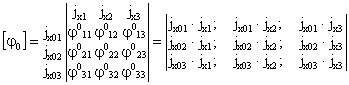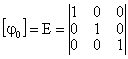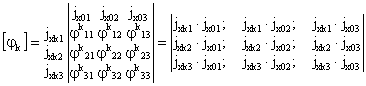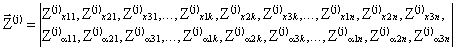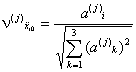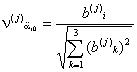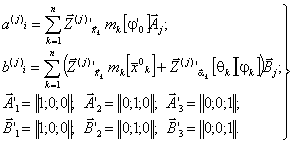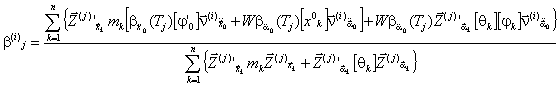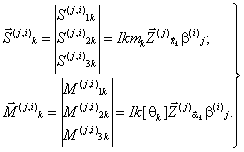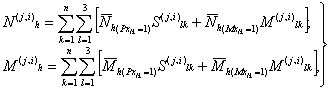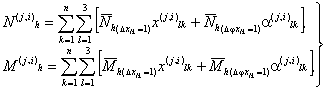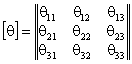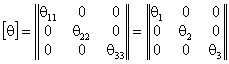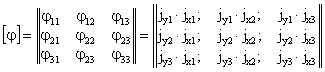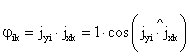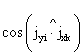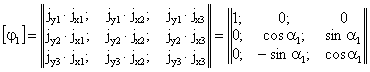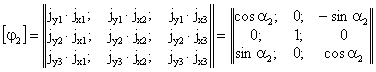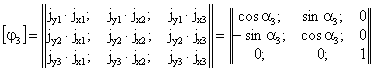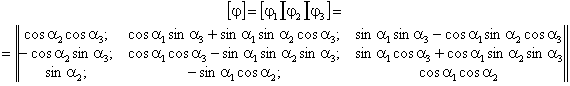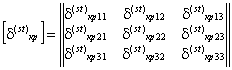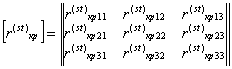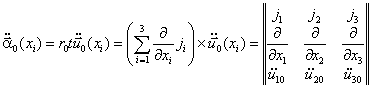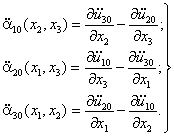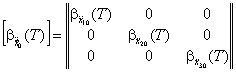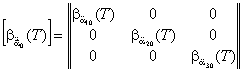
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"Рекомендации Рекомендации по определению расчетной сейсмической нагрузки для сооружений с учетом пространственного характера воздействия и работы конструкций.ОРДЕНА ТРУДОВОГО
КРАСНОГО ЗНАМЕНИ РЕКОМЕНДАЦИИ ПО
ОПРЕДЕЛЕНИЮ Утверждены 11 марта 1988 г. МОСКВА - 1989 Рекомендованы к изданию решением секции «Сейсмостойкость сооружений» Научно-технического совета ЦНИИСК им. В. А. Кучеренко Госстроя СССР. Содержат алгоритм определения расчетной сейсмической нагрузки для сооружений с учетом пространственного характера внешнего воздействия и работы конструкции. В Приложениях приведено обоснование основных положений и методов расчета, приведены примеры расчета сейсмической нагрузки на колонны силосного корпуса и на колонны и диафрагмы жесткости трехэтажного каркасного здания. Предназначены для инженерно-технических работников проектных и научно-исследовательских институтов. ПРЕДИСЛОВИЕРекомендации составлены в развитие СНиП II-7-81 с целью практического использования методов расчета сооружений с учетом пространственного характера работы конструкций и сейсмического воздействия. Рекомендации предназначены для использования в проектной практике при расчете сооружений сложных конструктивных форм, несущих большие нагрузки и требующих учета пространственного характера работы конструкций. В Рекомендациях приведен алгоритм расчета по определению сейсмической нагрузки на сооружения с учетом пространственного характера воздействия и работы самой конструкции. Даны рекомендации по выбору расчетных динамических моделей сооружений и определению их параметров. Приводится алгоритм расчета режима свободных колебаний сооружений. Даны рекомендации по определению расчетных моделей сейсмического воздействия и выбору их численных параметров. Приводится алгоритм расчета вынужденных колебаний сооружения по выбранным моделям внешнего воздействия. В приложениях приведены примеры расчета сейсмической нагрузки на колонны силосного корпуса и расчета сейсмической нагрузки на колонны и диафрагмы жесткости трехэтажного каркасного здания. Изложены основные положения расчета по определению сейсмической нагрузки с учетом пространственного характера работы сооружения и сейсмического воздействия. По методике настоящих Рекомендаций разработана автоматизированная система расчета сооружений на сейсмические воздействия «Полифем-S87». Рекомендации разработаны в Отделе сейсмостойкости сооружений ЦНИИСК им. В. А. Кучеренко (основной текст - канд. техн. наук Ю. П. Назаров при научном руководстве д-ра техн. наук проф. Н. А. Николаенко, приложения 1, 2 - кандидаты техн. наук А. Т. Штоль и Г. В. Мамаева; приложение 3 - инж. А. Ш. Ревишвили). ОБЩИЕ ПОЛОЖЕНИЯ1.1. Настоящие Рекомендации составлены в развитие СНиП II-7-81 [17] с целью практического использования методов расчета сооружений с учетом пространственного характера работы конструкций и сейсмического воздействия. Анализ последствий землетрясений (повреждения и разрушения сооружений) показывает, что движения (колебания) отдельных конструкций происходят одновременно по нескольким направлениям, т.е. эти движения являются пространственными. Перекрытия зданий перемещаются в двух направлениях и вращаются относительно вертикальной оси, что приводит к более интенсивным повреждениям периферийных несущих конструкций, т.е. сооружение работает как единая пространственная динамическая система. Анализ регистрации движений грунта при землетрясениях показывает, что они являются сложными многомерными (пространственными) процессами. Сложность пространственного характера сейсмического воздействия состоит в том, что оно представляет собой поле движений грунта, определенное сейсмическими волнами с конечной скоростью их распространения. Сейсмические волны не являются монохроматическими, а представляют спектр одноименных волн различной длины, доминирующих в различные интервалы времени землетрясения. В начальные моменты времени приходят, имеющие большую скорость распространения, продольные Р-волны, затем - поперечные S-волны с меньшей скоростью распространения, но с большей интенсивностью воздействия. После S-фазы генерируются поверхностные L-волны (Рэлея-Лэмба и Лява), которые имеют еще меньшую скорость распространения. Наиболее сильные повреждения и разрушения сооружений наблюдаются при более интенсивных фазах движения грунта, определяемых спектрами S- и L-волн. Такое поле движений приводит к дилатации и ротации массива грунта в основании сооружений. Дилатация (изменение объема за счет его расширения-сжатия) массива грунта в основании сооружения определяется всеми видами волн P, S и L и приводит только к поступательным движениям основания сооружения. Эти движения происходят в трех направлениях. Ротация (изменение формы объема за счет его искажения) определяется только вихревыми составляющими поля S- и L-волн и приводит к вращению массива грунтового основания сооружения. Эти вращения происходят относительно трех осей. 1.2. Рекомендации предназначены для использования в проектной практике при расчете сооружений сложных конструктивных форм, несущих большие нагрузки и требующих обязательного учета пространственного характера работы конструкций. Объем таких сооружений в проектной практике постоянно возрастает, поскольку применение новых конструкционных материалов, новых конструкций, обладающих большей несущей способностью, приводит к появлению конструктивных решений сооружений, для которых учет пространственного характера воздействия и работы конструкций является обязательным. 1.3. В Рекомендациях рассматривается упругая стадия работы конструкций при колебаниях, соответствующих малым перемещениям и углам вращения масс сооружения. 1.4. Применение метода рекомендаций связано с обработкой громоздких массивов чисел. Использование рекомендуемых методов требует привлечения ЭВМ. Рекомендации составлены таким образом, что применение ЭВМ в проектной практике возможно в двух формах: а) применение ЭВМ для выполнения отдельных этапов расчета: - статический расчет сооружения с целью определения единичных внутренних усилий, формирования матрицы жесткости или податливости системы в целом; - вычисления собственных значений матриц жесткости или податливости сооружения при определении частот и форм колебаний; - определение параметров сейсмического воздействия; - расчет режимов вынужденных колебаний и определение фактических величин внутренних усилий в конструкциях сооружения и т.д.; б) объединение отдельных этапов работ в единый комплекс расчетов и разработка автоматизированной системы расчета сооружений с учетом пространственного характера работы конструкций и сейсмического воздействия. 2. АЛГОРИТМ РАСЧЕТА ПО ОПРЕДЕЛЕНИЮ СЕЙСМИЧЕСКОЙ НАГРУЗКИ НА СООРУЖЕНИЯ С УЧЕТОМ ПРОСТРАНСТВЕННОГО ХАРАКТЕРА ВОЗДЕЙСТВИЯ И РАБОТЫ КОНСТРУКЦИЙ2.1. В Рекомендациях приводится алгоритм определения сейсмической
нагрузки на сооружения в наиболее простом варианте, т.е. без учета всех
корреляционных связей при компонентной форме представления векторов сейсмического
воздействия - выбор и определение параметров расчетной динамической модели сооружения; - формирование матриц жесткости или податливости и определение единичны усилий в элементах конструкций; - расчет режима свободных колебаний; - определение
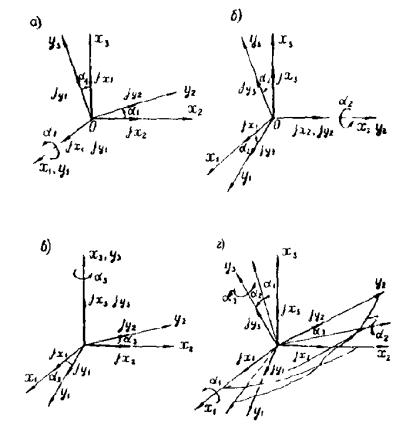
расчетных параметров векторов сейсмического воздействия - расчет режима вынужденных колебаний; - определение расчетных усилий в поперечных сечениях несущих конструкций сооружений. *) Структура алгоритма расчета сооружений как единых пространственных систем на сейсмические воздействия с учетом пространственного характера возмущения зависит от ряда факторов: способа представления информации о векторах сейсмического воздействия; учета корреляции между отдельными формами колебаний; учета корреляции между векторами сейсмического воздействия и их компонентами. Расчет колебаний сооружений в соответствии с принятым алгоритмом выполняется на ЭВМ. На каждом отдельном этапе расчет сводится к заполнению и дальнейшей обработке соответствующих таблиц, перечень которых приводится ниже. Расчет сводится к определению сейсмической нагрузки для выборочных элементов конструкций или для определения внутренних усилий в выборочных поперечных сечениях. Набор сечений, подлежащих проверке, устанавливается проектировщиком в зависимости от конструктивной схемы сооружения. Рекомендуется проверять наиболее напряженные периферийные конструктивные элементы, а для сравнения целесообразно выполнять проверку менее напряженных центральных элементов. Выбор расчетной динамической модели сооружения и определение ее параметров- конструкции сооружения (перекрытия, отдельные конструктивные части и т.д.), жесткость которых на порядок больше жесткости других конструкций, считаются абсолютно твердыми; - другие конструкции сооружения (элементы каркаса, ядра и диафрагмы жесткости, диафрагмы лестничных клеток и т.п.) считаются упругими связями с линейными диаграммами деформирования материала; - в динамических моделях массы сооружения распределяются по абсолютно твердым телам, а упругие конструкции считаются невесомыми и их масса относится к соответствующим твердым элементам, т.е. динамическая модель сооружения представляется в виде отдельных (дискретных) абсолютно твердых тел, соединенных несущими невесомыми упругими элементами; - фундамент сооружения в расчетной динамической модели принимается жестким и моделируется твердым телом. 2.3. Дискретно расположенные в динамической модели массы могут быть представлены: - материальной точкой, которая может иметь максимум три степени свободы и характеризуется величиной массы mk (k = 1, ..., n); - твердым диском, имеющим три степени свободы и учитывающим геометрию распределения масс и упругих связей в плоскости диска. Диск движется в своей плоскости и характеризуется величиной массы mk и центральным осевым моментом инерции θk относительно оси, перпендикулярной к плоскости диска; - массой в виде твердого тела, имеющего шесть степеней свободы и учитывающего геометрические параметры распределения масс и упругих связей в пространстве. Инерционные параметры твердого материального тела характеризуются величиной массы mk и тензором инерции масс относительно каких-либо осей [θk] (k = I, II, ..., n); в расчетах в качестве таких осей следует принимать главные и центральные оси инерции тела, для которых [θk] имеет вид диагональной матрицы с отличными от нуля только осевыми моментами инерции масс θik (i = 1, 2, 3). Величины масс mk определяются в соответствии с требованиями учета нагрузок, изложенными в п. 2.1 СНиП II-7-81; моменты инерции масс θik вычисляются по справочным данным. 2.4. Материал несущих конструкций сооружения (деформируемые связи) принимается упругим с линейной диаграммой деформирования. Модели этих конструкций (колонны, панели, диафрагмы и т.п.) определяются: - видом представления масс (точка, диск, тело) в расчетной динамической, модели сооружения; - моделями упругих связей в статической расчетной модели при формировании матриц жесткости (или податливости). 2.5. При геометрическом описании расчетных динамических моделей сооружения вводятся системы отчета и устанавливается связь между ними: - вводится инерциальная система осей ОХ1X2Х3 без привязки начала отсчета. В качестве этой системы осей может быть принята ориентация по странам света или какая-либо другая местная система трех ортогональных направлений; - вводится система отсчета Ox01x02x03, связанная с подвижным основанием (фундаментом), движение которого определяется моделью сейсмического воздействия; оси Ox01x02x03 рекомендуется совмещать с основными осями здания; - взаимосвязь между введенными системами осей определяется матрицей [φ0], имеющей следующий вид: где φ0ij - скалярные произведения единичных векторов jx0i и jxi (орт систем осей Ox01x02x03 и ОХ1Х2Х3); точкой отмечен знак скалярного произведения, поэтому φ0ij являются тригонометрическими функциями углов между осями ОХ1Х2Х3 и Ox01x02x03; если системы отсчета ОХ1Х2Х3 и Ox01x02x03 одинаково ориентированы в пространстве (оси параллельны), то оператор (1) сводится к единичной матрице:
- однозначно и произвольно устанавливается нумерация инерционных элементов (материальных точек, дисков, тел) расчетной динамической модели сооружения I, II, III, ..., k, ..., n; - с каждым из инерционных элементов неизменно связываются системы осей kxk1xk2xk3. Для дисков и твердых тел эти оси должны быть главными и центральными осями инерции масс; - определяется взаимосвязь между введенными системами осей kxk1xk2xk3 и Ox01x02x03. Эта взаимосвязь устанавливается с помощью операторов [φk], имеющих вид: где φkij - скалярные произведения орт jx0i и jxkj системы осей Ox01x02x03 и kxk1xk2xk3, поэтому φkij вычисляются аналогично (1); в частности, если оси kxk1xk2xk3 и Ox01x02x03 ориентированы в пространстве одинаково, то [φk] = Е - единичная матрица; - векторами Описание упругих свойств расчетной динамической модели сооружения2.6. Упругие свойства динамической модели сооружения определяются матрицей жесткости [r] или податливости [δ], которые рассчитываются по любым известным методам строительной механики. 2.7. Если расчет выполняется по методу сил (определение [δ]), то в центрах масс по направлению осей системы отсчета (или относительно их) последовательно прикладываются единичные силы Pxik = 1 (или моменты Мxik = 1). От последовательного действия каждой единичной силы или момента выполняется статический расчет упругой системы. При этом для поперечных сечений упругих элементов определяются внутренние усилия, которые сводятся в табл. 1. Определяются также перемещения начал всех систем отсчета по направлению принятых осей и углы поворота данных систем отсчета относительно этих осей. В соответствии с принятой нумерацией масс из этих перемещений и углов поворота формируется матрица податливости системы [δ]. Результаты сводятся в табл. 2. Таблица 1 Таблица 2 Таблица 3 Таблица 4 2.8. Если расчет упругой системы выполняется по методу перемещений, то на начало выбранных систем отсчета по направлению принятых осей (или относительно их) накладываются связи, которым последовательно сообщаются единичные перемещения Δxik = 1 (или углы поворота Δφik = 1). Последовательно от каждого из этих перемещений или углов поворота выполняется статический расчет принятой упругой системы. При этом для поперечных сечений упругих элементов определяются внутренние усилия, которые сводятся в табл. 3. Определяются также реакции во всех наложенных связях. Из этих реакций, в соответствии с принятой нумерацией масс, формируется полная матрица жесткости системы [r]. Результаты формирования матрицы [r] сводятся в табл. 4. Расчет режима свободных колебаний2.9. Выполняется вспомогательный анализ полных матриц [r] [δ-1]. Для выявления особенностей составляющих где Таблица 5 Анализ (3) и (4) является необходимым, но недостаточным для определения частот и форм колебаний системы. 2.10. Выполняется анализ полных матриц [А] = [M-1][r] или [B] = [А-1] = [δ][M] для выделения обособленных составляющих
Здесь [Mi] - полная матрица инерционных параметров системы, структура которой показана в табл. 5, а [Mi] - ее составляющие, соответствующие обособленным составляющим [ri] или [δi]. 2.11. Отдельно для каждой из обособленных составляющих [Аi] или [Bi] (если они имеются) решается задача на собственные значения (собственные числа и векторы) по частотным уравнениям. Для каждой системы эти уравнения в прямой или обратной форме имеют соответственно вид: где
блочный вектор коэффициентов j-ой формы колебаний. Если обособленные составляющие [Ai] или [Bi] отсутствуют, то все колебания в пространстве линейно взаимосвязаны и задача решается по полной матрице [А] или [B]. При решении прямой задачи (7) по [A] определяются собственные числа в виде Ω2j (Ωj - частота j-ой формы колебаний), а при решении обратной задачи (8) по [B] - собственные значения - 1/Ω2j. Каждая из обособленных составляющих [Ai] или [Bi] описывает свою независимую группу колебаний. Результаты решения задачи по определению форм и частот сводятся в соответствующие таблицы (табл. 6). Такие таблицы составляются для каждой обособленной матрицы [Аi] или [Bi]. 2.12. Коэффициенты форм колебаний системы нормируются по отношению к одному какому-либо коэффициенту, принимая его значение за единицу. В качестве такого нормирующего множителя удобно принимать значение коэффициента перемещения I массы в направлении 1-ой оси - Z(j)x11 = 1. 2.13. Критерием точности вычислений коэффициентов форм колебаний является удовлетворение их условиям ортогональности, имеющим вид При проверке условий ортогональности строится матрица [С], компоненты которой Cij определяются по (9) и при i = j, Cii = Mi (Мi - приведенная к i-ой форме колебаний масса сооружений). Результаты проверки ортогональности форм колебаний сводятся в табл. 7.
Таблица 7
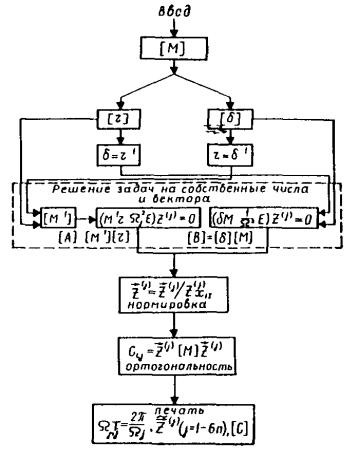
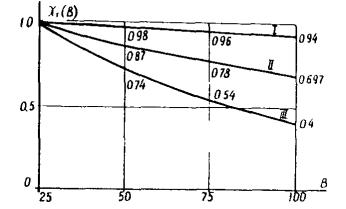
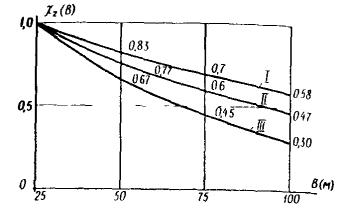
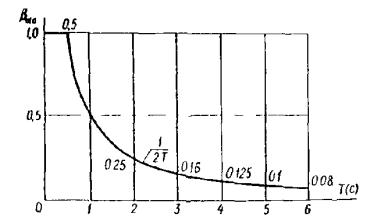
Проверка условий ортогональности выполняется для каждой самостоятельной группы колебаний, определяемой соответствующими обособленными составляющими [Ai] или [Вi]. Весь алгоритм расчета режима свободных колебаний целесообразно выполнять по структуре, программы вычислений, показанной на рис. 1. Рис. 1. Структура программы расчета режима собственных колебаний динамической системы Расчетные параметры сейсмического воздействия2.14. В соответствии с расчетной балльностью площадки строительства по СНиП II-7-81, определяется независимая от пространственной ориентации (инвариантная) расчетная интенсивность ускорений поступательного движения грунта в основании сооружения. Расчетная инвариантная интенсивность ускорений поступательного движения грунта I является функцией от меньшего размера сооружения в плане В и вычисляется по формуле I(В) = gАχ1(В) (м/с2), (10) где g ≈ 10 м/с2 - ускорение силы тяжести; А - коэффициент, принимаемый равным 0,1; 0,2; 0,4 для расчетной сейсмичности 7, 8 и 9 баллов по СНиП II-7-81. Значение нормированной аппроксимирующей функции χ1(В) определяется по ее графикам рис. 2 или вычисляется по формуле χ1(В) = eα(B - 25), (11) где В(м) - меньший размер сооружения в плане; α - аппроксимирующий коэффициент, значение которого равно -8 · 10-4; -4,8 · 10-3 и -1,2 · 10-2 (1/м) для I, II и III категории грунтов по СНиП II-7-81. Рис. 2. Графики нормированных функций χ1(В) = eα(B - 25) при α = -8 · 10-4; -4,8 · 10-3 и -1,2 · 10-2 (1/м) для I, II и III категорий грунтов, соответственно 2.15. В зависимости от категории грунтов по СНиП II-7-81 определяется независимая от пространственной ориентации (инвариантная) интенсивность угловых ускорений вращательных движений грунта в основании сооружений (ускорения ротации поля сейсмических движений). Этот инвариант интенсивности определяется относительной (по отношению к инварианту ускорения поступательного движения) величиной W. Расчетное значение относительного инварианта интенсивности углового ускорения сейсмических движений грунта является функцией от меньшего размера сооружения в плане В и вычисляется по формуле где Значение нормированной аппроксимирующей функции χ2(В) определяется по графикам рис. 3 или вычисляется по формуле χ2(В) = eb(B - 25), (13) где В(м) - меньший размер сооружения в плане; b - аппроксимирующий коэффициент, значение которого равно -7,2 · 10-3; -1 · 10-2 и -1,6 · 10-2 (1/м) для I, II и III категорий грунтов по СНиП II-7-81. Рис. 3. Графики нормированных функций χ2(В) = eb(B - 25) при b = -7,2 · 10-3; -1 · 10-2 и -1,6 · 10-2 (1/м) для I, II и III категорий грунтов, соответственно 2.16. Спектральный состав компонент векторов сейсмического воздействия (ускорения поступательного движения Для вектора ускорения поступательного движения грунта значения коэффициента динамичности определяются по СНиП II-7-81 и вычисляются по формуле где kгр - коэффициент, учитывающий категорию грунтов по СНиП II-7-81, значения которого принимаются по данным табл. 8. Таблица 8
Таблица 9
Рис. 4. Графики
нормированных коэффициентов динамичности вектора ускорения поступательного движения сейсмического воздействия Потери энергии при колебаниях системы учитываются коэффициентом αγ, значения которого определены для (14) в соответствии со СНиП II-7-81 и приведены в табл. 9. Значения
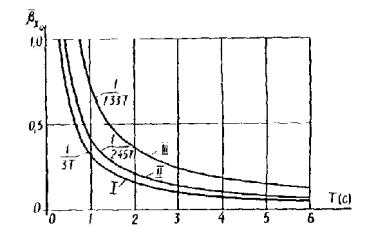
нормированных по соответствующим максимумам коэффициентам динамичности для I категории грунтов для II категории грунтов для III категории грунтов Для вектора углового ускорения вращения сейсмического воздействия значения коэффициента динамичности вычисляются по формуле где kгр - коэффициент, учитывающий категорию грунтов по СНиП II-7-81, значения которого определяются по табл. 8.
Примечание. Для других значений γ допускается коэффициент bγ определять по интерполяции. Значения коэффициента bγ, учитывающего потери энергии при колебаниях системы, определяются по табл. 10. Нормированные
значения коэффициентов динамичности
Рис. 5. График нормированного коэффициента динамичности вектора углового ускорения вращения сейсмического воздействия 2.17. Сейсмическое воздействие имеет произвольное направление в пространстве (см. п. 2.3 СНиП II-7-81). Ориентация в пространстве векторов ускорения поступательного движения и углового ускорения вращения грунтового основания сооружения определяется направляющими косинусами. Вектор ускорения
поступательного движения грунта в основании сооружения
задается в инерциальных осях ОХ1Х2Х3,
в качестве которых, в соответствии с п. 2.5, может быть принята ориентация по
сторонам света или какая-либо другая местная
система трех ортогональных направлений. Ориентация в пространстве вектора Вектор углового
ускорения вращения грунта задается в осях Оx01,x02x03,
неизменно связанных с основанием сооружения. В качестве осей Оx01x02x03, согласно п. 2.5, следует принимать систему главных осей сооружения.
Ориентация в пространстве вектора Расчетные
параметры ориентации векторов сейсмического воздействия проверочные (наиболее вероятные для заданного региона строительства) и основные расчетные. Расчет на
наиболее вероятные значения направляющих косинусов является проверочным и выполняется
в тех случаях, когда они известны для данного региона строительства. Эти значения Расчет на
основные значения направляющих косинусов Основные расчетные значения направляющих косинусов вычисляются отдельно для каждой из учитываемых форм колебаний, исходя из условий максимума динамической реакции по рассматриваемой форме колебаний. Эти значения направляющих косинусов для j-ой формы колебаний определяются по следующим формулам: где Результаты вычислений расчетных значений направляющих косинусов сводятся в табл. 11. Таблица 11 Расчет режима вынужденных колебанийгде
Таблица 12 Максимальное значение коэффициента динамичности (24) имеет место при i = j, т.е. β(i)j < β(j)j при i ≠ j. Результаты вычислений коэффициентов динамичности сводятся в табл. 12. 2.19. Если расчет упругой системы выполняется по методу сил и в соответствии с требованиями п. 2.7 выполнялось построение матрицы податливости [δ] (см. табл. 2), а также вычислялись внутренние усилия в поперечных сечениях элементов от единичной нагрузки (см. табл. 1), то основными расчетными параметрами являются векторы сейсмических сил и моментов, которые определяются по следующим формулам: Коэффициент k в (25) соответствует k1 СНиП II-7-81, значения которого согласно табл. 3 СНиП II-7-81 предназначены для сооружений симметричных в плане, а так же для зданий регулярной конструктивной схемы, когда эффектами пространственной работы конструкций можно пренебречь. Для сооружений промышленного или гражданского назначения, имеющих сложную конструктивную схему, необходим учет пространственной работы конструкций. В этих случаях значения коэффициента k отличаются от соответствующего значения k1 по СНиП II-7-81. Поэтому значение коэффициента k следует принимать по специальному обоснованию в соответствии с принятой конструктивной схемой сооружения и ее возможностями к развитию пластических деформаций и местных повреждений, не приводящих к выходу из строя сооружения в целом. Предварительное значение коэффициента k должно задаваться в задании на проектирование и затем корректироваться в ходе выполнения проектных работ и уточняться в соответствии с выбранной конструктивной схемой с последующим окончательным утверждением заказчиком. Значения векторов сейсмических сил и моментов вычисляются для каждой из рассчитываемых форм колебаний и по каждому варианту ориентации векторов воздействия. Для каждой формы колебаний максимальные значения векторов сил и моментов определяются при значениях направляющих косинусов по (22). Результаты расчета сводятся в табл. 13. Таблица 13
Таблица 14
2.20. Если расчет упругой системы выполняется по методу деформаций и в соответствии с требованиями п. 2.8 выполнялось построение матрицы жесткости [r] (см. табл. 4), а также вычислялись внутренние усилия в поперечных сечениях упругих элементов от единичных перемещений, то основными расчетными параметрами являются векторы перемещений центров масс и углов вращения масс, которые определяются по следующим формулам: Значения векторов перемещений центров масс и углов поворота масс относительно их центра вычисляются для каждой из рассчитываемых форм колебаний и по каждому варианту ориентации векторов воздействия. Для каждой формы колебаний значения векторов (26) имеют максимальные величины при направляющих косинусах по (22). Результаты этого расчета сводятся в табл. 14. Определение расчетных значений внутренних усилий в поперечных сечениях несущих конструкций сооружения2.21. Если расчет упругой системы выполнялся по методу сил, то для каждой отдельной формы колебаний, по данным п. 2.19, по величинам фактических сейсмических сил и моментов, корректируются внутренние усилия от единичной нагрузки по данным п. 2.7: где N(j,i)1, N(j,i)2, N(j,i)3 - поперечные и
продольные силы по j-ой форме при i-ой ориентации векторов сейсмического воздействия; M(j,i)1, M(j,i)2, M(j,i)3 - изгибающие и
крутящие моменты по j-ой форме при i-ой ориентации
векторов сейсмического воздействия для рассматриваемого сечения Внутренние усилия (27) вычисляются по каждой форме колебаний и для каждого из вариантов ориентации векторов сейсмического воздействия. Для каждой формы колебаний максимум усилий (27) имеет место при значениях направляющих косинусов по (22). Результаты этого расчета сводятся в табл. 15. 2.22. Если расчет упругой системы выполняется по методу деформаций, то для каждой формы колебаний внутренние усилия от единичных перемещений и углов вращения по данным п. 2.8 корректируются на величины фактических перемещений и углов вращения масс по данным п. 2.20: где Таблица 15 Таблица 16 Таблица 17
По (28) внутренние усилия вычисляются для каждой формы колебаний и для каждого варианта ориентации векторов сейсмического воздействия. Максимум усилий для каждой формы колебаний имеет место при значениях направляющих косинусов по (22). Результаты этого расчета сводятся в табл. 16. 2.23. Для каждого i-го варианта
ориентации
векторов сейсмического воздействия по внутренним усилиям, соответствующим отдельным формам колебаний, N(j,i)l и M(j,i)l определяются расчетные значения внутренних усилий где f - число учитываемых форм колебаний при определении расчетных значений внутренних усилий в l-ом направлении (l = 1, 2, 3) поперечного сечения для рассматриваемого i-го варианта ориентации векторов сейсмического воздействия. Результаты расчета сводятся в табл. 17. 2.24. Из расчетных усилий (29),
соответствующих отдельным i-ым вариантам
ориентации векторов сейсмического воздействия, по данным табл. 17 принимаются
максимальные значения
усилий для проверки несущей способности сечений
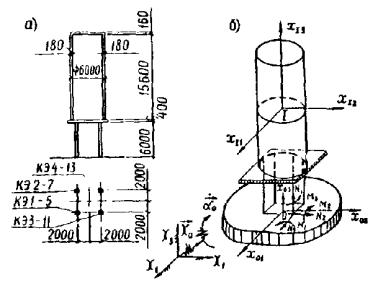
в сочетании с усилиями от других видов нагрузок. Принятый i-ый вариант значений Приложение 1ПРИМЕР РАСЧЕТА ПО ОПРЕДЕЛЕНИЮ СЕЙСМИЧЕСКОЙ НАГРУЗКИ НА КОЛОННЫ СИЛОСНОГО КОРПУСАПриведенный в разделе 2 алгоритм расчета проиллюстрирован на простейшем примере определения нагрузки на колонны силосного корпуса (рис. 6). Параметры сооружения взяты из проекта железобетонного силосного корпуса, разработанного институтом Сибгипробиосинтез (г. Красноярск) для Андижанского гидролизного завода. В соответствии с проектом сечение колонн 0,6×0,6 м. Описание расчетной динамической модели сооружения 1. По п. 2.2, пренебрегая деформациями железобетонного резервуара, примем расчетную динамическую модель в виде твердого цилиндра на упругих стойках, как показано на рис. 6. Нагрузку определим на несущие колонны без учета деформаций резервуара. 2. Согласно п. 2.3 инерционные параметры при полностью заполненном резервуаре равны: m1 = 636 · 103 кг; θ1I = θ2I = 1324 · 104 кг/м2; θ3I = 286 · 104 кг/м2. 3. По п. 2.4 железобетонные колонны моделируем упругими стержневыми конечными элементами с геометрическими характеристиками в соответствии с рис. 6.
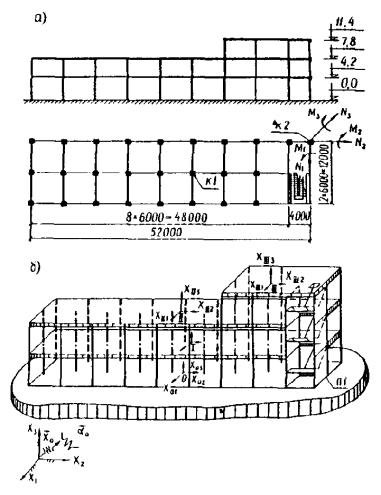
Рис. 6. Конструктивная схема (а) и расчетная динамическая модель (б) силосного корпуса 4. Согласно п. 2.5 определяются геометрические параметры динамической модели: - оси ОХ1Х2Х3 принимаем параллельными осям Ox01x02x03; - начало осей Ox01x02x03 связываем с геометрическим центром фундамента (см. рис. 6); - [f0] = Е - единичная матрица; - твердому цилиндру присваиваем номер 1; - вводим главные центральные оси инерции цилиндра Ix11x12x13; - [φI] = Е; - Описание упругих свойств расчетной динамической модели сооружения 5. По п. 2.6. для статического расчета рассматриваемой упругой системы воспользуемся программами, основанными на конечном элементе. 6. В соответствии с п. 2.7 от последовательного действия единичных сил и моментов выполняем статический расчет и определяем внутренние усилия в рассматриваемых сечениях, а также перемещения центра массы (табл. 1) и углы поворотов цилиндра. В качестве примера в табл. 18 сведены внутренние усилия для нижнего сечения колонны. В табл. 19 сведены единичные перемещения и углы поворотов. Табл. 19 определяет матрицу [δ]. Расчет режима свободных колебаний 7. Согласно п. 2.9 анализ матрицы [δ] (табл. 19) показывает, что она не содержит обособленных составляющих. Таблица 18 Единичные внутренние усилия в нижнем сечении колонны
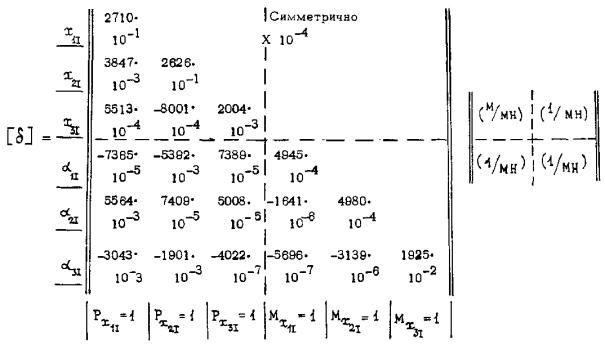
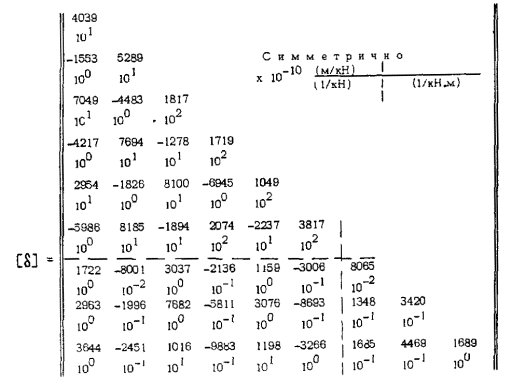
Таблица 19 Матрица податливости Таблица 20 Матрица инерционных параметров Таблица 21 Частоты и коэффициенты колебаний
Таблица 22 Условия ортогональности форм колебаний
8. В соответствии с п. 2.10 матрица инерционных параметров приведена в табл. 20. Матрица [В] = [δ][M] также не содержит обособленных составляющих. 9. По п. 2.11 задача по определению частот и форм колебаний решается по полной матрице [δ] для всей системы. Результаты решения по структуре алгоритма, показанного на рис. 6, сведены в табл. 21. 10. По п. 2.12 коэффициенты форм колебаний (см. табл. 21) нормированы на величину Z(j)x1I = 1 (j = 1 ÷ 6). 11. По п. 2.13 условия ортогональности форм колебаний показаны в табл. 22.
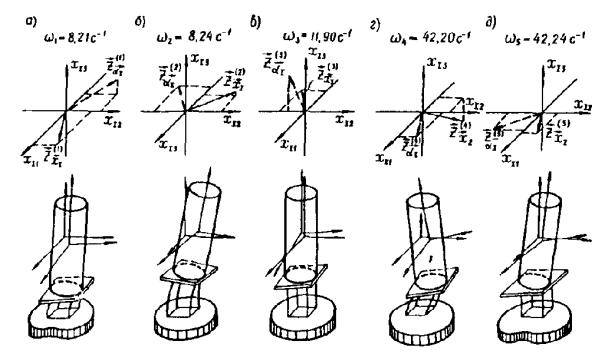
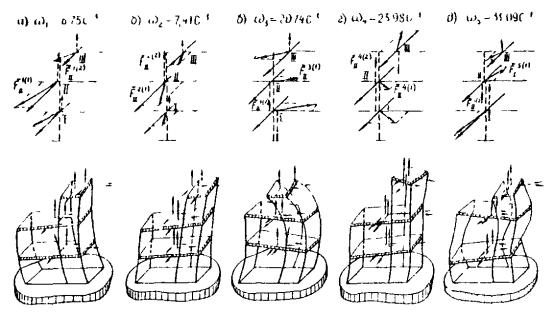
Рис. 7. Схемы движения силосного корпуса в пространстве по первым пяти формам колебаний Данные расчета режима свободных колебаний свидетельствуют о следующем. По первым двум формам преобладают поступательные движения резервуара в горизонтальной плоскости. Для третьей формы характерно в основном вращение относительно вертикальной оси. Для четвертой и пятой форм колебаний в основном имеют место вращения относительно горизонтальных осей. В шестой форме доминируют поступательные вертикальные движения резервуара. Характер движения по первым пяти формам показан на рис. 7. Определение расчетных параметров сейсмического воздействия 12. Согласно п. 2.14 для рассматриваемого примера примем условно расчетную балльность района, равную 8-ми баллам, для которой коэффициент А = 0,2. Для площадки строительства в примере условно примем III категорию грунтов по СНиП II-7-81. По рис. 6 рассматриваемое сооружение имеет размеры в плане 4×4 м, т.е. В = 4 м. Для III категории грунтов при В = 4 м < 25 м по (11) или рис. 2 имеем χ1(4) = 1. По (10) для районов 8-ми балльной зоны III категории грунтов, при В = 4 м имеем следующее значение инварианта ускорения поступательного движения сейсмического воздействия: I(4) = 10 · 0,2 · 1 = 2 м/с2. По п. 2.15 для принятой III категории грунта площадка строительства имеет: Для В = 4 м < 25 м и III категории грунтов по (13) или графикам рис. 3 имеем: χ2(4) = 1. По (12) для III категории грунтов при В = 4 м имеем следующее значение инварианта относительной интенсивности углового ускорения вращения сейсмического воздействия: I(4) = 9 · 10-2 · 1 = 9 · 10-2 (м-1). 14. По п. 2.16 для III категории грунтов по данным табл. 8 имеем: kгр = 0,7. Сооружение выполнено из железобетонных конструкций, т.е. γ = 0,1. По данным табл. 9-10 имеем: uj = bj = 3. Значения периодов собственных колебаний даны в табл. 21. Значения
нормированных коэффициентов значимости ускорения поступательного движения для III категории грунта Таблица 23 Значения коэффициентов динамичности векторов сейсмического воздействия Таблица 24 Значения направляющих косинусов векторов сейсмического воздействия Значения
нормированных коэффициентов динамичности углового ускорения Ненормированные значения коэффициентов динамичности вычисляются по (14) и (18) при kгр = 0,7 и aj = bj = 3. Эти значения коэффициентов динамичности так же даны в табл. 23. 15. По п. 2.17 в качестве проверочных значений примем следующие группы направляющих косинусов векторов сейсмического воздействия. 1. Вектор
2. Вектор
3. Вектор
4. Вектор
Основные расчетные значения направляющих косинусов вычисляются по формулам (22), (23) по заданным значениям коэффициентов форм колебаний, приведенным в табл. 21. Эти значения направляющих косинусов сведены в табл. 24. Расчет режима вынужденных колебаний 16. По п. 2.18 для всех групп значений направляющих косинусов по табл. 24 и всех форм колебаний по табл. 21 по (24) определяются коэффициенты динамичности отдельных форм β(i)j, значения которых сведены в табл. 25. Таблица 25 Коэффициенты динамичности отдельных форм колебаний Таблица 26 Значения сейсмических сил и моментов
Таблица 27 Значения внутренних усилий в нижнем сечении колонны
Таблица 28 Расчетные значения внутренних усилий в нижнем сечении колонны
17. Расчет упругой системы выполнялся по методу сил для формирования матрицы податливости (см. табл. 19) и внутренние усилия в нижнем сечении колонны определялись от единичных сил и моментов (см. табл. 18). Поэтому согласно п. 2.19 основными расчетными параметрами являются векторы сейсмических сил и моментов, значения которых вычисляются по (25). Рассматриваемое сооружение не относится к категории особо ответственных, допуская в нем образование пластических деформаций, примем k = 0,25. Значения векторов сейсмических сил и моментов для всех вариантов ориентации векторов воздействия и для всех форм колебаний сведены в табл. 26. Определение расчетных значений внутренних усилий в поперечном сечении колонны силосного корпуса 20. Согласно п. 2.21 по (27) на основании данных п. 6 и п. 17 выполняется корректировка единичных внутренних усилий (см. табл. 18) на фактические величины сейсмических сил и моментов, значения которых даны в табл. 26. Результаты этой корректировки сведены в табл. 27. 22. Согласно п. 2.23 (29) и данным табл. 27 для каждого варианта ориентации векторов сейсмического воздействия определяются расчетные значения внутренних усилий, значения которых сведены в табл. 28. 23. По п. 2.24 из расчетных значений внутренних усилий, соответствующих различным вариантам ориентации векторов сейсмического воздействия, выбираются максимальные значения, по которым, в сочетании с усилиями от других нагрузок, проверяется прочность колонны. Соответствующие этим максимальным усилиям направляющие косинусы (табл. 29) определяют «опасную» ориентацию векторов сейсмического воздействия. Таблица 29 Значения направляющих косинусов опасной ориентации векторов сейсмического воздействия для нижнего сечения колонны Приложение 2ПРИМЕР РАСЧЕТА СЕЙСМИЧЕСКОЙ НАГРУЗКИ НА КОЛОННЫ И ДИАФРАГМЫ ЖЕСТКОСТИ ТРЕХЭТАЖНОГО КАРКАСНОГО ЗДАНИЯВ качестве примера рассматривается трехэтажное каркасное здание с диафрагмами жесткости, конструктивная схема которого показана на рис. 8.
Рис. 8. Конструктивная схема (а) и расчетная динамическая модель (б) трехэтажного каркасного здания с диафрагмами жесткости В правой части здания расположена лестничная клетка, стены которой являются диафрагмами жесткости. В примере требуется определить сейсмическую нагрузку на колонны каркаса и на диафрагмы жесткости для рассматриваемого здания. Описание расчетной динамической модели здания Согласно п. 2.2 расчетную динамическую модель принимаем в виде трех твердых пластин, соединенных между собой и с основанием стержневыми и пластинчатыми упругими элементами, как показано на рис. 8. По п. 2.3 каждый диск расчетной динамической модели имеет три системы свободы и совершает плоскопараллельные колебания в горизонтальной плоскости. Всего система имеет 3×3 = 9 степеней свободы. Инерционные параметры масс равны: мI = 0,651×106 кг; мII = 0,666×106 кг; мIII = 0,186×106 кг; θ3I = 0,1612×109 кг · м2; θ3II = 0,1582×109 кг · м2; θ3III = 0,6222×107 кг · м2 По п. 2.4 железобетонные колонны каркаса моделируем стержневыми элементами, а конструктивные элементы лестничной клетки - упругими пластинами с геометрическими характеристиками их распределения в соответствии с рис. 8. Описание геометрических параметров динамической модели выполняется согласно п. 2.5: - инерциальные оси отсчета ОX1Х2X3 принимаем параллельными осям Оx01x02x03, (cм. рис. 8); - начало осей ОХ1X2X3 связываем с геометрическим центром фундамента в плане; - [φ0] = Е - единичная матрица; - устанавливаем нумерацию дисков перекрытий снизу вверх, I, II, III (см. рис. 8); - с каждым диском связываются системы отсчета КХК1XК2ХК3 (К = I, II, III) (см. рис. 8). Эти оси являются главными и центральными осями инерции дисков; - все оси КХК1XК2ХК3 параллельны осям Ox01x02x03, см. рис. 8. Поэтому [φk] = Е - единичная матрица; - векторы Единичные внутренние усилия в нижнем сечении колонны К-2 на уровне первого этажа
Таблица 31 Единичные погонные внутренние усилия в пластинчатом элементе П-1 на уровне первого этажа
Таблица 32 Матрица податливости Таблица 33 Матрица инерционных параметров Описание упругих свойств расчетной динамической модели По п. 2.6 для статического расчета упругой системы применим программы расчета, основанные на методе конечных элементов. Согласно п. 2.7 от последовательного действия единичных сил и моментов выполняем статический расчет и определяем внутренние усилия в узлах упругих элементов, а также определяем перемещения и углы поворотов дисков. В качестве примера в табл. 30 приведены внутренние усилия в нижнем сечении колонны К-2 в уровне 1 этажа, а в табл. 31 даны расчетные внутренние усилия для пластины П-1 (см. рис. 10). Матрица податливости приведена в табл. 32. Расчет режима свободных колебаний Согласно п. 2.6 анализ матрицы [δ] показывает, что она не содержит обособленных составляющих. Согласно п. 2.10 матрица инерционных параметров рассматриваемой системы приведена в табл. 33. Матрица [В] = [δ][М] так же не содержит обособленных составляющих. По п. 2.11 задача по определению частот и форм собственных колебаний решается по полной матрице [В]. Результаты решений сведены в табл. 34. По п. 2.12 полученные коэффициенты форм колебаний нормированы на значения Z(j)x1I (j = 1 ÷ 9), которые приняты за единицу, см. табл. 34. Согласно п. 2.13 результаты проверки условий ортогональности найденных форм колебаний сведены в табл. 35. На рис. 9 показаны схемы движения масс дисков перекрытий и покрытия, а также ориентация векторов коэффициентов по первым пяти формам колебаний. Таблица 34 Значения параметров форм колебаний
Рис. 9. Схема движения дисков перекрытий трехэтажного каркасного здания по первым пяти формам колебаний Определение расчетных параметров сейсмического воздействия По п. 2.14 примем расчетную балльность равной 8-ми баллам, для которой, согласно СНиП II-7-81, А = 0,2. Для площадки строительства примем грунты III категории по СНиП II-7-81. По данным рис. 8 здание имеет размеры в плане 12×52 м, т.е. для расчета В = 12 м. По (11) или графикам рис. 2 для III категории грунтов при В = 12 м < 25 м имеем χ1(12) = 1. По (10) значение инварианта интенсивности ускорения поступательного движения грунта равно: I(12) = 10 × 0,2 × 1 = 2 м/с2. По п. 2.15 для III категории грунтов - По (13) или графикам рис. 3 для III категории грунтов при В = 12 м имеем χ2(12) = 1. По (12) имеем: W(12) = 9 × 10-2 × 1 = 9 × 10-2 (м-1). Таблица 35 Условия ортогональности форм колебаний
По п. 2.16 для III категории грунтов по табл. 8 kгр = 0,7. Сооружение выполнено из железобетонных конструкций, при колебаниях которых коэффициент потерь энергии равен 0,1. Для γ = 0,1 по табл. 9 и 10 αγ = bγ = 3. Значения
нормативных коэффициентов динамичности ускорения поступательного движения
сейсмического воздействия для III категории
грунтов определяется по (17) или графикам
рис. 4 в зависимости от периодов
собственных колебаний (см. табл. 34).
Для рассматриваемого примера Значения
нормативных коэффициентов динамичности углового ускорения вращения
сейсмического воздействия вычисляются по (19)
или по рис. 5. Для заданных периодов
собственных колебаний Ненормированные
значения Согласно п. 2.17 в качестве проверенных значений
направляющих косинусов примем их группу,
соответствующую ориентации 1. 2. 3. 4. 5. 6. i = 1, 2, 3. Группа основных расчетных значений направляющих косинусов определена по (20)-(23) и для заданных значений коэффициентов форм колебаний (см. табл. 34) сведена в табл. 37. Таблица 36 Значения коэффициентов динамичности векторов сейсмического воздействия Расчет режима вынужденных колебаний По п. 2.18 значения коэффициентов динамичности β(i)j для всех форм и вариантов ориентации векторов сейсмического воздействия определены по (24) и сведены в табл. 38. В табл. 39 даны отношения β(i)j / β(1)j (i = 1 ÷ 15; j = 1 ÷ 9). Расчет упругой системы выполнялся по методу сил. Внутренние усилия в проверяемых элементах К-2 и П-1 определялись от единичных сил и моментов (см. табл. 30-31). Поэтому в соответствии с п. 2.19 основными расчетными параметрами являются величины сейсмических сил и моментов, значения которых определяются по (25). Поскольку рассматриваемое сооружение не относится к особо ответственным, допуская в нем образования пластических деформаций, примем k = 0,25. Величины сейсмических сил и моментов, вычисленные по (25) для
первого варианта ориентации векторов сейсмического воздействия и всех форм колебаний,
сведены в табл. 40. Для всех остальных вариантов Определение расчетных значений внутренних усилий в нижних сечениях колонны К-2 и панели П-1 Согласно п. 2.21 по (27) выполняется корректировка
единичных внутренних усилий, приведенных в табл. 30 и 31 на фактические
величины сейсмических сил и моментов, значения которых даны
в табл. 40. Результаты вычислений для первого
варианта ориентации Согласно п. 2.23 по (29) с использованием данных табл. 39 и табл. 41 и 42 для каждого варианта ориентации векторов сейсмического воздействия определяются расчетные значения внутренних усилий, величины которых сведены в табл. 43 и 44 для рассматриваемых сечений колонны К-2 и панели П-1. Таблица 37 Значения направляющих косинусов векторов сейсмического воздействия Таблица 38 Значения коэффициентов динамичности отдельных форм колебаний β(i)j Таблица 39 Таблица отношений коэффициентов β(i)j / β(1)j
Таблица 40 Значения сейсмических сил и моментов
Таблица 41 Значения внутренних усилий в нижнем сечении колонны К-2 на уровне первого этажа
Таблица 42 Значения погонных внутренних усилий в пластинчатом элементе П-1 на уровне первого этажа
Таблица 43 Расчетные значения внутренних усилий в нижнем сечении колонны К-2 на уровне первого этажа Таблица 44 Расчетные значения погонных внутренних усилий в пластинчатом элементе П-1 на уровне первого этажа Согласно п. 2.24 из табл. 43 и 44, в качестве расчетных значений для проверки прочности в сочетании с усилиями от других видов нагрузок, выбираются максимальные величины, соответствующие одному варианту ориентации векторов воздействия. Значения направляющих косинусов «опасной» ориентации векторов сейсмического воздействия для нижних сечений колонны К-2 и панели П-1 даны в табл. 45. Таблица 45 Значения направляющих косинусов опасной ориентации векторов сейсмического воздействия
Приложение 3ОСНОВНЫЕ ПОЛОЖЕНИЯ ПО ОПРЕДЕЛЕНИЮ СЕЙСМИЧЕСКОЙ НАГРУЗКИ С УЧЕТОМ ПРОСТРАНСТВЕННОГО ХАРАКТЕРА ВОЗДЕЙСТВИЯ И РАБОТЫ КОНСТРУКЦИЙ СООРУЖЕНИЯРасчетные динамические модели сооружений и их параметрыДля выполнения расчетов требуется сформировать расчетные модели сооружения и сейсмического воздействия. Вопросы формирования расчетных динамических моделей сооружений рассмотрены в работах [8, 14, 15]. В настоящих Рекомендациях в основу расчетов приняты дискретные динамические модели, движение масс которых описывается обыкновенными линейными дифференциальными уравнениями. Дискретная расчетная динамическая модель сооружения формируется в соответствии с соотношением жесткостей отдельных конструкций. Наиболее жесткие конструкции сооружения принимаются в виде отдельных масс (абсолютно твердых тел). Конструкции, жесткость которых на порядок ниже, считаются невесомыми упругими связями, соединяющими дискретные абсолютно твердые массы. Вопрос о том, какие конструкции в расчетах считать абсолютно твердыми и недеформируемыми, а какие конструкции принимать упругими безинерционными является неоднозначным. По оценке деформации сооружения в целом и влиянию на ее величину и характер отдельных составляющих, можно судить о соотношении жесткостей отдельных конструкций сооружений. Так, например, если искривления перекрытий зданий в своей плоскости незначительны и вклад этих деформаций в общие горизонтальные перемещения сооружения по уровням отдельных этажей мал, то эти перекрытия можно считать абсолютно твердыми телами (массами), соединенными между собой упругими вертикальными несущими конструкциями каркаса. Другим фактором, поясняющим проблему выбора расчетной динамической модели сооружения, является следующее обстоятельство. Если в расчетной модели какая-то часть сооружения принимается абсолютно твердой, то она в расчетах считается недеформируемой и в ней невозможно определить внутренние усилия. Следовательно, если в расчетах отсутствует необходимость проверять прочность какого-то элемента и, очевидно, что жесткость его довольно высокая в сравнении с другими конструкциями, то в расчетной модели этот элемент целесообразно принять за абсолютно твердую массу, Дополнительным фактором, поясняющим выбор расчетной динамической модели сооружения, является то обстоятельство, что динамические расчеты, к каким относятся расчеты на сейсмические воздействия, базируются на статических расчетах сооружения, при которых выполняется построение матрицы жесткости или податливости сооружения в целом. Расчетные статическая и динамическая модели сооружения могут отличаться друг от друга. Расчетная статическая модель сооружения может быть более подробной. В ней все элементы могут приниматься деформируемыми. При переходе к расчетной динамической модели сооружения ряд деформируемых элементов может объединяться в группу в виде твердой массы. Перемещения или углы вращения этой массы в виде соответствующих компонент матриц жесткости или податливости будут уже определяться с учетом деформативных свойств элементов, представляющих в динамической модели эти твердые массы. Такое укрупнение часто применяется в расчетах, основанных на методе конечного элемента. Сооружение детально разбивается на конечные элементы. С учетом подробного анализа деформативных свойств определяются необходимые перемещения и углы поворотов (вращений), из которых далее компонуется матрица жесткости или податливости сравнительно малого порядка. Этот прием получил широкое распространение во многих автоматизированных системах расчета, но он требует определенной осторожности, связанной со спецификой динамического расчета, рассматриваемого в настоящих Рекомендациях. Приведем пример, поясняющий этот прием. Предположим, что возник вопрос, связанный с учетом деформаций перекрытий зданий в своей плоскости. Тогда эти перекрытия могут быть разбиты на конечные элементы. С учетом податливости перекрытий определены перемещения центров масс и углы вращения относительно вертикальных осей, проходящих через эти центры масс. Из этих перемещений и углов вращения в соответствии с приведенными ниже требованиями формируется матрица податливости сооружения. В динамическом расчете эти перекрытия можно считать абсолютно твердыми дисками с учетом геометрических параметров распределения масс. При рассмотрении динамики такой системы эти диски перекрытий будут совершать плоскопараллельное движение в горизонтальной плоскости, но уже с учетом податливости самих перекрытий. Аналогично можно поступить с любым другим элементом сооружения. Приведенные здесь данные поясняют характер п. 2.2 алгоритма расчета. Подпункт о необходимости моделирования фундамента сооружения твердым телом относится к специфике учета пространственного характера сейсмического воздействия (см. п. 2.14-2.17 и пояснения к ним). После выделения в сооружении условно недеформируемых (абсолютно жестких) элементов, несущих массу, и податливых, моделирующих упругие связи, возникает вопрос: каким образом представить массу жестких элементов? В механике известны три модели представления материального объекта: материальная точка, твердый диск и твердое тело. На базе динамики каждой из этих моделей может быть описана динамика сооружения, как пространственной системы. В соответствии с критериями формирования расчетных динамических моделей [8, 9, 14, 15], они подразделяются на одно-, двух- и трехмерные, в зависимости от траекторий движения точек масс модели. Если траектории движения точек массы представляют параллельные прямые линии (движение по оси), то такие расчетные динамические модели являются одномерными [1, 13, 15, 16]. Если траектории движения точек расположены в параллельных плоскостях (движение по двум осям), то расчетные динамические модели называются двухмерными. В случае, когда криволинейные траектории движения точек являются пространственными кривыми (движение по трем осям), расчетные динамические модели называются трехмерными. Согласно установившейся терминологии, в теории сейсмостойкости сооружений под пространственными понимаются двух- и трехмерные расчетные динамические модели. Пространственная расчетная динамическая модель может быть представлена системой материальных точек, дисков и тел или комбинацией этих элементов. При этом необходимо иметь в виду, что учет геометрических характеристик распределения массы в жестких элементах и учет геометрии распределения упругих связей, несущих эти элементы, может быть выполнен только при представлении жесткого элемента в виде твердого тела или его частного случая - твердого диска (см. пп. 2.3-2.4). Моделировать твердым диском жесткий элемент следует в том случае, если описывается плоскопараллельное движение рассматриваемого элемента. При этом рассматриваемый элемент должен иметь размеры, развитые в плоскости движения. Типичным примером такого случая является плоскопараллельное движение дисков перекрытий в своей плоскости. Если перекрытие принято за недеформируемый элемент, то его можно моделировать твердым диском. Диск отличается от тела тем, что он имеет два линейных размера, тогда как у тела их три. Твердый диск имеет три степени свободы (два поступательных перемещения его центра масс и угол поворота относительно оси, перпендикулярной плоскости диска и проходящей через его центр масс). Все точки диска при его плоскопараллельном движении описывают траектории, лежащие в плоскости диска. Расчетные динамические модели сооружения с твердыми дисками являются двухмерными [9, 10, 15] и относятся к одному из частных случаев пространственных систем. Поскольку диск имеет два линейных размера, то он позволяет учесть геометрические параметры распределения массы по диску, а также представляет возможность учесть геометрические параметры распределения в плоскости диска упругих связей, несущих диск. Инерционные параметры диска определяются величиной массы m, которая вычисляется в соответствии с требованиями п. 2.2 СНиП II-7-81 и моментом инерции массы θ относительно оси, перпендикулярной плоскости диска и проходящей через центр его масс. Координаты центра масс диска и его момент инерции следует вычислять, используя справочные данные [5, 16]. Если принятый жесткий элемент имеет один порядок всех трех линейных размеров, то такой элемент следует моделировать твердым телом. Твердое тело, имеющее все необходимые размеры, допускает учет геометрических параметров распределения массы и несущих упругих связей в пространстве. Свободное твердое тело имеет шесть степеней свободы: три перемещения центра масс и три угла вращения относительно осей, проходящих через центр масс. В общем случае траектории движения точек тела представляют кривые, определенные в пространстве. Инерционные параметры твердого тела характеризуются величиной массы m, определяемой с учетом требований п. 2.1 СНиП II-7-81 и тензором инерции [5], который представляет матрицу моментов инерции массы где θij (i, j = 1, 2, 3) - осевые (при i = j) и центробежные (при i ≠ j) моменты инерции массы тела относительно некоторых осей. В главных и центральных осях инерции тела центробежные моменты инерции равны нулю и тензор (30) принимает вид диагональной матрицы
В последнем случае требуется вычислять только три момента инерции массы тела. Положение центра масс, ориентация в пространстве главных и центральных осей и осевые моменты инерции θi (i = 1, 2, 3) определяются по справочным данным [5, 16 и др.]. Рассматриваемые алгоритмы расчета построены таким образом, что всегда необходимо в качестве осей отсчета принимать только главные и центральные оси инерции тел. В рассматриваемых алгоритмах согласно п. 2.3 допускается применять в расчетных динамических моделях любой вид масс, с учетом приведенных выше данных. При этом расчетные динамические модели должны быть как минимум двухмерными. Рассматриваемые алгоритмы расчета линейных пространственных колебаний сооружений основаны на решениях обыкновенных линейных дифференциальных уравнений, в предположении линейной работы материала несущих конструкций, что отмечается в п. 2.4. Модели несущих конструкций принимаются в виде упругих стержней различного типа, пластин и др. Выбор этих моделей определяется принятыми массами в динамической модели и требованиями статического расчета упругой системы при формировании матриц жесткости или податливости. Дальнейшее определение расчетной динамической модели сводится к описанию ее геометрических параметров по изложенному в п. 2.5 алгоритму расчета. Поскольку вектор ускорения поступательного движения грунта определяется в инерциальных осях ОХ1X2Х3, то такая система должна быть введена в соответствии с требованиями п. 2.5. Вектор углового ускорения
вращения сейсмического воздействия определяется в осях Ox01x02x03, неизменно
связанных с основанием (фундаментом), которые вводятся в расчетную динамическую модель согласно
требований п. 2.5. Аналогично, по п.
2.5 с
каждой из масс расчетной динамической модели связывается своя система осей kxk1xk2xk3,
(k = I, II, III, ..., n - номера
масс, присваиваемые согласно п. 2.5). Если k-ая масса представлена в виде твердого тела (диска), то kxk1xk2xk3 должны быть
главными и центральными осями инерции этой массы. Таким образом, реальная
динамическая модель на стадии описания ее геометрических параметров заменяется
совокупностью систем осей, как показано на рис. 10, и задача сводится к описанию взаимного
расположения этих осей в пространстве. Взаимное положение
осей в пространстве определяется координатами их начал отсчета и относительной
ориентацией в пространстве. Начало всех систем осей kxk1xk2xk3,
(k = I, II, III, ..., n), связанных с
массами сооружения, определяются в осях Ox01x02x03 векторами Рис. 10. Система осей, вводимая в расчетную динамическую модель ОХ1X2X3 - инерциальная система отсчета; Ox01x02x03 - система осей, связанная с основанием; kxk1xk2xk3 - система осей, связанная с k-й (k = I, II, III, ..., n) массой Относительная ориентация осей определяется операторами взаимосвязи между их ортами (единичными векторами). Применительно к определению пространственной ориентации осей Oy1y2y3 относительно осей Ox1x2x3 (рис. 11) такой оператор имеет вид следующей матрицы: где φik (i, k = 1, 2, 3) - скалярные произведения единичных векторов jyi и jxk (орты осей Oy1y2y3 и Ox1x2x3, соответственно); точкой отмечен знак скалярного произведения.
Рис. 11. Схемы поворотов системы осей Оy1y2y3 относительно осей Ox1x2x3 а - поворот относительно оси Оx1 на угол α1; б - поворот относительно оси Оx2 на угол α2; в - поворот относительно оси Ox3 на угол α3; г - последовательные повороты на углы α1, α2, α3 (карданова система углов) Скалярные произведения φik (компоненты матрицы (32)) представляют проекцию единичного вектора jxk на направление вектора jyi, т.е. где На рис. 11 приведены схемы, поясняющие вычисления компонент матрицы (33) при различных вращениях осей. На схемах рис. 11, а-в показаны повороты системы осей относительно первой, второй и третьей осей на углы α1, α2 и α3, соответственно. При повороте на угол α1 относительно оси Оx1 матрицы (32) имеют следующий вид: При повороте на угол α2 относительно оси Ox2 (см. рис. 11, б) матрица (32) имеет следующие компоненты: При повороте на угол α3 относительно оси Ox3 (см. рис. 11, в) - (32) имеет значения: На рис. 11, г показана схема трех последовательных поворотов осей Oy1y2y3 относительно осей Ox1x2x3. В этом случае от орт осей системы Ox1x2x3 к ортам осей Oy1y2y3′ переход выполняется последовательным произведением матриц (34)-(36) Аналогично матрица [φ] вычисляется при двух любых последовательных поворотах. На практике часто встречаются оси, повернутые друг относительно друга только по вертикальной оси. Как правило, таковы оси инерциальной системы отсчета ОХ1X2Х3 и главные оси сооружения, связанные с основанием Ox01x02x03, см. п. 2.5. Поэтому матрица [φ0] (1) практически всегда определяется в виде (36). Для большинства сооружений главные центральные оси инерции масс расчетных динамических моделей так же имеют вертикально ориентированную третью ось, т.е. в большинстве случаев матрицы [φk] (2) (см. п. 2.5) также вычисляются по (36). Однако, если сооружение несет большие сконцентрированные массы, то их главные центральные оси инерции могут быть ориентированы в пространстве различным образом. В этих случаях при определении [φk] (2) по п. 2.5 необходимо исходить из данных (34), (35), (36) и схемы (37). Можно также применять результаты непосредственных углов между осями и вычислять компоненты [φk] (2) по (35). Всегда необходимо иметь в виду, что компоненты этих матриц должны удовлетворять следующим условиям нормирования:
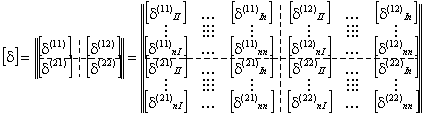
Первое условие определяет единичную величину модуля орт осей Oy1y2y3 и второе - ортогональность этих орт. Необходимо также иметь в виду, что если рассматриваемые оси одинаково ориентированы в пространстве, то (32) принимает вид единичной матрицы, которую можно получить по (34)-(37) при нулевых значениях соответствующих углов α. Описание упругих свойств расчетной динамической модели сооруженияЖесткости сооружений определяются статическими расчетами, которые выполняются по соответствующим статическим моделям сооружений. Для определения сейсмической нагрузки на сооружение необходимо знать его динамические параметры: спектр собственных частот и параметры диссипации. Статическая и динамическая модели сооружений могут отличаться друг от друга. Статическая модель сооружения может быть более подробной, чем динамическая. Однозначное соответствие статической и динамической моделей состоит только в том, что статическая модель должна допускать возможность определения жесткостей по соответствующим направлениям движения масс в принятой динамической модели. Имеется ряд методов статических расчетов сооружений [1, 2, 16 и др.]: методы сил и перемещений; метод конечных элементов и конечных разностей и т.д. На основе этих методов разработаны системы автоматизированных статических расчетов сооружений на ЭВМ, которые в данной работе не рассматриваются. Здесь приводятся отдельные сведения статического расчета, которые необходимы для выполнения динамического расчета сооружения на сейсмические воздействия. Формулируется требуемый вид окончательных результатов и поясняется их физический смысл. Для получения этих данных можно использовать любые методы, алгоритмы и программы статического расчета упругих систем на ЭВМ, как отмечается в п. 2.6 данных Рекомендаций. При выполнении этих расчетов ставятся две задачи. 1. По принятой статической модели сформировать матрицу жесткости [r] или податливости (перемещений) [δ], определяя компоненты этих матриц в точках сосредоточения масс динамической модели. 2. Для элементов конструкций, прочность которых проверяется на сейсмическое воздействие, определить напряженно-деформированное состояние от единичных воздействий. В зависимости от применяемого метода расчета единичными могут быть либо единичные силы и моменты, либо единичные перемещения и углы вращения. В п. 2.7 алгоритма расчета приведены необходимые пояснения для статического расчета по методу сил, когда внешним воздействием являются единичные силы рxik = 1 и моменты Mxik = 1, где i = 1, 2, 3; k = I, II, ..., III - номера масс расчетной динамической модели сооружения. Единичные силы Рхik = 1 прикладываются к статической модели в точке, соответствующей центру масс твердого диска или тела в динамической модели. Причем силы Рхik = 1 прикладываются по направлению осей, связанных с основанием сооружения Ox01x02x03. Единичные моменты Mxik = 1 прикладываются относительно главных центральных осей инерции масс kxk1xk2xk3. Последовательно, отдельно от действия каждой единичной силы (или момента), как от внешней нагрузки, выполняется расчет статической модели сооружения. Этот расчет может быть выполнен с привлечением любых, имеющихся в распоряжении расчетчика, программ, вычислительных комплексов и т.д. Рассмотрение специфики такого расчета является предметом других инструктивных документов и здесь не развивается. В результате этого расчета должны быть отдельно от каждой из единичных сил Рxik = 1 (или моментов Mxik = 1) определены: - напряженно-деформированное состояние всех элементов, прочность которых проверяется на сейсмическое воздействие, результаты сводятся в таблицы типа табл. 1; по этим результатам, после определения сейсмических сил и моментов, путем корректировки их на фактические величины сил и моментов, вычисляются расчетные параметры напряженно-деформированного состояния; каждое единичное загружение силой или моментом определяет свое напряженно-деформированное состояние рассматриваемых элементов; - вычисляются перемещения всех точек статической модели сооружения, соответствующих центрам масс динамической модели; перемещения вычисляются по направлениям осей, связанных с основанием сооружения; вычисляются также величины углов поворотов (вращения) масс динамической модели относительно главных центральных осей инерции этих масс; фактически определяются углы поворота осей, введенных в статическую модель, поскольку эти оси неизменно связаны с массами динамической модели, то углы поворота осей статической модели соответствуют углам поворота масс динамической модели; из этих перемещений и углов вращения формируется матрица податливости динамической модели [δ] и далее в расчете рассматривается только динамическая модель. Матрица [δ] формируется в виде табл. 2. Каждое единичное загружение (Рxik = 1 или Mxik = 1; i = 1, 2, 3; k = I, II, III, ..., n) определяет свой столбец матрицы [δ]. Полная совокупность загружений определяет число столбцов, соответствующих числу строк, и матрица [δ] имеет квадратный симметричный вид со следующей структурой: где [δ(st)кр] (k, р = I, II, ..., n; s, t = 1, 2) - составляющие матрицы размером 3×3 в виде: δ(st)крij (i, j = 1, 2, 3) - при S = 1 перемещения начала k-ой системы отсчета по направлению ее i-ой оси системы Ox01x02x03 (при S = 2 углы поворота k-ой системы отсчета относительно k-ой оси системы kxk1xk2xk3) от действия при t = 1 единичной силы, приложенной к началу р-ой системы отсчета по направлению j-ой системы Ox01x02x03 (при t = 2 от единичного момента, приложенного относительно j-ой оси p-ой системы отсчета Pxp1xp2xp3). Здесь записана матрица податливости системы для случая, когда каждая из n масс расчетной динамической модели представлена в виде твердого тела с шестью степенями свободы. Количество степеней свободы такой динамической модели равно 6n и оно определяет: - число единичных загружений для статической модели; - число напряженно-деформированных состояний для всех элементов, прочность которых проверяется на сейсмическое воздействие (см. табл. 1); - число строк и столбцов матрицы податливости [δ] - ее порядок. Если в расчетной
динамической модели часть масс представлена материальными
точками, а другая часть - твердыми дисками или
телами, то число степеней свободы такой модели равно Рассмотрим структуру блочной матрицы податливости [δ] (40). Она соответствует следующему блочному вектору параметров движения масс расчетной динамической модели: где xik и αik (i = 1, 2, 3) - перемещения и углы поворота k-ой массы. Определяются матрицы (40) и вектор (42) от отдельного действия каждой из компонент следующего блочного вектора нагрузки: где Pxik и Mαik (i = 1, 2, 3) - единичные силы и моменты. Структура (40), (42) и (43) приведена для случая, когда каждая из масс расчетной динамической модели имеет шесть степеней свободы и представлена твердым телом. Если в расчетной динамической модели какая-то масса имеет меньше шести степеней свободы и представлена материальной точкой или твердым диском, то из (42) и (43) следует исключить компоненты, соответствующие отсутствующим степеням свободы, удалив при этом из матрицы (40) соответствующие строки и столбцы. Структура матрицы податливости (40) и векторов (42), (43) в целом при этом сохраняется. Принятая здесь блочная структура векторов и матриц подчеркивает пространственный характер движения масс сооружения при расчете на сейсмические воздействия. Блок [δ(11)] (40) соответствует описанию поступательного движения точечных масс или центров масс дисков и тел. Блок [δ(21)] соответствует описанию вращения дисков или тел относительно своих центров масс. Блоки второстепенной диагонали [δ(12)] = [(δ(21))′] (где ′ (штрих) - знак транспонирования) соответствуют описанию взаимосвязи поступательного движения и вращения. Если блоки второстепенной диагонали являются нулевыми матрицами, то поступательные и вращательные движения масс не взаимосвязаны и проходят самостоятельно. Таким образом, сама деформационная структура сооружения (его статической и динамической моделей) определяет через [δ] (40) тот или иной пространственный характер движения масс. В режиме вынужденных колебаний этот характер усложняется за счет пространственных моделей сейсмического воздействия. Описанные положения статического расчета упругой модели сооружения методом сил приводят к обратной форме задачи динамики сооружений. К прямой форме этих задач приводит статический расчет по методу деформаций, когда формируется матрица жесткости [r] для расчетной динамической модели. В данном случае, в отличие от требований п. 2.7, вычисляются не перемещения и углы вращения, а определяются соответствующие им обратные величины - жесткости. Для этой цели в статической модели сооружения, в точках, соответствующих центрам масс, накладываются три ортогональные связи, препятствующие линейным перемещениям в трех ортогональных направлениях осей, связанных с основанием Ox01x02x03. Накладываются также угловые связи, препятствующие углам поворотов относительно главных центральных осей инерции масс. Последовательно каждой из наложенных связей сообщается соответствующее единичное перемещение (единичный угол поворота) и определяются: - напряженно-деформированное состояние всех элементов, прочность которых проверяется на сейсмическое воздействие. Результаты этого расчета сводятся в таблицы вида табл. 3. По этим результатам, после определения сейсмических перемещений и углов вращения масс, путем корректировки на фактические величины вычисляются расчетные параметры напряженно-деформированного состояния. Каждое единичное перемещение (угол поворота) определяет свое напряженно-деформированное состояние рассматриваемых элементов; - вычисляются реакции во всех наложенных на систему связях. Из этих реакций (сил и моментов) формируется матрица жесткости динамической модели [r] и далее в расчетах рассматривается динамическая модель. Матрица [r] формируется в виде табл. 4. Каждое единичное перемещение (угол поворота) определяет свой столбец матрицы [r]. Полная совокупность перемещений и углов поворотов определяет число столбцов, равное числу строк, и матрица [r] имеет квадратный симметричный вид: где [r(st)kp] (k, p = I, II, ..., n; s, t = 1, 2) - составляющие матрицы размером 3×3
r(st)kpij (i, j = 1, 2, 3) - при s = 1 силы реакции линейной связи, наложенной на начало k-ой системы отсчета по направлению i-ой оси системы Ox01x02x03 (при S = 2 моменты реакции угловой связи, наложенной относительно i-ой системы kxk1xk2xk3) от единичного перемещения при t = 1 линейной связи, наложенной на начало р-ой системы отсчета по направлению p-ой оси системы Оx01x02x03 (единичного угла поворота при t = 2 угловой связи, приложенной относительно j-ой оси системы pxp1xp2xp3). Матрица жесткости системы (44) записана для случая, когда каждая из n масс расчетной динамической модели представлена твердым телом с шестью степенями свободы. Количество степеней свободы такой динамической модели равно 6n и в данном случае определяет: - число накладываемых на систему связей и число единичных перемещений и углов поворота; - число напряженно-деформированных состояний для всех элементов, прочность которых проверяется на сейсмическое воздействие (см. табл. 3); - число строк и столбцов матрицы жесткости [r] (44) - ее порядок. В случаях, когда
в расчетной динамической модели часть масс представлена
материальными точками, а другая часть - твердыми дисками и телами, число степеней свободы равно Блочная структура матрицы жесткости [r] (44) соответствует определению блочного вектора реакций (43) по блочному вектору перемещений (42), т.е. в данном случае решается обратная задача, в отличие от п. 2.7 рассматриваемого алгоритма. Если в расчетной динамической модели какая-то масса имеет число степеней свободы меньше шести и представлена в виде точки или диска, то из (43) и (42) следует исключить соответствующие строки и столбцы. При этом структура (42), (43), (44) сохраняется. Принятая блочная структура матрицы жесткости системы соответствует описанию пространственного характера движения масс сооружения. Блок [r(11)] (44) соответствует описанию поступательного движения точечных масс или центров масс дисков и тел. Блок [r(22)] соответствует описанию вращения дисков или тел относительно своих центров масс. Блоки второстепенной диагонали [r(21)] = [r(12)′] соответствуют описанию взаимосвязи поступательного и вращательного движений. При нулевых блоках второстепенной диагонали матрицы податливости или жесткости поступательные и вращательные движения масс сооружения не взаимосвязаны и образуют самостоятельные группы колебаний. Расчет режима свободных колебанийРасчет режима свободных колебаний рассматриваемых динамических моделей сооружения выполняется по п.п. 2.9-2.13. Пространственный характер движения масс сооружения зависит от его деформационных свойств, которые определены матрицей податливости [δ] (40) или жесткости [r] (44), вычисляемыми по статической модели. Между матрицами [r] и [δ] существует обратная зависимость, т.е. [r] = [δ-1], (46) где -1 - знак обращения матрицы. Соотношения (46) удовлетворяются для всех матриц, которые не содержат обособленных составляющих. Определение обособленных составляющих матрицы дано в математической литературе [3]. Поясним это определение на примере. Если блоки второстепенных диагоналей матрицы [δ] (40) или [r] (44) являются нулевыми матрицами, то блоки главных диагоналей [δ(ss)] или [r(ss)] (s = 1, 2) являются самостоятельными и независимыми. Каждый из этих блоков определяет свои независимые деформации, соответствующие независимым формам колебаний. В данном случае обратные соотношения выполняются между этими блоками, т.е. [r(ss)] = [(δ(ss))-1], (s = 1, 2). (47) Если система абсолютно симметрична, то составляющие (41) и (46) представляют диагональные матрицы, что приводит к распаданию каждого из блоков главной диагонали [δ(ss)] и [r(ss)] (s = 1, 2) на три независимые составляющие, между которыми также удовлетворяются обратные соотношения в виде (4). В этом случае исходные матрицы [δ] или [r] в виде (40) или (44) распадаются на шесть независимых составляющих, каждая из которых имеет порядок n (если все массы представлены телами). Суммарный порядок задачи остается равным 6n. Каждую из матриц (40) и (44) в данном случае можно представить в виде суммы независимых составляющих (3) по диагонали, т.е. Каждый из диагональных блоков (48) представляет обособленную матрицу, анализ свойств которой всегда следует выполнять отдельно. Поскольку соответствующие строки и столбцы матрицы можно менять местами, то при нулевых компонентах в этих строках и столбцах, матрицу всегда можно привести к виду с обособленными составляющими, расположенными на главной диагонали (48). Другой способ выделения обособленных составляющих состоит в построении системы линейных алгебраических уравнений, коэффициенты которых являются компонентами исходной матрицы. Если при этом одна какая-то группа уравнений не зависит от другой группы уравнений, то коэффициенты этих групп уравнений образуют обособленные составляющие полной матрицы. Путем перегруппировки неизвестных этих уравнений (перестановки местами составляющих строк и столбцов) можно для исходной матрицы достичь вида (48). Для матрицы податливости [δ] (40) или жесткости [r] (44) каждая из обособленных составляющих описывает свою независимую группу деформаций и соответствует самостоятельной группе колебаний. Выделение обособленных составляющих матриц по п. 2.9 алгоритма связано со свойствами асимметрии рассматриваемых упругих систем. Как известно [15], упругие системы могут быть абсолютно симметричными, полностью или частично асимметричными. Частично асимметричные системы в свою очередь делятся на системы с однородной и неоднородной асимметрией. Для полностью асимметричных систем не образуется обособленных составляющих (40) и (44). Для абсолютно симметричных систем эти матрицы распадаются на шесть обособленных составляющих. Для частично асимметричных систем число обособленных составляющих всегда меньше шести, но конкретное число и структура обособленных составляющих для данного типа систем определяется конкретными видами частичной асимметрии. Анализ этих составляющих по видам частичной асимметрии рассмотрен в [9, 15], где по физическому характеру системы определяется структура обособленных составляющих [r] или [δ]. Анализ матриц [r] или [δ] является вспомогательным, он дает представление о физической стороне задачи. Этот анализ является необходимым, но недостаточным, поскольку расчет режима свободных колебаний выполняется по динамическим характеристикам, представляющим комбинацию матриц [r] или [δ] и [М]. Поэтому согласно п. 2.10 алгоритма требуется проанализировать матрицы [А] = [М-1][r] или [В] = [δ][М], (49) где [А] = [В-1]. (50) Здесь [M] диагональная матрица инерционных параметров, структура которой, для случая представления всех масс динамической модели твердыми телами, дана в табл. 5. Если какая-то масса динамической модели представлена материальной точкой или твердым диском, то из структуры табл. 5 необходимо исключить соответствующие параметры. Решение задачи
на определение частот и форм собственных колебаний выполняется по матрице [А] в прямой форме (7)
или по матрице [B]
в обратной форме (8) частотных
уравнений. Задача сводится к определению собственных чисел типа Ω2j для матрицы [А] или
типа 1 / Ω2j для матрицы [В], а также собственных векторов Решение задачи по анализу матриц [А] или [B] на обособленные составляющие выполняется аналогично тому, как было описано выше, для аналогичного анализа [r] или [δ]. Совместный анализ матриц статического состояния [r] или [δ], согласно п. 2.9, и динамических характеристик [А] или [В] по п. 2.10 позволяет понять физическую основу решаемой динамической задачи и корректно сформулировать математическую постановку задачи. Решение задачи на собственные значения матриц [А] или [B] можно выполнить только отдельно для каждой
обособленной составляющей [Аi] или [Вi] (6), как это требуется в соответствии с п. 2.11 алгоритма. Решение такой задачи может быть выполнено любыми известными в математике методами, но, как правило для сооружений порядок матриц [Ai] или [Bi] таков что без
привлечения ЭВМ
такую задачу решить невозможно. В настоящее время математическое обеспечение практически любой ЭВМ содержит стандартные программы по определению собственных значений и векторов матриц.
Матрицы, с которыми обращаются к ЭВМ для решения задачи на собственные значения, не
должны содержать обособленных составляющих. В противном случае
задача теряет смысл, что будет приводить к аварийным остановкам ЭВМ. Смысл задачи сводится к
решению уравнений в прямой форме (7)
или в обратной форме (8), которые написаны для случая матриц [А] и [B],
не содержащих обособленных составляющих. Для каждой обособленной составляющей [Ai] или
[Вi] уравнения записываются аналогично. Порядок
этих уравнений определяется порядком матриц [Ai] или [Вi],
в соответствии с которыми определяются векторы собственных
значений (коэффициентов форм колебаний) Каждая обособленная составляющая [Ai] или [Bi] определяет самостоятельную группу колебаний, для которой результаты решения по определению частот и форм целесообразно сводить в таблицы типа табл. 6. Найденные
коэффициенты форм колебаний Критерием точности решения задачи расчета режима свободных колебаний является проверка условий ортогональности найденных форм. Положения по этой проверке сформулированы в п. 2.13 алгоритма. Проверка сводится к заполнению табл. 7 для каждой самостоятельной группы колебаний. Решение задачи по расчету режима свободных колебаний представляет общую процедуру, единую для динамических расчетов сооружений на любые возмущения (сейсмические, ветровые, промышленные вибрации и т.д.). Поэтому, если отсутствуют специализированные комплексы автоматизированных расчетов на ЭВМ, то вычислительную процедуру расчета режима свободных колебаний целесообразно запрограммировать самостоятельно и использовать ее в индивидуальной практике проектной организации. Такую вычислительную процедуру целесообразно строить по структуре, показанной на рис. 1. Расчетные параметры сейсмического воздействияРассмотренные в Приложениях 1 и 2 пояснения относятся к любому динамическому расчету сооружения (на любые динамические воздействия). Динамический расчет сооружения на конкретное воздействие начинается с формулировки характера динамического возмущения и определения его расчетных параметров. Рассматриваемые в данных Рекомендациях методы динамического расчета сооружений учитывают пространственный характер сейсмического воздействия, которое по своей природе представляет фрагмент волнового поля движений грунта в основании сооружения при землетрясении. Общепризнанно [15], что поле сейсмических движений грунта имеет три явно выраженных фазы (Р, S и L), определяющиеся соответственно продольными (безвихревыми) Р-, поперечными (сдвиговыми или вихревыми) S- и поверхностными (которые также являются вихревыми) L-волнами, распространяющимися с определенными (имеющими свои закономерности изменения) конечными величинами фазовых скоростей. В начале наблюдается P-фаза, определенная продольными волнами, имеющими максимальную фазовую скорость. В этой фазе поле сейсмических движений является безвихревым и движение грунта определяется только его дилатацией (расширение-сжатие). Данная фаза характерна высокочастотными движениями грунта с малыми амплитудами, поэтому она не приводит к разрушению сооружений. После P-фазы наступает S-фаза, определяемая распространением поперечных волн, которые имеют меньшую фазовую скорость, чем P-волны. В S-фазе частотный состав ниже, а интенсивность движений существенно больше, чем в S-фазе. Основные повреждения сооружений при землетрясениях, по общепризнанному мнению [15], имеют место в S-фазе, которая определяет вихревое поле движений грунта. В вихревом поле движение грунта определяется его ротацией (искажением объема массива грунта). Поверхностные L-волны (Лэмба-Рэлея, Лява), грубо говоря, представляют некоторую модификацию S-волн с фазовой скоростью, зависящей от свойств структуры среды распространения волн. Фазовая скорость L-волн, как правило, еще меньше, чем S-волн. В L-фазе поле движений грунта носит общий характер и определяется дилатацией и ротацией массива грунта. Для L-фазы характерен более низкий частотный состав и более слабая интенсивность движений грунта, чем в S-фазе. Повреждения сооружений, начатые в S-фазе при землетрясениях, продолжают развиваться в L-фазе. Таким образом, основные повреждения и разрушения сооружений при землетрясениях определяются возмущениями в виде вихревого поля в S-фазе и поля общего характера в L-фазе. Эти поля определены дилатацией и ротацией соответствующего массива грунтового основания, результатом которых являются вектор ускорения поступательного движения и вектор углового ускорения вращения. Таким образом, волновой пространственной моделью сейсмического воздействия являются два трехкомпонентных вектора: ускорения поступательного движения и углового ускорения вращения. Векторы сейсмического воздействия характеризуются интенсивностью, спектральным составом и ориентацией в пространстве. Эти характеристики определяют расчетные параметры, алгоритм вычисления которых сформулирован в: п. 2.14 определяет интенсивность ускорения поступательного движения; п. 2.15 - интенсивность углового ускорения вращения; п. 2.16 - спектральный состав этих векторов; п. 2.17 - ориентацию векторов сейсмического воздействия. Рассмотрим формулировки этих пунктов в отдельности. Сейсмическое воздействие представляет поле движений грунта, в каждом элементарном объеме которого определены вектор ускорения поступательного движения и вектор углового ускорения вращения. На сооружение воздействует не все поле, а только его фрагмент, представляющий массив грунта в основании сооружения. Следовательно, в качестве расчетной величины воздействия на сооружение должна приниматься определенная в пределах этого фрагмента интенсивность движений грунта. В п. 2.14 сформулированы требования по определению осредненной интенсивности вектора ускорения поступательного движения грунта при сейсмическом воздействии. Под интенсивностью любого вектора понимается всегда положительная величина, равная его модулю, которая инвариантна по отношению к ориентации в пространстве осей отсчета. Расчетная интенсивность определяется модулем вектора где Параметры
интенсивности компонент вектора где Площади Sij в (52) образуют объем фрагмента рассматриваемого поля. Поэтому инвариант интенсивности ускорения поступательного движения грунта I по (51) является функцией от этого объема V. Такая функция является положительной и убывающей по мере увеличения V. Результаты обработки записей землетрясений и решения задач по оценке свойств поля сейсмического движения грунта [6], [7], [11], [13], [15] показывают, что эту зависимость можно аппроксимировать экспонентой вида I(V) = gAe-kv (м/с), (53) где g ≈ 10 м/с2 - ускорение силы тяжести; А (-) и k (м-3) - аппроксимирующие коэффициенты; V (м3) - учитываемый в расчете объем фрагмента рассматриваемого поля сейсмических движений грунта. Максимальная величина расчетного значения инварианта интенсивности ускорения поступательного движения грунта при сейсмическом воздействии имеет место в точке, когда V = 0 и I(0) = gA. Принятие этой величины безотносительно к рассматриваемому объему массива грунтового основания в качестве расчетной интенсивности сейсмического воздействия, как это рекомендовано в СНиП II-7-81, с физической точки зрения соответствует тому, что фазовые скорости распространения волн принимаются бесконечными, т.е. все точки основания имеют одну и ту же интенсивность движения. В этом случае в осреднении интенсивности по объему основания нет необходимости, но это, во-первых, противоречит физике явления, и, во-вторых, исключает для проектировщиков возможность создавать экономически выгодные и сейсмостойкие конструктивные решения. Путем увеличения расчетного объема V за счет устройства жестких (из монолитного железобетона) подземных этажей (заглубление сооружения) с развитыми в плане размерами (увеличение площади заглубленных этажей) можно достичь существенного снижения расчетной интенсивности. Важно определить целесообразное соотношение между дополнительным вкладом средств в подземную часть и экономией средств на надземной части сооружения. Это задача каждого конкретного варианта конструктивного решения проектируемого сооружения. Такой подход отвечает требованиям зарубежного опыта проектирования экономичных сейсмостойких сооружений. Опыт последствий землетрясений, происшедших на территориях, где распространены аналогичные конструктивные решения, показал, что крупные сооружения с развитой в плане и заглубленной нижней частью вполне удовлетворительно переносят сейсмические воздействия; в то время, как небольшие здания без развитой заглубленной части получают повреждения и разрушаются. Такие конструктивные решения совместно с основными требованиями по обеспечению развития пластических деформаций в несущих конструкциях являются основными критериями сейсмостойкости сооружений. Самостоятельную проблему представляет задача об определении объема V (53), в пределах которого вычисляется поток поля ускорений сейсмического движения грунта. Это - объем фундамента с прилегающим к нему массивом грунта. В первом приближении можно ограничиться вычислением потока через объем массива фундамента сооружения, но, учитывая сложность задачи, целесообразно свести аппроксимирующую функцию (53) к аналогичной экспоненциальной зависимости от меньшего размера сооружения в плане В и представить ее в виде (10), (11). Интенсивность вектора углового ускорения поля сейсмических движений грунта определяется в соответствии с требованиями п. 2.15. Инвариант интенсивности углового ускорения определяется в виде модуля вектора
где Параметры интенсивности компонент вектора углового ускорения определяются на основании теоремы Стокса, как циркуляции поля поступательного движения по соответствующим замкнутым контурам (L), которые равны потокам ротации этого же поля через поверхности (S), ограниченные этими контурами [4]: где Ji - мощность (интенсивность) вихревого поля по замкнутому контуру Li. Поле ускорения
ротации где ji - орты осей xi; × - знак векторного произведения. Развернув (56), получим следующие значения компонент поля ротации: Компоненты После осреднения в (55) компонент ротации (57) по площадям Sij, определяющим объем V, получим, что инвариантная интенсивность углового ускорения вращения сейсмического воздействия представляет в общем виде функцию от объема осреднения V, типа грунтов и инварианта интенсивности ускорения поступательного движения I (51), (52), т.е. Явный вид функций (58) устанавливается при исследованиях свойств полей сейсмического движения грунта. Обычно это функции убывающие по мере увеличения V возрастающие для более слабых грунтов по мере роста I. Нормировать такие функции по всей совокупности их аргументов сложно. Поэтому в п. 2.15 вводится функция (12), отнормированная (безотносительная) на величину I, которая является инвариантной характеристикой уровня ротации сейсмических движений грунта
Для каждого типа монохроматических волн эту характеристику можно получить в безразмерном виде. Сложнее привести ее к безразмерному виду для спектра волн. Поэтому целесообразно оставить W в размерном виде. Типы грунтов целесообразно принять по категориям СНиП II-7-81. Тогда (60) можно представить в виде W(V) = Ce-kv (1/м), (60) где С (м-1) и k (м-3) - аппроксимирующие коэффициенты, значения которых зависят от категории грунтов. Поскольку, как отмечалось выше, при определении объема осреднения V возникают сложности, то целесообразно заменить аппроксимирующую функцию (60) на функцию (12), (13), в зависимости от наименьшего размера сооружения в плане. Движения грунта
при землетрясениях определяются осциллирующими процессами. Поэтому,
кроме интенсивности векторов сейсмического воздействия, должен быть определен
их спектральный состав. Как известно, векторы могут быть определены двумя
способами: компонентами или модулем и
направляющими косинусами с дополнительной связью в виде их нормировки. Соответственно определяется спектральный состав компонент или модуля и направляющих косинусов. Данными о спектральном составе
динамического возмущения для расчета линейных систем являются
спектры коэффициентов динамичности, которые определяются в
результате ряда преобразований исходной информации. В работе [15] показана взаимосвязь между
спектрами Фурье детерминированных осциллирующих процессов и спектральными
плотностями случайных процессов, интегральными преобразованиями которых определяются спектры коэффициентов динамичности,
представляющие функции частот (периодов) и коэффициентов рассеяния (потерь)
энергии при колебаниях системы. В [15]
приведена структура необходимых для расчета спектров коэффициентов динамичности
при двух способах представления расчетной информации о векторах сейсмического воздействия. При компонентном способе представления информации
требуется исходить из коэффициентов динамичности компонент векторов, а при
пространственно-инвариантном способе - из
коэффициентов динамичности модулей и направляющих косинусов. С помощью этих коэффициентов
динамичности вычисляются коэффициенты динамичности отдельных форм колебаний (24), которые, как показано в [15],
представляются отдельными квадратичными формами со
структурой, зависящей от способа представления
информации и от учитываемых корреляционных связей
между векторами воздействия и их составляющими. В [15] дан анализ этих квадратичных форм для обоих
способов представления информации. Показано,
что при отсутствии корреляции данные квадратичные формы принимают однородный
вид (представляют сумму квадратов отдельных составляющих), для которого становится
возможным применение упрощающих преобразований
и сведение результатов к простым формулам для определения коэффициентов динамичности отдельных форм колебаний. В настоящих Рекомендациях целесообразно привести
компонентный способ представления спектральной информации о векторах воздействия.
При отсутствии корреляций коэффициенты динамичности отдельных форм колебаний
определяются в виде (24), а спектральная информация
о векторах где Т - период собственных колебаний рассматриваемого сооружения. Ненулевые
диагональные члены матриц определяются по автокорреляции процессов компонент векторов - в настоящее время данных по коэффициентам динамичности, определенным по взаимной корреляции между процессами компонент векторов воздействия очень мало и не представляется возможным их нормировать; - при учете этих корреляций формулы по определению коэффициентов динамичности для отдельных форм колебаний (24) существенно усложняются [15]. Для каждой из матриц (61), (62) диагональные компоненты приняты равными между собой. Тогда (61), (62) можно представить в виде: где Е - единичная матрица. Поскольку
настоящие Рекомендации составлены в развитие СНиП II-7-81 [17], то Коэффициенты
динамичности процессов углового ускорения сейсмического воздействия Следующей
характеристикой сейсмического воздействия являются параметры его ориентации в
пространстве, которые определяются в
соответствии с требованиями п. 2.17. Ориентация векторов
сейсмического воздействия в пространстве определяется по их направляющим
косинусам, которые отсчитываются относительно соответствующих осей. В п.
2.17
описаны эти оси и даны условия нормировки
направляющих косинусов для векторов - наиболее вероятные значения для заданного района строительства, которые следует принимать как проверочные. Эти значения рекомендуется принимать с учетом данных конкретной сейсмологической обстановки; - основные расчетные значения направляющих косинусов, расчет на которые является обязательным. Сейсмическое воздействие
может иметь произвольную ориентацию в пространстве. Поэтому основные расчетные значения
направляющих косинусов должны быть приняты
такими, чтобы при них реализовывался максимум динамической реакции для рассматриваемой формы
колебаний. Максимум любого параметра
динамической реакции имеет место при максимуме коэффициента динамичности для рассматриваемой
формы колебаний (24). Поэтому задача
сводится к исследованию на максимум функции (24) по параметрам - векторы - между векторами сейсмического воздействия существует определенная взаимосвязь, т.е. что приводит к соответствующей
зависимости между Первая задача
решается при свободной вариации Расчет режима вынужденных колебанийРасчет режима вынужденных колебаний выполняется в соответствии с Рекомендациями п.п. 2.18 и 2.19 или 2.20. В соответствии
с п. 2.18
для каждой формы колебаний и для каждой группы
расчетных значений
направляющих косинусов векторов
где a(j)i и b(j)i - коэффициенты (23) для j-ой формы колебаний; Mj - масса сооружения, приведенная к j-ой форме, значения которой располагаются по главной диагонали таблицы проверки условий ортогональности форм колебаний (см. табл. 7) или вычисляются по формуле
Далее в расчете режима вынужденных колебаний выполняются требования либо п. 2.19, либо п. 2.20, в зависимости от того, какой метод расчета был принят при описании упругих свойств расчетной динамической модели. Если расчет упругой
системы выполнялся согласно п. 2.7 по методу сил и от действия единичных сил и моментов определялись перемещения для формирования матрицы податливости (40) (см. табл. 2),
а также определялось соответствующее напряженно-деформированное
состояние рассчитываемых несущих конструкций, то расчетными параметрами
являются векторы сейсмических сил и моментов, которые вычисляются по формулам (25), приведенным в п. 2.19. Векторы
сейсмических сил и моментов по (25)
вычисляются для всех значений β(i)j (см. табл. 9),
т.е. для каждой формы колебаний и для каждого
варианта ориентации векторов Если расчет
упругой системы выполнялся согласно п. 2.8 по методу деформаций и от действия
единичных перемещений и угловых поворотов определялись
реакции для формирования матрицы жесткости (44) (см. табл. 4), а также определялось
соответствующее напряженно-деформированное
состояние рассчитываемых несущих конструкций, то
основными расчетными параметрами являются векторы перемещений центров масс и
углов вращения масс, которые вычисляются в
виде (26). Векторы перемещений и углов
вращения (26) вычисляются для каждой формы колебаний и для каждого
варианта ориентации Алгоритм определения основных расчетных параметров (сил и моментов по формуле (25) или перемещений и углов вращения по (26)) построен на основе замкнутых решений линейных дифференциальных уравнений движения масс сооружения в предположении упругой (линейной) работы материала несущих конструкций при малых величинах перемещений и углов вращения масс. Внешнее воздействие принимается по нормированным обработкам записей реальных землетрясений, при которых, в зависимости от заложенных резервов прочности в сооружении, как правило, развиваются пластические деформации, местные повреждения, приводящие к снижению сейсмической нагрузки. В рамках линейных методов расчета эти явления невозможно учесть. Поэтому при определении основных расчетных параметров по (25) или (26) вводится коэффициент k, учитывающий допускаемый уровень накопления пластических деформаций и другие местные повреждения, не приводящие к разрушению сооружения в целом. Значение этого коэффициента зависит от вида рассчитываемого сооружения и всегда k ≤ 1. Если сооружения относятся к категории особо ответственных и в нем не допускается образование каких-либо местных повреждений, то k всегда должен приниматься равным единице. В других случаях, когда допускается образование пластических деформаций, значение k всегда меньше единицы и зависит от индивидуальной способности принятой конструктивной схемы сооружения к образованию и накоплению в ней пластических деформаций. В ходе выполнения расчетно-проектных работ значение k может корректироваться в зависимости от рассматриваемой конструктивной схемы и должно утверждаться заказчиком применительно к окончательному принятому варианту, или оцениваться углубленными исследованиями. Определение расчетных значений внутренних усилий в несущих конструкциях сооруженияРассматриваемые методы позволяют определять внутренние усилия в несущих конструкциях без дополнительного статического расчета сооружения на действие найденных значений сейсмических сил и моментов. Исходными данными для определения внутренних усилий в рассматриваемых несущих конструкциях являются данные статического расчета (см. табл. 1) на действие единичных сил и моментов по п. 2.7 при формировании матрицы податливости [δ] или аналогичные данные от действия единичных перемещений и углов вращения (см. табл. 3) по п. 2.8 при формировании матрицы жесткости [r], а также фактические величины сейсмических сил и моментов (см. п. 2.19, табл. 13) или соответствующие фактические величины перемещений и углов вращения (см. п. 2.20, табл. 14). Задача сводится к корректировке единичных значений внутренних усилий (табл. 1 или табл. 3) на фактические значения нагрузки по п. 2.19 (табл. 13) или на фактические значения перемещений и углов вращения по п. 2.20 (табл. 14). Алгоритм этого расчета сформулирован в п.п. 2.21, 2.22, где п. 2.21 и п. 2.22 относятся к различным методам. Поэтому, в зависимости от принятого в конкретном случае метода, следует выполнять требования только одного из этих пунктов. Если расчет упругих свойств выполнялся в соответствии с требованиями п. 2.7 по методу сил для построения матрицы податливости [δ] и при этом определялись внутренние усилия от действия единичной нагрузки (см. табл. 1), а также по п. 2.19 вычислялись фактические величины сейсмических сил и моментов (см. табл. 13), то необходимо выполнять требования п. 2.21 по корректировке данных табл. 1 на данные табл. 13. В соответствии с (27), внутренние силы и моменты определяются произведением единичных значений (см. табл. 1) на фактические величины сейсмических сил и моментов (см. табл. 13) с последующим суммированием по всем силам и моментам, относящиеся к рассматриваемой форме колебаний. Таким образом, для каждой формы колебаний и при каждом варианте ориентации векторов сейсмического воздействия определяются требуемые для расчета внутренние усилия. Результаты такого расчета сводятся в табл. 15. Если расчет упругих свойств выполнялся в соответствии с требованиями п. 2.8 по методу деформаций для построения матрицы жесткости и при этом определялись внутренние усилия от действия единичных перемещений и углов поворота (см. табл. 3), а также по п. 2.20 вычислялись фактические величины перемещений и углов вращения масс (см. табл. 14), то необходимо выполнить требования п. 2.22 по корректировке данных табл. 3 на данные табл. 14. Согласно (28), внутренние усилия (силы и моменты) определяются произведением единичных значений (см. табл. 3) на фактические величины перемещений и углов вращения (см. табл. 14) с последующим суммированием по всем перемещениям и углам вращения, относящимся к рассматриваемой форме колебаний. В результате для каждой формы колебаний и для каждого варианта ориентации векторов сейсмического воздействия определяются требуемые для расчета внутренние усилия, которые сводятся в табл. 16. Данные табл. 15 и 16 представляют эквивалентный результат. Поэтому дальнейшая обработка этих данных выполняется безотносительно к применяемым методам расчета. Эта обработка выполняется в соответствии с п.п. 2.23-2.24. Результаты табл.
15 и 16 представляют внутренние усилия для
каждого варианта ориентации векторов сейсмического воздействия по всем формам колебаний.
Согласно п. 2.23 для каждого варианта ориентации векторов
сейсмического воздействия определяются
расчетные значения внутренних усилий, как
среднеквадратичные величины (см. п. 2.10 СНиП II-7-81) значений, соответствующих отдельным формам колебаний.
Следует иметь в виду, что каждый вариант
ориентации векторов сейсмического воздействия по (22) определяет максимум значений
внутренних
усилий по соответствующей форме колебаний, а все другие формы колебаний будут
приводить к малой добавке при определении
расчетных значений внутренних усилий. С учетом определения максимума реакции по
ориентации векторов воздействия (см. (22)) вопрос
о суммировании эффектов от отдельных форм колебаний приобретает менее острый характер.
Такая ситуация выражается более явно когда векторы коэффициентов
форм колебаний Согласно п. 2.24 выполняется анализ расчетных
значений внутренних усилий по данным табл. 17. Из расчетных значений
внутренних усилий, соответствующих различным
вариантам ориентации Список литературы1. Инструкция по определению расчетной сейсмической нагрузки для зданий и сооружений. - М.: Госстройиздат, 1962. - 127 с. 2. Йованович П. Статика сооружений в матричной форме. - М.: Стройиздат, 1984. - 271 с. 4. Ландау Л. Д., Лифшиц Е. М. Теория поля. - М.: Наука, 1973. - 504 с. 5. Лурье А. И. Аналитическая механика. - М.: Наука, 1961. - 336 с. 8. Николаенко Н. А., Назаров Ю. П. Динамика и сейсмостойкость пространственных конструкций и сооружений // Исследования по теории сооружений. - 1977. -Вып. XXIII. - С. 66-98. 17. СНиП II-7-81. Строительство в сейсмических районах. - Ч. II, гл. 7. СОДЕРЖАНИЕ
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/11519/
На эту страницу сайта можно сделать ссылку:
На правах рекламы: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|