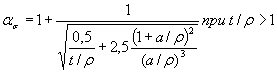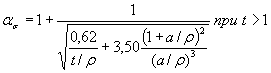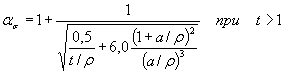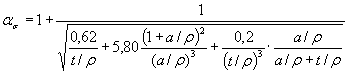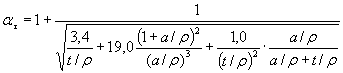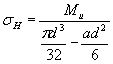
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
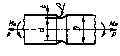
Вернуться в "Каталог СНиП"ГОСТ 25.504-82* Расчеты и испытания на прочность. Методы расчета характеристик сопротивления усталости.
Дата введения 01.07.83 - медианных значений пределов выносливости на базе 107 циклов; - пределов выносливости для заданной вероятности разрушения на базе 107 циклов; - коэффициента вариации пределов выносливости; - показателя наклона левой ветви кривой усталости в двойных логарифмических координатах - абсциссы точки перелома кривой усталости; - коэффициента чувствительности к асимметрии цикла напряжений; - предельных амплитуд при асимметричных циклах нагружения; - параметров уравнения кривой малоцикловой усталости (в пределах до 105 циклов) при: растяжении - сжатии, изгибе и кручении, - симметричных и асимметричных циклах напряжений или деформаций, изменяющихся по простому периодическому закону с постоянными параметрами, абсолютных размерах поперечного сечения детали до 300 мм, наличии и отсутствии концентрации напряжений, температуре от минус 40°С до плюс 100°С, наличии и отсутствии агрессивной среды, частоте нагружения в пределах 1 - 300 Гц. Стандарт не распространяется на методы расчета характеристик сопротивления усталосп сварных конструкций и их элементов. Область применения стандарта ограничивается случаями, для которых в тексте стандарта приложений имеются все исходные и справочные данные. Выбор требуемой номенклатуры характеристик сопротивления много- и малоцикловой усталости определяется в каждом конкретном случае задачами и методом расчета по действующим отраслях нормативно-техническим документам. Термины, определения и обозначения, применяемые в стандарте, - по ГОСТ 23207. Обозначения, применяемые в стандарте, приведены в приложении 1. Размерность напряжений - МПа, геометрических размеров - мм. Настоящий стандарт унифицирован со стандартами ГДР ТГЛ 19340/03 и ТГЛ 19340/04. (Измененная редакция, Изм. № 1). СОДЕРЖАНИЕ 1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ МАШИН И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ1.1. Определение медианных значений пределов выносливостиМедианные значения пределов выносливости
деталей машины в номинальных напряжениях - при растяжении - сжатии или изгибе
- при кручении
Медианные значения пределов выносливости
деталей Примечания: 1. При наличии коррозионных воздействий в формулы (2) и (5) вместо KFследует подставлять значения Kкор 2. При отсутствии экспериментальных
данных ориентировочно величины
где
1.2. Определение эффективных коэффициентов концентрации напряжений Кσ, Кτ и отношений Kσ/Kdσ, Kτ/Kdτ1.2.1. Коэффициенты Кσ, Кτ и отношения Kσ/Kdσ, Kτ/Kdτ определяют по экспериментальным данным или путем расчета. 1.2.2. Определение Кσ , Кτ, Kσ/Kdσ и Kτ/Kdτ - по экспериментальным данным. Коэффициенты Кσ, Кτ могут определяться экспериментально на геометрически подобных образцах диаметром d или толщиной h поперечного сечения не менее 40 мм, если d или h рассчитываемой детали превышают это значение. Если d или h рассчитываемой детали меньше 40 мм, то при экспериментальном определении Кσ, Кτ целесообразно вести испытания на натурных деталях или моделях тех же поперечных размеров. Для ряда деталей экспериментально полученные значения Кσ, Кτ и Kσ/Kdσ, Kτ/Kdτ приведены в приложении 2 (черт. 1-7, 13-16). Значения (Kσ/Kdσ)0 для валов с напрессованными деталями (при наличии коррозии трения) при изгибе представлены на черт. 1 приложения 2. При σB > 500 МПа и ρ < 30 МПа следует учитывать соответствующие поправочные
коэффициенты
(Измененная редакция, Изм. № 1). * Формула 9. (Исключена, Изм. № 1). 1.2.3. Определение Кσ, Кτ и Kσ/Kdσ, Kσ/Kdσ методом расчета
где Определение относительного критерия подобия усталостного разрушения Θ, величин vσ, vτ и функции F(Θ , v) приведено в пп. 1.5 и 1.8. 1.2.3.2. Если известны только
величины ασ, ατ
и
Коэффициент n вычисляют по формуле
или по черт. 14
приложения 2 в зависимости от значений относительного градиента напряжений Таблица 1
Примечание. 1.2.3.3. В приближенных расчетах значения Кσ и Кτ вычисляют по формулам: Кσ =1 + q(ασ-1), (18)* Кτ =1 + q(ατ-1), (19) где значения коэффициентов чувствительности металла к концентрации напряжений q определяют по черт. 15 приложения 2. 1.3. Определение коэффициентов К11.2.3.1.-1.3. (Измененная редакция, Изм. № 1). 1.3.1. Коэффициент К1 для легированных сталей определяют по черт. 16 приложения 2 или по формуле
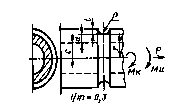
где d0 = 7,5 мм - диаметр гладкого лабораторного образца; K1 = 0,74 для d > 150 мм. Для углеродистых сталей К1 = 1. 1.3.2, 1.3.3. (Исключены, Изм. № 1). * Формулы 16 и 17. (Исключены, Изм. № 1). 1.4. Определение теоретических коэффициентов концентрации напряжений ασ, ατ1.4.1. Коэффициенты ασ, ατ определяют по теоретическим решениям или на основе измерений с помощью поляризационно-оптического метода, тензометрирования и т.п. (приложение 3, черт. 1-47). 1.4.2. Для определения теоретических коэффициентов концентрации напряжений в деталях, изображенных в табл. 2, могут быть использованы также номограммы, приведенные на черт. 48 и 49 приложения 3. Примечания: 1. Пример использования номограмм для элементов с двусторонней внешней выточкой при изгибе. Дано: ρ = 2,5 мм; t = 15 мм; а = 95 мм. Находим Как вытекает из табл. 2, для 2. Пример использования номограммы для элементов с внешней выточкой и осевым отверстием при изгибе. Дано: ρ = 4 мм; а = 13 мм; t = 36 мм; r = 25 мм. Находим Как указано в примере 1 при Теперь переходим к черт. 49 и смещаемся вверх по вертикали при значении Таблица 2 Конструктивные случаи для определения теоретических коэффициентов концентрации ασ и ατ по номограмме (приложение 3, черт. 48, 49)
1.4.3. При обработке результатов на ЭВМ коэффициенты концентрации напряжений ασ для деталей, указанных на черт. 20-22, 27 и 28 приложения 3, вычисляют по формуле
где коэффициенты A, B, С и Z определяют по табл. 3 (а = d/2 или а = b/2), а в остальных случаях ασ определяют по формулам, приведенным на черт. 1-3, 6-11, 14-19 приложения 3. Примечание. Формула (25) является приближенной и дает отклонения до 10 %-20 % в запас прочности. * Формулы 21-24. (Исключены, Изм. № 1). Таблица 3 Значения коэффициентов для вычисления ασ по формуле (25)
1.5. Определение значения относительного критерия подобия усталостного разрушения1.5.1. Относительный критерий подобия 0 вычисляют по формуле
L выражается в мм,
Значения функции Таблица 4 Значения функции F (Θ, v)
В формуле для определения F(Θ, v) параметр v принимает значения vaσ при изгибе и растяжении-сжатии и vτ - при кручении. 1.6. Определение параметра L1.6.1. При круговом изгибе или растяжении-сжатии, а также при кручении круглых стержней с кольцевыми канавками, с переходом от одного сечения к другому по галтели, с резьбой или гладких L = πd. При изгибе в одной плоскости круглых стержней L = 0,08 πd. Если при растяжении-сжатии или изгибе деталей только часть периметра рабочего сечения прилегает к зоне повышенной напряженности, то L вычисляют по формулам, приведенным на черт. 2 приложения 4. 1.7.
Определение относительного градиента первого главного или касательного
напряжений
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
σВ, МПа |
ка |
σВ, МПа |
ка |
|
До 600 |
0,90 |
Св. 900 до 1200 |
0,83 |
|
Св. 600 до 900 |
0,86 |
» 1200 |
0,80 |
2. ОПРЕДЕЛЕНИЕ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ ДЕТАЛЕЙ МАШИН И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ДЛЯ ЗАДАННОЙ ВЕРОЯТНОСТИ РАЗРУШЕНИЯ [σ-1Д]р
2.1. При наличии достаточного объема статистической
информации для оценки коэффициента вариации пределов выносливости деталей машин
(![]() или
или ![]() ), используя вычисленное для заданной базы по формуле (1) или (4) медианное значение
предела выносливости детали (
), используя вычисленное для заданной базы по формуле (1) или (4) медианное значение
предела выносливости детали (![]() , или
, или ![]() ), определяют пределы выносливости
детали на той же базе для любых заданных вероятностей разрушения Р в предположении справедливости
нормального закона распределения по формулам:
), определяют пределы выносливости
детали на той же базе для любых заданных вероятностей разрушения Р в предположении справедливости
нормального закона распределения по формулам:
![]() , (31)
, (31)
![]() , (32)
, (32)
где zp - квантиль нормального распределения, соответствующая заданной вероятности разрушения Р.
3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ВАРИАЦИИ ПРЕДЕЛОВ ВЫНОСЛИВОСТИ
ДЕТАЛЕЙ МАШИН И ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
3.1. Коэффициент вариации предела выносливости детали вычисляют по формуле
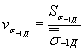 , (33)
, (33)
где ![]() и
и
![]() - среднее квадратическое отклонение и среднее (на
совокупности всех плавок) значение предела выносливости детали соответственно.
- среднее квадратическое отклонение и среднее (на
совокупности всех плавок) значение предела выносливости детали соответственно.
Результирующий коэффициент вариации предела выносливости детали при отсутствии сварки, поверхностного упрочнения и при стабильной технологии вычисляют по формуле
![]() , (34)
, (34)
|
где
|
- коэффициент вариации максимальных разрушающих напряжений в зоне концентрации, соответствующий пределам выносливости деталей (при испытании идентичных деталей, изготовленных из металла одной плавки, связанный со структурой неоднородностью металла (наличием различных фаз, включений, искажений кристаллической решетки и т.д.); |
|
|
- коэффициент вариации средних (в пределах одной плавки) значений пределов выносливости гладких лабораторных образцов диаметром 7,5 мм, учитывающий межплавочное рассеяние механических свойств металла и вычисляемый по формуле |
![]() , (35)
, (35)
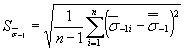 ; (36)
; (36)
![]() , (37)
, (37)
|
где
|
-
значение |
|
n |
- число плавок; |
|
|
- коэффициент вариации теоретического коэффициента концентрации напряжений ασ, учитывающий отклонения фактических размеров деталей (особенно в зонах концентрации напряжений) от номинальных (в пределах допусков). |
При нестабильной технологии,
неоднородности свойств металла, наличии остаточных напряжений и технологических
дефектов коэффициенты вариации предела выносливости деталей ![]() определяют путем
проведения усталостных испытаний деталей.
определяют путем
проведения усталостных испытаний деталей.
3.2.
Определение коэффициентов вариации 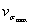
3.2.1. При достаточно стабильной
технологии, однородности свойств металла в объеме детали, отсутствии остаточных
напряжений коэффициенты вариации максимальных разрушающих напряжений ![]() вычисляют по формуле
вычисляют по формуле
![]() . (38)
. (38)
3.3.
Определение коэффициентов вариации 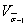
Коэффициент ![]() определяют по
статистическим данным о межплавочном рассеянии пределов выносливости по
формулам (35)-(37).
определяют по
статистическим данным о межплавочном рассеянии пределов выносливости по
формулам (35)-(37).
Если данных по межплавочному рассеянию
величин ![]() нет, то, учитывая
практически линейную зависимость между пределами выносливости и пределами
прочности, в первом приближении допускают
нет, то, учитывая
практически линейную зависимость между пределами выносливости и пределами
прочности, в первом приближении допускают
![]() =
= ![]()
где ![]() - коэффициент
вариации предела прочности металла на множестве всех плавок (
- коэффициент
вариации предела прочности металла на множестве всех плавок (![]() = 0,04-0,10).
= 0,04-0,10).
3.4.
Определение коэффициентов вариации 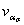
Колебания радиусов кривизны в зоне концентрации напряжений ρ характеризуются коэффициентами вариации vρ. Коэффициенты вариации находят по результатам измерения партии деталей (не менее 30-50 шт.) в условиях производства.
Среднее значение ![]() , среднее квадратическое отклонение sρ радиуса кривизны ρ и коэффициент вариации vρ
вычисляют по формулам:
, среднее квадратическое отклонение sρ радиуса кривизны ρ и коэффициент вариации vρ
вычисляют по формулам:
![]() , (39)
, (39)
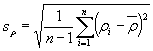 , (40)
, (40)
![]() . (41)
. (41)
Зависимость ασ от ρ представляют функцией
ασ = φ(ρ). (42)
Коэффициент вариации ![]() вычисляют по формуле
вычисляют по формуле
![]() (43)
(43)
где ![]() - среднее значение ασ, соответствующее ρ
=
- среднее значение ασ, соответствующее ρ
= ![]() ;
;
![]() - абсолютное значение производной, которое
соответствует средним значениям определяющих параметров.
- абсолютное значение производной, которое
соответствует средним значениям определяющих параметров.
3.4.3. Для нахождения производной в выражении (43) допускается осуществлять линейную аппроксимацию функции (42) в окрестности заданных значений параметров, используя уравнение прямой, проходящей через две точки
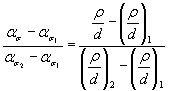 , (44)
, (44)
|
где
|
- заданное значение отношения параметров ρ и d (вместо ρ/d может быть ρ/t и т.п.); |
|
|
-
отношения |
|
|
- значения ασ, соответствующие (ρ/d)2 и (ρ/d)1. |
4. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КРИВЫХ УСТАЛОСТИ m И NG И КОЭФФИЦИЕНТОВ ЧУВСТВИТЕЛЬНОСТИ К АСИММЕТРИИ ЦИКЛА НАПРЯЖЕНИЙ Ψσ И Ψτ
4.1. Для расчета на прочность левую наклонную часть кривой усталости представляют в виде
![]() , (45)
, (45)
|
где m |
- показатель наклона кривой усталости в двойных логарифмических координатах; |
|
NG |
- абсцисса точки перелома кривой усталости. |
4.2. Величина NG в большинстве случаев колеблется в пределах NG = 106 - 3 ∙ 106 циклов. В расчетах на прочность при переменных напряжениях, когда отсутствуют данные натурных усталостных испытаний, принимают в среднем NG =2 ∙ 106 циклов.
4.3. Величины m для деталей изменяются в пределах 3-20, при этом с ростом коэффициента снижения предела выносливости K уменьшается m. Зависимость между K и m принимают приближенно в виде
![]() , (46)
, (46)
где
![]() (47)
(47)
4.4. Значения Ψσ и Ψτ вычисляют по формулам:
Ψσ = 0,02 + 2 - 10-4 σB, (48)
Ψτ = 0,01 + 10-4 - σB, (49)
где σB в МПа.
Для деталей с концентрацией
напряжений коэффициенты влияния асимметрии цикла ![]() и
и ![]() вычисляют по
формулам:
вычисляют по
формулам:
![]() , (50)
, (50)
где K- коэффициент, определяемый по формулам (2), (5).
Для легированных сталей
допускается вычислять коэффициенты ![]() и
и ![]() по формулам:
по формулам:
![]() , (51)
, (51)
![]() , (52)
, (52)
4.5. Предельные амплитуды для деталей при асимметричном цикле нагружения вычисляют по формулам:
![]() , (53)
, (53)
![]() , (54)
, (54)
5. ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ
ХАРАКТЕРИСТИК СОПРОТИВЛЕНИЯ
МАЛОЦИКЛОВОЙ УСТАЛОСТИ
5.1. Расчет малоцикловой долговечности выполняется на основе анализа местных деформаций. К малоцикловой относят область чисел циклов до разрушения < 5 ∙ 104-105, когда становится выраженным упругопластический характер деформированного состояния конструкции. Рассматривают условия нагружения, при которых максимальные деформации достигают 0,5 %-1,0 %.
5.2. При определении малоцикловой долговечности и оценке накопления повреждений должны быть следующие данные:
- циклические упругопластические и односторонне накопленные деформации в максимально напряженных зонах конструкции:
- располагаемая пластичность материала εf;
- кривая малоцикловой усталости конструкционного материала (N =f(ε)(k)).
5.3. Определение напряжений и деформаций
5.3.1. Напряженно-деформированное состояние и его поцикловое изменение в максимально напряженных зонах конструкции определяют расчетным или экспериментальным методами, в том числе по данным тензометрических измерений на моделях и натурных конструкциях для заданных или эквивалентных нагрузок.
5.3.2. Расчетное определение напряженно-деформированного состояния элементов конструкций выполняется решением соответствующих задач малоциклового нагружения в циклической упруго-пластической постановке либо в замкнутой форме, либо численными методами.
5.3.3. Для приближенных оценок малоцикловой прочности элементов конструкций, работающих при нагрузках, вызывающих в зонах концентрации напряжений выход материала за пределы упругости, деформации и напряжения приближенно определяют с использованием интерполяционных зависимостей типа
![]() , (55)
, (55)
![]() , (56)
, (56)
|
где
|
- упругопластический коэффициент концентрации напряжений; |
|
|
- упругопластический коэффициент концентрации деформаций; |
|
|
- циклический упругопластический коэффициент концентрации напряжений; |
|
|
- циклический упругопластический коэффициент концентрации деформаций. |
Зависимость используется для ασ ≤ 3,5. При больших значениях ασ применение формулы дает результаты, идущие в запас прочности.
Для вычисления значения циклических
упругопластических коэффициентов концентрации ![]() и
и ![]() , кроме известных значений теоретического коэффициента
концентрации ασ,
необходимо знать зависимость напряжения от деформации при циклическом
упругопластическом деформировании.
, кроме известных значений теоретического коэффициента
концентрации ασ,
необходимо знать зависимость напряжения от деформации при циклическом
упругопластическом деформировании.
5.4. Определение диаграмм статического и циклического деформирования
5.4.1. Диаграмма статического и циклического деформирования характеризует зависимость напряжения от деформации при статическом или циклическом нагружении. Диаграммы деформирования определяют по данным испытаний при статическом или циклическом нагружении, проводимых по ГОСТ 25.502 и ГОСТ 1497.
5.4.2. Аналитически диаграммы циклического деформирования интерпретируют в форме обобщенной диаграммы циклического деформирования. Обобщенная диаграмма циклического деформирования отражает зависимость напряжения от деформации по параметру числа полуциклов нагружения. Диаграмму рассматривают в координатах S- ε (черт. 1). Основное свойство обобщенной диаграммы заключается в том, что для мягкого, жесткого и промежуточных между мягким и жестким нагружениями все конечные и текущие точки диаграмм деформирования k-го полуцикла нагружения, полученные при различных уровнях исходных деформаций, укладываются на одну и ту же для данного полуцикла нагружения кривую. Схема обобщенной диаграммы деформирования приведена на черт. 1.
Схема обобщенной диаграммы циклического деформирования
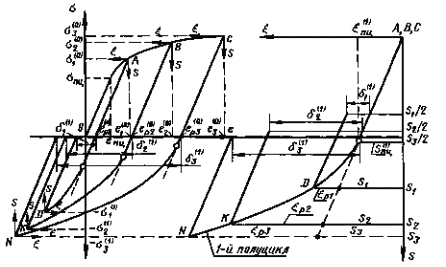
Черт. 1
Исходное нагружение происходит в
соответствии с диаграммой статического деформирования О, A, B, С, рассматриваемой в координатах σ-е с
началом в точке О. Процесс
исходного нагружения доводят до определенного значения напряжений и деформаций,
например до состояний А, В,
С. Таким образом напряжения исходного нагружения составят ![]() ,
, ![]() и
и ![]() , а деформации -
, а деформации - ![]() ,
, ![]() и
и ![]() соответственно. После
разгрузки, происходящей в соответствии с модулем упругости материала, остаются
величины пластических деформаций
соответственно. После
разгрузки, происходящей в соответствии с модулем упругости материала, остаются
величины пластических деформаций ![]() ,
, ![]() и
и ![]() . Исходное
нагружение и разгрузка образуют нулевой (k = 0) полуцикл нагружения.
. Исходное
нагружение и разгрузка образуют нулевой (k = 0) полуцикл нагружения.
Реверс нагружения происходит по своей для
каждой степени исходного нагружения диаграмме деформирования, достигая,
например, состояний D K, N, соответствующих напряжениям ![]() ,
, ![]() и
и ![]() причем для
симметричного цикла мягкого нагружения
причем для
симметричного цикла мягкого нагружения ![]() ,
,![]() и
и ![]() . Реверсивное нагружение и последующая разгрузка образуют
первый (k = 1) полуцикл нагружения, а совокупность нулевого и
первого полуциклов - первый (N = 1) цикл нагружения.
. Реверсивное нагружение и последующая разгрузка образуют
первый (k = 1) полуцикл нагружения, а совокупность нулевого и
первого полуциклов - первый (N = 1) цикл нагружения.
Обобщенная диаграмма циклического деформирования
строится для каждого отдельного полуцикла нагружения в координатах S- ε с началом в точке разгрузки и для каждого
рассматриваемого состояния нагружения. Для первого (k = 1) полуцикла нагружения (при исходных уровнях
напряжений ![]() ,
, ![]() и
и ![]() начало координат S- ε помещают в точки А, В, С. При этом кривая деформирования
рассматриваемого полуцикла включает в себя участок нагружения этого полуцикла и
участок разгрузки предыдущего.
начало координат S- ε помещают в точки А, В, С. При этом кривая деформирования
рассматриваемого полуцикла включает в себя участок нагружения этого полуцикла и
участок разгрузки предыдущего.
Для построения обобщенной диаграммы циклического деформирования точки начала разгрузки для данного полуцикла нагружения совмещают. На правой части черт. 1 для k-1 точки А, В, С совмещены и образована единая зависимость между напряжениями и деформациями A, B, C, D, K, N.
Аналогичные построения делают и для последующих полуциклов нагружения. В общем случае, в связи с процессами циклического упрочнения или разупрочнения материала, обобщенные диаграммы деформирования для различных полуциклов нагружения отличаются друг от друга. Обобщенная диаграмма циклического деформирования оказывается неизменной (начиная с k = 1) только для циклически стабильных материалов.
5.4.3. Для приближенных расчетов допускается использовать диаграммы циклического деформирования, образуемые удвоением статической диаграммы деформирования материала.
5.4.4. Аппроксимация диаграмм деформирования выполняется для расчетных приложений степенными функциями:
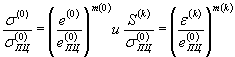 (57)
(57)
![]() ,
,
|
где
|
- напряжение и деформация предела пропорциональности материала при статическом нагружении; |
|
m(0) и m(k) |
- показатели упрочнения материала в упругопластической области, определяемые по диаграммам статического и циклического деформирования при степенной аппроксимации. |
При этом циклический модуль упрочнения имеет вид:
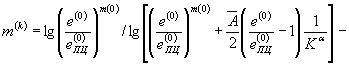 (58)
(58)
для циклически упрочняющихся материалов, для которых m(k-1) < m(k)
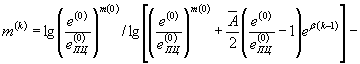 (59)
(59)
для циклически разупрочняющихся материалов, для которых m(k-1) > m(k)
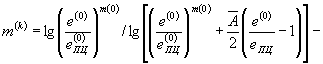 (60)
(60)
для циклически стабилизирующихся материалов, у которых m(k-1) = m(k)
При линейной аппроксимации диаграммы статического и циклического деформирования имеют вид:
![]() (61)
(61)
(при σ(0)
> ![]() и S(k) >
и S(k) > ![]() ),
),
|
где
|
- показатели упрочнения материала в упругопластической области, определяемые по диаграмме статического и циклического деформирования при линейной аппроксимации; |
|
|
- для циклически упрочняющихся материалов; |
|
|
- для циклически разупрочняющихся материалов; |
|
|
- для циклически разупрочняющихся материалов. |
5.4.5. По статическим диаграммам деформирования определяют пределы
пропорциональности, текучести и прочности, равномерное и общее удлинение (ГОСТ 1497), по диаграммам циклического деформирования - пределы
пропорциональности и текучести по параметру числа циклов или полуциклов
нагружения, коэффициенты ![]() , α, β, характеризующие сопротивление
циклическому деформированию, циклическое упрочнение, разупрочнение,
стабилизацию.
, α, β, характеризующие сопротивление
циклическому деформированию, циклическое упрочнение, разупрочнение,
стабилизацию.
5.4.6. Коэффициент ![]() характеризует связь между деформацией
исходного нагружения е(0) и шириной петли гистерезиса δ(1) в
первом полуцикле при мягком нагружении. Определяют из выражения
характеризует связь между деформацией
исходного нагружения е(0) и шириной петли гистерезиса δ(1) в
первом полуцикле при мягком нагружении. Определяют из выражения
![]() = δ(1)/ (е(0) -
= δ(1)/ (е(0) - ![]() ). (62)
). (62)
Полученную совокупность
экспериментальных величин ![]() (по результатам
испытания серии порядка 5-10 образцов при различных значениях исходной
деформации е(0))
обрабатывают с использованием метода наименьших квадратов или другим способом
осреднения.
(по результатам
испытания серии порядка 5-10 образцов при различных значениях исходной
деформации е(0))
обрабатывают с использованием метода наименьших квадратов или другим способом
осреднения.
5.4.7. Коэффициенты α и β определяют по полученным при мягком нагружении экспериментальным данным lg δ(k) - lgk (для случая циклического упрочнения) и lg δ(k) - k (для циклического разупрочнения). Величины α или β для рассматриваемого образца вычисляют по формулам (черт. 2):
![]() (63)
(63)
где δ(k) - ширина петли гистерезиса в k-м полуцикле нагружения.
Зависимость ширины петли гистерезиса от числа полуциклов нагружения
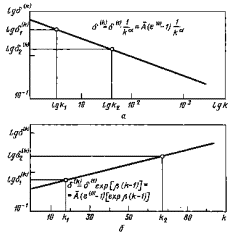
а - циклическое упрочнение; б - циклическое разупрочнение
Для расчетов в заданном диапазоне максимальных деформаций рекомендуется применять средние коэффициенты α и β, полученные при различных значениях исходных деформаций в заданном диапазоне.
5.5. Определение располагаемой пластичности материала
5.5.1. Располагаемую пластичность материала (εf )определяют как
![]() , (64)
, (64)
|
где ΨB и Ψ |
- коэффициенты уменьшения поперечного сечения, соответствующие достижению предела прочности или разрыву образца. Определяют по ГОСТ 1497. |
5.6. Определение кривой малоцикловой усталости
5.6.1. Кривую малоцикловой усталости определяют экспериментально по результатам испытаний серии образцов при жестком нагружении по ГОСТ 25.502. Результаты представляют в виде зависимости долговечности от циклической упругопластической или пластической деформации.
5.6.2. Аналитически кривую малоцикловой усталости выражают уравнениями:
![]() , (65)
, (65)
, (66)
![]() . (67)
. (67)
При этом зависимость долговечности от
циклической пластической деформации (![]() ) используют в диапазоне чисел циклов < 103 - 5
∙ 103.
) используют в диапазоне чисел циклов < 103 - 5
∙ 103.
Зависимость долговечности от циклических упругопластических деформаций (ε(k) применяют во всем малоцикловом диапазоне чисел циклов нагружения (< 5 ∙ 104 - 105).
Коэффициенты в уравнениях определяют по экспериментальным данным о долговечности при малоцикловом нагружении с симметричным циклом деформаций.
5.6.3. Для приближенных расчетов кривой малоцикловой усталости используют корреляционные зависимости, устанавливающие связь характеристик сопротивления малоцикловой усталости с прочностью и пластичностью материала при статическом разрыве образца. При этом принимают следующие значения коэффициентов уравнений кривой малоцикловой усталости:
![]() ;
;
![]() .
.
Показатель μ доя широкого круга конструкционных сталей и сплавов, в первом приближении, равен 0,5-0,6.
Графики, соответствующие уравнениям (65) - (67) с учетом величин коэффициентов, приведены на черт. 3. Там же даны линии, характеризующие первое и второе слагаемые уравнений (66), (67).
Зависимость долговечности от величины пластической (а)
и упругопластической деформации (б,
в) в цикле при ε(k) = const
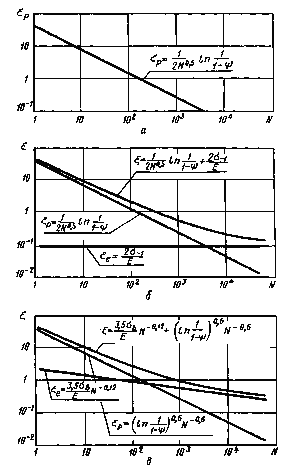
5.6.4. Для получения расчетных кривых используют, с целью обеспечения запасов прочности, минимально гарантированные по техническим условиям на материал величины Ψ, σB , σ-1 . При наличии статистических данных в расчет вводят характеристики, соответствующие средним за вычетом трех стандартных отклонений.
5.6.5. В области числа циклов нагружения до разрушения 104 циклов асимметрию деформаций при определении расчетных кривых малоцикловой усталости не учитывают, если еmах < 0,25εf.
При еmах > 0,25εf, в
уравнениях кривых малоцикловой усталости используют коэффициенты, равные ![]() и
и ![]() .
.
При числе циклов нагружения в диапазоне 104-105 асимметрию цикла нагружения учитывают способом, аналогичным применяемому в многоцикловой области.
5.6.6. Масштабный эффект, влияние чистоты поверхности, коррозии и т.п. следует оценивать постановкой соответствующих экспериментов.
ПРИЛОЖЕНИЕ
1
Обязательное
ОБОЗНАЧЕНИЯ, ПРИМЕНЯЕМЫЕ В СТАНДАРТЕ
|
σ-1 |
- предел выносливости при симметричном цикле гладких лабораторных образцов диаметром d0 = 7,5 мм при изгибе с вращением, изготовленных по ГОСТ 25.502, МПа. |
|
|
- медианное значение σ-1 для образцов из металла одной плавки, МПа. |
|
|
- медианное значение предела выносливости на совокупности всех плавок металла данной марки гладких лабораторных образцов диаметром d0 = 7,5 мм, изготовленных из заготовок диаметром d, равным абсолютному размеру рассчитываемой детали, МПа. |
|
К |
- коэффициент снижения предела выносливости. |
|
σ-1Д |
- предел выносливости детали при симметричном цикле, выраженный в номинальных напряжениях, МПа. |
|
|
- медианное значение σ-1Д, МПа. |
|
|
- медианное значение предела выносливости детали на совокупности всех плавок металла данной марки, МПа. |
|
(σ-1)Р |
- значение σ-1 , соответствующее вероятности разрушения Р %, например (σ-1)10 при Р =10 %, МПа. |
|
(σ-1Д)Р |
- предел выносливости детали, соответствующий вероятности разрушения Р %, МПа. |
|
|
- медианное значение предела выносливости гладких лабораторных образцов диаметром d0 = 7,5 мм, изготовленных из заготовок металла данной марки размерами 10-20 мм, МПа. |
|
К1 |
- коэффициент, учитывающий снижение механических свойств металла (σв, σт, σ-1) с ростом размеров заготовок. |
|
σв |
- временное сопротивление (предел прочности) стали данной марки при растяжении, МПа. |
|
|
- медианное значение предела прочности стали данной марки, определенное на образцах, изготовленных из заготовок диаметром d, равным абсолютному размеру рассчитываемой детали, МПа. |
|
Kσ = σ-1d/σ-1д |
- эффективный коэффициент концентрации напряжений. |
|
Кdσ = σ-1d/ σ-1 |
- коэффициент влияния абсолютных размеров поперечного сечения. |
|
σ-1d |
- предел выносливости образца без концентрации напряжений диаметром d, МПа. |
|
|
- коэффициент влияния шероховатости поверхности, равный отношению предела выносливости образца с данным качеством поверхности σ-1f к пределу выносливости гладкого лабораторного образца. |
|
|
- коэффициент влияния поверхностного упрочнения, равный отношению предела выносливости упрочненной детали σ-1Д упр к пределу выносливости неупрочненной детали σ -1д. |
|
КА |
- коэффициент анизотропии. |
|
|
- коэффициент влияния коррозии, равный отношению предела выносливости гладкого образца в условиях коррозии σ-1 кор к пределу выносливости образца при испытаниях в воздухе. |
|
ξ', ξ" |
- поправочные коэффициенты. |
|
vσ |
- постоянная для данного металла величина (при определенной температуре и частоте испытания), определяющая чувствительность к концентрации напряжений и влиянию абсолютных размеров поперечного сечения при изгибе или растяжении-сжатии. |
|
L |
- параметр рабочего сечения образца или детали или его часть, прилегающая к местам повышенной напряженности, мм. |
|
|
- относительный градиент первого главного напряжения в зоне концентрации напряжений, мм-1. |
|
|
- относительный градиент касательного напряжения, мм-1. |
|
L/ |
- критерий подобия усталостного разрушения детали, мм2. |
|
(L/ |
- критерий подобия усталостного разрушения образца диаметром d0 = 7,5 мм, мм2. |
|
|
- относительный критерий подобия усталостного разрушения. |
|
ασ = σmax/σH |
- теоретический коэффициент концентрации напряжений, равный отношению максимального напряжения в зоне концентрации σmax к номинальному напряжению σH, вычисленному по формулам сопротивления материалов (в предположении упругого распределения напряжений). |
|
n = f( |
- коэффициент, зависящий от значений относительного градиента напряжений и предела текучести. |
|
σT |
- предел текучести стали данной марки при растяжении, МПа. |
|
q |
- коэффициент чувствительности металла к концентрации напряжений. |
|
|
- предел выносливости образцов при растяжении-сжатии, МПа. |
|
А, В, С, Z |
- постоянные коэффициенты. |
|
|
- коэффициент вариации пределов выносливости деталей. |
|
Zp |
- квантиль нормального распределения, соответствующая заданной вероятности разрушения Р. |
|
|
- среднее квадратическое отклонение предела выносливости детали, МПа. |
|
|
- коэффициент вариации максимальных разрушающих напряжений в зоне концентрации. |
|
|
- коэффициент вариации средних значений пределов выносливости образцов. |
|
|
- коэффициент вариации теоретического коэффициента концентрации напряжений ασ. |
|
т |
- показатель наклона левой ветви кривой усталости в двойных логарифмических координатах. |
|
NG |
- абсцисса точки перелома кривой усталости. |
|
Ψσ |
- коэффициент чувствительности к асимметрии цикла напряжений. |
|
|
- коэффициент чувствительности к асимметрии цикла напряжений для детали. |
|
σад |
- предельная амплитуда для детали при асимметричном цикле нагружения. |
|
d0, d, dp, D, ρ , t, a, h, H |
- размеры рабочего сечения образцов (деталей), мм. |
|
εf |
- располагаемая пластичность материала, %. |
|
N |
- число циклов нагружения. |
|
k |
- число полуциклов нагружения (k = 0, 1, 2, 3 ... ). |
|
|
- действительное максимальное напряжение в исходном нагружении (нулевой полуцикл), МПа. |
|
σH |
- номинальное напряжение, МПа. |
|
|
- коэффициент концентрации напряжений в упругопластической области в исходном нагружении (нулевой полуцикл). |
|
|
- действительная максимальная упругопластическая деформация в исходном нагружении (нулевой полуцикл), %. |
|
еH |
- номинальная деформация в исходном нагружении (нулевой полуцикл), %. |
|
|
- коэффициент концентрации деформаций в упругопластической области в исходном нагружении (нулевой полуцикл). |
|
|
- действительное максимальное напряжение в k-м полуцикле нагружения, МПа. |
|
SH |
- номинальное напряжение в k-м полуцикле нагружения, МПа. |
|
|
- коэффициент концентрации напряжений в упругопластической области в k-м полуцикле нагружения. |
|
|
- действительная максимальная упругопластическая деформация в k-м полуцикле нагружения, |
|
εH |
- номинальная деформация в k-м полуцикле нагружения, %. |
|
|
- коэффициент концентрации деформаций в упругопластической области в k-м полуцикле нагружения. |
|
e(0) |
- уровень деформации в исходном нагружении гладких образцов, %. |
|
σ(0) |
- уровень напряжений в исходном нагружении гладких образцов, МПа. |
|
|
- предел пропорциональности в исходном нагружении, определенный при допуске на пластическую деформацию 0,02 % в координатах σ - е, МПа. |
|
|
- деформация, соответствующая пределу пропорциональности в исходном нагружении в координатах σ - е, %. |
|
|
- предел пропорциональности в k-м полуцикле нагружения в координатах S - ε, МПа. |
|
|
- деформация, соответствующая пределу пропорциональности в k-м полуцикле нагружения в координатах S - ε, %. |
|
|
- показатель упрочнения в упругопластической области при линейной аппроксимации диаграммы статического деформирования. |
|
|
- показатель упрочнения в упругопластической области при линейной аппроксимации диаграммы циклического деформирования в k-м полуцикле нагружения. |
|
т(0) |
- показатель упрочнения в упругопластической области при степенной аппроксимации диаграммы статического деформирования. |
|
m(k) |
- показатель упрочнения в упругопластической области при степенной аппроксимации диаграммы циклического деформирования в k-м полуцикле нагружения. |
|
δ(1) |
- ширина петли гистерезиса в 1-м полуцикле нагружения, %. |
|
δ(k) |
- ширина петли гистерезиса в k-м полуцикле нагружения, %. |
|
e(k) |
- упругопластическая деформация, накопленная после k-го полуцикла нагружения, %. |
|
|
- пластическая деформация, накопленная после k-го полуцикла нагружения, %. |
|
|
- максимальная упругопластическая деформация, накопленная за k полуциклов нагружения, |
|
|
- размах упругопластической деформации в k-м полуцикле нагружения, %. |
|
|
- размах пластической деформации в k-м полуцикле нагружения, равный σ(k). |
|
|
- упругая деформация в k-м полуцикле нагружения, %, равная S(k)/Е. |
|
Ψ |
- относительное сужение площади поперечного сечения образца при статическом растяжении, %. |
|
ΨB |
- относительное сужение площади поперечного сечения образца, соответствующее σв, %. |
|
Е |
- модуль упругости материала, МПа. |
|
|
- коэффициенты уравнений кривой малоцикловой усталости. |
Примечание. При кручении обозначения аналогичны с заменой σ на τ, например τ-1? τ-1д и т.д.
ПРИЛОЖЕНИЕ 2
Обязательное
ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНЫХ КОЭФФИЦИЕНТОВ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ Кσ Кτ ОТНОШЕНИЙ 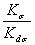 ,
, 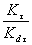 , КОЭФФИЦИЕНТОВ n, q, К1,
И К3
, КОЭФФИЦИЕНТОВ n, q, К1,
И К3
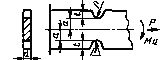
Валы с напрессованными деталями при изгибе
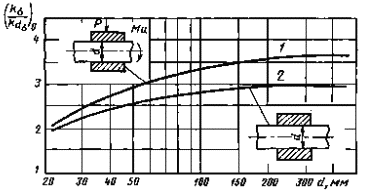
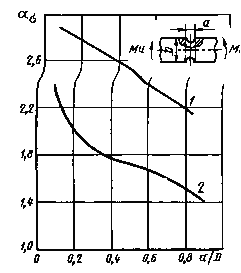
σв = 500 МПа; Р ≥ 30 МПа; 1 - через напрессованную деталь передается сила или момент; 2 - через напрессованную деталь не передается усилий
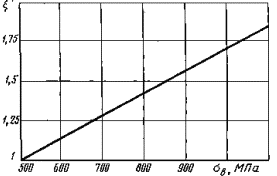
Поправочный коэффициент ![]() на предел прочности σB (к черт. 1)
на предел прочности σB (к черт. 1)
Черт. 2
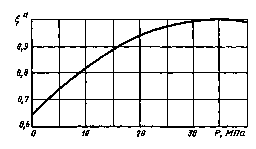
Поправочный коэффициент ![]() на давление
напрессовки Р (к черт. 1)
на давление
напрессовки Р (к черт. 1)
Черт. 3
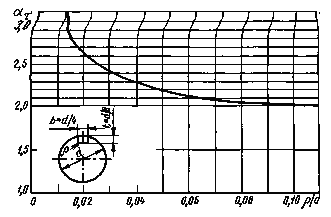
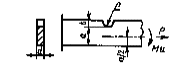
Валы с поперечным отверстием при изгибе
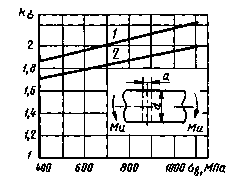
![]() = 0,05-0,10; 2 -
= 0,05-0,10; 2 - ![]() = 0,15-0,25;
= 0,15-0,25;
![]()
при d = 30-50 мм
Черт. 4
Валы с поперечным отверстием при кручении
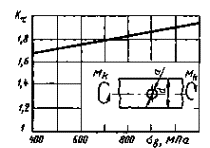
![]() = 0,05 - 0,25;
= 0,05 - 0,25;
при d = 30-50 мм
Черт. 5
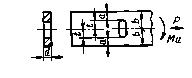
Валы с поперечным отверстием при растяжении-сжатии
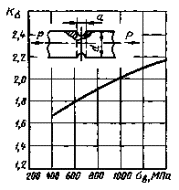
![]() = 0,20-0,45; d = 15 мм;
= 0,20-0,45; d = 15 мм; 
Черт. 6
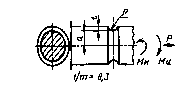
Валы с V-образной кольцевой выточкой
1 -
прямобочные и эвольвентные шлицы;
2 - прямобочные шлицы; 3 - эвольвентные шлицы
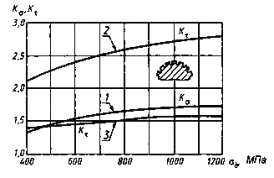
Коэффициенты Кσ, Кτ для валов со шпоночными пазами типов А и В
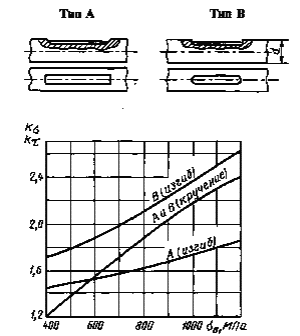
Черт. 13*
* Черт. 8-12. (Исключены, Изм. № 1)
Коэффициенты n
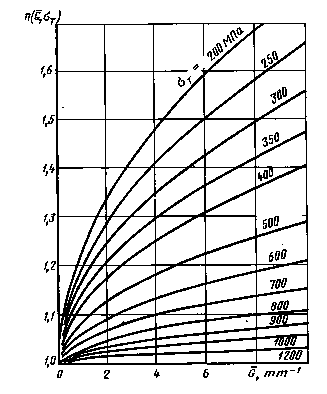
Коэффициенты q
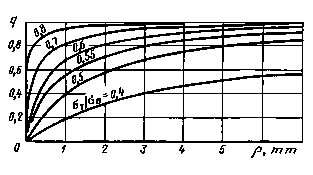
Коэффициенты К1
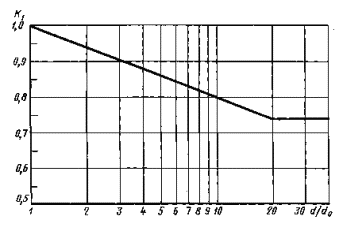
ПРИЛОЖЕНИЕ 3
Обязательное
ОПРЕДЕЛЕНИЕ ТЕОРЕТИЧЕСКИХ КОЭФФИЦИЕНТОВ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ ασ, ατ
Пластины с двухсторонним надрезом при растяжении (черт. 1-3)
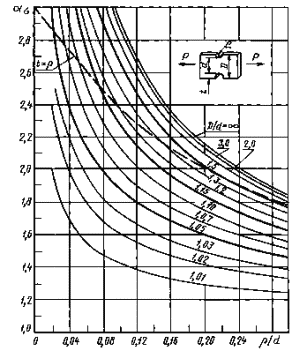
Пунктирная
линия t = ρ -
полуокружность;![]() = 0,02-0,30
= 0,02-0,30
0,001 ≤ ρ/D ≤ 0,050
Черт. 2
0,05 ≤ ρ/D ≤ 1,00
Формулы к черт. 1-3
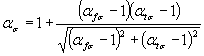
где ![]() ;
;
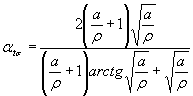
![]()
Пластины типов а и в при растяжении
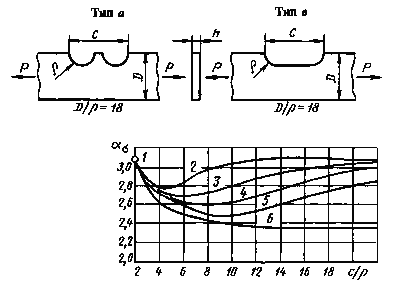
1-5 - пластины типа а (1 - однократный надрез; 2 - двухкратный надрез; 3 - трехкратный надрез; 4 - четырехкратный надрез; 5 - пятикратный надрез); 6 - пластины типа в
![]()
Черт. 4
Коэффициент разгрузки γ
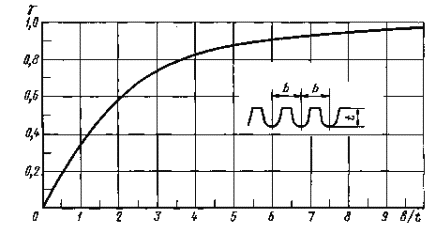
Черт. 5
Примечание. Коэффициент у для многократного надреза находят по диаграммам для однократного надреза при глубине t' = γ ∙ t, где t - глубина многократного надреза, t'- глубина эквивалентного однократного надреза.
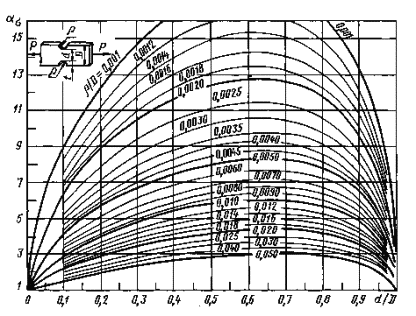
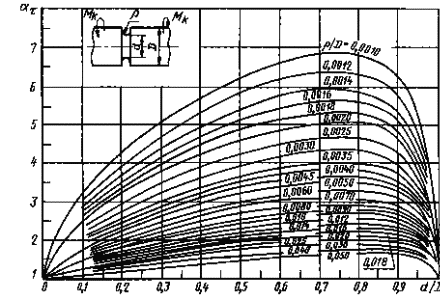
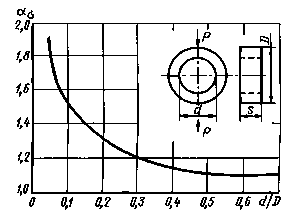
Валы с выточкой при растяжении (черт. 6-8)
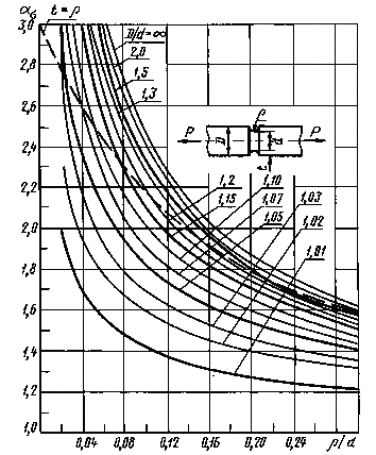
ρ/d = 0,02 - 0,30
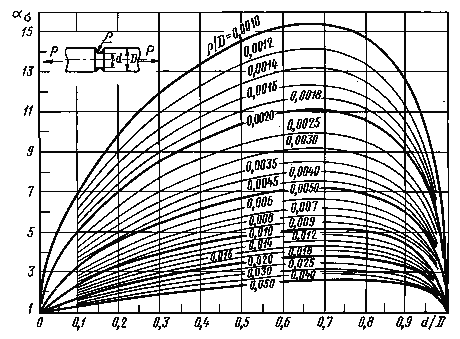
0,001 < ρ/D< 0,050
Черт. 7
0,050 ≤ ρ/D ≤ 1,00
Формулы к черт. 6-8
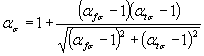
где ![]() ,
,
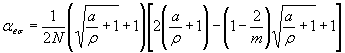 ,
,
![]() ,
,
![]() ,
, ![]() .
.
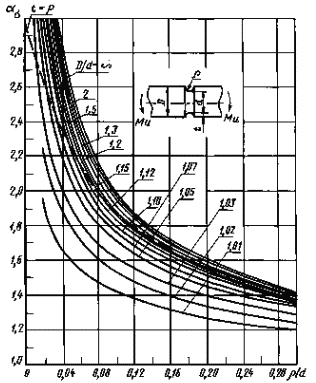
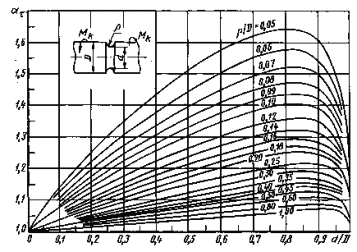
Пластины с двусторонним надрезом при изгибе (черт. 9-11)
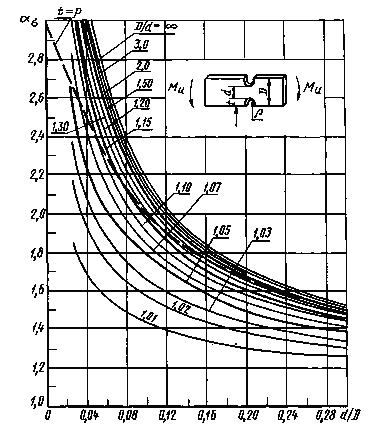
ρ/d = 0,02-0,30
0,001 ≤ ρ/D ≤ 0,050
Черт. 10
0,050 ≤ ρ/D ≤ 1,00
Формулы к черт. 9-11
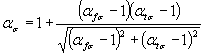
где ![]() ,
,
|
|
Влияние угла надреза на коэффициент концентрации напряжений при изгибе пластины с односторонним надрезом
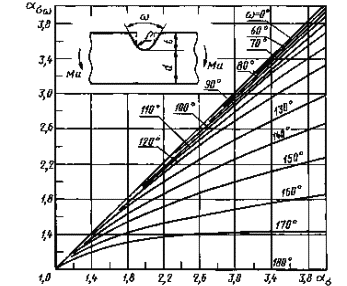
ασ - коэффициент
концентрации напряжений для надреза с углом ω
= 0 (пунктир на схеме пластины); ![]() - коэфффициент
концентрации напряжений для надреза с углом ω
при тех же размерах
- коэфффициент
концентрации напряжений для надреза с углом ω
при тех же размерах
Черт. 12
Тонкий лист с двухсторонним надрезом при изгибе в плоскости, перпендикулярной плоскости листа (t/h значительно)
Черт. 13
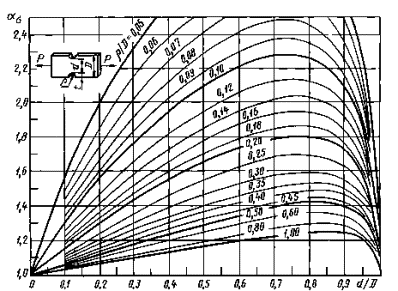
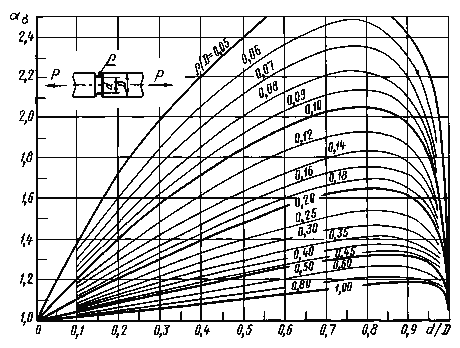
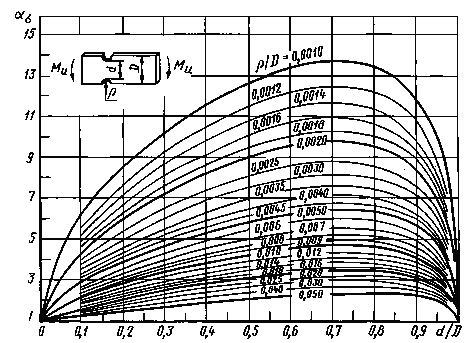
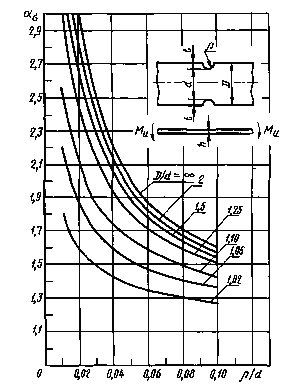
Валы с выточкой при изгибе (черт. 14-16)
ρ/d = 0,02-0,30
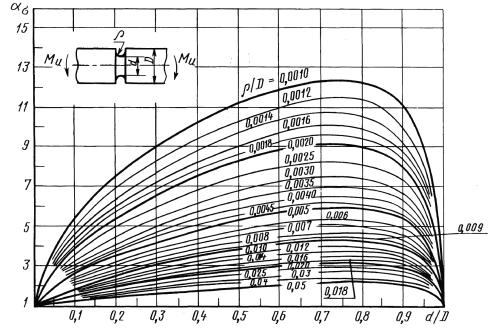
0,001 ≤ ρ/D ≤ 0,050
Черт. 15
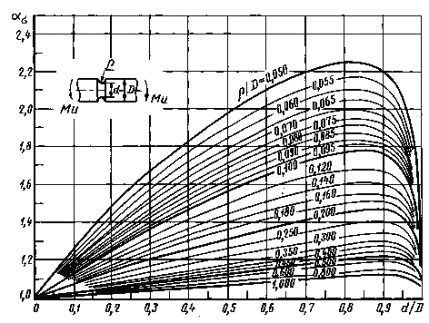
0,050 ≤ ρ/D ≤ 1,00
Формулы к черт. 14-16
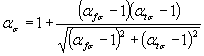
где ![]() ,
,
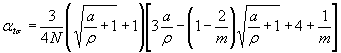 ,
,
|
|
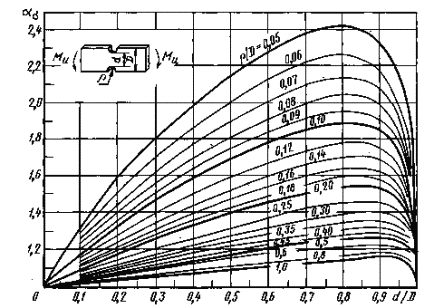
Валы с выточкой при кручении (черт. 17-19)
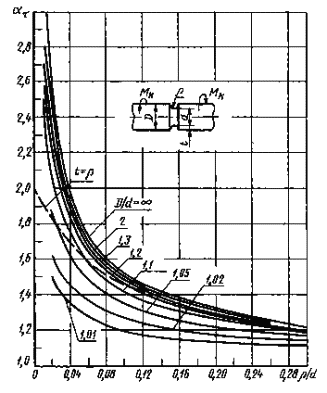
ρ/d = 0,02 - 0,30
0,001 ≤ ρ/D ≤ 0,050
0,05 ≤ ρ/D ≤ 1,00
Формулы к черт. 17-19
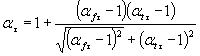
где ![]() ,
,
|
|
Симметричная
ступенчатая пластина с галтелями при растяжении
(по данным поляризационно-оптических измерений)
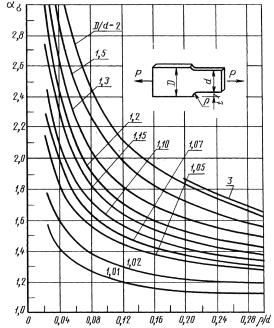
|
|
Ступенчатый вал с галтелью при растяжении (сжатии)
|
|
Черт. 21
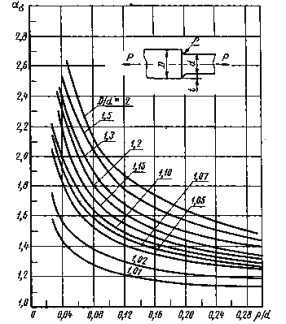
Ступенчатая пластина с галтелями при изгибе (по данным поляризационно-оптических измерений)
|
|
Влияние длины выступа пластины на коэффициент концентрации напряжений для ступенчатой пластины с галтелями при изгибе (черт. 23-25)
D/d = 1,25
Черт. 23
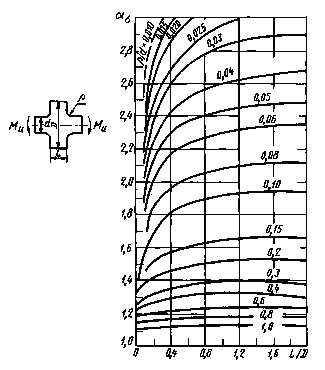
D/d = 2
Черт. 24
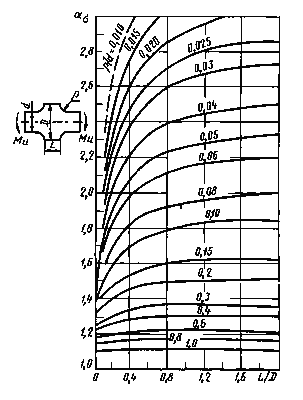
D/d = 3
Ступенчатая пластина с эллиптической галтелью при изгибе
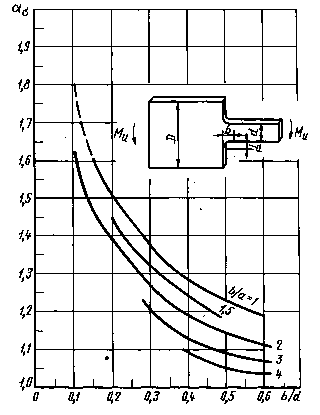
D/d = 3 (по данным поляризационно-оптических измерений)
Черт. 26
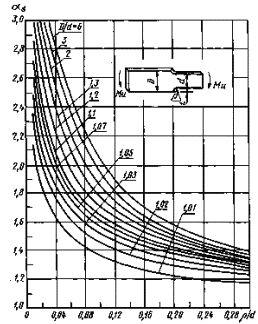
Ступенчатый вал с галтелью при изгибе
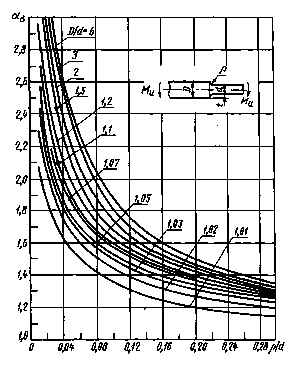
|
|
Ступенчатый вал с галтелью при кручении (измерения по методу электрических аналогий)
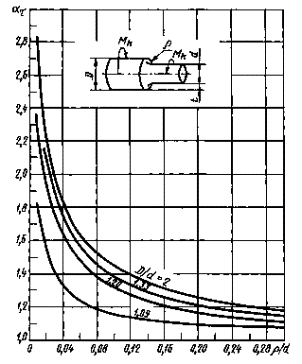
|
|
Тонкая пластина ограниченной ширины с поперечным отверстием при растяжении (теоретическое решение)
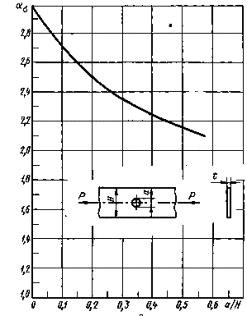
![]()
Тонкая пластина неограниченной ширины с поперечным отверстием при изгибе (теоретическое решение)
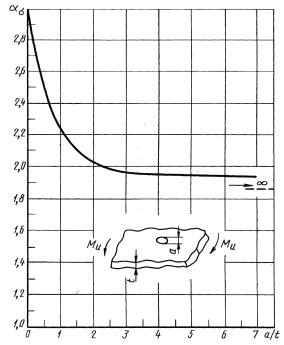
Черт. 30
Тонкая пластина ограниченной ширины с поперечным отверстием при изгибе
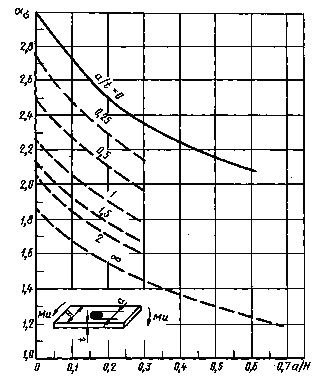
![]()
Черт. 31
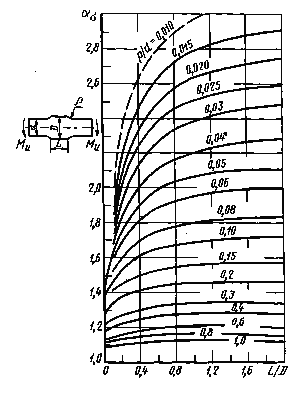
Вал с поперечным отверстием при изгибе (измерения с помощью тензометров)
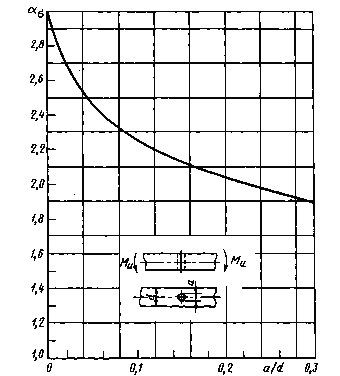
|
|
Черт. 32
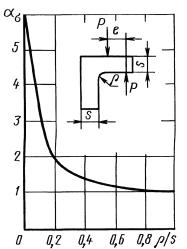
Пластины с Т-образной головкой
![]() (черт. 33-37)
(черт. 33-37)
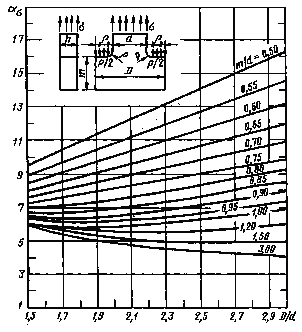
ρ/d =0,050 (измерения с помощью поляризационно-оптического метода)
Черт. 33
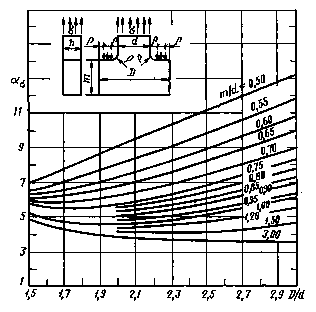
ρ/d = 0,075
Черт. 34
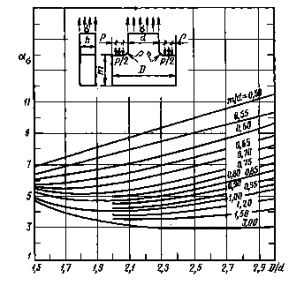
ρ/d =0,1
Черт. 35
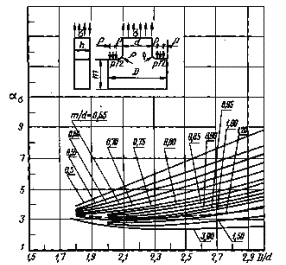
ρ/d =0,2
Черт. 36
Примечание. Координата точки приложения сосредоточенной силы Р/2 по оси X-переменная
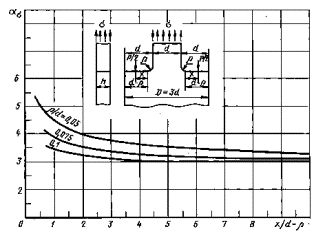
Пластина с поперечной прорезью при изгибе
Черт. 38
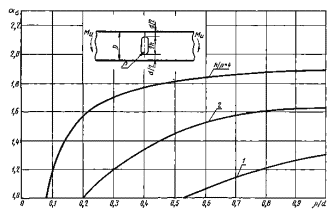
Пластина с поперечной прорезью при растяжении
![]() .
.
![]() .
.
Черт. 39
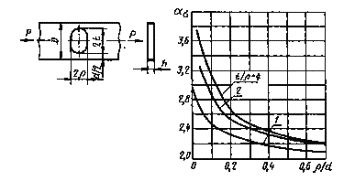
Пластина с односторонним надрезом при изгибе
|
|
Черт. 40
Пластина с эксцентрично расположенным отверстием толщиной h при растяжении
![]() .
.
Черт. 41
Вал с поперечным отверстием при растяжении(1) и изгибе (2)
Черт. 42
Вал с пазом для призматической шпонки при кручении
Черт. 43
Кольцо с наружной единичной нагрузкой Р
![]() .
.
Черт. 44
Уголок с равными по толщине полками при изгибающем моменте Р ∙ е
Черт. 45
Уголок с неравными по толщине полками при изгибе от единичной нагрузки Р
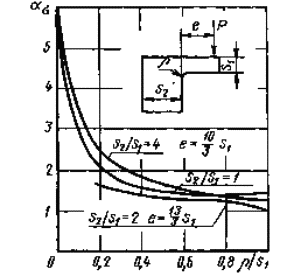
Черт. 46
Уголок с приблизительно равными по толщине полками при изгибе от единичной нагрузки Р
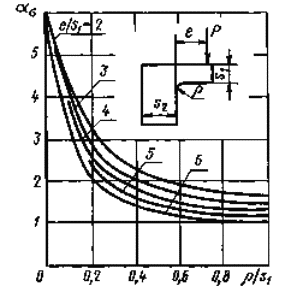
Номограмма для определения теоретического коэффициента концентрации
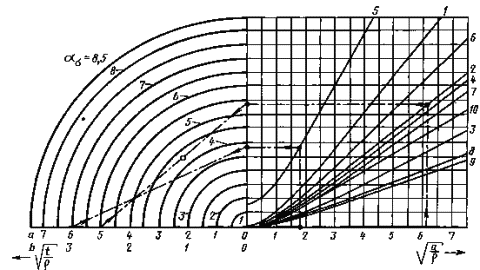
Номограмма для кольцевых выточек с осевым отверстием
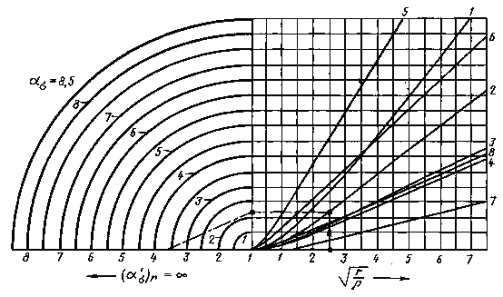
ПРИЛОЖЕНИЯ 1-3. (Измененная редакция, Изм. № 1).
ПРИЛОЖЕНИЕ 4
Обязательное
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ФУНКЦИИ F (Θ , v), ПАРАМЕТРА L,
КОЭФФИЦИЕНТА ВЛИЯНИЯ ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ КF И КОЭФФИЦИЕНТА Ккор
Значения функции F (Θ , v)
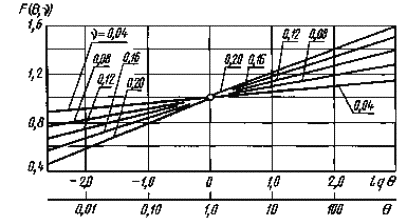
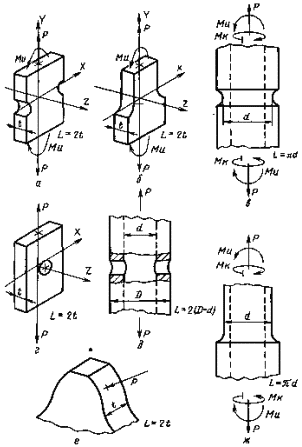
Схемы к определению параметра L
Значения коэффициентов KF
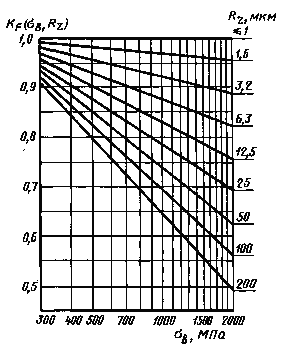
Примечание. При наличии окалины используют нижнюю прямую (Rz = 200 мкм).
Влияние коррозии до испытания на усталость на предел выносливости стальных образцов (при изгибе с вращением на базе 107 циклов при частоте нагружения 30-50 Гц)
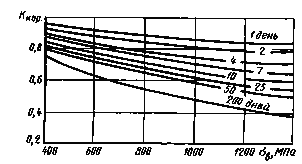
Влияние коррозии в процессе испытания на предел выносливости стальных образцов при изгибе с вращением (осредненные кривые) на базе 107 циклов при частоте нагружения 30-50 Гц
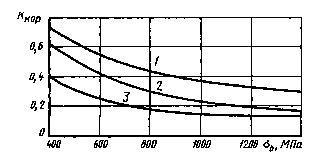
1 - пресная вода (наличие концентрации напряжений); 2 - пресная вода (отсутствие концентрации напряжений); 3 - морская вода (отсутствие концентрации напряжений)
ПРИЛОЖЕНИЕ
5
Рекомендуемое
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ВЛИЯНИЯ ПОВЕРХНОСТНОГО УПРОЧНЕНИЯ Kv
1. Коэффициенты влияния поверхностного упрочнения на предел выносливости вычисляют по формуле
![]() , (1)
, (1)
|
где σ-1Дупр |
- предел выносливости упрочненных деталей; |
|
σ-1Д |
- предел выносливости неупрочненных деталей. |
Средние значения KV для различных методов поверхностного упрочнения образцов из углеродистых и легированных конструкционных сталей приведены в табл. 1-3.
Таблица 1
Влияние поверхностной закалки токами высокой частоты
(изгиб с вращением, глубина закаленного слоя 0,9-
|
Вид образца |
КV для образца диаметром |
|
|
7- |
30- |
|
|
Без концентрации напряжений |
1,3-1,6 |
1,2-1,5 |
|
С концентрацией напряжений |
1,6-2,8 |
1,5-2,5 |
Таблица 2
Влияние химико-термической обработки
|
Характеристика химико-термической обработки |
Вид образца |
КV для образцов диаметром |
||
|
8- |
|
30- |
||
|
Азотирование при глубине слоя 0,1- |
Без концентрации напряжений |
1,15-1,25 |
- |
1,10-1,15 |
|
С концентрацией напряжений (поперечное, отверстие, надрез) |
1,90-3,00 |
1,30-2,00 |
||
|
Цементация при
глубине слоя 0,2- |
Без концентрации напряжений |
1,20-2,10 |
1,10-1,50 |
|
|
С концентрацией напряжений |
1,50-2,50 |
1,20-2,00 |
||
|
Цианирование при глубине слоя |
Без концентрации напряжений |
- |
1,80 |
- |
Таблица 3
Влияние поверхностного наклепа
|
Способ обработки |
Вид образца |
КV для образца диаметром |
|
|
7- |
30- |
||
|
Обкатка роликом |
Без концентрации напряжений |
1,20-1,40 |
1,10-1,25 |
|
С концентрацией напряжений |
1,50-2,20 |
1,30-1,80 |
|
|
Обдувка дробью |
Без концентрации напряжений |
1,10-1,30 |
1,10-1,20 |
|
С концентрацией напряжений |
1,40-2,50 |
1,10-1,50 |
|
2. Приведенные в п. 1 значения КV соответствуют оптимальной технологии упрочнения и отсутствию технологических дефектов. При неправильной технологии упрочнения или наличии дефектов (обрыв поверхностного закаленного слоя в зоне концентрации напряжений, обезуглероживание поверхностного слоя, шлифовочные прижоги и другие дефекты) может получиться не повышение, а даже снижение пределов выносливости.
Поэтому введение в формулу (2) (см. п. 1.1) коэффициентов KV возможно только при проведении исследований для обоснования технологических режимов упрочнения применительно к конкретной детали и при получении стабильного эффекта упрочнения (в смысле повышения предела выносливости) в условиях производства.
ПРИЛОЖЕНИЕ 6
Справочное
ПРИМЕРЫ РАСЧЕТА ХАРАКТЕРИСТИК СОПРОТИВЛЕНИЯ УСТАЛОСТИ ДЕТАЛЕЙ МАШИН
Пример 1.
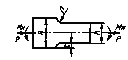
Определить среднее значение и коэффициент вариации предела выносливости вала при изгибе с вращением в месте перехода одного сечения к другому по галтели, показанного на черт. 1.
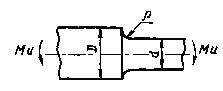
D =
Черт 1
Вал изготовлен из стали 45, σв = 650 МПа.
Дано: ![]() = 300 МПа;
= 300 МПа; ![]() = 0,07; поверхностному упрочнению вал не
подвергается. Вал изготовлен тонкой обточкой (Rz
= 0,07; поверхностному упрочнению вал не
подвергается. Вал изготовлен тонкой обточкой (Rz ![]() 6,3 мкм).
6,3 мкм).
Находим значение ασ по черт. 27 приложения 3.
Для ![]()
2. Определяем значение ![]() по формуле табл. 1 настоящего стандарта
по формуле табл. 1 настоящего стандарта
![]() ;
;
![]() ;
;
![]() .
.
3. Вычисляем значение Θ.
L = πd =314 мм - при изгибе с вращением круглого вала;
![]()
4. Для стали 45 можно принять vσ = 0,211-0,000143 ∙ 650 = 0,12. По табл. 4 или по черт. 1 (приложение 4) находим при Θ = 12,35; F(Θ , vσ) = 1,15.
5. Определяем Kσ/Kdσ по формуле (11) настоящего стандарта
![]() = ασ ∙
F(Θ
, vσ) = 1,62 - 1,15 =
1,86.
= ασ ∙
F(Θ
, vσ) = 1,62 - 1,15 =
1,86.
4, 5. (Измененная редакция, Изм. № 1).
6. Для случая тонкой обточки (Rz = 6,3 мкм) по черт. 3 (приложения 4) для σв = 650 МПа находим: KF = 0,91.
7. Определяем значение К по формуле (2) настоящего стандарта
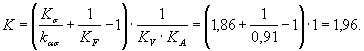
(Измененная редакция, Изм. № 1).
8. Коэффициент анизотропии КА= 1, KV= 1.
9. Коэффициент К1 = 1.
(Измененная редакция, Изм. № 1).
10. (Исключен, Изм. № 1).
11. Среднее значение предела выносливости вала составит:
![]()
Коэффициент вариации ![]() находим по формуле (38) настоящего стандарта
находим по формуле (38) настоящего стандарта
![]()
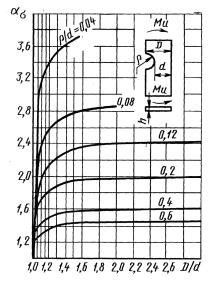
Для подсчета коэффициента вариации ![]() находим по черт. 27 (приложения 3) значения ασ при D/d = 1,2 и двух значениях, близких к 0,1, например при
находим по черт. 27 (приложения 3) значения ασ при D/d = 1,2 и двух значениях, близких к 0,1, например при
(ρ/d)1 = 0,09, ![]() = l,67,
(ρ/d)2 =0,11,
= l,67,
(ρ/d)2 =0,11, ![]() = 1,59.
= 1,59.
По формуле (44) настоящего стандарта находим
![]()
откуда ασ = 2,03-4 ∙ ρ/d.
По формуле (43) настоящего стандарта получаем
![]()
Принимая отклонения радиуса ±
![]()
Из-за отсутствия данных коэффициент
вариации ![]() принимаем равным
принимаем равным
![]()
Общий коэффициент вариации предела выносливости вала составит
![]()
(Измененная редакция, Изм. № 1).
Пример 2.
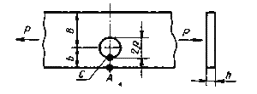
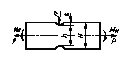
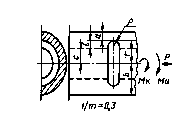
Определить среднее значение предела выносливости пластины с отверстием при растяжении-сжатии, показанной на черт. 2.
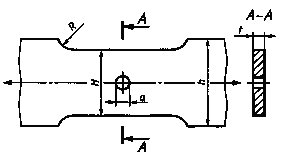
Н =
Черт. 2
Пластина изготовлена из стали марки Ст.3. Rz = 50 мкм.
![]() = 402 МПа;
= 402 МПа; ![]() = 185 МПа;
= 185 МПа; ![]() = 0,06;
= 0,06; ![]() = 270 МПа.
= 270 МПа.
(Измененная редакция, Изм. № 1).
1. Определяем значение ασ на черт. 29 (приложения 3)
Для ![]() ; ασ
=2,73.
; ασ
=2,73.
2. Определяем значение ![]() по формуле табл. 1 настоящего стандарта
по формуле табл. 1 настоящего стандарта
![]() .
.
3. Находим коэффициент n по черт. 14 (приложения 2)
n = 1,12.
4. Определяем коэффициент Кσ по формуле (13) настоящего стандарта
![]()
5. Определяем параметр vσ по формуле (27) настоящего стандарта vσ = 0,211 - 0,000143 ∙ 402 = 0,15.
(Измененная редакция, Изм. № 1).
5а. Определяем значения L, ![]() и ΘГЛ для аналогичной пластины без концентратора напряжений
по табл. 1 и приложению 4 (черт. 2) настоящего стандарта
и ΘГЛ для аналогичной пластины без концентратора напряжений
по табл. 1 и приложению 4 (черт. 2) настоящего стандарта
L = 2t = 2 ∙ 12 =
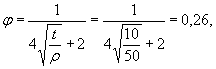
![]()
![]()
(Введен дополнительно, Изм. № 1).
6. Определяем коэффициент Кdσ по формуле (12) настоящего стандарта
Kdσ = 0,5(1 +![]() ) = 0,5(1 + 55-0,15) = 0,77,
) = 0,5(1 + 55-0,15) = 0,77,
![]()
(Измененная редакция, Изм. № 1).
По черт. 3 (приложение 4) находим KF= 0,89.
Коэффициент K определяем по формуле (2) настоящего стандарта
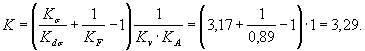
(Измененная редакция, Изм. № 1).
9. 10. (Исключены, Изм. № 1).
11. Средний предел выносливости пластины с отверстием вычисляем по формуле (1) настоящего стандарта (коэффициент К1 = 1 для углеродистых сталей)
![]()
(Измененная редакция, Изм. № 1).
Пример 3.
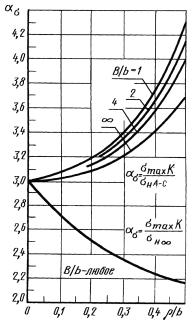
Определить среднее значение предела выносливости вала с канавкой при кручении (черт. 3).
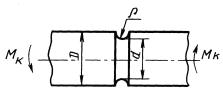
D =200 мм; d = 180 мм; ρ = (1,8 ± 0,3) мм.
Черт. 3
Вал изготовлен из стали марки 40ХН. σв = 820 МПа, σт = 650 МПа, ![]() = 240 МПа,
= 240 МПа, ![]() = 0,07; канавку
изготовляют тонкой обточкой и поверхностному упрочнению не подвергают (Rz = 6,3 мкм).
= 0,07; канавку
изготовляют тонкой обточкой и поверхностному упрочнению не подвергают (Rz = 6,3 мкм).
1. Находим значение ατ по черт. 18 (приложения 3) при
![]()
2. Определяем значение q по черт. 15 (приложения 2)
q = 0,96.
3. Величину Кτ определяем по формуле (19) настоящего стандарта
Кτ = 1 + q(ατ - 1) = 1+ 0,96(2,6-1) = 2,54.
4. Для d =
5. Определяем параметры vσ и vτ по формулам (27) и (28) настоящего стандарта:
vσ = 0,211 - 0,000143 ∙ 820 = 0,09,
vτ = 1,5 - 0,09 = 0,140.
(Измененная редакция, Изм. № 1).
5.1. Определяем значение Θгл по п. 1.2.3.1 настоящего стандарта
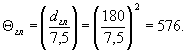
5.2. Вычисляем коэффициент Кdτ по формуле (12) настоящего стандарта
Кdτ = 0,5(1 + ![]() ) = 0,5(1 + 576-0,14) = 0,71.
) = 0,5(1 + 576-0,14) = 0,71.
5.3. Определяем отношение ![]()
![]()
5.1-5.3. (Введены дополнительно, Изм. № 1).
6. Из черт. 3 (приложения 4) определяем коэффициент KF для тонкой обточки (Rz = 6,3 мкм)
KF=0,89.
7. При отсутствии поверхностного упрочнения
KV = 1
8. При кручении КА = 1 (см. п. 1.11.2).
9. Коэффициент К равен
К = (3,58+![]() =3,7.
=3,7.
(Измененная редакция, Изм. № 1).
10. Принимаем коэффициент К1 для d =
11. Вычисляем предел выносливости материала заготовки по формуле (6) настоящего стандарта
![]() = 0,74 ∙ 240 = 178 МПа.
= 0,74 ∙ 240 = 178 МПа.
12. Вычисляем средний предел выносливости вала по формуле (4) настоящего стандарта
![]()
(Измененная редакция, Изм. № 1).
ПРИЛОЖЕНИЕ 7
Справочное
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАНДАРТА
Настоящий стандарт является унифицированным стандартом СССР и ГДР, разработанным по плану унификации стандартов двух стран.
В основу стандарта положены методы оценки пределов выносливости и других характеристик сопротивления усталости деталей, вошедшие в стандарты ГДР [1,5-7] и в справочные руководства СССР [2-4].
Излагаются методы оценки медианных
значений пределов выносливости деталей ![]() и их коэффициентов
вариации
и их коэффициентов
вариации ![]() , что позволяет определять значения пределов выносливости (σ-1д)р, соответствующие заданной вероятности Р %.
, что позволяет определять значения пределов выносливости (σ-1д)р, соответствующие заданной вероятности Р %.
Наиболее точным методом определения коэффициентов К, отражающих суммарное влияние всех факторов на пределы выносливости, является экспериментальный метод (п. 1.2.1).
Для расчетного определения эффективных коэффициентов концентрации Кσ, Кτ и отношений Kσ/Kdσ., Kτ/Kdt предлагаются три метода, изложенные в порядке предпочтительного использования, зависящего от имеющейся исходной информации.
Первый метод, изложенный в п. 1.2.3.1, формулы (11), (12), основан на статистической теории подобия усталостного разрушения [4]. Эта теория получила апробирование во многих лабораториях СССР в течение последних 20 лет и успешно используется в ряде отраслей машиностроения. В случае экспериментального определения коэффициентов vσ и vτ путем испытаний на усталость образцов и моделей в статистическом аспекте ошибка в оценке отношений Kσ/Kdσ не превышает 4 % с вероятностью 95 %. При испытаниях по стандартной методике ограниченного числа образцов каждого типоразмера для определения v ошибка не превышает 8 % с вероятностью 95 %.
При затруднениях с определением параметра L, а, следовательно, и критерия подобия Θ, входящего в формулы (11), (12), рекомендуется использовать приближенный метод Зибеля и Штилера, представленный формулами (13), (14), рекомендуемый стандартом ГДР TGL 19340. Для этой же цели допускается применение формул (18), (19), основанных на использовании коэффициентов чувствительности металла к концентрации напряжений q, рекомендуемых в американской справочной литературе /8/, а также в ряде руководств в СССР. Следует иметь в виду, что формулы (13)-(19) приводят к погрешностям существенно большим (до 20 %), чем формулы (11), (12). Формулы (29), (30) для коэффициентов влияния качества обработки поверхности KFσ , KFτ формула (20) для коэффициента влияния абсолютных размеров и формула (15) получены разработчиками стандарта ГДР Б. Хенелем, Г. Виртгеном и К. Шустером (Институт легких конструкций г. Дрезден) путем аппроксимации эмпирических графиков, приведенных в TGL 19340.
В разд. 3 стандарта изложен метод оценки
коэффициентов вариации пределов выносливости ![]() , вытекающий из теории подобия усталостного разрушения [4].
В связи с оценкой коэффициентов
, вытекающий из теории подобия усталостного разрушения [4].
В связи с оценкой коэффициентов ![]() вводят два медианных значения предела
выносливости гладких лабораторных образцов диаметром d0 =
вводят два медианных значения предела
выносливости гладких лабораторных образцов диаметром d0 = ![]() , определенное на образцах металла одной плавки, и
, определенное на образцах металла одной плавки, и ![]() , определенное на множестве всех плавок металла данной марки.
В связи с этим коэффициент вариации
, определенное на множестве всех плавок металла данной марки.
В связи с этим коэффициент вариации ![]() (формулы 35-37) учитывает межплавочный разброс величин
(формулы 35-37) учитывает межплавочный разброс величин ![]() .
.
Известно, что с ростом размеров заготовки
при термообработке снижаются механические свойства металла (σв, σт, σ-1),
определенные на лабораторных образцах малых размеров ([2],
фиг. 41, стр. 129). В связи с этим вводят коэффициент К1 (формула (3)),
равный отношению пределов выносливости ![]() и
и ![]() определенных на
лабораторных образцах диаметром d0 =
определенных на
лабораторных образцах диаметром d0 =
Теоретические коэффициенты концентрации ασ, ατ предлагается определять по номограммам и формулам Нейбера, по графикам, приведенным в работе [8], а также по приближенной формуле (25), заимствованной из TGL 19340. Последнюю формулу используют в случае необходимости вычислений ασ на ЭВМ.
Величины vσ, vτ, являющиеся параметрами уравнения подобия усталостного разрушения [4], характеризуют чувствительность металла к концентрации напряжений и влиянию абсолютных размеров поперечного сечения. С ростом vσ чувствительность к концентрации напряжений уменьшается, а влияние абсолютных размеров на величины пределов выносливости усиливается.
Значения vσ, vτ находят экспериментально по методике, выбирают 4-5 или более типоразмеров образцов с различными значениями критерия подобия усталостного разрушения Θ (так, чтобы диапазон изменения Θ был по возможности наибольшим). Находят пределы выносливости этих образцов, причем предпочтительно методом «лестницы» или «пробит» - методом. По найденным значениям строят зависимость 1g (ξ - 1) от 1g Θ, соответствующую уравнению подобия [4].
1g (ξ - 1) = - vσ ∙ 1g Θ, (1)
где
![]()
Значение ![]() находят путем
предварительного построения зависимости σтах = ασ
∙ σ-1д от 1g Θ
и ее осреднения. По зависимости (1), найденной методом наименьших квадратов, определяют
значение vσ.
находят путем
предварительного построения зависимости σтах = ασ
∙ σ-1д от 1g Θ
и ее осреднения. По зависимости (1), найденной методом наименьших квадратов, определяют
значение vσ.
В случае невозможности проведения экспериментов значения vσ и vτ определяют по корреляционным зависимостям (27) и (28).
Расчетные характеристики для оценки долговечности при малоцикловом нагружении определяют применительно к широко используемому подходу, основывающемуся на учете местных циклических деформаций в конструкциях. Расчет выполняют с привлечением деформационно-кинетических критериев малоцикловой прочности, трактующих достижение предельного состояния в виде критических величин квазистатических и усталостных повреждений и их сумм в линейной форме. Расчет ведут в деформациях (циклических упругопластических и односторонне накопленных).
Учитывают кинетику односторонне накопленных и циклических деформаций в процессе нагружения в максимально напряженных зонах конструкции, а также деформационную способность материала при статическом (квазистатическом) и малоцикловом нагружениях. Первая характеризуется располагаемой пластичностью, вторая - кривой малоцикловой усталости конструкционного материала.
Изменяющиеся от цикла к циклу диаграммы деформирования используют в форме обобщенной диаграммы, отражающей процессы циклического упрочнения, разупрочнения и стабилизации. Указанная обобщенная диаграмма вошла в практику расчетов при малоцикловом нагружении.
Задачу о напряженно-деформированном состоянии элементов конструкций решают расчетным и экспериментальными методами в циклической упругопластической постановке.
Названные подходы систематически изложены в ряде изданий [3, 9-11].
БИБЛИОГРАФИЯ
|
[1] |
|
|
[2] |
Серенсен С.В., Когаев В.П., Шнейдерович P.M. Несущая способность и расчеты на прочность деталей машин. М., Машгиз, 1963, с. 451 |
|
[3] |
Серенсен С.В., Когаев В.П., Шнейдерович P.M. Несущая способность и расчеты на прочность деталей машин. М., «Машиностроение», 1975, с. 488 |
|
[4] |
Когаев В.П. Расчеты на прочность при напряжениях переменных во времени. М., «Машиностроение»,1977 |
|
[5] |
Hanel В., Wirthgen G. Neufassung des DDR - Standards TGL 19330
«Schwingfestigkeit, Begriffe und Zeichen». IfL-Mitt, |
|
[6] |
C. Schuster und C. Wirthgen.
Aufbau und Anwendung der DDR-Standards TGL 19340 (Neufassung)
«Maschinenbauteile, Dauerschwingfestig-keit», IfL-Mitt., |
|
[7] |
|
|
[8] |
Петерсон Р.Е. Концентрация напряжений. М., «Мир», 1977, с. 302 |
|
[9] |
Москвитин В.В. Пластичность при переменных нагружениях. Изд. Моск. университета, 1965, с. 263 |
|
[10] |
Гусенков А.П. Прочность при изотермическом и неизотермическом малоцикловом нагружении. М.,«Наука», 1979, с. 295 |
|
[11] |
Махутов НА. Деформационные критерии разрушения и расчет элементов конструкций на прочность. М., «Машиностроение», 1981, с. 272 |
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН Академией наук СССР, Государственным комитетом СССР по стандартам, Министерством высшего и среднего специального образования СССР, Министерством тракторного и сельскохозяйственного машиностроения
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ ПОСТАНОВЛЕНИЕМ Государственного комитета СССР по стандартам от 18.05.82 № 1972
3. Стандарт унифицирован со стандартами ГДР TGL 19340/03 и TGL 19340/04
4. ВВЕДЕН ВПЕРВЫЕ
5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
|
Обозначение НТД, на который дана ссылка |
Номер пункта, приложения |
|
ГОСТ 23207-78 |
6. Ограничение срока действия снято по протоколу № 3-93 Межгосударственного совета по стандартизации, метрологии и сертификации (ИУС 5-6-93)
7. ИЗДАНИЕ с Изменением №
1, утвержденным в декабре
| Расположен в: |
|---|
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/27316
На эту страницу сайта можно сделать ссылку:
На правах рекламы:
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|


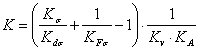
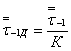
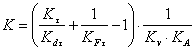
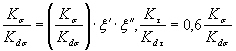
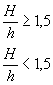
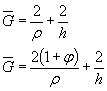
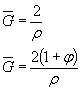
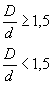
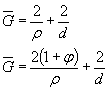
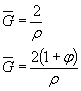
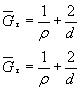
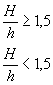
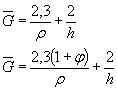
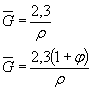
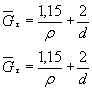
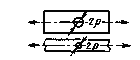
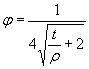
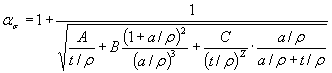
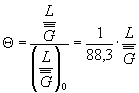
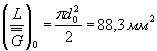
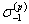
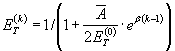
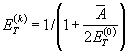
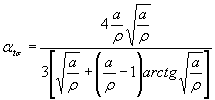
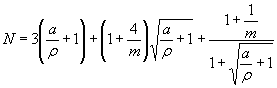
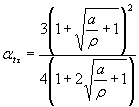 .
.