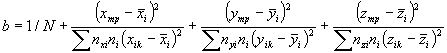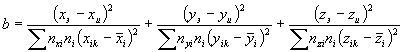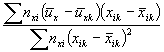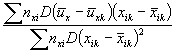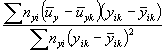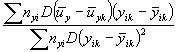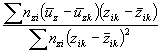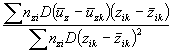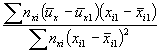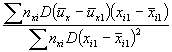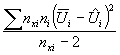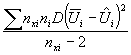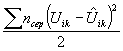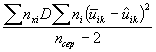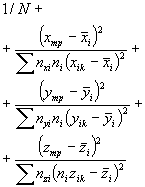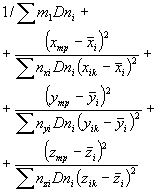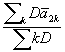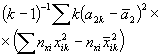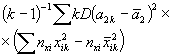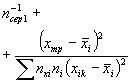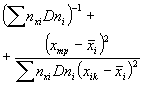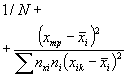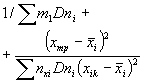
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"ГОСТ Р 51372-99 Методы ускоренных испытаний на долговечность и сохраняемость при воздействии агрессивных и других специальных сред для технических изделий, материалов и систем материалов. Общие положения.ГОСТ Р 51372-99
МЕТОДЫ
УСКОРЕННЫХ ИСПЫТАНИЙ Общие положения ГОССТАНДАРТ РОССИИ Москва СОДЕРЖАНИЕ ГОСТ Р 51372-99
Дата введения 2000-07-01 Предисловие1. РАЗРАБОТАН И ВНЕСЕН Техническим комитетом по стандартизации ТК 341 «Внешние воздействия» Госстандарта России 2. ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 29 ноября 1999 г. № 442-ст 3. Настоящий стандарт соответствует международным стандартам МЭК 60068-2-42-82 «Основные методы испытаний на воздействие внешних факторов. Часть 2. Испытания. Глава 42. Испытание Кс. Испытание контактов и соединений на воздействие двуокиси серы», МЭК 60068-2-43-79 «Основные методы испытаний на воздействие внешних факторов. Часть 2. Испытания. Глава 43. Испытание Kd. Испытание контактов и соединений на воздействие сероводорода», МЭК 60068-2-46-82 «Основные методы испытаний на воздействие внешних факторов. Часть 2. Испытания. Глава 46. Руководство по испытанию Kd. Испытание контактов и соединений на воздействие сероводорода», МЭК 60068-2-49-83 «Основные методы испытаний на воздействие внешних факторов. Часть 2. Испытания. Глава 49. Руководство по испытанию Кс. Испытание контактов и соединений на воздействие двуокиси серы», ИСО 10062-91 «Испытания на коррозионную стойкость в искусственной атмосфере при низких концентрациях загрязняющих газов» с дополнительными требованиями, отражающими потребности экономики страны 4. ВВЕДЕН ВПЕРВЫЕ ВведениеНастоящий стандарт является частью комплекса стандартов «Методы испытаний на стойкость к внешним воздействующим факторам машин, приборов и других технических изделий» (группа стандартов ГОСТ 30630), состав которого приведен в ГОСТ 30630.0.0-99, приложение Е. Настоящий стандарт соответствует международным стандартам, указанным в предисловии. При этом настоящий стандарт дополняет и уточняет методы проведения испытаний, их классификацию и состав, увязывая методы (режимы) испытаний с условиями и сроками эксплуатации изделий и охватывая всю совокупность технических изделий, что в настоящее время не имеется в международных стандартах, относящихся к внешним воздействующим факторам. В связи с указанным в настоящее время невозможно полное использование публикаций международных стандартов по внешним воздействиям в качестве государственных стандартов. В разработке стандарта принимал участие М.Л. Оржаховский (руководитель), академик Академии проблем качества Российской Федерации. Общие положения1. Область примененияНастоящий стандарт распространяется на машины, приборы и другие технические изделия (далее - изделия); полимерные материалы, металлы и сплавы (далее - материалы); детали и узлы из них, полимерные системы электрической изоляции (далее - системы материалов); защитные покрытия от коррозии (далее - покрытия), применяемые в этих изделиях. Стандарт устанавливает общие положения к методам исследовательских ускоренных испытаний на долговечность и сохраняемость в условиях воздействия агрессивных сред. Требования разделов 4 - 9 и приложений А - И настоящего стандарта в части методов определения или подтверждения (контрольные испытания) показателей долговечности и сохраняемости являются обязательными, как относящиеся к требованиям безопасности. 2. Нормативные ссылкиВ настоящем стандарте использованы ссылки на следующие стандарты: ГОСТ 9.083-78 Единая система защиты от коррозии и старения. Покрытия лакокрасочные. Методы ускоренных испытаний на долговечность в жидких агрессивных средах ГОСТ 6433.2-71 Материалы электроизоляционные твердые. Методы определения электрического сопротивления при постоянном напряжении ГОСТ 6433.3-71 Материалы электроизоляционные твердые. Методы определения электрической прочности при переменном (частоты 50 Гц) и постоянном напряжении ГОСТ 6433.4-71 Материалы электроизоляционные твердые. Методы определения тангенса угла диэлектрических потерь и диэлектрической проницаемости при частоте 50 Гц ГОСТ 10518-88 Системы электрической изоляции. Общие требования к методам ускоренных испытаний на нагревостойкость ГОСТ 15150-69 Машины, приборы и другие технические изделия. Исполнения для различных климатических районов. Категории, условия эксплуатации, хранения и транспортирования в части воздействия климатических факторов внешней среды ГОСТ 16350-80 Климат СССР. Районирование и статистические параметры климатических факторов для технических целей ГОСТ 22372-77 Материалы диэлектрические. Методы определения диэлектрической проницаемости и тангенса угла диэлектрических потерь в диапазоне частот от 100 до 5·106 Гц ГОСТ 24104-88 Весы лабораторные общего назначения и образцовые. Общие технические условия ГОСТ 25336-82 Посуда и оборудование лабораторные стеклянные. Типы, основные параметры и размеры ГОСТ 25870-83 Макроклиматические районы земного шара с холодным и умеренным климатом. Районирование и статистические параметры климатических факторов для технических целей ГОСТ 26883-86 Внешние воздействующие факторы. Термины и определения ГОСТ 30630.0.0-99 Методы испытаний на стойкость к внешним воздействующим факторам машин, приборов и других технических изделий. Общие требования ГОСТ Р 51369-99 Методы испытаний на стойкость к климатическим внешним воздействующим факторам машин, приборов других технических изделий. Испытание на воздействие влажности* * См. введение. 3. ОпределенияВ настоящем стандарте применяют следующие термины с соответствующими определениями: 3.1. полимерная система: Полимерный материал или совокупность полимерных материалов, рассматриваемых в сочетании с присоединенными неполимерными деталями применительно к конкретному типу серии или части изделия1). 1) Аналогично определяют срок службы материалов или систем изоляции в изделии. 3.2. система электрической изоляции: Изоляционный материал или совокупность изоляционных материалов, рассматриваемых вместе с относящимися к ним токоведущими частями, применительно к отдельному типу, типоразмеру или части электротехнического изделия (ГОСТ 10518, приложение 1) 3.3. ресурс материалов или систем материалов: Суммарное время, в течение которого материал или система материалов могут выполнять свои функции в работающем изделии. 3.4. срок сохраняемости в эксплуатации материалов, систем материалов: Суммарное время, в течение которого материалы или системы материалов могут выполнять свои функции при воздействии факторов внешней среды на находящееся в нерабочем состоянии изделие; последнее при этом может периодически включаться для работы. 3.5. срок сохраняемости образцов материалов или систем материалов: Условное понятие, выражающееся временем, в течение которого критерии отказа материалов или систем материалов превышают установленное критическое значение в условиях испытаний2). 2) Аналогично определяют срок службы или ресурс образцов материалов или системы изоляции. 3.6. агрессивная среда: Среда, обладающая кислотным, основным или окислительным действием и вызывающая разрушение (или ухудшение параметров) материалов и (или) изделий. 3.7. греющееся изделие: Изделие, у которого превышение температуры самой теплой точки его отдельных узлов, чувствительных к температуре, влажности, агрессивной среде, или изделия в целом над температурой внешней среды (при нагрузке, соответствующей верхнему значению температуры внешней среды) составляет 10°С и более, или у которого превышение температуры поверхности, измеренной в условиях свободного обмена воздуха после достижения теплового равновесия, над температурой внешней среды при той же нагрузке составляет 5°С и более3) (ГОСТ 15150). 3) В некоторой нормативной документации - тепловыделяющее изделие или тепловыделяющий образец. 3.8. критерий отказа: Параметр, определяющий работоспособность изделия, систем материалов, покрытия, материала4). 4) В некоторой нормативной документации - характеристика или характеристический показатель. 3.9. критическое значение критерия отказа: Предельное значение критерия отказа, при котором изделие, система материалов, покрытия, материал еще удовлетворяют предъявленным к нему требованиям в условиях эксплуатации, хранения до ввода в эксплуатацию или испытания5). 5) В некоторой нормативной документации - критерий конечной точки. 3.10. отказ системы материалов: Первый отказ любого элемента системы материалов. 3.11. срок L: Срок сохраняемости до ввода в эксплуатацию или же часть срока службы, или весь срок службы, в течение которых агрессивная среда воздействует на систему материалов, изделие, покрытие, материал, температура поверхности которых равна температуре внешней среды или превышает ее более чем на 5°С. В частности, для периода эксплуатации срок L определяется: - для греющихся изделий (в т.ч. деталей, нагрев которых является следствием выделения тепла готовым изделием или конструкцией при работе по назначению) - сроком сохраняемости в эксплуатации; - для негреющихся деталей - сроком службы; - для покрытий, основное назначение которых состоит в защите от воздействия агрессивной среды, - ресурсом. 3.12. эффективное значение: По ГОСТ 26883 и ГОСТ 15150. 3.13. коэффициент ускорения испытаний: Величина, показывающая, во сколько раз уменьшается значение показателей долговечности или срок сохраняемости при испытаниях относительно заданных значений показателей долговечности или срока сохраняемости в эксплуатации или при хранении до ввода в эксплуатацию. Примечание - На практике при испытаниях для подтверждения заданных (в частности, гарантийных) сроков под коэффициентом ускорения понимают величину, равную указанной выше и показывающую, во сколько раз уменьшается время испытаний по сравнению с заданным сроком или сроком эксплуатации или сохраняемости. 4. Сущность метода4.1. Ускорение испытания достигают ужесточением (форсированием) воздействия испытательных факторов, за исключением механических. 4.2. Ускоренные испытания на долговечность и сохраняемость проводят путем экспериментального определения зависимости срока L от значений основных воздействующих факторов внешней среды: температуры, относительной влажности воздуха, концентрации агрессивной среды. По результатам определения этой зависимости с требуемой доверительной вероятностью могут быть установлены: - срок L средний или гамма-процентный (ресурс или срок службы, или срок сохраняемости) при заданных значениях (постоянных или переменных) основных воздействующих факторов; - значения основных воздействующих факторов, при которых допустима эксплуатация изделий при заданном сроке L; - графики зависимости срока L от основных воздействующих факторов, могущие служить аттестованными нормативно-справочными данными о свойствах материала, покрытия, системы материалов, изделия; - режим ускоренных контрольных испытаний при одном значении основных воздействующих факторов; - прогнозирование зависимости изменения значений параметра-критерия отказа от продолжительности действия заданных значений основных воздействующих факторов (с учетом установленных в настоящем стандарте ограничений). Для жидких сред требования, установленные в настоящем стандарте для относительной влажности, не учитывают. 4.3 Зависимость срока L от основных воздействующих факторов определяют по формулам:
или
где А, А', В, В', m, п - постоянные коэффициенты, определяемые экспериментально по методам настоящего стандарта; Т - температура, К; η - относительная влажность, %; С - концентрация агрессивной среды, г/м3 или %. Необходимо учитывать, что для каждого материала, покрытия или системы материалов может быть получено более одной зависимости срока L от основных воздействующих факторов, при этом каждая зависимость определяется выбранными критериями, их уровнями, а также видами и уровнями других испытательных воздействий. Если математическая функция зависимости параметра-критерия отказа от времени воздействия агрессивной среды может быть представлена в виде прямой линии, вместо срока L может быть применена скорость (b2) изменения указанной функции с учетом того, что b2 = K1/ L, где К1 - постоянная величина. 4.4. Испытания проводят следующими методами: I - испытания до наступления отказа всех образцов с последующей экстраполяцией полученной зависимости срока L от величины внешних воздействующих факторов в область эксплуатационного значения фактора; II - испытания путем определения зависимости величины параметра-критерия отказа от продолжительности воздействия испытательных факторов с последующей экстраполяцией по начальной части зависимости до критического параметра-критерия отказа; III - испытания до наступления отказа части образцов. 5. Общие положения5.1. Методы ускоренных испытаний применяют для определения долговечности и сохраняемости в средах, содержащих: - один агрессивный компонент (помимо кислорода воздуха); - несколько агрессивных компонентов, если заранее известно, что только один агрессивный компонент (помимо кислорода воздуха) вызывает отказы изделия. В этом случае действием остальных компонентов пренебрегают и испытания проводят в среде компонента, вызывающего отказы. В других случаях многокомпонентных агрессивных сред эти методы могут быть применены, если все компоненты, кроме одного, содержатся в испытательной среде при рабочей концентрации. 5.2. Методы, изложенные в настоящем стандарте применяют для изделий, эксплуатирующихся в агрессивных средах. Эти методы могут быть применимы также для изделий, эксплуатирующихся в других средах, например: - в газовых заполнениях (гелий, аргон, азот и др.); в этом случае испытания проводят при давлении и влажности среды, при которых требуется определить долговечность и сохраняемость; - во влажном воздухе в случаях, когда действие влажности не сопровождается химическим взаимодействием с материалами. Примечание - При эксплуатации (или испытании) узлов и деталей, работающих в агрессивной среде под воздействием постоянного электрического напряжения (за исключением герметизированных узлов или деталей) или под напряжением 3000 В и более, могут наблюдаться дополнительные факторы, не учтенные в методах испытания настоящего стандарта. Методы, изложенные в настоящем стандарте, не предназначены для проверки электроизоляционных панелей (или материалов для них) электротехнических изделий на возможность образования токопроводящих мостиков при длительной эксплуатации изделий в газовых средах. Долговечность в этих случаях обеспечивается правильным выбором материалов панелей. 5.3. Настоящий стандарт содержит требования, общие для различных видов материалов, систем материалов, покрытий и изделий. Для испытания конкретных групп и видов материалов, систем материалов, покрытий и изделий должны быть разработаны соответствующие методы, конкретизирующие требования настоящего стандарта применительно к конкретным объектам испытаний или другой нормативной документации (далее - НД на методы испытаний). 5.4. В НД на методы ускоренных испытаний должны быть установлены результаты выполнения следующих этапов работ: - для материалов, покрытий, систем материалов - выбор формы образца: - для готовых изделий - выбор узлов, наиболее подверженных воздействию данной среды; - определение критериев отказа, характеризующих стойкость к воздействию агрессивной среды; - выбор критических значений критериев отказа; - выбор видов, последовательности и способов приложения испытательных факторов; - выбор плана и режимов испытаний, периодичности контроля показателей критериев отказа в процессе испытания, последовательности и контроля параметров после испытаний. 5.5. В НД на методы ускоренных испытаний конкретных материалов или покрытий способы приложения и виды воздействующих факторов, критерии отказа и формы образца должны соответствовать преимущественному применению материалов или покрытий в конструкции. Если возможно несколько основных применений материала или покрытия, то могут быть разработаны несколько методов испытаний. При испытании материалов в виде образцов по методам испытаний материалов результаты испытаний используют для предварительной оценки долговечности материалов. Для определения долговечности и сохраняемости материалов в составе изделия должны быть проведены испытания материалов в составе покрытий или систем материалов по методам испытаний покрытий или систем материалов, если иное не указано в НД на испытания материалов. 5.6. Испытания проводят при нескольких значениях температуры и относительной влажности среды, увеличенных по сравнению со значениями (для воздушной среды - по сравнению с рабочими или эффективными значениями сочетаний влажности и температуры воздуха, установленных в соответствующей НД), а также при нескольких концентрациях агрессивной среды, ужесточенных (как правило увеличенных) по сравнению с верхним рабочим или эффективным значением, установленным в НД на материалы, покрытия или изделия. Допускается при испытаниях не изменять значения одного или двух внешних воздействующих факторов по сравнению с рабочим или эффективным значениями в зависимости от особенностей механизма наступления отказа конкретных материалов, покрытий, систем материалов или изделий. 6. Методы отбора образцов6.1. В НД на методы испытаний конкретных материалов, покрытий или систем материалов должны быть даны соответствующие указания по конструкции образцов для испытаний и способам их подготовки. Размеры образцов выбирают с учетом размеров реальных конструкций, где предполагают применять материал или сочетание материалов. При этом размеры испытуемых образцов конструкций должны, по возможности, приближаться к реальной конструкции (выбранной в качестве типовой для данного вида изделий) с учетом экономических соображений и удобства проведения испытаний. 6.2. При испытании материалов проверяют как отдельные материалы, так и простые комбинации материалов (например, пропитанные эмалированные провода, пленкокартон). При испытаниях покрытий учитывают влияние подложки. 6.3. Для испытаний систем материалов следует применять макеты или узлы изделий. Конструкция макетов должна воспроизводить основные элементы конструкции готовых изделий или их реальных узлов. Конструкция макетов и узлов должна позволять имитировать основные эксплуатационные воздействия, способствующие старению или его выявлению. Допускается проводить испытания готовых изделий с оценкой отдельных узлов или изделия в целом. При испытании герметизированных изделий, которые в эксплуатации не подлежат разгерметизации в агрессивных средах, испытывают только наружные детали, включая оболочку, обеспечивающую герметизацию. 6.4. В НД на методы испытаний должны быть предусмотрены контрольные испытания, которым до начала испытаний на долговечность и сохраняемость подвергают образцы для проверки их качества и идентичности. 6.5. Испытания проводят на образцах, не подвергавшихся старению или износу в эксплуатации или при испытаниях, имитирующих эксплуатацию. Испытания электроизоляционных материалов и систем, а также других материалов, покрытий, систем материалов для греющихся изделий, ресурс которых при нагрузке, вызывающей нагрев материала, покрытия, системы материалов, составляет 10 - 40 тыс. ч, проводят также на образцах, подвергнутых старению на 50 и 80 % ресурса. Это требование не распространяется на неорганические материалы и системы этих материалов, не содержащие органических или элементоорганических компонентов. Рекомендуется проводить такие испытания на образцах неэлектроизоляционных полимерных материалов и систем материалов. Ускоренное тепловое старение проводят циклическим методом, подвергая образцы попеременному воздействию температуры и влажности и, если требуется, воздействию механических факторов. Режимы воздействия температуры выбирают по ГОСТ 10518, при этом лакокрасочные покрытия условно относят к тому температурному индексу электроизоляционного материала, которому соответствует температура эксплуатации лакокрасочного покрытия, указанная в его обозначении. Методы воздействия влажности - по ГОСТ Р 51369, но при этом режим увлажнения выбирают по таблице 1 настоящего стандарта в зависимости от условий эксплуатации материала, покрытия, системы материалов. Выбор режимов увлажнения
6.6. В НД на методы испытания должно быть указано минимально допустимое число образцов, требуемое для получения необходимой статистической достоверности результатов. При выборе числа образцов учитывают требования раздела 5. 6.7 Для испытаний должны применяться материалы или покрытия из одной партии, однородные по верхнему виду и удовлетворяющие соответствующим требованиям. Для проверки тождественности результатов рекомендуется проводить повторные испытания образцов, в которых применены материалы из других партий. 6.8. Маркировка образцов должна быть четкой, содержать четкое различие в процессе испытаний и оценки, не повреждаться в процессе испытаний и не искажать результатов испытаний. 7. Испытательное оборудование, материалы, реактивы7.1. Испытательная камера должна позволять поддерживать в месте расположения образцов температуру с погрешностью ±2°С; допускаются отдельные кратковременные - не более 15 мин за 6 ч - отклонения ±5°С. Перепад температуры внутри камеры в месте расположения образцов не должен превышать 2°С. 7.2. Камера для испытаний в газовых агрессивных средах дополнительно должна удовлетворять следующим требованиям: - позволять поддерживать концентрацию агрессивного газа с погрешностью ±25 % величины концентрации при испытаниях и относительную влажность с погрешностью ±5 %; - иметь устройства для перемешивания среды со скоростью 1 - 2 м/с, устройства для отбора проб среды, ввода среды, извне, эвакуации среды по окончании испытаний; - обеспечивать равномерность поступления газа в камеру и не допускать попадания струи газа на образцы. 7.3. Камера при необходимости должна иметь устройства для электрических вводов для проведения измерений и (или) для обеспечения работ изделий, а также устройство для измерения температуры воздуха или газовой среды. 7.4. Камера влажности должна обеспечить испытательный режим с отклонениями, не превышающими указанные в ГОСТ 30630.0.0. 7.5. Химические реактивы должны быть квалификации ч. или - для создания специальной среды - х. ч. или ч. д. а. - для контроля специальной среды. 7.6. Стойки и штативы для размещения образцов должны быть изготовлены из материалов, стойких к воздействию соответствующих видов газообразных агрессивных сред. 7.7. Испытательное оборудование и приборы должны быть аттестованы и проверены в соответствии с установленным порядком. 8. Проведение испытаний8.1. Перед началом испытаний проводят подготовку устройств и приспособлений. Если испытания должны проводится в газообразных средах, рекомендуемый порядок обработки указан в 8.1.1 - 8.1.5. 8.1.1. Камеру выводят на испытательный режим без размещения в ней образцов. 8.1.2. Замеры параметров испытательного режима на соответствие заданным значениям проводят периодически. Периодичность замеров устанавливают в зависимости от изменения концентрации, температуры и относительной влажности агрессивной среды. 8.1.3. В процессе обработки режима проводят необходимые корректировки заданных значений концентрации, температуры и относительной влажности агрессивной среды. 8.1.4. Установленный испытательный режим поддерживают не менее 24 ч, периодически контролируя его параметры. Затем камеру отключают. 8.1.5. Предварительную отработку режима допускается не проводить перед испытаниями новой партии образцов, если испытание предыдущей партии проводилось в том же режиме, а перерыв между испытаниями не превышал длительности этого режима. 8.2. Образцы размещают в камере и выводят ее на испытательный режим. Время начала испытательного цикла считают с момента достижения в камере требуемых параметров воздействующих факторов. Образцы рекомендуется загружать в предварительно прогретую камеру. При проведении испытаний в газовой среде образцы в камере размещают таким образом, чтобы агрессивный газ мог свободно обдувать их; после загрузки образцов повышают относительную влажность до заданного значения и в камеру подают агрессивный газ. В одной испытательной партии не должно быть образцов, выделяющих агрессивные продукты деструкции, способные вызвать повреждение соседних образцов. 8.3. Испытания проводят циклически, с повторяющимися циклами. Каждый цикл состоит из: - совместного воздействия основных факторов; - одновременного или попеременного воздействия дополнительных испытательных факторов, имитирующих другие (по сравнению с 1.2) эксплуатационные факторы. Следует учитывать, что одинаковые факторы могут либо вызывать разрушение, либо только выявлять уже произведенное разрушение (диагностические факторы) в зависимости от значения и продолжительности действия фактора, его сочетания с другими факторами и последовательности приложения испытательных воздействий. Допускается проводить нециклические испытания, если заранее известно, что разрушение вызывают только одновременно воздействующие испытательные факторы, а остальные факторы только его выявляют. При испытании в газообразных средах допускаются перерывы не более 24 ч на каждый период испытаний продолжительностью не менее 10 сут. Образцы должны находится в закрытой камере, освобожденной от испытательной среды. Время перерыва не включают в продолжительность испытаний. При продолжительности испытаний менее 10 сут перерывы не допускаются. 8.4. В НД на методы испытаний должны быть указаны виды и последовательность приложения испытательных факторов. Например, для полимерных систем (в т.ч. систем электрической изоляции), предназначенных для эксплуатации с воздействием динамических механических воздействий в воздушной среде, содержащей агрессивные газы, предпочтительно следующая последовательность: приложение основных факторов по 4.2, механические воздействия, увлажнение как диагностический фактор, контроль параметров-критериев отказа (для электроизоляционных систем - приложение испытательного напряжения). 8.5. По каждому из основных видов воздействующих факторов следует получить не менее трех экспериментальных режимов, причем один режим может быть общим для нескольких видов воздействующих факторов. Для этого проводят три или более серий испытаний. В каждой серии один из воздействующих факторов при каждом испытании изменяют, остальные сохраняют неизменными, что позволяет определить зависимости: lg L = f(lg С) при η = const; Т - const; lg L = φ(lg η) при С = const; T = const; lg L = ψ(Т) при η = const; С = const, или в соответствии с 1.3 зависимости lg b2 = f1(lg С); lg b2 = φ(lg η); lg b2 = ψ(T). 8.6. Общее число испытательных режимов, необходимых для определения влияния основных воздействующих факторов, должно быть не менее семи. Если испытания в соответствии с 5.6 проводят при одном значении одного или двух факторов внешней среды, то проводят соответственно две или одну серию испытаний. При этом общее число испытательных режимов должно быть не менее пяти или трех соответственно. Возможно несколько вариантов планов проведения эксперимента, указанных в приложении А. 8.7. При выборе граничных (как правило максимальных) испытательных значений ограничиваются значениями, при которых один доминирующий процесс разрушения заменяется другим. Эти граничные значения допускается определять при помощи косвенных критериев. При этом следует учитывать, что изменение процесса разрушения, определенное по косвенному критерию, не всегда воспроизводится при определении по прямому критерию. Если граничное значение фактора неизвестно, допускается проводить испытания по 8.8 и 9.3. Если материалы, покрытия или системы материалов предназначены для эксплуатации в воздушной среде при нормальных рабочих значениях температуры и влажности, то для проведения испытаний предпочтительно выбирать температуры из ряда 40, 50, 60, 70, 80, 90, 100°С, относительной влажности из ряда 65, 80, 95, 100 % и не менее трех значений концентрации агрессивного газа. Крайние значения диапазона испытательных концентраций выбирают в зависимости от нормированного верхнего рабочего значения концентрации с учетом возможности экстраполяции (см. 6.1). Например, при верхнем рабочем значении С = 0,005 г/м3 испытательные концентрации принимают в диапазоне 0,1 - 100 г/м3. См. также приложение Л. 8.8. Если зависимость среднего логарифмического срока L (или логарифма средней скорости b2) от какого-либо из воздействующих факторов, определенная по 8.5 и вычисленная по формуле (2), резко отлична от линейной, для окончательного установления характера этой зависимости от данного фактора проводят дополнительные испытания. Эти испытания проводят не менее чем при двух значениях испытательного фактора, не совпадающих с прежними значениями (предпочтительно, чтобы дополнительные значения лежали между первоначальными). При этом предпочтительно проводить параллельные испытания материалов, покрытий или систем материалов, характер зависимости которых от данного испытательного фактора не вызывает сомнений. Допускается не проводить дополнительных испытаний, если: - при первоначальных испытаниях были соблюдены требования настоящего пункта в части общего числа значений испытательных факторов; - отклонения от линейной зависимости имеются (или предполагаются) только для зависимостей от концентрации и влажности, а результаты обработаны по вариантам 4 и 5 приложения А. 8.9. При включении в испытательный цикл механических воздействий в НД на методы испытаний должны быть указаны их интенсивность, направление и время действия. Если в цикл вводят увлажнение как фактор, выявляющий разрушение образцов, то образцы изделий и систем материалов подвергают увлажнению в соответствии с таблицей 1. Рекомендуется вместо введения механических воздействий в циклы испытаний обеспечивать воздействие механических нагрузок на образцы в процессе воздействия агрессивных сред. 8.10. Если предполагаемый срок L можно установить на основе предварительной информации, то продолжительность воздействия основных испытательных факторов выбирают в каждом цикле так, чтобы среднее число циклов до наступления отказа составляет 7 - 10. Если предполагаемый срок L установить нельзя, продолжительность воздействия факторов в каждом цикле выбирают исходя из необходимости получения достаточной информации в результате измерения параметров образцов после каждого цикла. При этом продолжительность циклов предпочтительно устанавливать различной: меньшую на первых циклах и большую - на последующих. Среднее число циклов для каждого образца вычисляют как среднее арифметическое до наступления отказов, включая цикл, в котором произошел отказ. Поскольку число циклов может влиять на долговечность и сохраняемость образцов в условиях испытаний, при которых средние числа циклов при каждом режиме испытаний не отличаются друг от друга более чем в два раза. При этом среднее число циклов при любом испытательном режиме должно быть не менее семи. Если при испытаниях на одном испытательном режиме наблюдался отказ у 100 % образцов, а при других испытательных режимах за такое же время наблюдался отказ у менее 50 % образцов, время выдержки увеличивают в два-три раза без изменения параметров испытательного режима. Если среднее число циклов будет меньше семи, испытания повторяют (если требуются более достоверные результаты для данного материала, покрытия, системы материалов), но при этом уменьшают продолжительность циклов без изменения параметров испытательного режима. 8.11. При испытании изделий или систем материалов отказом считают первый отказ любого элемента или системы. Допускается продолжать испытания образца для оценки поведения остальных элементов. При этом принимают во внимание возможность частичного повреждения остальных элементов изделия или системы при отказе первого. Время до отказа остальных элементов учитывают отдельно и не включают в срок L. В случаях, когда необходимо получить данные по одному элементу изделия или системы материалов, допускается усиление (защита) других элементов, не влияющих на стойкость изучаемого элемента. 8.12. Для электроизоляционных материалов и систем изоляции электротехнических изделий за критерий отказа рекомендуется применять пробой при воздействии испытательного напряжения. Значение испытательного напряжения выбирают в зависимости от функции, которую выполняют материалы в изделии или системе материалов. Значение испытательного напряжения должно быть достаточно высоким, чтобы можно было установить критическую степень деструкции изоляции, но в то же время не настолько высоким, чтобы изменить характер старения изоляции, определяемый воздействием основных факторов, или вывести изоляцию из строя в том состоянии, когда она еще способна выполнять свои функции в данном изделии или системе материалов. В НД на методы испытаний указывают длительность приложения испытательного напряжения и стадию цикла, на которой его прикладывают. Для электроизоляционных материалов и систем изоляции неэлектротехнических изделий за критерий отказа принимают пробой при воздействии испытательного напряжения или изменения других параметров (например, удельного объема сопротивления, волновых параметров, тангенса угла диэлектрических потерь или же механической прочности) до установленного критического значения, если этими параметрами в большей степени, чем приложенным напряжением, определяется работоспособность материала или системы изоляции. Для неэлектроизоляционных материалов и конструкций критерии отказа указывают в НД на методы испытаний. 8.13. При выборе критерия отказа учитывают фиксированное значение измеряемого параметра, а не степень его изменения по отношению к исходному значению. При исследовании систем изоляции (конструкций), для которых в различных видах изделий критичными могут быть разные уровни измеряемого параметра, рекомендуется в качестве критерия отказа принимать несколько уровней параметра и соответственно определять разные ресурсы. Допускается при сравнении материалов использовать при выборе критерия степень изменения измеряемого параметра по отношению к исходному значению. При этом следует учитывать, что этот способ может привести к необоснованной отбраковке образцов с более высокими начальными значениями параметра, но с несколько большей скоростью его изменения. За исходные значения параметра при этом способе принимают (если иное не установлено в НД на испытания конкретных материалов) среднее арифметическое результатов испытаний при количестве образцов, определенных по статистическим методам, обеспечивающим попадание среднего (с заданной относительной ошибкой) в интервал с заданной доверительной вероятностью. При этом выбранная доверительная вероятность должна соответствовать доверительной вероятности, выбранной для подсчетов срока L. Необходимость и методику предварительной стабилизации свойств образцов (например, тренировка, выдерживание в кондиционированных условиях) устанавливают в стандартах на методы испытаний. 8.14. В НД на методы испытаний должна быть установлена стадия цикла, на которой проводят измерения показателей-критериев отказа или приложение воздействий, выявляющих произведенные разрушения. В частности, если измерения или приложение выявляющих воздействий проводят после таких разрушающих воздействий, влияние которых изменяется во времени, должно быть указано время, в течение которого после разрушающего воздействия должно быть проведено измерение или приложено выявляющее воздействие. Предпочтительно, чтобы указанные измерения проводились в одинаковых условиях, а уровень выявляющих воздействий был одинаков во всех экспериментальных режимах, независимо от уровня разрушающих воздействий в данном режиме. При нециклических испытаниях через определенные интервалы времени, установленные в программе испытаний в зависимости от скорости процесса разрушения образца и предполагаемой общей продолжительности испытаний, из испытательной камеры извлекают образцы в количестве, принятом в соответствии с 6.6, для измерения параметра-критерия отказа. Если скорость процесса разрушения неизвестна, параметр-критерий отказа измеряют с интервалами времени по таблице 2. В технически возможных случаях вместо указанного порядка измерения рекомендуется проводить непрерывное измерение параметра-критерия отказа. Таблица 2 Выбор периодичности измерения параметров-критериев отказа
8.15. Испытания по методу I являются предпочтительными. 8.16. Испытания по методу II можно проводить в следующих случаях, указанных в 8.16.1 и 8.16.2. 8.16.1. Если заранее известно, что математическая функция зависимости значения параметра-критерия отказа от продолжительности воздействия испытательных факторов может быть представлена прямой линией. 8.16.2 Если невозможно проводить испытания по методу I, в этих случаях экспериментальным путем находят приближенную математическую функцию зависимости параметра-критерия отказа от продолжительности воздействия испытательных факторов и представляют ее в виде прямой линии. 8.16.3. При испытаниях применяют метод, указанный в приложении А. 8.17. Испытания по методу III являются комбинацией методов I и II. Метод допускается применять с целью сокращения общей продолжительности испытаний в случаях, когда ожидается (но окончательно не подтверждено), что зависимость математической функции параметра-критерия отказа f(П) от продолжительности может быть представлена в виде прямой линии (например, если за критерий отказа принят пробой, или при воздействии испытательного электрического напряжения). Испытания проводят следующим образом. 8.17.1. В наиболее жестких режимах (не менее чем при двух значениях испытательных факторов в каждой серии испытаний) испытания проводят по методу I. 8.17.2. В слабых режимах каждой серии испытания проводят в следующем порядке: а) для испытаний по соответствующему режиму применяют удвоенное число образцов; б) через 15 - 20 % ожидаемого срока L определяют значение f(П) у половины испытуемых образцов (или отдельно элементов конструкции) и вычисляют среднее этих значений (например, среднее логарифмов значений пробивных электрических напряжений); в) если у оставшихся образцов не наступили отказы, то спустя 40 - 60 % ожидаемого срока L определяют значения f(П) у половины оставшихся образцов и вычисляют среднее этих значений; г) по полученным данным в масштабе f(П) от продолжительности (τ) проводят экстраполяцию по продолжительности до критического значения критерия отказа и прогнозируют средний срок в этом режиме, при этом на график наносят среднее значение f(П). Здесь f(П) - функция параметра-критерия отказа (например, lg 1/и, где и - значение пробивного напряжения); τ - суммарная продолжительность воздействия испытательной среды во всех проведенных циклах испытаний; д) определяют средний срок L в данном режиме по результатам двух других режимов каждой серии испытаний путем линейной экстраполяции соответственно в масштабе: lg L - lg С или lg L - lg η или lg L - 1/Т; е) сравнивают средние сроки L, определенные по перечислениям г и д; ж) если между сроками (перечисление е) различия несущественны, определяют значение f(П) оставшихся образцов и по этим данным уточняют средний прогнозируемый срок в данном режиме. Этот срок принимают для расчетов по разделу 6 настоящего стандарта; з) если между сроками (перечисление е) различия существенны, то испытания оставшихся образцов продолжают до наступления отказа в режиме испытания. Полученные при этом сроки L принимают для расчета по разделу 9 настоящего стандарта; и) линейную экстраполяцию по перечислениям г и д проводят при помощи метода наименьших квадратов с определением дисперсии по срокам L; сравнение сроков по перечислению е проводят при помощи дисперсионного анализа с использованием критерия Фишера. 9. Обработка результатов9.1. Результаты испытаний выражают в виде математической зависимости срока L от основных воздействующих факторов по формулам (1) и (2). Допускается применять графические зависимости. По результатам ускоренных испытаний проводят экстраполяцию результатов в области эффективных значений испытательных факторов. Эффективные значения определяют по приложению В. Экстраполяцию следует проводить не более чем на 50 % разности логарифмов максимального и минимального из воздействующих значений относительной влажности и концентрации коррозионно-агрессивного агента и на 50 % разности между максимальным и минимальным значениями испытательных температур в масштабе 1/Т. Допускается расширять пределы экстраполяции, если в результате изучения механизма возникновения отказа выявлено, что в расширенных пределах не должно происходить изменения коэффициентов формул (1) и (2). 9.2 Экспериментальные данные для получения аналитической зависимости срока L материала, покрытия или систем материалов от температуры, влажности и концентрации агрессивной среды обрабатывают по методу наименьших квадратов с вычислением среднего логарифмического срока L, коэффициентов зависимостей (8.1) и, если требуется, нижних доверительных границ для среднего, а также математических ожиданий требуемых вероятностей безотказного хранения и безотказной работы (гамма-процентных сроков L) и нижних доверительных (толерантных) границ для этих показателей. Возможно также определение вероятности безотказной работы (или безотказного хранения) при заданных ресурсе (или сроке сохраняемости в эксплуатации), температуре, влажности и концентрации агрессивной среды и выбранной доверительной вероятности. Способ расчетов для метода I приведен в приложениях Б - Е. Способ расчетов для метода II приведен в приложении Б с использованием приложений В - Е. 9.3. Если зависимость среднего логарифмического срока L (или логарифма средней скорости b2) от какого-либо из воздействующих факторов, определенная по 8.5 и вычисленная по формуле (2) в соответствии с 4.3, существенно отлична от линейной (что проверено по приложению Д), то после испытания по 8.8 экспериментальные данные обрабатывают по линейной части зависимости логарифма срока от какого-либо из воздействующих факторов, причем не менее чем по трем экспериментальным точкам, исключая из рассмотрения значения факторов, более жесткие, чем значения при точке перегиба. 9.4 Если результаты испытаний используют для установления режима ускоренных контрольных испытаний при одном значении каждого испытательного фактора, определяют коэффициент ускорения испытаний следующим образом: а) в соответствии с выбранными значениями испытательных параметров определяют среднее значение коэффициента ускорения Куск по формуле:
где хэ, уэ, zэ - значения х, у, z (формула А.1 приложения А), соответствующие эффективным значениям основных воздействующих факторов; xи, yи, zи – значениях x, y, z (формула А.1 приложения А), соответствующие значениям воздействующих факторов при испытании. Значения воздействующих факторов испытательной среды предпочтительно выбирать такими, чтобы коэффициент ускорения был не более 400 с учетом требований 9.3; б) по результатам испытания определяют нижнюю доверительную границу среднего значения и нижние толерантные границы коэффициентов ускорения с необходимой вероятностью; в) в качестве коэффициента ускорения Куск для узла или детали принимают нижнюю толерантную границу, вычисленную с доверительной вероятностью 0,95 (если другие условия не указаны в документации на изделие) с требуемой вероятностью безотказной работы для изделий. Коэффициент ускорения Куск для изделия в целом принимают равным среднему значению коэффициентов ускорения испытаний, установленных для узлов и деталей определенного вида изделий; г) продолжительность ускоренных контрольных испытаний изделия τи определяют по формуле:
где τэ - продолжительность воздействия агрессивной среды на изделие, принятая для эксплуатации или хранения и установленная в документации на изделие, при этом учитывают определение срока L (раздел 3). При предъявлении к одним и тем же видам изделий требований по эксплуатации в разных средах испытания проводят на разных образцах. Если одно и то же изделие предназначено для эксплуатации последовательно в разных средах, то допускается проводить испытания последовательно на одних и тех же образцах. 9.5. Особенности испытаний лакокрасочных покрытий в газообразных агрессивных средах и методов обработки результатов этих испытаний приведены в приложении Ж. 9.6. Форма протокола испытаний приведена в приложении И. ПРИЛОЖЕНИЕ
А
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
и = а1 + а2 х + а3 у + а4 z, |
(A.1) |
где a1 = А'; аг = В'; а3 = -т; а4 = -п;
х= 1/T; y = lg C; z = lg h;
А'; В'; т; п - постоянные по формуле (2) настоящего стандарта;
и = lg L (или и = lg b2)
При этом в вариантах 1 - 3 коэффициенты а2, а3, a4 являются неизменными, так что при обработке результатов определяют их значение. Дисперсии для этих вариантов определяют по всей поверхности отклика.
В вариантах 4 и 5 коэффициент а2 (или а3 и а4) различен в разных поддиапазонах испытательного диапазона, поэтому результаты удобнее обрабатывать графоаналитическим методом, определяя коэффициент а2 и не определяя коэффициенты а3 и а4. Зная коэффициент а2 и определив коэффициенты а1k и для различных концентраций, при которых проводился эксперимент, можно построить семейство линий и = f(х) и определить средние значения и при заданных условиях эксплуатации. Дисперсии в этих вариантах удобнее определять для каждой линии u = f(x) в отдельности с использованием данных всех испытаний.
Примечание - На рисунках А.1 - А.4 для простоты изложения приведены схемы серий испытаний для получения зависимостей
L = f(T) и L = f(с) при η = const.
Аналогично в испытания включают дополнительно серию испытаний для получения зависимости L = f(η).
Варианты 1 - 5 применяют, когда в каждом режиме испытывают одинаковые образцы.
Вариант 6 относится к испытаниям в одном из наиболее жестких режимов образцов конструкций или готовых изделий и параллельным по всем требуемым режимам испытаниям образцов подобия (испытания по методам для материалов стандартных образцов из тех же видов материалов и (или) покрытий, которые применены в конструкциях или изделиях), или испытаниям малогабаритных готовых изделий или макетов.
Выбор режимов для образцов конструкций или готовых изделий проводят с учетом требований 9.3 и 9.4, для образцов подобия - по одному из вариантов 1 - 5.
Вариант 6 применяют, если это указано (с учетом требований подобия) в НД на методы испытаний готовых изделий или конструкций.
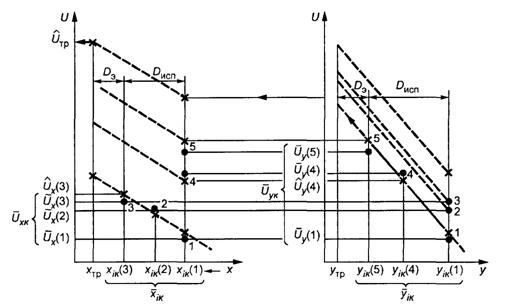
Рисунок А.1 - Схема эксперимента по варианту 1
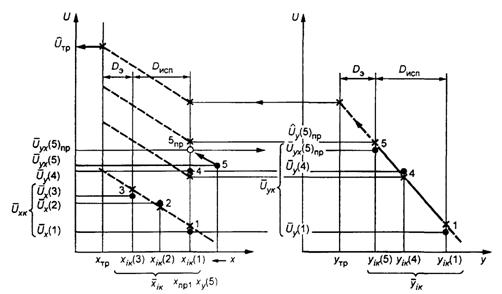
Рисунок А. 2 - Схема эксперимента по варианту 2
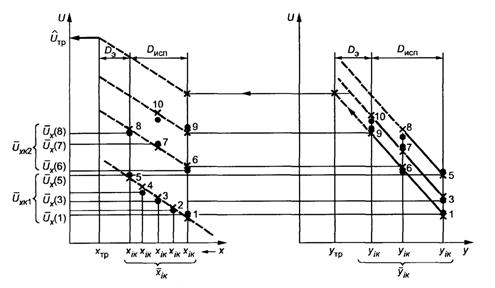
Рисунок А.3 - Схема эксперимента по варианту 3
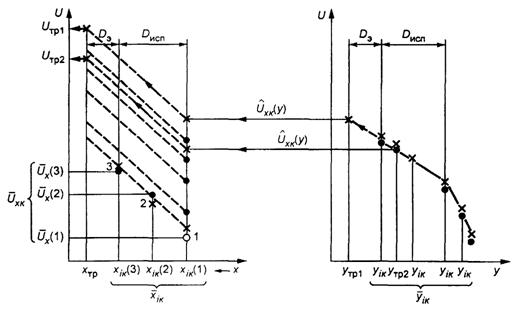
Рисунок А.4 - Схема эксперимента по варианту 4
Условные обозначения на рисунках А.1 - А.4:
Dисп - диапазон испытательных значений; Dэ - допустимый диапазон экстраполяции (Dэ = 0,5 Duсп); 1, 2, 3 … - номера испытательного режима; «—» - интерполяция в диапазоне Dисп; «-----» - экстраполяция в диапазоне Dэ; «•» - фактические испытательные точки, × - точки, полученные расчетом или экстраполяцией; ° - приведенная точка.
А.2. Общая схема обработки результатов испытаний для определения показателей надежности
А.2.1. Определяют срок L по результатам испытаний в соответствии с А.2.1.1 и А.2.1.5.
А.2.1.1. Результаты испытаний начинают обрабатывать с вычисления срока L, полученного при испытаниях каждого образца. Этот срок вычисляют в часах как суммарное время воздействия среды во всех циклах испытаний при данном режиме испытаний, за вычетом длительности воздействия в последнем цикле, после которого наступил отказ образцов (половину длительности не вычитают, если методика определения параметров образца позволяет обнаружить момент наступления отказа в процессе воздействия испытательной среды).
Для предварительной оценки при испытаниях в наиболее легких режимах допускается применять значение срока L для 50 %-ного образца (медианное значение).
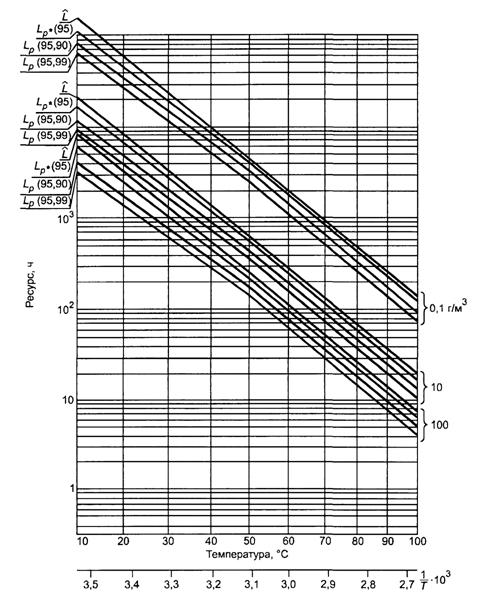
Рисунок А.5 - Зависимость ресурса от температуры для проводов ПЭТВ в воздушной среде, содержащей оксиды азота разных концентраций при относительной влажности 100 %, нижние доверительные пределы для Lр (95) и нижние толерантные пределы для различных вероятностей безотказного хранения Lp (95, 90) и Lp (95, 99)
А.2.1.2. Затем вычисляют средний срок L как среднее арифметическое всех сроков L образцов, испытывавшихся в данном режиме.
А.2.1.3. После этого вычисляют логарифмы каждого срока L и средний логарифмический срок L в каждом режиме (среднее арифметическое логарифмов сроков L).
А.2.1.4. При необходимости результаты испытаний корректируют, исключая из рассмотрения образцы с резко выделяющимися значениями логарифмов. Резко выделяющиеся значения оценивают по приложению Д.
А.2.1.5. Затем для каждого режима испытаний вычисляют среднеарифметический срок L (среднее арифметическое логарифмов сроков L всех оставшихся для рассмотрения образцов).
А.2.2. Определяют вид статистического распределения экспериментальных данных (логарифмически нормальное распределение, распределение Вейбулла или нормальное распределение) по статистическим справочникам.
Если данные могут быть описаны двумя или тремя видами распределений или вид распределения неопределенный, дальнейшую обработку проводят как для логарифмически нормального распределения.
Далее в А.2.3 - А.2.8 приводится порядок вычисления необходимых параметров для статистических распределений логарифмически нормального и Вейбулла. Порядок вычисления для нормального распределения приведен в А.2.9.
А.2.3. Следующим этапом обработки экспериментальных данных является вычисление коэффициентов формулы (1). Таким образом определяют параметры поверхности отклика (или линии регрессии).
Порядок вычисления коэффициентов принимают в зависимости от варианта эксперимента в соответствии с разделом А.1 и вычисления проводят по разделу А.3.
После подстановки
полученных данных в формулу (А.1) можно вычислить средние значения U при
испытательных или других требуемых значениях воздействующих факторов
(соответственно ![]() и
и ![]() и построить графики
зависимостей Lcp от температуры,
концентрации агрессивной среды и влажности воздуха (на рисунке А.5 в качестве
примера приведены графики зависимости от температуры и концентрации при
постоянной влажности).
и построить графики
зависимостей Lcp от температуры,
концентрации агрессивной среды и влажности воздуха (на рисунке А.5 в качестве
примера приведены графики зависимости от температуры и концентрации при
постоянной влажности).
Примечание - Если при построении графиков появляются сомнения в линейности зависимостей U(х), U(у) или U(z) во всем диапазоне испытательных факторов, проводят проверку гипотезы линейности по приложению Д.
А.2.4. Определяют общую дисперсию экспериментальных точек относительно вычисленной поверхности (или линии регрессии):
|
|
(A.2) |
где ui - логарифмы срока L каждого образца из числа оставленных для рассмотрения, подбираемые для каждого режима испытаний;
![]() - логарифмы
срока L, полученные
по формуле
(А.1) или графику, построенному для каждого режима испытаний;
- логарифмы
срока L, полученные
по формуле
(А.1) или графику, построенному для каждого режима испытаний;
fs - число степеней свободы.
ui,
![]() , fs а также s выбирают
по указаниям, приведенным для каждого конкретного варианта эксперимента по разделу А.3.
, fs а также s выбирают
по указаниям, приведенным для каждого конкретного варианта эксперимента по разделу А.3.
Примечание - Если проводилась проверка гипотезы линейности или при циклических испытаниях (в случае измерения параметров-критериев отказа в конце цикла) все отказы в каком-либо из режимов произошли только в одном или двух циклах, то дисперсию определяют по результатам вычисления дисперсии для каждого режима испытаний в данной серии в соответствии с приложением Д. Если имеются сомнения в однородности дисперсий экспериментальных точек каждого режима испытаний данной серии, проводят проверку гипотезы однородности дисперсий в соответствии с приложением Е, а при обнаружении неоднородности дисперсий - проводят вычисления по приложению Е. При неодинаковом количестве образцов в различных режимах испытаний обработку результатов проводят в соответствии с приложением Е.
А.2.5. Определяют дисперсию средних значений поверхности отклика (дисперсию, характеризующую возможное смещение генерального среднего относительно поверхности отклика, вычисленной по выборочным данным). Эту дисперсию вычисляют при заданных (требуемых) значениях воздействующих факторов по формулам:
где N - общее число образцов, применяемых при всех режимах испытаний (при наличии перегиба зависимости и от х, у или z под «всеми режимами испытаний» понимают режимы по 9.3);
хтр, утр, zтр - параметры требуемых значений воздействующих факторов;
xik, уik, zik - параметры испытательных значений воздействующих факторов (параметры испытательных режимов), отобранные для каждой серии испытаний;
![]()
![]() ,
, ![]() - по формуле (А.15);
- по формуле (А.15);
пi - число образцов, оставленных для рассмотрения в каждом испытательном режиме;
nхi, nyi, nzi - число испытательных режимов в данной серии при постоянной температуре (концентрации влажности соответственно);
i - номер режима испытаний.
В формуле (А.4) 1/N определяется смещением среднего относительно среднего выборочного. В членах:
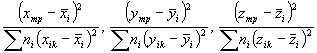
знаменатели определяются дисперсиями коэффициента регрессии и по х, у и z, а числители определяются увеличением дисперсии по мере удаления от центра испытаний.
В вариантах 4 и 5, где дисперсию вычисляют не по отношению к поверхности отклика, а по отношению к линии регрессии, последние два члена формулы (А.4) могут отсутствовать или заменяться членом, определяющим регрессию среднего значения данных и полученным при других концентрациях или влажностях. Конкретные выражения для b и значения N выбирают по указаниям, приведенным для каждого варианта А.3.
Примечание - Если определяют коэффициент ускорения (формула (3), при подсчете коэффициента b вместо формулы (А.4) применяют формулу
|
|
(A.4a) |
A.2.6. Определяют нижнюю доверительную границу среднего логарифмического значения срока L или коэффициента ускорения при заданной доверительной вероятности Р* (или уровню значимости L = 1 - Р*)
|
|
(A.5) |
где Up* - нижняя доверительная граница среднего логарифмического срока L или коэффициента ускорения по 9.4 при заданной доверительной вероятности;
t - распределение доверительных отклонений в малой выборке (распределение Стьюдента), определяемое по статистическим таблицам для заданного уровня доверительной вероятности Р* и числа степеней свободы fst для всех вариантов эксперимента, кроме варианта 4;
![]() - значение
среднего логарифмического срока L или коэффициента ускорения по 9.4
при требуемых значениях воздействующих факторов, определяемое по формуле (А.1) или графикам зависимостей: L'ср = f(toС), L'ср = f(С); L' = f(η).
- значение
среднего логарифмического срока L или коэффициента ускорения по 9.4
при требуемых значениях воздействующих факторов, определяемое по формуле (А.1) или графикам зависимостей: L'ср = f(toС), L'ср = f(С); L' = f(η).
Примечание - Вероятности Р* и Р являются различными понятиями, и их значения могут различаться, однако рекомендуется устанавливать значение Р* таким же, как значение Р.
А.2.7. Для логарифмически нормального распределения определяют нижнюю логарифмическую доверительную границу (при заданной доверительной вероятности Р*) для срока L или коэффициента ускорения по 9.4 при заданной вероятности безотказной работы Р (величине γ).
|
|
(A.6) |
где Up - нижняя логарифмическая доверительная граница срока L или Куск по 9.4 при заданной вероятности безотказной работы (величина j);
Uα - квантиль нормированного нормального распределения, определенная для требуемой вероятности безотказной работы;
Zp - квантиль удвоенной нормированной функции Лапласа, определенная для доверительной вероятности Р*.
В формуле (А.6) второй
член в скобках определяет дисперсию дисперсии для случая, когда общее число
образцов N ≥ 30. Если в порядке исключения при испытании окажется
необходимым принять меньшее число образцов, второй член формулы заменяют на ![]() , где χ2 - полученное из
статистических таблиц значение функции χ2,
взятое из вероятности (1 - Р*)/2
и числа степеней свободы fs1 = N - 1. С учетом формул (А.3) и (А.5) формула (А.6) может быть заменена на
следующую:
, где χ2 - полученное из
статистических таблиц значение функции χ2,
взятое из вероятности (1 - Р*)/2
и числа степеней свободы fs1 = N - 1. С учетом формул (А.3) и (А.5) формула (А.6) может быть заменена на
следующую:
|
|
(A.7) |
A.2.7.1. Затем определяют Uγ - математическое ожидание логарифма гамма-процентного срока L, соответствующее требуемой вероятности безотказной работы или хранения; L -математическое ожидание гамма-процентного срока L; Lp - Lp*γ - нижнюю границу гамма-процентного срока L при заданных доверительной вероятности Р* и вероятности безотказной работы или хранения Р (нижнюю толерантную границу срока L)
А.2.7.1.1. Для логарифмически нормального распределения:
|
|
(A.5a) |
|
|
(A.6a) |
|
|
(A.7a) |
А.2.7.2.2. Для распределения Вейбулла
|
|
(A.5б) |
где bВ - параметр формы распределения Вейбулла для коэффициента вариации UB, определяемого по формуле
|
|
(A.6б) |
|
|
(A.7б) |
А.2.8. Пользуясь формулами (А.6), (А.7) или (А.5а) - (А.7а) и задавшись вероятностью Р* (обычно 0,9 или 0,95), строят графики зависимостей Up = f(χ) (или LP = f(t°C) в соответствующем масштабе) для нескольких концентраций и влажностей агрессивной среды и нескольких наиболее употребительных требуемых вероятностей безотказного хранения и (или) работы (рисунок А.5).
Пользуясь этими графиками, можно решить обратную задачу - определить вероятность безотказной работы (хранения) при заданных ресурсе (сроке сохраняемости) и условиях эксплуатации (температуре концентрации и влажности агрессивной среды).
Вероятность безотказного хранения или работы можно определить и расчетным путем, вычислив Uα по формуле, полученной из формулы (А.7), подставив вместо Up логарифмы заданного срока L(Uзад):
|
|
(A.8) |
По найденному Uα при помощи таблиц удвоенной нормированной функции Лапласа определяют значение вероятности безотказного хранения или работы.
А.2.9. Для нормального распределения представленные выше расчеты видоизменяют, как указано ниже.
А.2.9.1. Определяют срок L в соответствии с А.2.1.
А.2.9.2. После этого вычисляют средний срок (среднее арифметическое сроков L) L
|
|
(A.5в) |
где Li - сроки, полученные для каждого образца в данном режиме;
пic - число испытуемых образцов.
А.2.9.3. Результаты
испытаний при необходимости корректируют в соответствии с А.2.1.3, но при этом вычисляют средний
арифметический корректированный срок каждого режима ![]() вместо среднего
логарифмического срока
вместо среднего
логарифмического срока ![]() .
.
А.2.9.4. Определяют
дисперсию ![]() срока L в
соответствии с А.2.1.4, заменяя при вычислениях U на L с теми же индексами.
срока L в
соответствии с А.2.1.4, заменяя при вычислениях U на L с теми же индексами.
А.2.9.5. Далее применяют требования А.2.4 - А.2.7, А.2.7.1, заменяя при вычислениях значения показателей логарифмов сроков службы U на показатели сроков службы L с теми же индексами.
В этом случае при вычислениях по А.2.6. получают нижнюю доверительную границу гамма-процентного срока L при заданной доверительной вероятности Р*.
А.3 Определение коэффициентов формул поверхности отклика и дисперсий для разных вариантов эксперимента
А.3.1. Вариант 1 (рисунок А.1)
Дано
1-я серия: L = f(t°С) при С = const, η = const;
2-я серия: L = f(С) при t°C = const, η = const;
3-я серия: L = f(η) при t°С = const.
Коэффициент а2 в формуле (А.1) определяют следующим образом.
Сначала определяют
средние значения ![]() и
и ![]() в 1-й серии испытаний
(при различных температурах и неизменных концентрации и влажности):
в 1-й серии испытаний
(при различных температурах и неизменных концентрации и влажности):
где пxi - число испытательных режимов в данной серии (для рассматриваемой серии - число значений температур);
хik - значение х для каждой температуры испытаний в данной серии;
![]() -
корректированный средний логарифмический срок L (или
логарифм средней скорости b2) при каждой температуре испытаний в
данной серии. Коэффициент а2 находят по формуле:
-
корректированный средний логарифмический срок L (или
логарифм средней скорости b2) при каждой температуре испытаний в
данной серии. Коэффициент а2 находят по формуле:
|
|
(A.10) |
Аналогично находят коэффициенты а3 и a4.
Определяют ![]() и
и ![]() (или соответственно
(или соответственно ![]() и
и ![]() ):
):
где nyi и nzi - число значений испытательных режимов соответственно 2 и 3-й серий (для рассматриваемых серий - число значений концентраций или влажности);
yik, zik - значения у и z для каждой испытательной концентрации (или соответственно влажности) в данных сериях;
![]() и
и ![]() - корректированный средний
логарифмический срок или логарифм средней скорости b2 при каждой
испытательной концентрации или влажности в данной серии. Коэффициенты а3
и а4 находят по формулам:
- корректированный средний
логарифмический срок или логарифм средней скорости b2 при каждой
испытательной концентрации или влажности в данной серии. Коэффициенты а3
и а4 находят по формулам:
Для определения
коэффициента а, вначале находят средние ![]() :
:
|
|
(A.15) |
где m1 - общее число испытательных режимов;
![]() - корректированный средний
логарифмический срок L или логарифм средней скорости b2 в каждом режиме
испытаний;
- корректированный средний
логарифмический срок L или логарифм средней скорости b2 в каждом режиме
испытаний;
хi, уi, zi - значения х, у, z для каждого испытательного режима.
Коэффициент а1 находят по формуле:
|
|
(A.16) |
Далее вычисляют дисперсии. В начале находят дисперсию экспериментальных точек относительно вычисленной поверхности по формуле (2).
|
fs = N - k - 1, |
(A.17) |
где k - число серий испытаний.
Примечание - Если в соответствии с 8.5 проводилось три серии испытаний, fs = N - 4.
Формула (А.2) принимает вид:
|
|
(A.18) |
Примечание - Если проводилась проверка гипотезы линейности или если при циклических испытаниях (в случае измерения параметров-критериев отказа в конце цикла) все отказы в каком-либо из режимов произошли в одном или двух циклах, то дисперсию вычисляют по результатам вычислений дисперсий для каждого режима испытаний данной серии в соответствии с приложением Д. Если имеются сомнения в однородности дисперсии экспериментальных точек каждого режима испытаний данной серии, проводят проверку гипотезы однородности дисперсий в соответствии с приложением Е, а при обнаружении неоднородности дисперсий проводят вычисления по приложению Е. При неодинаковом количестве образцов в различных режимах испытаний обработку результатов проводят в соответствии с приложением Е.
После этого определяют дисперсию средних значений поверхности отклика, при этом формулы (А.3) и (А.4) принимают вид:
|
|
(A.19) |
![]()
|
|
(A.20) |
(См. примечание к А.2.4).
А.3.2. Вариант 2 (рисунок А.2)
Дано
1-я серия: L =f(t°С) при С = const, η = const;
2-я серия: L = f(С) при различных t°C, η = const;
3-я серия: L = f(η) при различных t°C, С = const.
Коэффициент а2 в формуле (А.1) подсчитывают так же, как в варианте 1 по формуле (А.10). При подсчете коэффициентов а3 и а4 в начале (во 2 или 3-й серии данных) значения и, полученные при различных температурах, приводят к какой-либо одной температуре. При этом выбирают значение температуры, при которой имеется максимальное число данных. Приведение проводят по формулам:
|
|
(A.21) |
|
|
(A.22) |
где хпр - значение х для температуры, к которой проводится приведение;
ху, хz - значения х для температуры, данные при которой приводятся к хпр;
![]() ,
, ![]() - средние значения и,
полученные при температурах хy или хz и
при соответствующих концентрации и влажности;
- средние значения и,
полученные при температурах хy или хz и
при соответствующих концентрации и влажности;
![]() ,
, ![]() - значения
- значения ![]() ,
, ![]() , приведенные
к температуре, соответствующей хпр.
, приведенные
к температуре, соответствующей хпр.
После получения всех
необходимых приведенных значений находят a3 и а4 так же, как в варианте 1,
подставляя в формулах (А.13) и (А.14) в соответствующих местах ![]() или
или ![]() вместо
вместо ![]() или
или ![]() .
.
Коэффициент а1 находят аналогично
варианту 1, соответственно (где требуется) подставляя в формуле (А.3) значение ![]() и
и ![]() вместо
вместо ![]() .
.
Дисперсии S2 и ![]() =
= ![]() вычисляют так же, как
в варианте 1.
вычисляют так же, как
в варианте 1.
А.3.3. Вариант 3 (рисунок А.3)
Дано
L = f(t°С), L = f(C) и L = f(η) при нескольких температурах, концентрациях и влажностях. В начале проверяют гипотезу параллельности. Для этого вычисляют параметры зависимостей U = f(t°C) при С = const и η = const, для чего данные группируют в серии, причем в каждую серию входят данные, полученные при какой-то одной концентрации и влажности и различных температурах. В этом случае формула (А.1) примет вид:
|
Uk = a1k + a2kx, |
(A.23) |
где к - номер серии испытаний при постоянных концентрации и влажности (в последующем также число серий испытаний);
Uk, a1к - значения U и al для каждой зависимости;
а2к - постоянный коэффициент для каждой зависимости.
Графики Uk = f(х), постоянные по формуле (А.23), дают семейство линий регрессии. Для проверки гипотезы параллельности требуется сравнить дисперсию, связанную с рассеянием угловых коэффициентов линии регрессии, со средней дисперсией экспериментальных точек относительно линий регрессий.
Для получения дисперсии угловых коэффициентов сначала подсчитывают угловые коэффициенты а2k для каждой серии испытаний при каждой постоянной концентрации аналогично подсчету коэффициента а2 в варианте 1 [формулы (А.9) и (А.10)]. После этого находят среднее арифметическое всех полученных угловых коэффициентов:
|
|
(A.24) |
Затем определяют дисперсию, связанную с рассеянием угловых коэффициентов:
|
|
(A.25) |
где xik, ![]() , nхi
- то же, что в формуле (А.9). Число степеней свободы для этого
выражения f1 = k - 1.
, nхi
- то же, что в формуле (А.9). Число степеней свободы для этого
выражения f1 = k - 1.
Для подсчета средней дисперсии всех экспериментальных точек относительно линий регрессии сначала находят дисперсию точек для каждой линии по формуле (А.2). При этом принимают
S2
= ![]()
где Ui = Uik - то же, что Ui в формуле (А.2) для данной серии испытаний;
![]() =
= ![]() - то же, что
- то же, что ![]() в формуле (А.2) для
данной серии испытаний;
в формуле (А.2) для
данной серии испытаний;
N = nсер - общее число образцов для данной серии при всех температурах испытаний. Формула (А.2) принимает вид:
|
|
(A.26) |
Примечание - Если проверялась гипотеза линейности или если при циклических испытаниях (в случае измерения критериев отказа в конце цикла) все отказы в каком-либо из режимов произошли только в одном - двух циклах, то дисперсию определяют по результатам вычисления дисперсий для каждого режима испытаний данной серии в соответствии с приложением Д. Если имеются сомнения в однородности дисперсий экспериментальных точек каждого режима испытаний данной серии, проводят проверку гипотезы однородности дисперсии в соответствии с приложением Е, а при обнаружении неоднородности дисперсий - проводят вычисления по приложению Е. При неодинаковом количестве образцов в различных режимах испытаний обработку результатов проводят в соответствии с приложением Е.
С несколько большей, но
допустимой долей погрешности можно подсчитать ![]() по упрощенной
формуле:
по упрощенной
формуле:
|
|
(A.27) |
где ![]() - то же, что
- то же, что ![]() в формуле (А.9) для
данной серии испытаний;
в формуле (А.9) для
данной серии испытаний;
nxi и ni – то же, что в формуле (А.4) для данной серии испытаний.
Формулу (А.27) применяют для предварительной оценки, если имеются существенные опасения в том, что вследствие непараллельности графиков дальнейшая обработка результатов всей совокупности испытаний по данному варианту нецелесообразна.
После определения дисперсий каждой серии находят среднюю дисперсию всех серий:
|
|
(A.28) |
Число степеней свободы здесь f2 = k(псер - 2).
После этого вычисляют дисперсионное отношение
|
|
(A.29) |
Полученные значения F сравнивают с табличным Fтa6л, взятым для необходимого уровня значимости, причем значение степеней свободы f2 и f1, вычисляют для знаменателя и числителя, как указано выше.
Графики будут считаться параллельными, если F ≤ Fтa6л.
После проверки гипотезы параллельности подсчитывают коэффициенты формулы (А.1). В качестве коэффициента а2 принимают значение а2, вычисленное по формуле (А.24).
Коэффициент а3 подсчитывают аналогично. Для этого сначала группируют данные так, чтобы выделить серии результатов испытаний и = f (С) при t = const и η = const. Затем определяют а3k1 для каждой серии [аналогично определению а3 в формулах (А.11) и (А.13)]:
|
a3 = (Σk1a3k1)/k1, |
(A.30) |
где k1 - число серий результатов испытаний при постоянной температуре и влажности и переменной концентрации (число испытательных температур, для которых имеются сгруппированные данные об испытаниях при различных концентрациях).
Аналогично определяют
коэффициент а4. Для определения коэффициента а4 сначала находят средние ![]() . Эти значения определяют по формулам, аналогичным формуле (А.15).
После этого определяют а4 по формуле, аналогичной формуле (А.16).
После подстановки полученных коэффициентов в формулу (А.1) можно, как и в варианте 1, вычислить средние
значения
. Эти значения определяют по формулам, аналогичным формуле (А.15).
После этого определяют а4 по формуле, аналогичной формуле (А.16).
После подстановки полученных коэффициентов в формулу (А.1) можно, как и в варианте 1, вычислить средние
значения ![]() при испытательных и
других требуемых значениях воздействующих факторов и построить графики
зависимостей Lcp от температуры,
концентрации и влажности агрессивной среды, затем проводят вычисления
дисперсий.
при испытательных и
других требуемых значениях воздействующих факторов и построить графики
зависимостей Lcp от температуры,
концентрации и влажности агрессивной среды, затем проводят вычисления
дисперсий.
Вычисления S, ![]() =
= ![]() проводят
также, как и для варианта 1 [формулы (А.18) - (А.20)], при этом в формулу
(А.20) вместо n1 необходимо подставить nik, где nik - общее число образцов, оставленных
для рассмотрения в данной серии сгруппированных результатов (при одинаковых
температуре, влажности и разных концентрациях или при одинаковых концентрации,
влажности и разных температурах, или при одинаковых температуре, концентрации и
разной влажности).
проводят
также, как и для варианта 1 [формулы (А.18) - (А.20)], при этом в формулу
(А.20) вместо n1 необходимо подставить nik, где nik - общее число образцов, оставленных
для рассмотрения в данной серии сгруппированных результатов (при одинаковых
температуре, влажности и разных концентрациях или при одинаковых концентрации,
влажности и разных температурах, или при одинаковых температуре, концентрации и
разной влажности).
А.3.4. Вариант 4 (рисунок А.4)
Дано
1-я серия: L= f(t°С) при С = const, η = const;
2-я серия: L = f(С) при одной или нескольких температурах и влажности;
3-я серия: L = f(η) при одной или нескольких температурах и концентрациях.
Известно, что lg L = f(lg С) или lg L = f(lg η) (вместо L в соответствии с 8.5 может быть подставлена скорость b2) имеет перегиб (коэффициент а3 или a4 в формуле (А.1) имеет два или более значений).
Вначале вычисляют параметры зависимостей в 1-й серии испытаний. При этом можно применять формулу, аналогичную (А.23) в варианте 3
|
Uxk = axk + a2kx, |
(A.31) |
Коэффициент а2k подсчитывают аналогично коэффициенту а2 в варианте 1. Например, для 1-й серии испытаний
|
|
(A.32) |
Значения ![]() , xik,
, xik, ![]() , a2k
аналогичные формуле (А.9), обозначены соответственно
, a2k
аналогичные формуле (А.9), обозначены соответственно ![]() , xk1,
, xk1, ![]() , a21
, a21
|
|
(A.33) |
Коэффициент aхk для 1-й серии испытаний (обозначенный ах1) подсчитывают по формуле:
|
|
(A.34) |
Коэффициент аxk для
значений концентрации и влажностей, отличных от значений в 1-й серии, вычисляют
подстановкой в формулу (А.31) значений ![]() и xik, полученных из соответствующих экспериментов
для различных концентраций и влажностей
и xik, полученных из соответствующих экспериментов
для различных концентраций и влажностей
|
|
(A.35) |
Определяя аxk для необходимых концентраций и
влажностей, при которых проводился эксперимент, можно вычислять средние
значения ![]() и L'хk при требуемых
температурах, концентрациях и влажностях (из числа концентраций и влажностей,
при которых проводился эксперимент):
и L'хk при требуемых
температурах, концентрациях и влажностях (из числа концентраций и влажностей,
при которых проводился эксперимент):
|
|
(A.36) |
U и L при
концентрациях и влажностях, при которых эксперимент не проводился,
рекомендуется определять графически расчетным методом. Для этого по данным
предыдущих вычислений строят графики зависимости U = f(y) при какой-либо температуре и
влажности, графически определяют значение ![]() при заданном у, после
чего по формуле (А.35) можно найти соответствующее значение коэффициента аxk для
данной концентрации, подставляя вместо
при заданном у, после
чего по формуле (А.35) можно найти соответствующее значение коэффициента аxk для
данной концентрации, подставляя вместо ![]() найденное значение
найденное значение ![]() . Можно воспользоваться чисто графическим методом, отложив
найденное значение
. Можно воспользоваться чисто графическим методом, отложив
найденное значение ![]() на графике и =
f(х) и проведя
через эту точку линию, параллельную ранее найденной зависимости и = f(x).
на графике и =
f(х) и проведя
через эту точку линию, параллельную ранее найденной зависимости и = f(x).
Дисперсии подсчитывают
отдельно для зависимости, полученной при концентрации и влажности 1-й серии
экспериментов и концентрациях и влажностях других серий. Для первой серии
экспериментов дисперсию экспериментальных точек относительной линии регрессии S2 = ![]() находят аналогично
дисперсии серии
находят аналогично
дисперсии серии ![]() в варианте 3 [формула (А.26)].
Затем вычисляют дисперсию средних значений линии регрессии в соответствии с
формулами (А.3)
и (А.4).
При этом принимают:
в варианте 3 [формула (А.26)].
Затем вычисляют дисперсию средних значений линии регрессии в соответствии с
формулами (А.3)
и (А.4).
При этом принимают:
N = nсеp1 - общее число образцов, оставленное для рассмотрения в 1-й серии испытаний;
b = bcep1 - коэффициент b, подсчитанный для 1-й серии.
Формулы (А.3) и (А.4) принимают вид:
|
|
(A.37) |
|
|
(A.38) |
Дисперсию средних
значений при концентрациях и влажностях, отличных от 1-й серии, вычисляют в
соответствии с формулами (А.3) и (А.4), но с учетом дополнительной дисперсии
среднего значения Uxk.
При этом принимают S2 = ![]() , подсчитанное для 1-й серии:
, подсчитанное для 1-й серии:
N = ncep1,
fst = ncep1 + ncep.k - 1
Формулы (А.3) и (А.4) принимают вид:
|
|
(A.39) |
|
|
(A.40) |
где nсep.k - общее число образцов, оставленных для рассмотрения в данной серии, отличной от 1-й;
bcep.k - коэффициент b для данной серии, отличной от первой.
Дано
L = f(t°С), L = f(С), L = f(η) при нескольких температурах, концентрациях и влажностях. Известно, что lg L = f(lg С) или lg L = f(lg η) (вместо L в соответствии с 8.5 может быть применена скорость b2) имеет перегиб (коэффициенты а3 или а4 в формуле (А.1) имеют два или более значений).
Сначала вычисления проводят аналогично варианту 3: вычисляют параметры зависимостей по формуле (А.23) для каждой серии испытаний при каждой из испытательных концентраций; проверяют гипотезу параллельности; подсчитывают коэффициенты формулы (А.23).
В качестве коэффициента а2к
для всех серий испытаний принимают ![]() по формуле (А.24).
Подсчет коэффициента а1k в
каждой серии испытаний производят (аналогично подсчету коэффициента ахк в варианте 4) по формуле:
по формуле (А.24).
Подсчет коэффициента а1k в
каждой серии испытаний производят (аналогично подсчету коэффициента ахк в варианте 4) по формуле:
|
|
(A.41) |
Здесь ![]() и xik были получены при вычислении коэффициентов а2k. Для подсчета
дисперсии учитывают результаты всех серий испытаний. В качестве дисперсии
экспериментальных точек относительно линии регрессии принимают среднюю
дисперсию всех серий S2 =
и xik были получены при вычислении коэффициентов а2k. Для подсчета
дисперсии учитывают результаты всех серий испытаний. В качестве дисперсии
экспериментальных точек относительно линии регрессии принимают среднюю
дисперсию всех серий S2 = ![]() по формуле (А.28).
по формуле (А.28).
Затем подсчитывают в
соответствии с формулами (А.3) и (А.4) дисперсию средних значений линий
регрессии ![]() , которую
можно принять одинаковой для всех серий.
, которую
можно принять одинаковой для всех серий.
Формулы (А.3) и (А.4) принимают вид:
|
|
(A.42) |
|
|
(A.43) |
где пk - общее число образцов, рассматриваемых при данной температуре и всех концентрациях и влажности.
Даны результаты
определения срока L конструкции или готового изделия в одном испытательном
режиме и зависимости L = f(toС, η, С), полученные при испытаниях образцов подобия во всех требуемых
режимах. По этим результатам рассчитывают срок L (включая
требуемые статистические показатели) для конструкции или готового изделия при
требуемых (рабочих) воздействующих факторах, используя коэффициенты зависимости
формулы (А.1), полученные на образцах
подобия. Для этого вычисляют в соответствии с А.2.1 для конструкции или готового
изделия срок L каждого образца, логарифмы сроков L(Uig), некорректированный и (при
необходимости) корректированный средний логарифмический срок ![]() .
.
Затем вычисляют для
конструкций или готового изделия средний логарифмический срок ![]() при требуемых
значениях воздействующих факторов:
при требуемых
значениях воздействующих факторов:
|
|
(A.43a) |
где а2, а3, а4 - коэффициенты, полученные при испытании образцов подобия;
xтр, хi, утр, yi, zтр, zi - то же, что в формулах (А.4) и (А.15).
Вычисляют дисперсию результатов испытаний конструкции или готового изделия при испытательном режиме:
|
|
(A.43б) |
где пig - количество образцов при испытаниях.
Вычисляют для конструкции или готового изделия дисперсию средних значений поверхности отклика при требуемых значениях температуры, влажности, концентрации агрессивной среды:
|
|
(A.43в) |
|
|
(A.43г) |
|
bg = b + 1/nig, |
(A.43е) |
где S, fs, b - значения, полученные при испытании образцов подобия.
Далее вычисления проводят в соответствии с требованиями А.2.5 - А.2.7.
ПРИЛОЖЕНИЕ
Б
(обязательное)
Методы определения коэффициента ускорения испытаний и срока службы L сравнением
скоростей изменения значений параметров-критериев отказа
Б.1. Метод применяют в случаях, когда математическая функция зависимости величины критерия отказа от времени воздействия испытательных факторов может быть представлена в виде прямой линии до момента достижения критического значения критерия отказа, т.е. может быть выражена формулой:
|
f(П) = b1 - b2τ, |
(Б.1) |
где П - значение критерия отказа;
f(П) - соответствующая математическая функция П (например, во многих случаях f(П) = lg П);
τ - длительность воздействия агрессивной среды при испытаниях;
b1 и b2 - величины, постоянные для данного режима испытаний и вида образца (b2 - скорость изменения f(П) от времени воздействия агрессивной среды). Схематическое изображение вариантов зависимости по формуле (Б.1), для которых может быть применен настоящий метод, приведено на рисунках Б.1 и Б.2, причем для варианта, указанного на рисунке Б.2, здесь и далее под зависимостью по формуле (1) понимают участок 2.
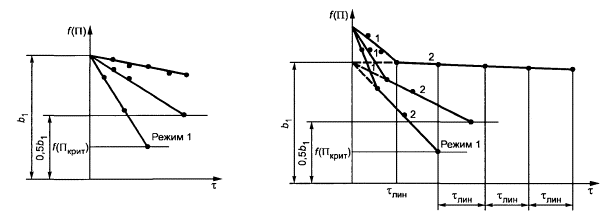
|
Рисунок Б.1 - Скорость изменения значения параметра в процессе испытания, неизменная |
Рисунок Б.2 - Скорость изменения значения параметра в процессе испытания, претерпевающая одно изменение |
Б.2. В каждом испытательном режиме, выбранном по разделу 8, определяют зависимость критерия отказа от времени воздействия испытательных факторов, при этом зависимость должна быть получена не менее чем по трем экспериментальным точкам, каждая из которых должна быть получена в результате испытаний не менее четырех образцов. Если по данному виду основного испытательного воздействия используют режимы испытаний, то для наиболее слабого режима эта зависимость должна быть получена не менее чем по пяти экспериментальным точкам.
Б.3. При выборе величин воздействующих факторов и времени испытаний в каждой серии испытаний по разделу 8 руководствуются следующим:
а) испытание в самом жестком режиме данной серии проводят до снижения среднего значения критерия отказа до критического значения. При неразрушающих измерениях критерия отказа рекомендуется проводить испытания до отказа каждого образца;
б) продолжительность испытания в промежуточном режиме должна быть не менее времени, необходимого для того, чтобы f(П) стало равным 0,5b1 (рисунки Б.1 и Б.2);
в) продолжительность испытания в самом слабом режиме должна быть не менее продолжительности испытания в промежуточном режиме, при этом, для варианта по рисунку 2 интервалы времени между соседними экспериментальными точками должны быть не менее τлин (рисунок Б.2). Значение испытательного воздействия в самом слабом режиме рекомендуется выбирать возможно более близким к рабочим значениям воздействующего фактора по разделу 5 настоящего стандарта;
г) планы эксперимента в части выбора видов и значений воздействующих факторов выбирают по приложению А.
Б.4. По результатам испытаний для каждого из режимов испытаний определяют среднюю скорость b2 методом наименьших квадратов с определением дисперсии и нижнего доверительного предела для среднего.
Б.5. Используя определенные по Б.4 значения b2, вычисляют по приложению Б.2 коэффициенты а2, а3, а4 формулы (А.1).
Б.6. Определяют коэффициент ускорения и (или) срок L.
Б.6.1. Определяют коэффициент ускорения Куск в соответствии с 5.4.
Б.6.2. Для критического
или заданного значения критерия отказа Пкр
определяют среднее значение срока Li и ![]() в каждом режиме:
в каждом режиме:
|
Li = (f(Пкр) - b1)/b2i, |
(Б.1а) |
|
|
(Б.1б) |
где b2 - то же, что b2 по формуле (Б.5);
bt - по формуле (Б.13).
Б.6.3. Определяют
дисперсию логарифмов скоростей b2 в каждом режиме ![]() .
.
Эта дисперсия определяет
дисперсию значений Ui относительно среднего значения ![]() , для каждого
режима испытаний и равна
, для каждого
режима испытаний и равна ![]() по приложению Д
по приложению Д
|
|
(Б.1в) |
Б.6.4. Дальнейшую
обработку результатов для прогноза срока L при требуемых (эффективных)
значениях основных воздействующих факторов и расчета погрешностей прогноза
проводят по приложениям
А и Д,
используя вычисленные значения ![]() и
и ![]() .
.
Б.6.5. Для прогнозирования изменения значений параметра-критерия отказа и погрешностей прогноза производят прогнозирование величин скорости изменения значения параметра-критерия отказа и погрешности прогноза следующим образом.
Б.6.5.1. Определяют коэффициент а1 по приложению А для случая, когда U - lg b2.
Б.6.5.2. Определяют
среднюю скорость b2тр
и ее среднее логарифмическое значение ![]() = lgb2тp при требуемых (эффективных)
значениях основных воздействующих факторов в соответствии с приложением А.
= lgb2тp при требуемых (эффективных)
значениях основных воздействующих факторов в соответствии с приложением А.
Б.6.5.3. Определяют
дисперсию логарифмов скоростей ![]() (см. А.2.4)
(см. А.2.4)
|
|
(Б.1г) |
где ![]() - по формуле (Б.24);
- по формуле (Б.24);
b - по формуле (А.4).
Б.6.5.4. Определяют верхний доверительный предел UbР, для средних логарифмических значений скорости b2тр при заданной доверительной вероятности Р*
|
|
(Б.1д) |
где t - то же, что и в формуле (А.5)
Б.6.5.5. Определяют верхний доверительный предел Ubp (при заданной доверительной вероятности Р*) для логарифма скорости b2тр при заданной вероятности безотказной работы или безотказного хранения Р (верхний толерантный предел)
|
|
(Б.1г) |
где zP, Uα - то же, что в формуле (А.6).
Б.6.5.6. Определяют верхний доверительный предел для средней скорости b2тр(b2P*тр) и верхний толерантный предел b2Pтр.
|
|
(Б.1ж) |
Б.6.5.7. Определяют среднее значение f(П)тр, нижний доверительный предел для среднего f(П)P*тр и нижний толерантный предел f(П)Pтр для требуемого момента времени τ по формулам:
|
|
(Б.1з) |
|
|
(Б.1и) |
|
|
(Б.1к) |
Б.6.5.8. По определенным значениям f(П)тр вычисляют значение Птр и его нижние пределы (доверительный для среднего и толерантный) при требуемых (эффективных) значениях основных воздействующих факторов.
Б.7. Среднюю скорость b2 в каждом режиме (пункт Б.4) определяют в последовательности, приведенной ниже.
Б.7.1. Вычисляют средние
значения ![]() для каждого периода
времени измерения параметра-критерия отказа (для каждой экспериментальной точки
по пункту Б.2)
для каждого периода
времени измерения параметра-критерия отказа (для каждой экспериментальной точки
по пункту Б.2)
|
|
(Б.2) |
где f(П)изм - значения f(П) для каждого образца при данном времени измерения;
п'изм - число образцов, проверенных при окончании данного периода времени измерения.
Б.7.2. При необходимости корректируют результаты испытаний, исключая из рассмотрения образцы с резко выделяющимися значениями f(П). Резко выделяющиеся значения оценивают по приложению Г, подставляя в соответствующие формулы значения f(П) вместо указанных в приложении Г значений U. Затем вычисляют среднее корректированное значение f(П)изм:
|
|
(Б.3) |
где пизм - составленное для рассмотрения число образцов, проверенных при данном времени измерения.
Б.7.3. Определяют средние
значения ![]() и
и ![]()
|
|
(Б.4) |
где преж число периодов времени измерений в данном режиме (например, для режима 1, рисунок Б.1, преж = 4; для режима 1, рисунок Б.2, преж = 3);
τреж - время воздействия испытательной среды до момента данного измерения (для начального измерения по рисунку Б. 1 τреж = 0).
Б.7.4. Находят среднее значение скорости bг по формуле:
|
|
(Б.5) |
Б.7.5. Определяют коэффициент:
|
|
(Б.6) |
Б.7.6. Если вызывает сомнение соответствие экспериментальных данных формуле (Б.1), проверяют гипотезу линейности. Если гипотеза линейности не принимается, методику испытаний по данному приложению применять нельзя.
Гипотезу линейности проверяют следующим образом:
а) определяют ![]() :
:
|
|
(Б.7) |
б) определяют ![]() :
:
|
|
(Б.8) |
в) вычисляют дисперсионное отношение:
|
|
(Б.9) |
г) полученное значение F сравнивают с Fтабл, взятым для необходимого уровня значимости, причем в качестве значений степеней свободы f(2) и f(1) принимают знаменатели формул (Б.7) и (Б.8) соответственно.
Гипотезу линейности не принимают, если Fтабл < F.
Б.7.7. Если экспериментальные данные образуют зависимости, соответствующие рисунку Б.2, сравнивают коэффициенты b1 для всех режимов при помощи дисперсионного анализа с использованием критерия Фишера.
Если различия между коэффициентами существенны, методику испытаний по данному приложению применять нельзя.
Проверку осуществляют следующим образом:
а) определяют для каждого
режима ![]() :
:
|
|
(Б.10) |
где обозначения те же, что в формуле (Б.15);
б) определяют среднюю
дисперсию режимов ![]() :
:
|
|
(Б.11) |
Число степеней свободы здесь f(2) = Σпреж(пi);
в) определяют дисперсию средних значений b1 для всех режимов
|
|
(Б.12) |
|
|
(Б.13) |
Число степеней свободы здесь f(1) = преж - 1;
г) вычисляют дисперсионное отношение
|
|
(Б.14) |
Полученное значение сравнивают с Fтабл, взятым для необходимого уровня значимости, причем значение степеней свободы вычисляют для числителя и знаменателя формулы (Б.14).
Если Fbl ≥ Fтa6л, различия между коэффициентами b1 считают существенными.
Б.8. Дисперсии и нижние доверительные пределы для средней скорости b2 (Б.4) определяют для каждого режима в приведенной ниже последовательности.
Б.8.1. Определяют дисперсию значений f(П) для данного режима:
|
|
(Б.15) |
где f(П)изм - то же, что в формуле (Б.2);
пизм - то же, что в формуле (Б.3);
преж - то же, что в формуле (Б.4);
ni - общее число образцов, оставленных для рассмотрения в данном режиме;
f'(П)изм – значение f(П), вычисленное для каждого времени измерения τ по формуле (Б.1) с подстановкой значений b1 и b2, определенных формулами (Б.5) и (Б.6).
Б.8.2. Определяют дисперсию значений b2 данного режима:
|
|
(Б.16) |
Число степеней свободы
для ![]() :
:
![]()
Б.8.3. Определяют нижний доверительный предел b2p, для среднего значения b2 по заданной доверительной вероятности Р*
|
|
(Б.17) |
где t - распределение доверительных отклонений в малой выборке (распределение Стьюдента), определяемое по статистическим таблицам для заданного уровня доверительной вероятности Р* и числа степеней свободы tSb2. Для самого слабого режима b2P, должна быть значимо больше нуля.
Б.9. Нижние доверительные границы для среднего значения и нижнюю толерантную границу коэффициента ускорения (9.4) определяют следующим образом:
а) определяют среднюю дисперсию коэффициентов b2
|
|
(Б.18) |
где Sb2 - по формуле (Б.16);
т1 - общее число испытательных режимов;
б) определяют среднюю дисперсию логарифмов коэффициентов b2:
|
|
(Б.19) |
|
|
(Б.20) |
число степеней свободы
для ![]() ,
,
|
|
(Б.21) |
в) определяют дисперсию ![]() средних значений
средних значений ![]() относительно
соответствующих точек поверхности отклика:
относительно
соответствующих точек поверхности отклика:
|
|
(Б.22) |
где ![]() - логарифм средней скорости b2 в каждом
режиме испытаний, определенный по Б.7.4;
- логарифм средней скорости b2 в каждом
режиме испытаний, определенный по Б.7.4;
![]() - логарифм b2, подсчитанный по
формуле (А.1) для каждого режима
испытаний;
- логарифм b2, подсчитанный по
формуле (А.1) для каждого режима
испытаний;
т1 - то же, что в формуле (Б.18);
k - число серий испытаний.
Число степеней свободы
для ![]() :
:
|
|
(Б.23) |
г) определяют общую
дисперсию ![]() , экспериментальных
точек относительно вычислительной поверхности
, экспериментальных
точек относительно вычислительной поверхности ![]() = S no A.2.3)
= S no A.2.3)
|
|
(Б.24) |
д) определяют дисперсию ![]() логарифма
коэффициента ускорения испытаний по А.2.4;
логарифма
коэффициента ускорения испытаний по А.2.4;
е) определяют нижние доверительные границы среднего логарифмического и логарифма (при заданной вероятности безотказной работы) коэффициента ускорения, а также соответствующие значения коэффициента ускорения по А.2.5 и А.2.6).
ПРИЛОЖЕНИЕ
В
(обязательное)
Определение показателей надежности и коэффициентов ускорения испытаний при
переменных эксплуатационных значениях воздействующих факторов
8.1. Определение показателей надежности и коэффициентов ускорения испытаний при переменных эксплуатационных значениях воздействующих факторов по требованиям настоящего приложения проводят, если известны значения этих факторов (температура, влажность и концентрация среды) и параметры их статистического распределения за период наблюдений не менее пяти лет.
Определение показателей надежности и коэффициентов ускорения проводят по требованиям приложения А с дополнениями, указанными ниже.
8.2. Эффективные значения Тэ, Сэ, η, [или хтр, утр, zтр по формуле (А.4)] определяют по В.2.1 - В.2.3. Значения воздействующих факторов (температура, концентрация, влажность) и значения х, у, z при данном наблюдении обозначены в формулах соответственно: ТН, СН, ηН, и хН, уН, zН, kН - количество значений данного воздействующего фактора при периодических наблюдениях.
8.2.1. Значения параметров, определяемые температурой:
|
|
(В.1) |
или
|
|
(В.2) |
|
а2 = В' = B/2,303 = Еэфф/2,303R = Еэфф/4,575; |
(В.3) |
где Еэфф - эффективная энергия активации процесса возникновения отказа,
R - универсальная газовая постоянная.
8.2.2. Значения параметров, определяемые влажностью воздуха:
|
|
(В.4) |
η = 10
или
|
|
(В.5) |
8.2.3. Значения параметров, определяемые концентрацией агрессивной среды:
|
|
(В.6) |
СЭ = 10
или
|
|
(В.7) |
8.3. При подсчете коэффициента по формулам (А.4) и (А.4а) дополнительно прибавляют величину
|
|
(В.8) |
где ![]() ,
, ![]() ,
, ![]() - дисперсии
совокупности значений хН, уН, zH.
- дисперсии
совокупности значений хН, уН, zH.
Если не имеется данных о
значениях ![]() ,
, ![]() ,
, ![]() , вычисленных по данным каждого наблюдения,
допускается определять эти значения по формулам:
, вычисленных по данным каждого наблюдения,
допускается определять эти значения по формулам:
|
|
(В.9) |
где ![]() ,
, ![]() ,
, ![]() - дисперсии совокупности значений ТH, СH, ηH.
- дисперсии совокупности значений ТH, СH, ηH.
ПРИЛОЖЕНИЕ
Г
(обязательное)
Методы исключения резко выделяющихся значений результатов испытаний
В качестве метода исключения применяют критерий Ирвина.
Г.1. Определяют некорректированный средний логарифмический срок L при каждом испытательном режиме:
|
|
(Г.1) |
где Ui = lg L, L - значение срока L для каждого образца в данном режиме;
пiс - число образцов, испытывающихся в данном испытательном режиме.
Вычисляют некорректированную дисперсию логарифмов сроков при каждом испытательном режиме:
|
|
(Г.2) |
Г.3. Полученные значения U располагают в ряд Ul, U2, И3, … Un по степени возрастания значения U (вариационный ряд).
Г.4. Проверяют сомнительные значения на одном или двух краях ряда, составленного по Г.3. Проверку начинают от края ряда и проверяют поочередно каждое следующее (по направлению к середине ряда) сомнительное значение.
Г.5. Для проверки вычисляют функцию λкс:
|
λkc = (Ukc - U(k-1)c)/Sic; |
(Г.3) |
где Ukc - вызывающее сомнение значение логарифма срока L;
U(k-l)c - следующее от края ряда значение логарифма срока L;
k - номер по порядку от края ряда.
Г.6. Сравнивают полученные значения λкс с приведенными в таблице Г.1 значениями Кта6л. Если хотя бы для одного вызывающего сомнение значения логарифма срока L (Ukc) λкс больше λтабл, в расчет не принимают все вызывающие сомнения значения сроков Ukc от края ряда до Ukc включительно.
Г.7. Проверку продолжают до тех пор, пока не будут получены значения λкс ≤ λтабл.
Таблица Г.1
Значения функции λта6л при нормальном распределении
|
nic |
Значения λта6л для исключения резко выделяющихся значений при доверительной вероятности |
nic |
Значения λта6л для исключения резко выделяющихся значений при доверительной вероятности |
||
|
95 % |
99 % |
95 % |
99 % |
||
|
5 |
1,9 |
2,4 |
50 |
1,1 |
1,6 |
|
10 |
1,5 |
2,0 |
100 |
1,0 |
1,5 |
|
20 |
1,3 |
1,8 |
400 |
0,9 |
1,3 |
|
30 |
1,2 |
1,7 |
1000 |
0,8 |
1,2 |
ПРИЛОЖЕНИЕ
Д
(обязательное)
Проверка гипотезы линейности
Для проверки гипотезы
линейности сравнивают дисперсии средних значений ![]() относительно линий
регрессий со средней дисперсией экспериментальных точек относительно средних
значений
относительно линий
регрессий со средней дисперсией экспериментальных точек относительно средних
значений ![]() . Проверку проводят отдельно для каждой серии
испытаний.
. Проверку проводят отдельно для каждой серии
испытаний.
Средневзвешенную
дисперсию ![]() экспериментальных
точек относительно средних для них значений
экспериментальных
точек относительно средних для них значений ![]() вычисляют по
формулам:
вычисляют по
формулам:
|
|
(Д.1) |
|
|
(Д.2) |
где fi - степень свободы для данного режима, fi = ni - 1;
f4k - по формуле (Д.4);
Ui и
![]() - то же, что в
формуле (А.2)
и (А. 15)
соответственно;
- то же, что в
формуле (А.2)
и (А. 15)
соответственно;
пi - то же, что в формуле (А.4);
nxj - то же, что в формуле (А.9) [вместо nxi - при необходимости подставляют nyi или nzi, см. формулу (А.12)].
Если в случае измерения
параметров-критериев отказа в конце цикла или заданного интервала времени между
измерениями (далее - цикла) все отказы в каком-либо из режимов произошли только
в одном или двух циклах, то дисперсию для данного режима ![]() вычисляют по формуле:
вычисляют по формуле:
|
|
(Д.3) |
где ΔU - логарифм длительного цикла, после которого были обнаружены отказы;
пi - то же, что в формуле (А.4);
nu - большее число отказов, обнаруженное после одного из двух циклов (если после каждого из двух циклов обнаружено одинаковое число отказов, пц = 0,5 ni если все отказы обнаружены после одного цикла пи = пi);
zp - выбирают по статистическим справочникам для максимально приближенного к 1.
Число степеней свободы
для ![]() определяют по формуле
определяют по формуле
|
f4k = Σnxi(ni - 1), |
(Д.4) |
Если после проверки по приложению
В не проводилось исключение резко выделяющихся значений, вычисления ![]() по формуле (Д.2) не
проводят, так как в этом случае
по формуле (Д.2) не
проводят, так как в этом случае ![]() =
= ![]() по приложению В.
Дисперсию
по приложению В.
Дисперсию ![]() средних значений Ui относительно соответствующих значений линии регрессии
вычисляют по формуле
средних значений Ui относительно соответствующих значений линии регрессии
вычисляют по формуле
|
|
(Д.5) |
Число степеней свободы здесь:
|
f3k(1) = nxi - 2, |
(Д.6) |
где ![]() - то же, что в
формуле (Б.2);
- то же, что в
формуле (Б.2);
nxi, ni - то же, что в формуле (Д.2).
После этого вычисляют дисперсионное отношение:
|
|
(Д.7) |
Полученные значения сравнивают с Fтабл, взятым для необходимого уровня значимости, причем значения степеней свободы f3k(1) и f4k(2) вычисляют для числителя и знаменателя формулы (Д.7) как указано выше.
Гипотезу линейности не
принимают, если Fтабл
< F и при этом экспериментальные
значения ![]() располагаются
относительно линии регрессии таким образом, что образуют явно выраженный изгиб
(см. рисунок Д. 1).
располагаются
относительно линии регрессии таким образом, что образуют явно выраженный изгиб
(см. рисунок Д. 1).
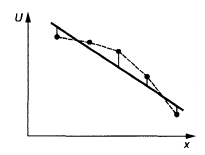
Рисунок Д.1 - Пример неприемлемости гипотезы линейности при Fтабл < F
В этом случае выполняют требования 9.3 настоящего стандарта. Допускается проводить обработку результатов по вариантам 4 и 5 приложения А.
Гипотезу линейности
принимают, если Fтабл
≥ F
или если Fтабл
< F, но при этом экспериментальные
значения ![]() располагаются относительно
линии регрессии хаотически (например, на рисунке Д.2).
располагаются относительно
линии регрессии хаотически (например, на рисунке Д.2).
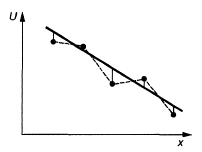
Рисунок Д. 2 - Пример приемлемости гипотезы линейности при Fтабл < F
Для вычисления дисперсии экспериментальных точек относительно вычисленной поверхности вместо формул (Б.20) или (Б.18) удобнее применять формулу:
|
S2 = [Σk(f4k× |
(Д.8) |
где fs - по формуле (А.17).
ПРИЛОЖЕНИЕ
Е
(обязательное)
Обработка экспериментальных данных при неравноточных измерениях
Б.1 Общие положения
Е.1.1. Обработку экспериментальных данных при неравноточных измерениях проводят по приложениям А и Г с указанными ниже изменениями.
Е.1.2. Изменения учитывают неравноточность вследствие неоднородности дисперсий или (и) различия количества образцов в разных режимах испытаний. Учет неравноточности проводят преобразованием некоторых из установленных в приложениях Б и Д формул путем введения в них коэффициента неравноточности D.
Преобразованные формулы и значения коэффициента D приведены в таблице Е.1.
Е.1.3. Неоднородность дисперсий учитывают в случае, если проверкой по Е.2 выявлено, что дисперсии точек в разных режимах неоднородны.
Е.1.4. Различие количества образцов в разных режимах испытаний рекомендуется учитывать для данной серии испытаний только в случае, когда количества испытательных образцов в режимах испытаний этой серии различаются (в т.ч. из-за исключения резко выделяющихся значений) более чем на 20 %, а заданная доверительная вероятность обработки результатов больше 0,99.
Е.1.5. Различие количества образцов и неоднородность дисперсий учитывают одновременно при выполнении условий по Е.1.3 и Е.1.4.
Е.1.6. Дисперсионные отношения ωik и ωk, входящие в коэффициент D по таблице Е. 1, вычисляют по формулам (Е.1) и (Е.2). При этом ωik вычисляют для каждого режима испытаний данной серии; ωk вычисляют для каждой серии при испытаниях по вариантам 3 и 5 приложения А:
|
ωik = |
(Е.1) |
|
ωk = |
(Е.2) |
Примечание - Если проводят только три серии испытаний для получения зависимостей L = f(T), L = f(C) и L = f(η), то вместо обозначения ωik применяют соответственно обозначения ωix, ωiy, ωiz.
Е.2. Проверка гипотезы однородности дисперсий
Е.2.1. Для проверки гипотезы однородности дисперсий величины U при различных значениях х, у и z используют критерий Барлета. Проверку проводят отдельно для каждой серии испытаний. Ниже приведены способ проверки для серии испытаний при различных х при неизменных у и z. Аналогично проводят проверку для других серий.
Е.2.2. Находят величину критерия Барлета (Б):
|
|
(Е.3) |
|
|
(Е.4) |
Полученное значение Б сравнивают с величиной функции χ2, взятой из статистических таблиц для вероятности 1 - Р* и числа степеней свободы:
|
fБ = nxi - 1 |
(Е.5) |
где Р* - заданная доверительная вероятность.
Если Б ≤ χ2, то дисперсии считают однородными. Если Б > χ2, то дисперсии считают однородными, а обработку экспериментальных данных проводят с учетом изменений, приведенных в Е.1.
Таблица E.1
Выбор преобразования формул для определения параметров при обработке результатов испытаний при неравноточных измерениях
|
Номер формулы по приложению Е |
Обозначение параметра |
Номер формулы по приложению А |
Равноточные изменения (формулы по приложениям А и Д) |
Неравноточные измерения |
|||
|
Формулы |
Значение коэффициента |
||||||
|
при однородных дисперсиях, с учетом различия количества образцов |
при неоднородных условиях |
||||||
|
Без учета различия количества образцов |
С учетом различия количества образцов |
||||||
|
Е.6 |
|
А.9 |
|
|
1 |
ωik |
ωik |
|
Е.7 |
|
А.9 |
|
|
ni |
ωik |
niωik |
|
Е.8 |
a2 |
А.10 |
|
|
пi |
ωik |
niωik |
|
Е.9 |
|
A.11 |
|
|
1 |
ωik |
ωik |
|
Е.10 |
|
A.11 |
|
|
пi |
ωik |
niωik |
|
Е.11 |
|
А.12 |
|
|
1 |
ωik |
ωik |
|
Е.12 |
zik |
А.12 |
|
|
ni |
ωik |
niωik |
|
Е.13 |
a3 |
А.13 |
|
|
ni |
ωik |
niωik |
|
Е.14 |
A4 |
А.14 |
|
|
ni |
ωik |
niωik |
|
Е.15 |
|
А.32 |
|
|
1 |
ωik |
ωik |
|
Е.16 |
|
А.32 |
|
|
ni |
ωik |
niωik |
|
Е.17 |
a21 |
А.33 |
|
|
ni |
ωik |
niωik |
|
Е.18 |
|
Д.5 |
|
|
1 |
ωik |
niωik |
|
Е.19 |
|
А.26 |
|
|
1 |
ωik |
ωik |
|
Е.20 |
b |
А.4 А.20 |
|
|
ni |
ωik |
niωik |
|
Е.21 |
|
А.24 |
|
|
ni |
ωik |
niωik |
|
Е.22 |
|
А.25 |
|
|
ncep/Σkncep |
ωk |
ωk ncep/Σkncep |
|
Е.23 |
bcep1 |
А.38 |
|
|
1 |
ωil |
ωil |
|
Е.24 |
bcep.k |
А.40 |
|
|
1 |
ωik |
ωik |
|
Е.25 |
b |
А.43 |
|
|
1 |
|
|
Обозначения величин:
m1,
(формулы 20 и 25) - общее число испытательных режимов; ωil (формула 23) - значение ωik
для 1-й серии испытаний; nxik (формула
24) - количество режимов испытаний в данной серии, отличной от 1-й серии; ![]() (формулы 20 и 25) - в
первом члене формулы применяют обозначение ωik, во втором и последующих членах формулы -
соответственно ωix, ωiy, ωiz по примечанию к Е.1.6.
(формулы 20 и 25) - в
первом члене формулы применяют обозначение ωik, во втором и последующих членах формулы -
соответственно ωix, ωiy, ωiz по примечанию к Е.1.6.
ПРИЛОЖЕНИЕ
Ж
(обязательное)
Методы определения долговечности лакокрасочных покрытий при ускоренных
испытаниях в агрессивных газообразных средах
Ж.1. Общие положения
Долговечность лакокрасочных покрытий (далее - покрытий) определяют:
- для защитных покрытий:
по изменению электрического сопротивления (метод 1),
по отслаиванию покрытия от защищаемого металла (метод 2),
по комплексу критериев отказа (электрического сопротивления покрытия, относительного уменьшения толщины металлического подслоя под покрытием, тока гальванической пары «защищаемый металл - медь») (метод 3);
- для электроизоляционных покрытий - по изменению уровня электрических параметров покрытия до установленного критического значения (метод 4).
Метод 1 применяют для покрытий, электрическое сопротивление которых изменяется в процессе испытаний. Начальное удельное электрическое сопротивление покрытий должно быть не менее 108 Ом·см.
Метод 2 применяют для покрытий, электрическое сопротивление которых не изменяется в процессе испытаний и отказ которых вызывается отслаиванием покрытий от защищаемого металла (например, для перхлорвиниловых покрытий). Критическое значение критерия отказа - отслаивание на (35 ±5)% поверхности покрытия, определяемое визуально. Допускается применять критерии отказа, установленные для метода 1 ГОСТ 9.083.
Метод 3 применяют при исследовании покрытий с целью изучения механизма отказа.
Настоящее приложение применяют совместно с ГОСТ 9.083.
Ж.2. Определение долговечности покрытий по изменению их электрического сопротивления (метод 1).
Ж.2.1. Требования к образцам
Ж.2.1.1. Образцы должны соответствовать требованиям ГОСТ 9.083, раздел 2 (в части формы, размеров, испытуемых материалов), а также 5.5, 5.7, Ж.2.1.2 и Ж.2.1.5.
Применяют прямоугольные образцы, взвешивание перед окрашиванием не проводят, края образцов защищают стойким в данной среде герметиком.
Ж.2.1.2. Покрытие не должно иметь сквозных пор и пузырей.
Отсутствие пористости проверяют по ГОСТ 9.083, раздел 2.
Вместо воронки допускается использовать стеклянный цилиндр диаметром 50 мм и высотой 40 - 80 мм, который приклеивают, как и воронку, пластилином или герметиком в соответствии с требованиями ГОСТ 9.083, раздел 4. При использовании герметика после измерения электрического сопротивления цилиндр не снимают и используют в дальнейших испытаниях.
Ж.2.1.3. Для измерений электрического сопротивления прикрепляют соединительный провод на весь период испытаний или на время одного измерения. В первом случае изолированный провод припаивают к краю образца перед нанесением покрытия, затем наносят покрытие, место контакта дополнительно защищают стойким к агрессивной среде герметиком. Во втором случае перед каждым измерением край образца зачищают от герметика и покрытия, затем присоединяют провод и проводят измерение. После измерений край снова защищают герметиком.
Ж.2.1.4. Методы подготовки поверхности, способы нанесения покрытия, режимы сушки и отверждения должны соответствовать требованиям, предъявляемым к каждому виду покрытия или технологии окрашивания изделия.
Ж.2.1.5. Число образцов, требуемое для измерений в каждом испытательном режиме, устанавливают в зависимости от предполагаемого числа съемов, возможности определения нескольких показателей на одном образце при одном съеме или на одних и тех же образцах в процессе всего режима испытаний. Каждое значение показателя определяют не менее чем на 10 образцах.
Ж.2.2. Требования к средствам испытаний
Испытательная камера, отвечающая требованиям раздела 6.
Толщиномер типов ВТ-30НЦ, ВТ-10НЦ.
Тераомметр типа МОМ-4 или других типов.
Стойки или штативы для размещения образцов, изготовленные из материалов, стойких к воздействию соответствующих газообразных агрессивных сред.
Воронки и цилиндры стеклянные диаметром 50 мм по ГОСТ 25336.
Химические реактивы квалификации х. ч., ч. д. а., ч.
Пластилин.
Ж.2.3. Подготовка к испытаниям
Ж.2.3.1. Подготовка испытательного оборудования и предварительная обработка режима - по 8.1.
Ж.2.3.2. После проверки на отсутствие пористости по Ж.2.1.1 перед испытаниями образцы выдерживают в нормальных климатических условиях испытаний по ГОСТ 15150 не менее 12 ч и проводят визуальный осмотр.
Ж.2.3.3. Образцы помещают в испытательную камеру вертикально, чтобы испытательная среда имела равномерный доступ ко всем образцам.
Ж.2.4. Проведение испытаний
Ж.2.4.1. Испытания образцов - нециклические. На образцы одновременно воздействуют температура, влажность и агрессивный агент.
Ж.2.4.2. При испытаниях периодически, в соответствии с требованиями 8.14, измеряют электрическое сопротивление покрытия каждого образца. Электрическое сопротивление покрытия определяют по ГОСТ 9.083, пункт 2.1.1, при этом проводят только одно измерение спустя 2 мин после заливки воды. После измерения сопротивления воронку (или цилиндр), приклеенную пластилином, снимают и при отсутствии отказа испытания образца продолжают, предварительно защитив место крепления соединительного провода в соответствии с Ж.2.1.2. Остатки пластилина с образца не удаляют, если при температуре испытаний пластилин не затекает на испытуемую поверхность.
Ж.2.4.3. Испытания в камере продолжают до отказа покрытия всех образцов.
Допускается проводить испытания до отказа части образцов (см. 8.17 и приложение Б).
Ж.2.4.4. Критическим значением критерия отказа является значение приведенного электрического сопротивления покрытия в предельном состоянии (приведенное сопротивление разрушения) Rпр.кр. Для его определения проводят испытания по Ж.2.4.2 в одном из наиболее жестких режимов до отказа всех образцов и находят зависимость электрического сопротивления каждого образца от продолжительности испытаний.
Далее вычисляют приведенное сопротивление покрытия Rnр и определяют приведенное сопротивление Rпр.кр по ГОСТ 9.083, раздел 4.
Ж.2.4.5. Испытания образцов в других режимах заканчивают, когда Rnр каждого образца уменьшается до средней величины Rпр.кр, что является показателем появления сквозных пор в покрытии вследствие его разрушения.
Ж.2.5. Обработка результатов
Ж.2.5.1. Обработка результатов - по разделу 6 и приложениям А - Д, настоящего стандарта, а также разделу 4 ГОСТ 9.083.
Ж.3. Определение долговечности покрытия по отслаиванию (метод 2)
Ж.3.1. Требования к образцам - по ГОСТ 9.083, раздел 2 и пунктам 5.5, 5.7, Ж.2.1.2, Ж.2.1.4, Ж.2.1.5 настоящего приложения.
При использовании критерия отказа для метода 1 по ГОСТ 9.083 образцы готовят в количестве, установленном для этого метода.
При испытаниях покрытий, свойства которых в отношении применения данного метода неизвестны, образцы должны соответствовать требованиям Ж.2.1.
Ж.3.2. Требования к средствам испытаний - по Ж.2.2.
При использовании критерия отказа для метода 1 по ГОСТ 9.083 дополнительно применяют:
- весы лабораторные по ГОСТ 24104, класс точности 1;
- колбы плоскодонные вместимостью 250 - 4000 см3 по ГОСТ 25336;
- бюретки по ГОСТ 25336;
- резинки чернильные.
Ж.3.3. Подготовка к испытаниям - по Ж.2.3.
Ж.3.4. Проведение испытаний
Ж.3.4.1. Испытания образцов - нециклические. На образцы одновременно воздействуют температура, влажность и агрессивный агент.
Ж.3.4.2. При испытаниях образцы периодически осматривают в соответствии с требованиями 8.13. При обнаружении мест отслаивания определяют площадь отслаивания (например, наложением на образец пластины с нанесенной на нее размерной сеткой).
При отсутствии отказа испытания образцов продолжают.
Ж.3.4.3. При применении критериев отказа, установленных для метода 1 по ГОСТ 9.083, определяют среднюю адгезию, среднюю потерю массы и показатель подпленочной коррозии в предельном состоянии в соответствии с требованиями ГОСТ 9.083, раздел 2.
Ж.3.4.4. Испытания в камере продолжают до наступления отказа покрытия всех образцов.
Допускается проводить испытания до отказа части образцов (см. 8.17 и приложение Б).
Ж.3.5. Обработка результатов - по разделу 9 и приложениям А - Д.
Ж.4. Определение долговечности покрытия по изменению комплекса параметров-критериев отказа (метод 3)
Ж.4.1. Требования к образцам
Ж.4.1.1. Образцы для испытаний должны соответствовать требованиям 5.5, 6.7 и Ж.2.1.2, Ж.2.1.5, Ж.4.1.2, Ж.4.1.3.
Ж.4.1.2. В качестве образцов применяют окрашенные с одной стороны прямоугольные стеклянные пластины размером 100×100 мм. Сторону, подлежащую окрашиванию, промывают горячим раствором бихромата калия в серной кислоте и водой, затем наносят на пластину слой металла толщиной 150 - 200 мкм и шириной 25 - 35 мм. Защищаемый металл наносят термическим методом в вакууме или на пластину наклеивают фольгу металла.
Для контакта с соединительным проводом на края слоя металла наносят слой меди.
К контактам припаивают соединительные провода. Место припайки проводов защищают стойким к данной среде герметиком.
Допускается наносить металл на поверхность стеклянного образца методом, установленным в ГОСТ 9.083, раздел 3.
Ж.4.1.3. Маркировка, измерение толщины покрытия - по ГОСТ 9.083, раздел 3.
Ж.4.2. Требования к средствам испытаний
Требования к средствам испытаний - по Ж.2.2.
Мост в соответствии с требованиями ГОСТ 9.083, раздел 3.
Миллиамперметр М-95.
Ж.4.3. Подготовка к испытаниям
Ж.4.3.1. Подготовка к испытаниям - по Ж.2.3 и Ж.4.3.2.
Ж.4.3.2 Собирают установку для параллельного измерения параметров по схеме, приведенной на рисунке Ж.1.
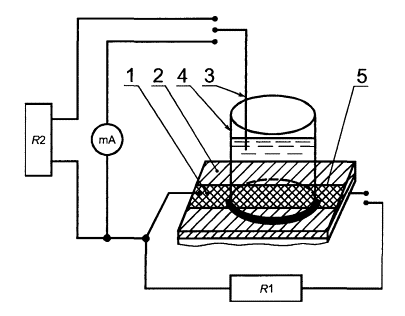
1 - тонкий слой железа; 2 - лакокрасочное покрытие; 3 - платиновый электрод; 4 - стаканчик с подкисленной водой; 5 - пластилин; R1 - мост постоянного тока МО-62; R2 - тераомметр МОИ-4; тА - миллиамперметр М-95
Рисунок Ж. 1 - Схема установки для измерения комплекса параметров-критериев отказа
Ж.4.4. Проведение испытаний
Ж.4.4.1. Испытания образцов - нециклические. На образцы одновременно воздействуют температура, влажность, агрессивный агент.
Ж.4.4.2. При испытаниях периодически в соответствии с требованиями 8.14 измеряют электрическое сопротивление подслоя защищаемого металла, ток гальванической пары «защищаемый металл - медь», электрическое сопротивление покрытия.
Ж.4.5. Обработка результатов
Ж.4.5.1. Относительное уменьшение толщины подслоя металла вычисляют по формуле:
|
Δb/b0 = (R1 - R0)R1, |
(Ж.4) |
где Δb - уменьшение толщины подслоя металла за время испытаний в камере, мкм;
b0 - начальная толщина подслоя металла, мкм;
R1 - электрическое сопротивление подслоя металла после испытаний в камере, Ом;
R0 - электрическое сопротивление металлического подслоя перед испытаниями в камере при температуре испытаний, Ом.
Ж.4.5.2. Строят графики зависимости изменения параметров-критериев отказа от продолжительности испытаний.
Ж.4.5.3. При необходимости проводят параллельное измерение электрического сопротивления покрытия и тока гальванической пары «защищаемый металл - медь».
Измерения проводят на образцах, соответствующих требованиям Ж.2.1.
Ж.5. Определение долговечности электроизоляционных покрытий по изменению уровня электрических параметров покрытия до установленного критического значения (метод 4).
Критерием отказа покрытий электротехнических изделий является пробой покрытия при воздействии испытательного электрического напряжения, для других изделий - параметры по 8.12.
Ж.5.1. Требования к образцам
Ж.5.1.1. Образцами являются окрашенные с обеих сторон металлические пластины размером 100×100 мм.
Ж.5.1.2. Образцы должны соответствовать требованиям Ж.2.1.2 - Ж.2.1.5.
Ж.5.2. Требования к средствам испытаний
Средства испытаний - по Ж.2.2.
Оборудование - в соответствии с требованиями ГОСТ 6433.2, ГОСТ 6433.3, ГОСТ 22372, в зависимости от принятого критерия отказа.
Ж.5.3. Требования к подготовке испытаний - по Ж.2.3.
Ж.5.4. Проведение испытаний
Ж.5.4.1. Испытания образцов - нециклические. На образцы одновременно воздействуют температура, влажность и агрессивный агент.
Ж.5.4.2. При испытаниях периодически в соответствии с требованиями 8.14 образцы извлекают из камеры и выдерживают в течение 2 - 3 ч при нормальных климатических испытаниях по ГОСТ 15150, затем образцы покрытий для электротехнических изделий подвергают испытанию электрическим напряжением, образцы для других изделий - испытанию электрическим напряжением, или измеряют другие требуемые параметры.
Ж.5.4.3. Испытания электрическим напряжением проводят по ГОСТ 6433.3. Образцы выдерживают при испытательном напряжении в течение 1 мин.
Ж.5.4.4. Для определения испытательного напряжения следует провести испытания образцов в одном из наиболее жестких режимов, при этом:
- определяют зависимость пробивного напряжения образцов от логарифма продолжительности испытаний, для чего периодически для части образцов определяют пробивное электрическое напряжение и по полученным данным строят график указанной зависимости;
- определяют пробивное напряжение, при котором данная зависимость стабилизируется (при трех последовательных измерениях через промежутки времени, соответствующие 65 - 100 % общей продолжительности от начала испытаний до предыдущего измерения, уровень пробивного напряжения уменьшается не более чем на 10 % или колеблется в пределах 15 %, и вычисляют среднее значение);
- устанавливают испытательное напряжение на 15 - 20 % выше среднего значения.
Ж.5.4.5. Допускается в качестве испытательного напряжения применять значения, указанные в таблице Ж.1. При этом к образцам прикладывают в течение 1 - 2 с полное испытательное напряжение.
Таблица Ж.1
Выбор испытательного напряжения в зависимости от толщины лакокрасочного покрытия
|
Толщина покрытия, мм |
Испытательное напряжение, В (частота тока 50 Гц) |
Толщина покрытия, мм |
Испытательное напряжение, В (частота тока 50 Гц) |
|
0,040 - 0,050 |
630 |
0,130 - 0,150 |
1170 |
|
0,051 - 0,060 |
680 |
0,160 - 0,180 |
1300 |
|
0,061 - 0,070 |
730 |
0,190 - 0,200 |
1450 |
|
0,071 - 0,080 |
770 |
0,210 - 0,250 |
1750 |
|
0,081 - 0,090 |
850 |
0,260 - 0,300 |
2050 |
|
0,091 - 0,100 |
950 |
0,310 - 0,400 |
3000 |
|
0,110 - 0,120 |
1050 |
0,410 - 0,500 |
4500 |
Ж.5.4.6. Если к электроизоляционному покрытию предъявляют требования выдерживать напряжение больше указанного в Ж.5.4.4 и Ж.5.4.5, испытания проводят при требуемом напряжении.
Ж.5.4.7. Измерение электрических (кроме пробивного напряжения) параметров покрытия, установленных в соответствии с 8.12, проводят по ГОСТ 6433.2, ГОСТ 6433.4, ГОСТ 22372. Метод определения срока L - в соответствии с приложением Б.
Ж.5.5. Обработка результатов
Обработка результатов - по разделу 9 и приложениям А - Д.
Ж.6. Особенности проведения испытаний покрытий образцов деталей и сборочных единиц (далее - деталей)
Ж.6.1. Для определения отсутствия пористости и последующих измерений к зачищенному от края участку металла образца детали припаивают соединительный провод, концы которого очищены от изоляции. Место пайки защищают стойким к испытуемой среде герметикой, затем каждый образец детали помещают в подкисленную (рН 5 - 6) дистиллированную или водопроводную воду и измеряют электрическое сопротивление покрытия тераомметром типа МОМ-4. Тераомметр присоединяют при помощи двух изолированных медных проводов, концы которых зачищены от изоляции и продуктов коррозии. Концы одного провода спускают в воду, концы другого - подсоединяют к соединительным проводам образца детали. Сопротивление измеряют через 2, 15, 60 мин и 24 ч.
Покрытие считают беспористым, если его начальное электрическое сопротивление более 107/Sg Ом и наибольшее уменьшение в течение 24 ч составляет:
для начального сопротивления св. 107/Sg до l08/Sg -103 Ом;
» » » » 108/Sg до 1010/Sg - 104 Ом;
» » » » 1010/ Sg до 1014/Sg - 105 Ом,
где Sg - площадь покрытия образца детали, см2, округленная до 10.
Ж.6.2. При испытаниях покрытий образцов деталей по методу 1 электрическое сопротивление покрытия измеряют по Ж.6.1, при этом проводят только одно измерение по истечении 2 мин после погружения образца в воду.
Критическим критерием отказа является значение электрического сопротивления покрытия в предельном состоянии (электрическое сопротивление разрушения) Rкр. Для его определения проводят испытания по Ж.2.4.2 в одном из наиболее жестких режимов до отказа всех образцов деталей и находят зависимость электрического сопротивления каждого образца детали от продолжительности испытаний. Затем определяют электрическое сопротивление разрушения покрытия Rкр по ГОСТ 9.083, раздел 4, но не вычисляют приведенное сопротивление разрушения Rпр.кр, и строят график в координатах R - t.
Ж.6.3. При испытании по методу 4 образцы деталей помещают в воду в соответствии с требованиями Ж.6.1. По истечении 2 мин между соединительным проводом образца детали и погруженным в воду другим соединительным проводом прикладывают испытательное напряжение.
Ж.6.4. Допускается (например, для крупногабаритных и (или) дорогостоящих деталей и сборочных единиц) проводить испытания по варианту 6 приложения А.
Ж.6.5. Расчет показателей долговечности покрытий в смесях некоторых газообразных сред по результатам испытаний в каждой среде.
Срок L покрытия в смеси органических кислот или их паров Lcм вычисляют по формуле:
1/Lсм = 1/L1 + 1/L2 + 1/L3+……,
где L1, L2, L3 - соответственно сроки L покрытия в каждом из компонентов смеси.
Допускается применять эту формулу для покрытий в смеси других агрессивных сред, если предварительными исследованиями установлено, что механизм отказа конкретного покрытия в этих средах одинаков.
ПРИЛОЖЕНИЕ
З
(обязательное)
Методы расчета показателей долговечности покрытий в смесях некоторых сред по
результатам испытаний в каждой из сред
Срок L покрытия в смеси Lcм для органических кислот или их паров может быть рассчитан по формуле:
|
1/Lсм = 1/L1 + 1/L2 + 1/L3+…., |
(З.1) |
где L1, L2, L3…. - соответственно сроки L покрытия в каждом из компонентов смеси.
Допускается применение этой формулы для покрытий в смеси других агрессивных сред, если предварительными исследованиями установлено, что механизм отказа конкретного покрытия в этих средах одинаков.
ПРИЛОЖЕНИЕ
И
(справочное)
Протокол испытаний
Протокол испытаний должен содержать:
1) описание испытательных образцов;
2) описание условий испытаний (основные воздействующие факторы, дополнительные факторы, имитирующие эксплуатационные, критерии отказа и т.п.);
3) результаты испытаний;
4) аналитическую зависимость срока L от основных воздействующих факторов (указывают формулу с числовыми коэффициентами);
5) уравнение нижнего доверительного предела среднего срока с доверительной вероятностью ….. % (указывают формулу);
6) уравнение нижнего толерантного предела при вероятности безотказного хранения (работы) ….. % с доверительной вероятностью ….. % (приводят уравнение);
7) нижние граничные значения допустимых пределов экстраполяции:
а) по значению концентрации коррозионно-активного агента,
б) по значению относительной влажности воздуха,
в) по значению температуры;
8) сроки L, полученные расчетом при рабочих значениях воздействующих факторов, а при их отсутствии - при граничных значениях допустимых пределов экстраполяции, среднее значение, нижнее доверительное значение по перечислению 5), нижний толерантный предел по перечислению 6).
ПРИЛОЖЕНИЕ
К
(справочное)
Перечень обозначений математических символов
В таблице К.1 (графы «Где определяется» и «Где встречается») буквами и цифрами обозначены номера формул или пунктов (в последнем случае перед номером стоит буква «п.»). Если формула применена в таблице, то после номера формулы указана буква «т.».
Таблица К.1
Перечень обозначений математических символов
|
Обозначение символа |
Где определяется |
Где встречается |
|
L |
п. 4.2 |
По всему стандарту |
|
Li |
А.5в |
Б.1а, Б.1б |
|
|
А.5в |
Приложение А |
|
|
п. А.2.9.3 |
То же |
|
|
А.5в |
» |
|
C |
2 |
По всему стандарту и приложениям |
|
η |
2 |
То же |
|
T |
2 |
» |
|
Куск |
3 |
» |
|
Тэ |
п. В.2 |
» |
|
Сэ |
п. В.2 |
» |
|
ηэ |
п. В.2 |
» |
|
Тэ |
п. В.2 |
» |
|
Сн |
п. В.2 |
» |
|
ηн |
п. В.2 |
» |
|
Тн |
1 |
1 |
|
A |
2 |
2; А.1 |
|
A' |
2 |
1; В.1; В.3; В.4; В.6 |
|
B |
2 |
2; А.1; В.3 |
|
B' |
2 |
2; А.1; В.6 |
|
m |
2 |
2; А.1; В.4 |
|
a1 |
А.1 |
А.1; А.16; п. Б.6.5.1 |
|
a2 |
А.1 |
А.1; А.16; п. А.3.2; п. А.3.3; п. Б.5; В.2; В.3; В.5; В.7 |
|
a3 |
А.1 |
А.1; А.13; п. А.3.1; п. А.3.2, п. А.3.5; п. Б.5; В.5; В.7; Е.13т. |
|
a4 |
А.1 |
А.1; А.14; п. А.3.1; п. А.3.2; п. А.3.5; п. Б.5; В.5; В.7; Е.14т. |
|
a1k |
А.23 |
п.А.1; п.А.3.3; А.23; А.41 |
|
a2k |
А.23 |
п. А.3.3; п. А.3.4; А.23 - А.25; А.31; А.35; А.41; Е.21т.; Е.22т. |
|
|
А.24 |
п. А.3.5; А.24; А.25; Е.22т. |
|
a3k1 |
А.30 |
А.30 |
|
|
А.30 |
А.30 |
|
axk |
А.31 |
А.31; А.35; А.36 |
|
ax1 |
А.34 |
А. 34 |
|
a21 |
А.33 |
А.33; А.34; Е.17т |
|
Б |
Е.3 |
Е.3 |
|
Б1 |
Е.4 |
Е.З, Е.4 |
|
b1 |
Б.1; Б.1а |
Б.1; Б.1а; п. Б.3б; Б.6; п. Б.7.7; Б.10 - Б.14 |
|
b2 |
п.4.3; Б.1 |
По всему стандарту и приложениям |
|
b2i |
Б.1в |
Б.1а - Б.1в |
|
|
Б.13 |
Б.1а; Б.1б; Б.12; Б.13 |
|
b2P* |
п. Б.8.3 |
п. Б.8.3; Б.17 |
|
|
Б.20 |
Б.19; Б.20 |
|
b |
А.4; А.4а |
А.3; А.4; А.4а; А.7; А.19; А.20; А.42; А.43; п. Б.6.5.3; Б.1г; Е.25т. |
|
bcep1 |
А.38 |
А.37; А.38; А.40; Е.23т; Е.24т |
|
bcepk |
А.40 |
А.39; А.40; Е.24т |
|
bд |
В.8 |
В.8 |
|
b2тp |
Б.6.5.2 |
Б.1з; п. Б.6.5.2; п. Б.6.5.4 - п. Б.6.5.6 |
|
b2P*.тр |
Б.1ж |
Б.1ж; Б.1и |
|
b2P.тр |
Б.1ж |
Б.1ж; Б.1к |
|
D |
п. Е.1.2 |
п. Е.1.2; Е.9т - Е.17т |
|
Еэфф |
В.3 |
В.3 |
|
П |
Б.1 |
Б.1 |
|
Пкр |
п. Б.6.2 |
Б.1а; Б.1б |
|
f(П) |
п. Б.6.5.8 |
п. Б.6.5.8 |
|
|
Б.1 |
Б.1; п. Б.3б; п. Б.8.1 |
|
f(П)изм |
Б.2 |
Б.2; п. Б.8.1 |
|
f(П)изм |
Б.2 |
Б.2; Б.3; Б.7; Б.15 |
|
f(П)изм |
Б.3 |
Б.3 - Б.5; Б.7; Б.8 |
|
f(П)реж |
Б.15 |
Б.8 - Б.15 |
|
f(П)тр |
Б.4 |
Б.4 - Б.6 |
|
f(П)Р*тр |
Б.1з |
Б.1з; п. Б.6.5.8 |
|
f(П)Р.тр |
Б.1и |
Б.1и |
|
f1 |
Б.1к |
Б.1к |
|
f2 |
А.25 |
А.25; А.29 |
|
fs |
А.28 |
А.28; А.29 |
|
fst |
А.2 |
А.2; А.17 |
|
fs1 |
А.5; А.38 |
А.5;А.38 |
|
f4k |
А.6 |
А.6 |
|
f3k |
Д.4 |
Д.1; Д.4; Е.3; Е.4 |
|
fi |
Д.6 |
Д6 |
|
fБ |
Д.1 |
Д.1; Е.3; Е.4 |
|
f |
Е.5 |
Е.5 |
|
i |
А.4 |
По приложениям А - Д |
|
k |
А.23; Б.22 |
А.17; А.18; А.23 - А.25; А.28; Б.22; Б.23; Д.8; Е.21т.; Е.22т. |
|
k1 |
А.30 |
А.30 |
|
kи |
п. В.2 |
В.1; В.2; В.4 - В.7 |
|
m1 |
А.15; Б.18; Е.20т. |
А.2; А.15; А.18; Е.20т.; Е.25т.; Б.18; Б.20 - Б.23; |
|
N |
А.4 |
п. А.2.5; А.4; А.6; А.7; А.8; А.17; А.18; А.20; п. А.3.3; А.43; Б.1е; Е.20т.; Е.25т. |
|
n'изм |
Б.2 |
Б.2 |
|
nизм |
Б.3 |
Б.3; Б.7; Б.8; Б.15; Б.16 |
|
nреж |
Б.4 |
Б.4; Б.5; Б.7; Б.8; Б.11 - Б.13; Б.15; Б.16 |
|
ni |
А.4; Б.15 |
А.2; А.4; А.4а; А.18; А.20; А.26; А.27; А.38; А.40; Б.10; Б.15; Б.16; Б.21; Б.22; Д.2; Д.5; Е.7т; Е.8т.; Е.10т.; Е.12т. - Е.14т.; Е.16т. - Е.21т.; Е.23т.; Е.24т. |
|
nxi |
А.4 |
А.4; А.4а; А.9; А.10; А.20; А.25 - А.27; А.32; А.38; А.40; Д.1; Д.4 - Д.6; Е.3 - Е.5; Е.6т. - Е.8т.; Е.15т.; Е.19т.; Е.22т - Е.24т. |
|
nyi |
А.4 |
А.4; А.4а; А.11; А.13; А.20; Д.2; Е.9т.; Е.10т.; Е.13т.; Е.20т. |
|
nzi |
А.4 |
А.4; А.4а; А.12; А.14; А.20; Д.2; Е.11т.; Е.12т.; Е.14т.; Е.20т. |
|
ncep |
А.26 |
А.26; А.27; Е.19т.; Е.22т. |
|
nik |
п. А.3.3 |
п. А.3.3 |
|
ncep1 |
А.37 |
А.37; А.38; А.40; Е.23т.; Е.24т. |
|
ncep.k |
А.40 |
А.39; А.40; Е.24т. |
|
nk |
А.43 |
А.43; Е.25т. |
|
nic |
Г.1 |
Г.1; Г.2 |
|
nц |
Д.3 |
Д.3 |
|
nxik |
Е.24т. |
Е.24т. |
|
P* |
п. А.2.6; п. Б.8.3 |
п. А.2.6; А.6; Б.17; п. Б.6.5.4; п. Б.6.5.5; Е.5 |
|
P |
п. Б.6.5.5 |
п.А2.6; п. Б.6.5.5 |
|
R |
В.3 |
В.3 |
|
S2 |
А.2 |
А.2; А.3; А.6 - А.8; А.18; п. А.3.2; А.25; п. А.3.4; Б.24; Д.8 |
|
|
Б.7 |
Б.7; Б.9 |
|
|
Б.8 |
Б.8; Б.9 |
|
|
Б.10 |
Б.10; Б.11 |
|
|
Б.11 |
Б.11; Б.14 |
|
|
Б.12 |
Б.12; Б.14 |
|
|
Б.15 |
Б.10; Б.15; Б.16 |
|
|
Б.16 |
Б.16 - Б.18; Б.1в |
|
|
Б.18 |
Б.18; Б.19 |
|
|
Б.19 |
Б.19; Б.24 |
|
|
Б.22 |
Б.22; Б.24; Д.5; Д.7; Д.8 |
|
|
Б.24 |
Б.24 |
|
|
п. Б.6.3 |
Б.1в |
|
|
п. А.2.5 |
п. А.2.5; А.5; А.19; п. А.3.2; п. А.3.3; А.37; А.39; А.42; п. Б.6.5.3; п. Б.9д |
|
|
Б.1г |
Б.1г; Б.1е |
|
|
А.19 |
п. А3.2; п. А.3.3 |
|
|
А.25 |
А.25; А.29 |
|
|
А. 26; А.27 |
А.26 - А.28; п. А.3.4; А.37; А.39; Е.2 |
|
|
А.28 |
А.28; А.29; А.42; Е.2 |
|
|
А.37 |
А.37 |
|
|
А.39 |
А.39; А.42 |
|
|
В.8 |
В.8; В.9 |
|
|
В.8 |
В.8; В.9 |
|
|
В.8 |
В.8; В.9 |
|
|
В.9 |
В.9 |
|
|
В.9 |
В.9 |
|
|
В.9 |
В.9 |
|
|
Г.2 |
Г.2; Г.3; Д.4 |
|
|
Д.2; Д.3 |
Б.1в; п. Б.6.4; Д.1 - Д.4; Е.1; Е.3 |
|
|
Д.1 |
Д.1; Д.4; Д.7; Д.8; Е.1; Е.3 |
|
U |
А.1 |
А.1; п. А.1; п. Б.6.5.1 |
|
|
п. Б.6.5.2 |
Б.1д; п. Б.6.5.1 |
|
UbP* |
Б.1д |
Б.1д - Б.1ж |
|
UbP |
Б.1е |
Б.1е; Б.1ж |
|
Uи |
п. А.2.3 |
п. А.2.3 |
|
|
А.5 |
п. А.2.3; А.5; А.7; А.8 |
|
UP |
А.5 |
А.5; А.6 |
|
Uзад |
А.6 |
А.6; А.7 |
|
|
А.8 |
А.8 |
|
|
А.9 |
А.9; А.10; А.27; А.32; А.33; Е.6т.; Е.15т.; Е.17т. |
|
|
А.9 |
А.9; А.10; А.32; А.35; А.41; Е.6т.; Е.8т. |
|
|
А.32 |
А.32-А.34; Е.17т. |
|
|
А.11 |
п. А.3.2; А.11; А.13; Е.9т.; Е.13т. |
|
|
А.11 |
А.11; А.13; Е.9т.; Е.13т. |
|
|
А. 12 |
А.12; А. 14; п. А.3.2; Е.11т.; Е.14т: |
|
|
А.12 |
А.12; А.14; Е.11т.; Е.14т. |
|
|
А.15 |
А.15; А.16; А.30 |
|
|
А.31 |
А.31 |
|
|
А.2 |
А.2; А.18; А.25; Б.16; Г.1; Г.2; Д.2 |
|
|
А.15; Б.22 |
А.15; п. Б.6.2; п. Б.6.4; Б.22; Д.2; Д.5; Е.18т. |
|
|
Г.1 |
Г.1; Г.2 |
|
|
А.2; Б.22 |
А.2; А.18; А.25; Б.16; Б.22; Д.5 |
|
|
А.21 |
А.21 |
|
|
А.21 |
А.21 |
|
|
А.22 |
А.22 |
|
|
А.22 |
А.22 |
|
|
А.23 |
А.23 |
|
|
А.26 |
А.26; Е.19т. |
|
|
А.26 |
А.26; А.27; Е.19т. |
|
|
А.36 |
А.36 |
|
|
А.36 |
А.36 |
|
|
Г.3 |
Г.3 |
|
|
Г.3 |
Г.3 |
|
ΔU |
Д.3 |
Д.3 |
|
|
А.27 |
А.27 |
|
хэ |
3 |
3; А.4а; В.2; В.5; В.7 |
|
уэ |
3 |
3; А.4а; В.7 |
|
zэ |
3 |
3; А.4а; В.5 |
|
хи |
3 |
3; А.4а |
|
уи |
3 |
3; А.4а |
|
zи |
3 |
3;А.4а |
|
хтр |
А.4 |
А.4; А.20; А.38; А.40; А.43; В.2; Е.23т.; Е.25т. |
|
утр |
А.4 |
А.4; А.20; В.5; В.7 |
|
zтр |
А.4 |
А.4; А.20 |
|
|
А.4 |
А.4; А.4а; А.9; А.10; А.20; А.25; А.32; А.38; А.40; А.43; Е.8т.; Е.20т.; Е.22т.; Е.23т.; Е.25т. |
|
|
А.4 |
А.4; А.4а; А.11; А.13; А.20; Е.10т.; Е.13т. |
|
|
А.4 |
А.4; А.4а; А.12; А.14; А.20; Е12т.; Е.14т. |
|
|
А.9 |
А.9; А.10; А.25; А.32; А.41; Е.7т.; Е.8т.; Е.22т. |
|
|
А.11 |
А.11; А.13; Е.10т.; Е.13т. |
|
|
А.12 |
А.12; А.14; Е.12т.; Е.14т. |
|
xi |
А.15 |
А.15 |
|
yi |
А. 15 |
А.15 |
|
zi |
А.15 |
А.15 |
|
|
А.15 |
А.4; А.4а; А.15; А.16; А.20; А.30; А.38; А.40; А.43; Е.23т. - Е.25т. |
|
|
А.15 |
А.4; А.4а; А.15; А.16; А.20; А.30 |
|
|
А.15 |
А.4; А.4а; А.15; А.16; А.20; А.30 |
|
|
А.21 |
А.21; А.22 |
|
|
А.21 |
А.21 |
|
|
А.22 |
А.22 |
|
|
А.32 |
А.32; А.33; Е. 16т.; Е. 17т. |
|
|
А.32 |
А.32 - А.34; Е.16т.; Е.17т. |
|
xn |
п. В.2 |
В.2; В.5; В.7; В.8 |
|
yn |
п. В.2 |
В.8 |
|
zn |
п. В.2 |
В.8 |
|
Un |
А.6 |
А.6 - А.8; Б.1е |
|
zp |
А.6 |
А.6 - А.8; Б.1е; Д.3 |
|
t |
А.5 |
А.5; А.7; А.8; Б.1д; Б.17 |
|
χ2 |
А.6 |
А.6; п. Е.2.2 |
|
λkc |
Г.3 |
Г.3; п. Г.7 |
|
τ |
п. Б.1 |
п. 8.17.2г; п. Б.1; Б.1з - Б.1к |
|
τлин |
п. Б.3в |
п. Б.3в; рисунок Б.2 |
|
|
Б.4 |
Б,4; Б.5; Б.16 |
|
|
Б.4 |
Б.4 - Б.6; Б.16 |
|
τи |
п. 9.4г |
4 |
|
τэ |
п. 9.4г |
4 |
|
ωik |
Е.1 |
Е.1; Е.6т. - Е.22т.; Е.24т.; Е.25т. |
|
ωi1 |
Е.23т. |
Е.23т. |
|
ωk |
Е.2 |
Е.2; Е.21т.; Е.22т. |
|
ωix |
п. Е.1.6 |
Е.20т. Е.25т. |
|
ωiy |
п. Е.1.6 |
Е.20т.; Е.25т. |
|
ωiz |
п. Е.1.6 |
Е.20т.; Е.25т. |
ПРИЛОЖЕНИЕ
Л
(справочное)
Л.1 Сравнение показателей настоящего стандарта с показателями международных
стандартов МЭК и ИСО.
Сравнение показателей приведено в таблице Л.1
Таблица Л.1
Сравнение показателей настоящего стандарта с показателями международных стандартов
|
Наименование показателя |
Настоящий стандарт |
МЭК 60068-2-43-79, МЭК 60068-2-46-83 |
МЭК 60068-2-42-82, МЭК 60068-2-49-83 |
ИСО 10062-91 |
|
1 Цель испытаний |
Ускоренные испытания на долговечность и сохраняемость при совместном или раздельном воздействии температуры, влажности и агрессивной среды, включающие определение сроков L при заданном воздействии или величины допустимых воздействий при заданных сроках L |
Сравнительные испытания для ускоренного определения коррозионного воздействия атмосферы, содержащей сероводород (H2S), на контакты, выполненные из серебра и его сплавов; серебра, защищенного другим слоем; других металлов, покрытых серебром или его сплавами |
Сравнительные испытания для ускоренного определения только коррозионного воздействия атмосферы двуокиси серы (S02) на контактные соединения; не применимы для получения данных о сроке службы |
Сравнительные испытания качества изготовления материалов и защитных покрытий при воздействии атмосферы, содержащей двуокись серы (S02), сероводород (H2S), смеси двуокиси серы и сероводорода, смеси сероводорода, двуокиси серы и хлора (Cl)/He применимы для получения данных о сроке службы |
|
2 Объект испытаний |
Изделия, полимерные материалы, металлы и сплавы, детали и узлы из них; конструкции электрической изоляции и защитные покрытия от коррозии |
Контакты из серебра и его сплавов; серебра, защищенного другим слоем; других металлов, покрытых серебром или его сплавами |
Контакты из благородных металлов или покрытий благородными металлами, за исключением контактов из серебра для изделий электронной техники |
Контакты и контактные соединения из серебра и его сплавов без защитного покрытия или с защитными покрытиями, а также для контактов и контактных соединений из других металлов с защитными покрытиями из серебра и его сплавов |
|
3 Требования к аппаратуре |
+ |
- |
- |
- |
|
4 Требования к проведению испытаний: 4.1 Общие требования к режиму испытаний в агрессивных средах |
+ |
+ |
+ |
+ |
|
4.2 Выбор температурно-влажностного выявляющего режима и продолжительность цикла: |
|
|
|
|
|
4.2.1 Общие требования |
+ |
- |
- |
- |
|
4.2.2 Наличие и величины конкретных значений |
+ |
- |
- |
- |
|
4.2.3 Испытания греющихся и негреющихся изделий |
+ |
- |
- |
- |
|
5 Методы обработки результатов: |
|
|
|
|
|
5.1 Обработка экспериментальных данных на базе логарифмически нормального закона распределения отказов |
+ |
- |
- |
- |
|
5.2 Метод определения коэффициента ускорения испытаний и срока L сравнением скоростей изменения значений параметров-критериев отказа |
+ |
- |
- |
- |
|
5.3 Метод исключения резко выделяющихся значений результатов испытаний |
+ |
- |
- |
- |
|
5.4 Обработка экспериментальных данных при неравноточных измерениях |
+ |
- |
- |
- |
|
5.5 Метод статистической обработки результатов при параллельных испытаниях деталей и стандартных образцов из тех же материалов |
+ |
- |
- |
- |
|
5.6 Определение показателей при переменных значениях воздействующих факторов |
+ |
- |
- |
- |
|
5.7 Методы обработки на базе закона распределения отказов Вейбулла |
+ |
- |
- |
- |
|
5.8 Методы обработки на базе закона нормального распределения отказов |
+ |
- |
- |
- |
|
5.9 Связь с показателями надежности изделии |
+ |
- |
- |
- |
|
5.10 Метод установления режимов контрольных испытании |
|
|
|
|
|
5.10.1 Требования по выбору режимов испытаний для подтверждения или определения ресурсов, сроков службы и сохраняемости |
+ |
- |
- |
- |
|
5.10.2 Режимы сравнительных испытаний, не предназначенные для определения ресурсов, сроков службы и сохраняемости. Требования к конкретным значениям параметров испытательного режима |
|
|
|
|
|
5.10.2.1 Температура, °С |
|
|
|
|
|
5.10.2.2 Относительная влажность, % |
|
|
|
|
|
5.10.2.3 Вид и концентрация агрессивного агента, мг/м3 [объемная концентрация] |
Общие требования по выбору значений |
340-410 мг/м3 [(10-15)·10-6 |
70 мг/м3 (25·10-6) |
Метод A: SО2. 1,4 мг/м3 (0,5·10-6). Метод В: H2S. 3,4 мг/м3 (10·10-6) |
Л.2. Ограничения при выборе диапазонов значений воздействий при ускоренных испытаниях электрических контактов на долговечность и сохраняемость в агрессивных средах H2S и SО2
Л.2.1. Испытания электрических контактов в SО2
Л.2.1.1. При значениях относительной влажности 80 - 85 % возможно изменение состава продуктов коррозии.
Л.2.1.2. При температурах 30 - 35°С возможны изменения механизмов возникновения отказа, поэтому возможность использования более высоких испытательных температур должна быть проверена способами, указанными в 6.3, 8.7 и 8.8.
Л.2.2. Испытание серебряных или серебросодержащих контактов в H2S
Л.2.2.1. При значении относительной влажности св. 85 % возможно изменение состава продуктов коррозии.
Л.2.2.2. При температурах св. 30 - 35°С возможны изменения механизмов возникновения отказа, поэтому возможность использования более высоких температур должна быть проверена способами, указанными в 6.3, 8.7 и 8.8.
Л.2.2.3. При концентрации св. 410 мг/м3 (15·10-6), что соответствует превышению над концентрацией в природе примерно в 5000 раз, возможно начало изменения состава пленок продукта коррозии по сравнению с образующимся в природе. Изменения концентрации примерно в 1000 раз увеличивает скорость коррозии контактов примерно в 10 раз.
Примечания
1. Рекомендации настоящего раздела используют при ускоренных испытаниях по методам настоящего стандарта с экстраполяцией результатов в область эффективных значений внешних воздействующих факторов.
2. Рекомендации составлены с учетом данных МЭК 60068-2-46-82 и МЭК 60068-2-49-83, хотя последние не предусматривают экстраполяции результатов.
3. Рекомендации настоящего раздела в части относительной влажности и концентрации агрессивной среды относятся только к открытым контактам, эксплуатирующимся в условиях категории 1 по ГОСТ 15150.
|
Ключевые слова: агрессивные среды, специальные среды, методы ускоренных испытаний, долговечность, сохраняемость, технические изделия, системы материалов, материалы, форсирование воздействий температуры, влажности, концентрации агрессивной среды |
| Расположен в: |
|---|
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/37953
На эту страницу сайта можно сделать ссылку:
На правах рекламы:
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|