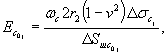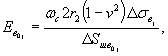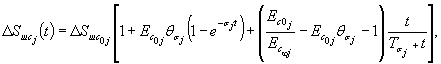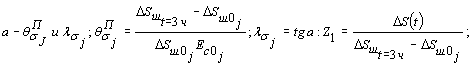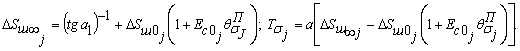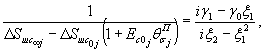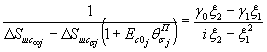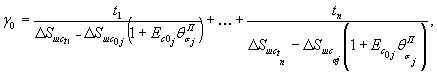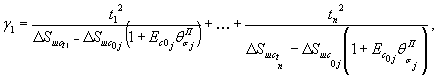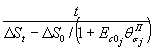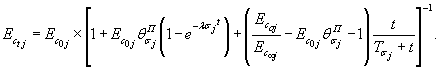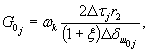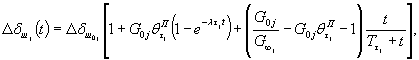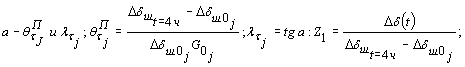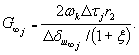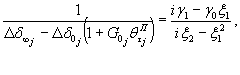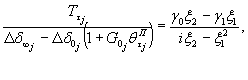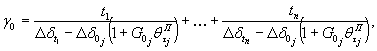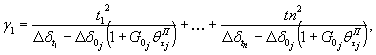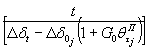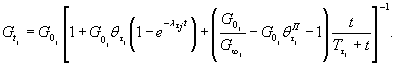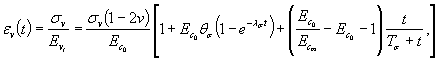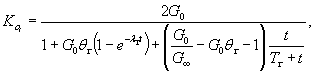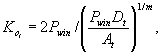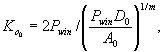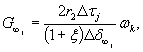
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"43-89 Рекомендации по определению характеристик реологических свойств скальных и полускальных грунтов методом кольцевого нагружения (мерзлых, оттаявших и немерзлых).МИНИСТЕРСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ СССР ВСЕСОЮЗНЫЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ РЕКОМЕНДАЦИИ ПО ОПРЕДЕЛЕНИЮ П-43-89 ВНИИГ ЛЕНИНГРАД 1990 Дана методика определения реологических свойств мерзлых и талых скальных и полускальных пород, необходимых для расчетов и моделирования системы «подземное сооружение - горный массив», выбора и обоснования конструктивных особенностей и технологии возведения сооружений. Исходя из пространственного характера напряженного состояния массива, предлагается для определения реологических характеристик метод кольцевого нагружения монолита или массива грунта. Даны научное обоснование метода, конструкции установок, технология ведения экспериментов, результаты обработки материалов испытаний. Распространение характеристик реологических свойств на отдельные элементы массива горных пород выполняется на основе инженерно-геокриологического моделирования, учитывающего структурно-геологические особенности пород, их криогенное строение и температурный режим. Особо важная роль отводится геофизическим методам исследований. Рекомендации предназначены для научных работников, проектировщиков, строителей, занимающихся обоснованием, проектированием и возведением подземных гидротехнических сооружений. СодержаниеПРЕДИСЛОВИЕВажнейшими расчетными параметрами, определяющими тип конструкции, размеры и технологию возведения крепей и обделок подземных гидротехнических сооружений, строящихся в мерзлых массивах, являются характеристики деформируемости и прочности скальных и полускальных грунтов в мерзлом состоянии и после их оттаивания. Как известно, мерзлые, оттаявшие и немерзлые скальные и полускальные грунты обладают явно выраженными реологическими свойствами - ползучестью, релаксацией напряжений, изменением прочности во времени, причем при оттаивании они могут резко менять свои механические свойства [7, 12, 13, 18, 39, 51, 52]. Определение характеристик реологических свойств необходимо для решения основных вопросов проектирования и строительства подземных гидротехнических объектов, в частности: - для расчетов напряженно-деформированного состояния системы подземное сооружение - горный массив, включая вопросы оценки прочности и устойчивости массива вокруг незакреплённых горных выработок с целью разработки рекомендаций по конструкции и технологии временного и постоянного креплений; - для определения типа конструкций и размеров обделок напорных туннелей и шахт; - для моделирования, в том числе и численного, совместной работы сооружений и массива в сложных инженерно-геологических условиях [27, 30, 50]; - при разработке технологии строительства подземных сооружений, включая вопросы их поэтапного возведения; - для анализа данных натурных наблюдений в процессе строительства и эксплуатации подземного сооружения с целью уточнения прогнозов их работоспособности. В соответствии с требованиями СНиП 2.06.09-84 «Туннели гидротехнические» характеристики механических свойств грунтов для обоснования проектов подземных гидротехнических сооружений следует определять на характерных инженерно-геологических участках по данным натурных исследований. Учитывая пространственный характер напряженного состояния массива при его совместной работе с подземными конструкциями, метод испытания должен позволять устанавливать закономерности деформирования и прочности грунтов для условий сложного напряженного состояния, в частности, с учетом влияния всестороннего давления. Это даст возможность более полно использовать современные методы расчета совместной работы конструкций и массива, в том числе и на основе использования численных методов [5, 8, 15, 50], тем самым приблизив результаты расчетных прогнозов к реальному взаимодействию массива и конструкции. Такие данные о механических свойствах мерзлых, оттаявших и немерзлых грунтов с точностью, достаточной для практических целей и для решения широкого круга задач, могут быть получены из результатов натурных, а в ряде случаев н лабораторных испытаний методом кольцевого нагружения (МКН). Метод кольцевого нагружения предложен и разработан в ОНИЛИМЭС [1 - 4, 21, 5] и основан на приложении к массиву или монолиту грунта (в том случае, если опыты выполняются в лабораторных условиях) кольцевой нормальной, растягивающей или сжимающей и касательной нагрузок. В частном случае, на основе испытаний МКН определяются параметры деформируемости и прочности скальных и полускальных грунтов в массиве для стабилизированного состояния, используемые в традиционных методах расчета: модуль деформации Е, коэффициент Пуассона v, коэффициент удельного отпора K0, параметры пиковой и остаточной прочности сопротивления сдвигу φ и С, и прочности σпр на одноосное сжатие и растяжение. Рекомендации базируются на материалах исследований и изысканий, выполненных ОНИЛИМЭС при МИСИ им. В.В. Куйбышева за период 1976-1987 гг. В них также учтен отечественный и зарубежный опыт геомеханических исследований в этой области техники [9 - 11, 16, 18, 19, 31, 32, 34, 38, 42 - 44, 48, 49]. Большое содействие в организации этих исследований оказали Н.А. Цытович, С.Б. Ухов, В.М. Мостков, С.С. Вялов, Я.А. Кроник, Н.Ф. Кривоногова, О.С. Мазуров, В.Н. Бурлаков. Рекомендации разработаны и составлены ОНИЛИМЭС при МИСИ им. В.В. Куйбышева (канд. техн. наук, доц. В.Л. Кубецкий) при участии отдела грунтовых плотин и оснований ВНИИГ им. Б.Е. Веденеева (канд. геол.-мин. наук. Н.Ф. Кривоногова - лаборатория инженерной геологии и геокриологии и канд. техн. наук Д.Д. Сапегин - лаборатория скальных оснований и подземных сооружений). Научное редактирование выполнено доктором техн. наук, профессором С.С. Вяловым. В исследованиях отдельных вопросов по теоретическому и экспериментальному обоснованию МКН принимали участие аспиранты кафедры механики грунтов, оснований и фундаментов МИСИ Т.Т. Ахмад, В.А. Козионов, М.В. Королев, А.Б. Лолаев и сотрудники ОНИЛИМЭС канд. геол-мин. наук Н.С. Беспалова, мл. н. сотр. В.П. Колотухин, канд. техн. Наук B.Н. Шрамкова. В ходе подготовки Рекомендаций к изданию большую помощь оказала инженер В.Ю. Матвеева. При составлении Рекомендаций были учтены замечания и предложения ряда организаций: института Гидропроект им. C.Я. Жука и его филиалов, НИИ оснований и подземных сооружений им. Н.М. Герсеванова, ВНИМИ, ПНИИИС, ВСЕГИНГЕО, ЛГТУ, ЛИСИ, а также специалистов ВНИИГ и кафедры МГрО и Ф МИСИ им. В.В. Куйбышева. При подготовке данной редакции Рекомендаций использованы советы и замечания А.К. Бугрова, О.К. Воронкова, С.Е. Гречишева, Б.Д. Зеленского, Ю.М. Карташова, В.М. Мосткова, М.В. Малышева, А.И. Савича, 3.Г. Тер-Мартиросяна, Е.М. Шафаренко, Р.А. Ширяева, Ю.А. Фишмана. Рекомендации являются первым нормативно-методическим документом, касающимся вопросов исследования реологических свойств скальных и полускальных грунтов статическим методом применительно к обоснованию проектов подземных гидротехнических объектов в Северной строительно-климатической зоне. В связи с этим не все вопросы в Рекомендациях получили одинаковое освещение. В будущем предполагается обобщить опыт использования описанной методики и учесть его в последующих изданиях Рекомендаций. Замечания и пожелания просьба направлять в адрес ВНИИГ им. Б.Е. Веденеева: 195220, Ленинград, Гжатская ул., д.21. Отдел грунтовых плотин и оснований. Рабочие чертежи полевой установки и лабораторных стендов можно получить по адресу: 129336, Москва, Ярославское шоссе, д. 26, МИСИ им. В.В. Куйбышева, ОНИЛИМЭС.
1. ОБЩИЕ ПОЛОЖЕНИЯ1.1. Рекомендации необходимо использовать при геомеханических исследованиях скальных и полускальных массивов для целей строительства подземных гидротехнических сооружений, возводимых в области распространения многолетней мерзлоты. Примечания: 1. При пользовании положениями настоящих Рекомендаций следует также соблюдать требования СНиП на проектирование подземных сооружений (2.06.09-84), оснований сооружений (2.02.01-83, 2.02.02.85) и других общесоюзных и ведомственных нормативно-методических документов, относящихся к вопросу определения механических свойств скальных и полускальных грунтов оснований сооружений и массивов. 2. Основные положения Рекомендаций могут быть использованы для определения реологических свойств скальных и полускальных грунтов вне ССКЗ. 3. Рекомендации не распространяются на определение реологических свойств скальных и полускальных грунтов в процессе их оттаивания. 4. Отнесение грунта к скальному или полускальному выполняется в соответствии с классификацией СНиП 2.02.02-85, а для грунтов, находящихся в мерзлом состоянии, после их оттаивания. 5. В Рекомендациях изложены требования по подготовке и проведению исследований реологических свойств квазиоднородных массивов. При необходимости определения свойств неоднородных массивов этот вопрос решается для условий конкретной строительной площадки на основе составления геомеханической модели исследуемого массива с использованием сейсмических и других методов, исходя из принципиальных положений, данных в работах [33, 36, 37, 40, 49]. 1.2. Рекомендации распространяются на полевые и лабораторные статические испытания, выполняемые методом кольцевого нагружения, для определения реологических свойств мерзлых, оттаявших и немерзлых скальных и полускальных грунтов, вмещающих подземные гидротехнические сооружения всех классов капитальности.
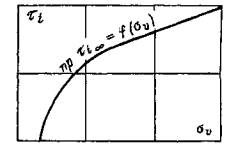
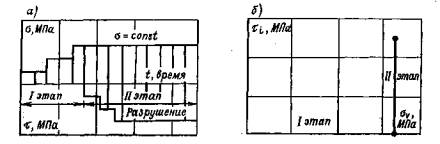
1.3. Строительство и эксплуатация подземных гидротехнических сооружений приводит к изменению температурного режима, вмещающего сооружение массива, и в результате к его оттаиванию. В связи с этим реологические свойства грунтов следует определять в мерзлом и оттаявшем состоянии [17]. 1.4. На первых стадиях проектирования реологические свойства указанных грунтов в мерзлом состоянии и после их оттаивания допускается определять в лабораторных условиях по результатам испытания монолитов, отобранных на характерных участках, с сохранением их естественного состояния. 1.5. При наличии определенно выраженных трещин и ослабленных плоскостей в массиве, а также тектонических зон, параметры их сопротивления сдвигу и деформируемость заполнителя трещин надлежит определять по специальным методикам [36, 43]. 1.6. Исследования реологических свойств грунтов необходимо проводить на основе технической и рабочей программ. 1.7. В техническую программу полевых опытов следует включать обоснование выбора типичных мест для расположения опытных участков, учитывающего инженерно-геологические и в их комплексе геокриологические условия, конструктивные особенности сооружения и его расположение, особенности ведения строительных работ и прогноз изменения геокриологических условий на расчетные периоды строительства и эксплуатации сооружений, а также основные положения методики и техники выполнения исследований, разрабатываемые с учетом особенностей конкретного объекта. 1.8. Опыты необходимо проводить по рабочей программе, в которой определяется объем исследований, методика и техника проведения опытов и обработки их результатов. 1.9. Опытным работам должна предшествовать специализированная инженерно-геологическая документация трещиноватости опытных камер и участков непосредственного приложения нагрузок. Инженерно-геологическая документация опытных участков выполняется и после опытов, целью которых является документация поверхности разрушения. Для условий испытания скальных и полускальных грунтов в мерзлом состоянии документация опытных участков выполняется, используя положения, данные в приложении 6. 1.10. При проведении экспериментальных исследований необходимо составить проект выполнения подготовительных строительно-монтажных работ и монтажа опытной установки, а также специальные инструкции на проведение работ. 1.11. При проведении испытаний методом кольцевого нагружения мерзлых грунтов в массиве должны учитываться следующие особенности проведения опытов: необходимость применения высокоточных измерительных приборов, надежно работающих в условиях отрицательных и переменных температур, прошедших специальную тарировку, необходимость проведения опытов на мерзлой породе (при естественном или прогнозируемом температурно-влажностном режиме) и после ее оттаивания. Примечание. В настоящих Рекомендациях не рассматривается методика определения динамических характеристик грунтов. Статические испытания МКН необходимо сопровождать динамическими испытаниями. Методика проведения динамических испытаний мерзлых и оттаявших грунтов дана в [33], а для грунтов в немерзлом состоянии в [40]. 1.12. На полевые опытные работы должен составляться проект, включающий рабочие чертежи и сметы на выполнение подготовительных строительно-монтажных работ, а также на монтаж опытной установки и проведение опытов. 1.13. На проведение опытов следует составлять специальные инструкции, учитывающие конкретные условия выполнения исследований и требования настоящих Рекомендаций. В инструкции необходимо определить: а) приемы подготовки опытных участков и площадок и технические требования к ним; б) последовательность и приемы монтажа и демонтажа опытной установки; в) требования и способы установки и проверки измерительных приборов; г) последовательность операций по изменению нагрузок; д) способы и последовательность снятия показаний измерительных приборов; е) форма ведения журналов наблюдения за ходом выполнения опыта; ж) правила безопасности ведения подготовительных и экспериментальных работ. 1.14. Полевые и лабораторные исследования реологических свойств грунтов МКН следует сопровождать определениями физико-механических свойств образцов (температура, льдистость, влажность до и после опыта, параметры сопротивления сдвигу, прочность на одноосное сжатие, деформируемость и т.д.), а также определениями динамических характеристик грунтов сейсмоакустическим методом по методикам [33, 40]. 2. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ2.1. Характеристики напряженно-деформированного состоянияσ - нормальное напряжение, давление (σс - сжимающее, σр - растягивающее, σв - разгрузки, Δσj - на ступени нагружения или, разгрузки, σвп - нормальное напряжение полной разгрузки), МПа; τ - касательное напряжение (Δτj - на ступени нагружения или разгрузки), МПа; σv = (σ1 + σ2 + σ3)/3 - среднее нормальное напряжение (σvc - при сжатии, σvp- при растяжении, σvв - при разгрузке, Δσvj - на ступени нагружения или разгрузки), МПа; σ1 > σ2 > σ3 - главные нормальные напряжения, МПа;
μσ = (2σ2 - σ1 - σ3)/(σ1 - σ3)- параметр вида напряженного состояния Надаи-Лоде; εv = ε1 + ε2 + ε3 - относительная деформация объема (εvc - при сжатии, εvв - при разгрузке, εvр - при растяжении, εvt - изменяющаяся во времени, εv0 - условно-мгновенное значение, εv¥ - стабилизированное значение, Δεj - на ступени нагружения или разгрузки); ε1 > ε2 > ε3 - относительная линейная деформация (εс - при сжатии, εв- при разгрузке, εp - при растяжении, εt- изменяющаяся во времени, ε0 - условно-мгновенное значение, ε¥ - стабилизированное значение, Δεj - на ступени нагружения или разгрузки); εDvt - изменяющаяся во времени относительная деформация объема на девиаторном участке нагружения - «дилатансия»; γt - изменяющаяся во времени относительная угловая деформация (γ0 - условно-мгновенное значение, γ¥ - стабилизированное значение, Δγj - на ступени нагружения или разгрузки);
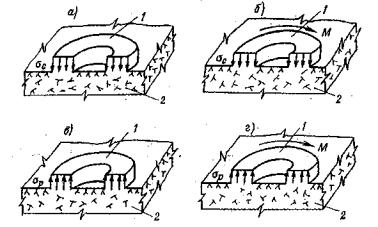
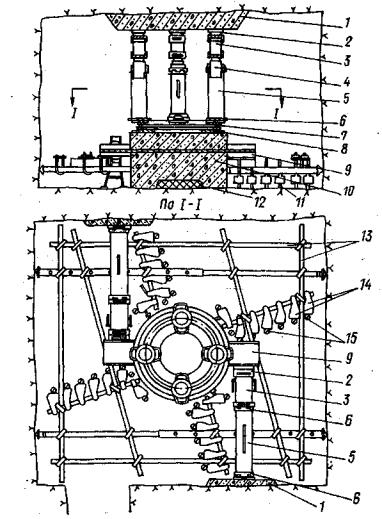
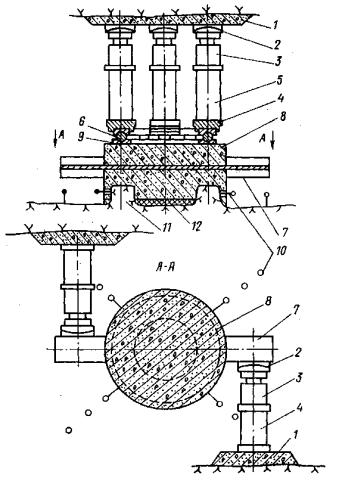
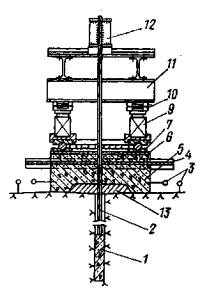
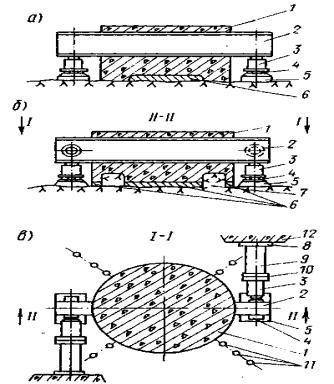
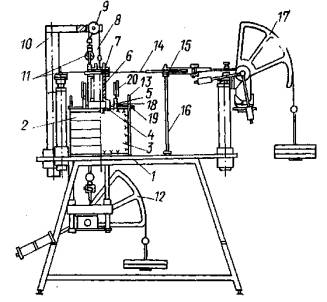
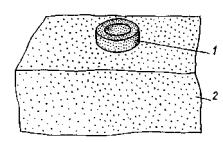
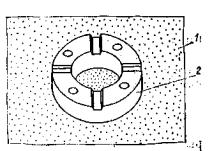
με = (2ε2 - ε1 - ε3)/(ε1 - ε3) - параметр вида деформированного состояния Надаи-Лоде; Sшt - изменяющаяся во времени осадка основания кольцевого штампа или целика (Sшсt - при нагружении, Sшвt - при разгрузке, ΔSшj - на ступени нагружения или разгрузки, ΔSш0 - условно-мгновенное значение, ΔSш¥ - стабилизированное значение), м; Srt - изменяющаяся во времени осадка поверхности массива за пределами действия кольцевой нагрузки (Srct - при нагружении, Srвt - при разгрузке, Sr0 - условно-мгновенное значение, ΔSr¥ - стабилизированное значение, ΔSrj - на ступени нагружения или разгрузки), м; Uшt - изменяющийся во времени подъем основания кольцевого штампа или целика при действии растягивающей нагрузки (Uш0 - условно-мгновенное значение, Uш¥ - стабилизированное значение, ΔUшj - на ступени нагружения), м; Urt - изменяющийся во времени подъем поверхности массива за пределами действия кольцевой растягивающей нагрузки (Ur0 - условно-мгновенное значение, Ur¥ - стабилизированное значение, ΔUrj - на ступени нагружения), м; δшt - изменяющееся во времени угловое (горизонтальное) перемещение поверхности массива (внешнего контура кольцевого целика или штампа при r = г2 (δш0 - условно-мгновенное значение, δш¥ - стабилизированное значение, Δδшj - на ступени нагружения, δrt- за пределами действия кольцевой нагрузки), м; SDшt - переменное во времени значение осадки или подъема основания кольцевого штампа или целика при действии кольцевой касательной нагрузки (ΔSDшt - на ступени нагружения), м; М - крутящий момент, Нм; Pwin - нормативное внутреннее давление воды в туннеле, МПа; 2.2. Параметры деформируемости и ползучестиEt - переменное во времени значение модуля деформации (Ect- при сжатии, Eвt - при разгрузке, Ерf - при растяжении; Ес0, Ев0, Eр0 - условно-мгновенное значение; Ес¥, Ев¥, Ер¥ - стабилизированное значение, Etj - на ступени нагружения или разгрузки), МПа; Gt - переменное во времени значение модуля сдвига (G0 - условно-мгновенное значение, G¥ - стабилизированное значение, Gtj - на ступени нагружения или разгрузки), МПа; v - коэффициент относительной поперечной деформации (коэффициент Пуассона). Evt = Et (1 - 2v) - переменное во времени значение модуля объемной деформации (Evct- при сжатии, Evвt - при разгрузке, Evpt - при растяжении; Evc0, Evв0, Evp0 - условно-мгновенное значение; Evc¥, Evв¥, Ecp¥ стабилизированное значение, Evtj - на ступени нагружения или разгрузки), МПа; Kot - переменное во времени значение удельного коэффициента отпора (Ko0 - условно-мгновенное значение; Ko¥ - стабилизированное значение), МПа/м; At - коэффициент деформации (A0 - условно-мгновенное значение, А¥ - стабилизированное значение), МПа; m < 1 - коэффициент упрочнения; θП - параметр ползучести (θПσ - при сжатии, θПp - при растяжении, θПВ - при разгрузке, θПτ -при сдвиге, θПj - на ступени нагружения), МПа-1; λ - параметр ползучести (λσ -при сжатии, λp - при растяжении, λв - при разгрузке, λτ - при сдвиге, λj - на ступени нагружения), сут-1; Т - параметр ползучести (Tσ - при сжатии, Тр - при растяжении, Тв - при разгрузке, Tτ - при сдвиге, Tj - на ступени нагружения), сут; Ecкt - переменное во времени значение модуля деформации образца грунта (Ecк0 - условно-мгновенное значение, Еск¥ - стабилизированное значение), МПа; vk - коэффициент Пуассона образца грунта. 2.3. Параметры прочностипр τ - предельное касательное напряжение (пр τ0 - условно-мгновенное значение, пр τ¥ - предельно-длительное значение (предел длительной прочности), τr - остаточная прочность), МПа; пр τi - предельное значение интенсивности касательных напряжений (пр τi0 - условно-мгновенное значение, пр τi¥ - предельно-длительное значение), МПа. φ - угол внутреннего трения (φ0 - условно-мгновенное значение, φ¥ - предельно-длительное значение, φr - остаточное значение), град. С - сцепление (С0 - условно-мгновенное значение, С¥ предельно-длительное значение, Сr - остаточное значение), МПа; пр σр - прочность на растяжение (отрыв) (пр σр0 - условно-мгновенное значение, пр σр¥ - предельно-длительное значение, пр σop - образца, пр σмp - в массиве), МПа; пр σс - прочность на одноосное сжатие (пр σс0 - условно-мгновенное значение, пр σс¥ - предельно-длительное значение (предел длительной прочности на одноосное сжатие), пр σoс - образца, пр σмс - в массиве), МПа; 2.4. Физические величиныt - время, сут; vp - скорость распространения продольных упругих волн, км/с; 2.5. Геометрические величиныr1 - внутренний радиус кольцевого целика или штампа (кольцевой нагрузки); r2 - наружный радиус кольцевого целика или штампа (кольцевой нагрузки); d - наружный диаметр кольцевого целика или штампа; r1/r2 - относительная ширина кольцевой нагрузки; Hса - активная зона деформирования при сжатии и при растяжении; Нка - активная зона деформирования при кручении; а - средний размер блока грунта. 3. ВЫБОР И ПОДГОТОВКА ОПЫТНЫХ УЧАСТКОВ3.1. Исследование реологических свойств скальных и полускальных грунтов в мерзлом состоянии и после их оттаивания следует проводить на специально подготовленных опытных участках, в штольнях, шахтах, камерах. 3.2. Опытные участки должны располагаться в наиболее характерных по составу и степени сохранности, криогенному строению и температурному режиму зонах массива, важных для расчета конкретного сооружения. 3.3. При определении размеров опытных участков следует исходить из габаритов кольцевого штампа или целика (см. п. 4.3) и конструкции опытной установки, условий монтажа, демонтажа и транспортировки ее узлов, требований размещения измерительной аппаратуры, а также требований техники безопасности при выполнении подготовительных и экспериментальных работ. 3.4. Общее количество опытов следует определять в каждом случае, исходя из конкретной инженерно-геологической обстановки и типа подземного сооружения. 3.5. Для устранения взаимного влияния, расстояния в свету между соседними штампами (целиками) следует назначать не менее полуторного диаметра штампа или целика. 3.6. Проходку опытных участков взрывным способом необходимо производить, соблюдая меры, ограничивающие образование новых трещин в массиве и нарушение температурно-влажностного режима пород. При этом необходимо ограничивать длину шнуров, вес взрывчатых веществ и их бризантность, а также количество одновременно взрываемых шпуров. Часть породы, прилегающую непосредственно к поверхностям, на которых будут располагаться опытные площадки со штампами или целиками, следует разбирать без применения взрывов (при помощи отбойных молотков, перфораторов, клиньев и т.д.). Рекомендуется, чтобы этот защитный слой составлял не менее 50 см. 3.7. Выбор на опытном участке местоположения конкретных площадок (точек) для проведения опытов надлежит производить комиссией на основе анализа инженерно-геокриологических условий участка строительства подземного сооружения в целом, детальной инженерно-геологической документации опытной площадки и осмотра выработок и площадок на месте. В комиссию должны быть включены главный геолог объекта, представители проектной, строительной и исследовательской организаций. 3.8. На выбранных площадках (точках) необходимо выполнить подготовительные работы, включающие окончательную доборку породы, составление подробной инженерно-геологической и микротопографической документации, а также необходимые буровые и строительные работы, а в необходимых случаях теплоизоляционные мероприятия. 3.9. При подготовке опытных участков необходимо руководствоваться следующими требованиями: а) на месте устройства кольцевого штампа или кольцевого целика поверхность следует сделать горизонтальной или придать ей однообразный уклон. Все отслаивающиеся и расшатанные отдельности, а также продукты выветривания породы (мелкозем, ожелезненные пленки и т.д.) с поверхности следует удалить. Высота неровностей (шероховатостей) должна соответствовать естественной, но не более 10-15 см; б) при подготовке опытных площадок в мерзлых породах и в оттаявших породах, быстро разрушающихся в результате разгрузки и изменения температурно-влажностного режима, таких как некоторые разновидности сланцев, аргиллита и т.д., необходимо подготовленную поверхность сразу же закрыть теплогидрозащитным слоем (пенопластом, песком, брезентом или пленкой), который удаляется только непосредственно перед бетонированием штампа или оголовка целика. 3.10. При подготовке кольцевых целиков необходимо руководствоваться следующими указаниями: а) кольцевой целик рекомендуется обуривать но периметру, а оставшиеся перемычки перепиливать; б) высоту кольцевого целика рекомендуется принимать не менее 30 см; 3.11. В процессе выполнения подготовительных работ необходимо составлять исполнительные документы (чертежи, схемы, зарисовки) на буровые, строительные и другие работы. 4. СХЕМЫ ИСПЫТАНИЙ И УСТАНОВКИ ДЛЯ ПРОВЕДЕНИЯ ОПЫТОВ4.1. Определение реологических свойств скальных и полускальных грунтов в мерзлом, оттаявшем и немерзлом состоянии при различных напряженных состояниях выполняется на основе схем испытаний, представленных на рис. 1. По специальной программе выполняется последовательное нагружение исследуемого массива кольцевой нормальной сжимающей (рис. 1, а) и кольцевой нормальной сжимающей и касательной нагрузкой (рис. 1, б). По схеме рис. 1, в выполняется нагружение кольцевой растягивающей, а по схеме рис. 1, г кольцевой растягивающей и касательной нагрузкой. Рис. 1. Принципиальные схемы испытаний методом кольцевого нагружения при действии: а) кольцевой нормальной сжимающей нагрузки; б) кольцевой нормальной сжимающей и касательной нагрузок; в) кольцевой нормальной растягивающей нагрузки; г) кольцевой нормальной растягивающей и касательной нагрузок. 1 - кольцевой целик скального или полускального грунта или кольцевой бетонный штамп; 2 - исследуемый массив грунта. Рис. 2. Схема установки для испытания скальных и полускальных грунтов в подземной камере кольцевым бетонным штампом 1 - бетонный упор; 2 - сферический шарнир; 3 - гидравлический домкрат; 4 - винтовой домкрат; 5 - удлиняющая труба; 6 - башмак; 7 - упорный подшипник; 8 - распределительная плита; 9 - закладная двутавровая балка; 10 - кольцевой бетонный штамп; 11 - реперы; 12 - низкомодульная прокладка; 13 - прогоны реперной рамы; 14 - держатели индикаторов; 15 - индикаторы. Рис. 3. Схема установки для испытания скальных и полускальных грунтов в подземной камере кольцевым целиком 1 - бетонный упор; 2 - сферический шарнир; 3 - гидравлический домкрат; 4 - башмак; 5 - удлиняющая труба; 6 - упорный подшипник; 7 - закладная двутавровая балка; 8 - бетонный оголовок; 9 - распределительная плита; 10- репер; 11 - кольцевой целик; 12 - низкомодульная прокладка. 4.2. Для проведения опытов на поверхности исследуемого массива (монолита) подготовляется кольцевой целик породы или кольцевой бетонный штамп. 4.3. Размер целиков (штампов) в плане следует назначать с учетом трещиноватости (блочности) исследуемого массива из условия квазиоднородности d/a ≥ 5 [42, 49], где d - наружный диаметр целика (штампа), а - средний размер блока породы (в приведении к кубической форме). Рекомендуемый диаметр кольцевого целика (штампа) для полевых опытов 1 м, при соотношении внутреннего диаметра к наружному 0,5; для лабораторных опытов 0,1 м при соотношении внутреннего диаметра к наружному 0,6.
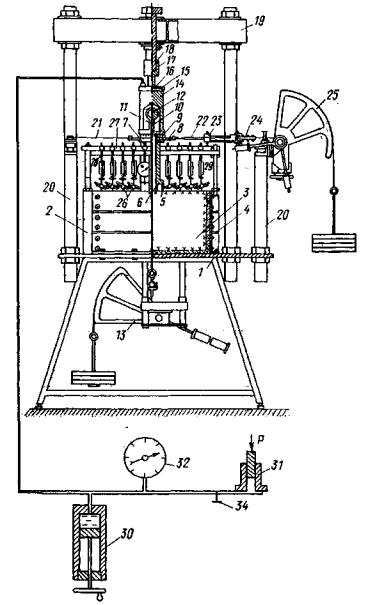
4.4. С целью получения полных данных о реологических свойствах исследуемой разности породы в мерзлом или оттаявшем состоянии при различных напряженных состояниях количество опытов надлежит принимать не менее пяти (без учета повторности). В программу испытаний должны быть включены следующие опыты - на растяжение (отрыв), на кручение при растяжении, на кручение без нормальной нагрузки и два опыта на кручение при различных нормальных сжимающих нагрузках. Общее количество опытов на строительной площадке и величину максимального нормального напряжения в опытах следует определять в каждом конкретном случае, исходя из инженерно-геологической обстановки и типа сооружения. Руководствуясь указаниями СНиП 2.02.02-85, опыты должны проводиться с трехкратной повторяемостью. 4.5. Конструкции установок для проведения полевых опытов должны обеспечивать нормальные и касательные нагрузки на основание ступенями давления 0,1 ÷ 0,5 МПа (1 ÷ 5 кг/см2) центральную передачу усилий на целик (штамп), постоянство во времени каждой ступени давления; замер перемещений поверхности массива с точностью 1·10-5 ÷ 1·10-6 м, используя стандартные индикаторы часового типа с точностью 0,01 мм и 0,001 ÷ 0,002 мм. Конструктивная схема установки может быть принята различной в зависимости от наличия оборудования и местных условий. Конструктивную схему установки, представленную на рис. 2 и 3, следует использовать при испытаниях в специальных подземных камерах размером в плане 4 × 4 м и высотой 2,5 м. Для испытаний в камерах больших размеров по высоте и на открытых площадках следует применять схемы, представленные на рис. 4 и 5. Для проведения испытаний на растяжение (отрыв) или на сдвиг кручением при растяжении следует применять конструкцию установки, представленную на рис. 6. Нагрузочные гидравлические системы установки должны быть оборудованы автоматической системой поддержания постоянного давления.
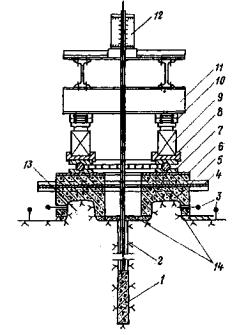
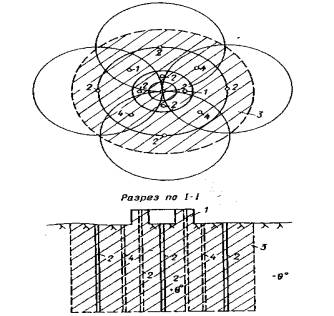
Рис. 6. Схема полевой установки для испытания скальных и полускальных грунтов на растяжение (а) и кручение при растяжении (б), (в) 1 - бетонный штамп или бетонный оголовок целика; 2 - закладная двутавровая балка; 3 - гидравлический домкрат; 4 - подшипник; 5 - бетонная подготовка; 6 - низкомодульная прокладка; 7 - кольцевой целик породы; 8 - подпятник; 9 - удлинительная труба; 10 - сферический шарнир; 11 - реперы; 12 - бетонный упор. 4.6. Высоту армированного кольцевого бетонного штампа следует принимать не менее 0,7 м, а высоту армированного бетонного оголовка кольцевого целика не менее 1 ÷ 1,2 м. Бетон необходимо укладывать на очищенную и продутую поверхность породы. При бетонировании на основание укладывается низкомодульная прокладка (деревянный щит) размером в плане равном внутренней полости кольцевого целика или штампа, и толщиной не менее 10 см для исключения контакта бетона и породы на этом участке. При бетонировании оголовка кольцевого целика прокладка толщиной 2 ÷ 4 см укладывается и с внешней стороны целика. Используется бетон не ниже марки В 20. Для испытания породы в мерзлом состоянии используются специальные марки бетона, твердеющие при отрицательной температуре. Укладку бетона и отбор образцов для определения его прочности надлежит выполнять на основе соответствующих технических условий и инструкций. Примечание. При подготовке опытов в случае испытания пород в мерзлом состоянии в полевых условиях бетонный штамп или оголовок кольцевого целика изготавливается с учетом требований по возведению обделки строящегося сооружения на основе Рекомендаций ВСН 36-86 [6]. Нагруженне основания следует выполнять после набора бетоном заданной прочности и выравнивания температуры основания штампа или целика до температуры окружающего массива. 4.7. Определение размера закладной балки и армирование штампа или оголовка выполняются на основе специального расчета исходя из максимальных усилий, предусмотренных программой испытаний. 4.8. Устройство целиков (штампов) при испытании пород в мерзлом состоянии выполняется при обязательном сохранении естественного или прогнозируемого температурного режима исследуемого массива. Контроль температурного режима массива проводится с помощью температурных датчиков, терморезисторов ММТ-4 или температурных датчиков ПТ и ПТС, устанавливаемых в специальные температурные скважины (рис. 7). 4.9. Устройство целиков (штампов) при испытании пород в талом состоянии выполняется после предварительного оттаивания исследуемого массива. Для оттаивания массива рекомендуется использовать глубинный отогрев, используя теплоэлектронагреватели (ТЭНы) [35], устанавливаемые в специально пробуренные шпуры или скважины. Рекомендуемая схема отогрева представлена на рис. 7. Размеры зоны оттаявшего массива должны быть не менее двух диаметров целика или штампа по глубине и трех диаметров в плане и должны поддерживаться в процессе конкретного опыта. Расчет времени отогрева массива и количества нагревательных элементов выполняется на основе специального теплотехнического расчета [41]. 4.10. Контроль глубины оттаивания породы под целиком или штампом проводится с помощью температурных датчиков.
Рис. 7. Схема глубинного отогрева массива 1 - кольцевой целик или кольцевой бетонный штамп; 2 - скважина с глубинным теплоэлектронагревателем (ТЭН); 3 - зона оттаявшего массива; 4 - температурные скважины. В специальных скважинах датчики, смонтированные в связи через 10 см и установленные в шпур (скважину), должны быть по всей глубине тщательно гидроизолированы глинистым грунтом, чтобы предотвратить попадание воды, образующейся при оттаивании породы. Результаты температурных замеров заносятся в журналы наблюдений. 4.11. Конструктивная схема лабораторной установки для испытания монолитов скальных и полускальных грунтов в мерзлом и оттаявшем состоянии представлена на рис. 8. Максимальный размер монолита в плане 0,50×0,50 м. Исследуемый монолит породы помещается в секционный лоток, устанавливаемый на станине установки. Жесткое закрепление монолита в лотке достигается путем погружения его в цементно-песчаную оболочку. На рабочей поверхности монолита выполняется кольцевой целик или кольцевой бетонный штамп заданных размеров в плане. При проведении опытов на схеме (рис. 1, а, б) приложение нормального сжимающего или касательного напряжения на рабочую поверхность монолита осуществляется при помощи рычажно-гидравлических систем. Нагрузочные системы стенда обеспечивают создание на контакте целика или штампа (с рабочей кольцевой площадью 50 см2) с основанием нормальных напряжений до 5 МПа (50 кг/см2) и касательных напряжений до 15 МПа (150 кг/см2). Указания по тарировке нагрузочных систем стенда даны в приложении 3.
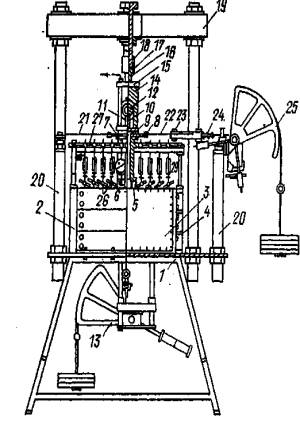
Рис. 8. Конструкция стенда для испытания монолитов скальных и полускальных грунтов методом кольцевого нагружения 1 - станина; 2 - секционный лоток; 3 - монолит породы; 4 - бетонная оболочка; 5 - кольцевой целик или кольцевой бетонный штамп; 6 - металлическое кольцо; 7 - переходный цилиндр; 8 - диск кручения; 9 - упорный подшипник; 10 - штамп; 11 - шарик; 12 - нагрузочная рама; 13 - рычаг приложения нормальной нагрузки; 14 - цилиндр; 15 - гидравлическая камера; 16 - крышка; 17 - переходник; 18 - упорный винт; 19 - упорная рама; 20 - стойки; 21 - трос; 22 - распределительный диск горизонтального усилия; 23 - ось; 24 - вилка; 25 - рычаг приложения крутящего момента; 26 - реперы; 27 - измерительная рама; 28 - держатель индикатора; 29 - индикаторы часового типа.
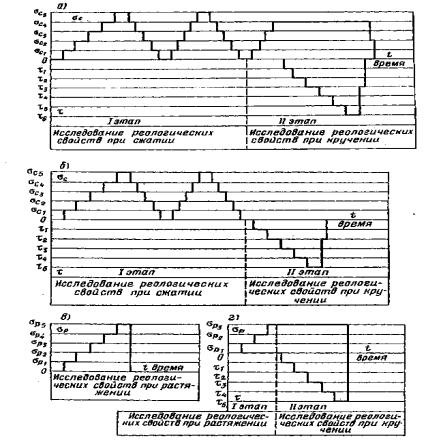
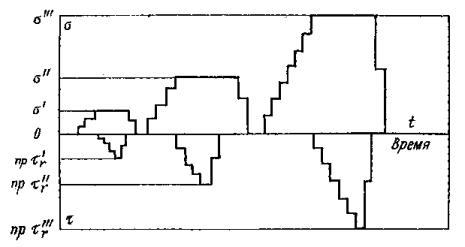
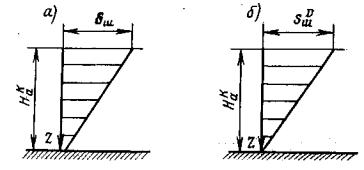
Рис. 9. Конструкция стенда для испытания монолитов скальных и полускальных грунтов на растяжение и на кручение при растяжении 1 - станина; 2 - секционный лоток; 3 - монолит; 4 - кольцевой целик или кольцевой бетонный штамп; 5 - металлическое кольцо; 6 - переходный цилиндр; 7 - диск кручения; 8 - трос; 9 - блок; 10 - консоль; 11 - рама приложения вертикальной нагрузки; 12 - рычаг вертикальной нагрузки; 13 - стойки; 14 - трос; 15 - распределительный диск горизонтального усилия; 16 - подставка; 17 - рычаг приложения горизонтальной нагрузки (крутящего момента); 18 - реперы; 19 - держатели индикаторов; 20 - индикаторы часового типа. 4.12. Для испытания пород подсхеме (рис. 1, б, в) конструктивная схема лабораторной установки представлена на рис. 9. 4.13. Полевые и лабораторные опыты сопровождаются сейсмоакустическими исследованиями с целью последующего распространения результатов испытаний на массив, вмещающий сооружения. Методика проведения полевых сейсмоакустических исследований дана в [33, 40]. При испытании монолитов пород в лабораторных условиях проводится их геофизическое обследование по трем взаимно перпендикулярным направлениям непосредственно перед установкой в лоток стенда. В случае отбора монолита мерзлого грунта выполняется детальное описание его криогенного строения по горизонтальной поверхности и боковому срезу, сопровождаемое масштабным фотографированием и отбором проб на льдистость и влажность. После проведения опыта на оттаявшем монолите выполняется послойное определение его влажности. Испытание монолита мерзлого грунта выполняется в криогенной лаборатории (камере) с заданной постоянной отрицательной температурой. Контроль за температурой монолита грунта осуществляется с помощью термопар, расположенных в нескольких точках по его высоте. 5. ПРОВЕДЕНИЕ ИСПЫТАНИИ5.1. Опыты по определению реологических свойств скальных и полускальных грунтов в мерзлом состоянии и после их оттаивания при различных напряженных состояниях в зависимости от рабочей программы конкретного эксперимента должны включать создание в плоскости контакта целика (штампа) с исследуемым массивом нормальных сжимающих напряжений в три этапа (рис. 10, а). В процессе проведения каждого этапа нагрузки должны увеличиваться ступенями до заданной интенсивности. На третьем этапе при достижении заданной величины нормальное напряжение поддерживается постоянным при последующем приложении крутящего момента: - создание в плоскости контакта целика (штампа) с массивом касательных напряжений, величина которых в ходе опыта увеличивается ступенями вплоть до наступления предельного состояния (рис. 10, а). Опыты производятся при заданном программой нормальном напряжении (рис. 10, а), либо при отсутствии нормального напряжения (рис 10, б); - создание в плоскости контакта растягивающих напряжений, величина которых в ходе опыта увеличивается ступенями вплоть до наступления предельного состояния (рис. 10, в); - создание в плоскости контакта растягивающего напряжения до заданной интенсивности, меньшей предельной величины, которое при последующем приложении касательных напряжений поддерживается постоянным (рис. 10, г). Примечание. Максимальная величина нормального напряжения в опытах устанавливается на основе предварительных расчетов напряженного состояния массива и в зависимости от конкретных условий взаимодействия его с подземной конструкцией (глубина заложения подземного сооружения, величина давления, оказываемого на массив и т.д.). Рекомендуется проводить испытания при максимальной величине нормального напряжения не менее 4,0 МПа. 5.2. Изменение интенсивности нагрузки при проведении опытов рекомендуется осуществлять по диаграммам, представленным на рис. 10, с учетом следующих требований: - максимальное нормальное напряжение не должно превышать принятое для данной серии опытов; - все интервалы и изменения напряжении при проведении испытаний следует разбивать на 4-6 ступеней (σI, II, III и т.д., τI, II, III
Рис. 10. Программы изменения нормальных и касательных напряжений при проведении опытов. Изменение интенсивности давления между ступенями при отсутствии специальных требований следует производить со скоростью не более 0,5 МПа в 1 мин. Примечания. 1. При проведении опытов на растяжение допускается разбивка интервала нагружения на 2-3 ступени. 2. Рекомендуется назначать программу нагружения в полевых опытах на основе результатов лабораторных испытаний монолитов МКН. 3. Величина ступени нагружения не должна превышать 1,0 МПа при действии нормальной нагрузки и 0,5 МПа при действии касательной нагрузки. 5.3. Разгрузку рекомендуется производить теми же ступенями, что и принятыми в режиме нагружения. 5.4. Расчет величины среднего нормального напряжения σ на контакте целика (штампа) с основанием производится по зависимости
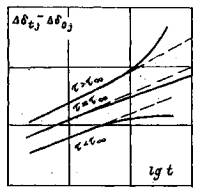
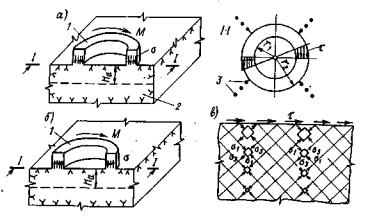
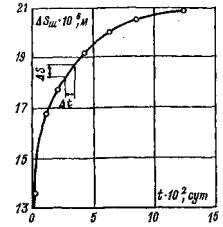
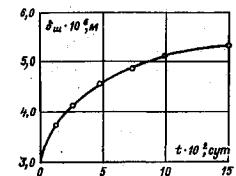
где Р - нормальная нагрузка, создаваемая домкратами в полевых испытаниях или нагрузочной системой в лабораторных опытах; N - вес системы приложения вертикальной нагрузки (в опытах на растяжение величина N берется со знаком.«-»); r1, r2 - соответственно внутренний и наружный радиусы кольцевого целика (штампа) в плоскости контакта с массивом. 5.5. Расчет величины среднего касательного напряжения т на контакте целика (штампа) с массивом производится по величине крутящего момента τ = M (1 + ξ)/πr32 (1 - ξ) (2) где ξ = r1/ r2; M - крутящий момент. 5.6. При достижении предельного состояния и при повторных сдвигах по образовавшейся поверхности разрушения (трещине) величина среднего касательного напряжения определяется по зависимости пр τ = 3 M пр/2π (r32 – r21). (3) 5.7. Приложение кольцевой касательной нагрузки должно осуществляться ступенями, составляющими 5 ÷ 20 % от нормального напряжения. Примечание. По мере приближения к предельному состоянию величину ступеней следует уменьшать. 5.8. На каждой ступени давление поддерживается постоянным в течение времени, необходимого для достижения условной стабилизации деформаций, если процесс развития деформаций во времени имеет затухающий характер, или в течение определенного периода времени, если процесс имеет незатухающий характер. Первый отсчет по измерительным приборам должен браться сразу же после достижения назначенного уровня давления на ступени, второй и последующие через 5, 10, 20, 30, 60 и 120 мин. и т.д., но не реже, чем через 12 часов. Результаты замеров перемещений заносятся в специальные журналы наблюдений (Приложение 9). Контроль стабилизации деформаций рекомендуется осуществлять путем оперативного построения графика в осях Ut – lg t, либо δt – lg t; St – lg t, в зависимости от конкретной программы опыта, по величине среднего перемещения реперов, установленных на штампе (целике) (рис. 11).
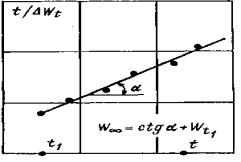
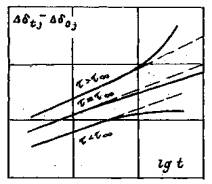
При затухающем характере развития деформаций во времени на ступени нагружения (кривая 1, рис. 11) выполняется построение графика в осях t – t1/ΔWt - t (рис. 12), где ΔWt = Wt – Wt1; Wt - перемещение штампа (целика) в момент времени t; Wt1 - перемещение в момент времени t1 = 2 ÷ 3 ч с момента нагружения (разгрузки) ступени давления. В зависимости от программы опытов под величиной Wt на рис. 11 и 12 условно подразумевается осадка, подъем или горизонтальное (угловое) перемещение поверхности массива. В данном случае выдерживание на ступени постоянного давления считается законченным, если отношение (W¥ - Wt)/W¥ не превышает 0,1, где W¥ - стабилизированная величина перемещения при времени выдерживания постоянного давления на ступени, стремящемся к бесконечности, т.е. ставится условие, чтобы замеренное в опыте перемещение отличалось от перемещения, соответствующего полной стабилизации, не более чем на 10 процентов. При незатухающем характере развития деформаций во времени (кривая 2, рис. 11) выдерживание на ступени считается законченным, если при трех последующих двухчасовых отсчетах сохраняется вид зависимости 2 на рис. 11. Примечания. 1. С целью сокращения общего времени проведения полевых опытов, критерии стабилизации следует уточнять на основе выполнения опытов в лабораторных условиях по результатам испытания монолитов пород, отобранных из областей массива, максимально приближенных к местам проведения полевых испытаний. 2. Следует в процессе приложения кольцевой касательной нагрузки анализ горизонтальных (угловых) перемещений штампа (целика) во времени дополнять анализом вертикальных перемещений массива (рис. 13). Как правило, при затухающем характере развития горизонтальных (угловых) перемещений наблюдается осадка поверхности массива во времени (кривая 1, рис. 13), а при незатухающем - подъем поверхности основания (кривая 2, рис. 13). 3. Wt в момент времени t определяется как средняя величина перемещения штампа (целика), зафиксированная по реперам, расположенным на штампе (целике). Величина перемещения Wt на расстоянии r от штампа (целика) определяется как средняя величина перемещений реперов, расположенных на расстоянии r от штампа (целика).
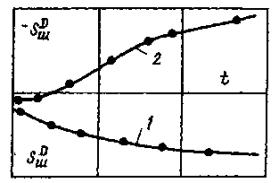
Рис. 13. Зависимости дополнительной осадки (подъема) поверхности основания от величины касательного напряжения 1 - при затухающей ползучести; 2 - при незатухающей ползучести. 5.9. После достижения предельного сопротивления сдвигу (срезу) опыт необходимо продолжать для определения величины сдвигающего усилия, которое характеризует остаточное сопротивление сдвигу по образовавшейся трещине. Момент достижения остаточного сопротивления породы сдвигу рекомендуется определять по графику смещений целика (штампа).
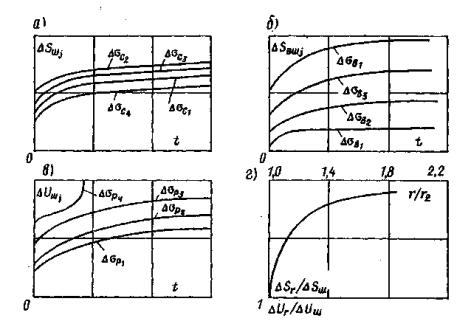
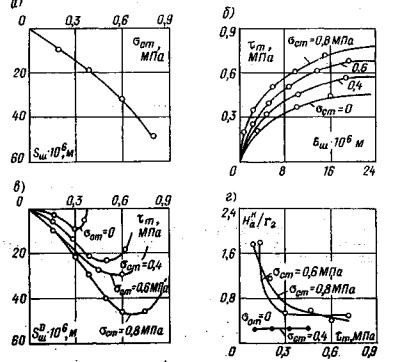
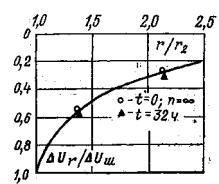
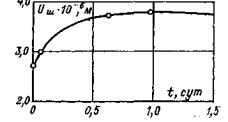
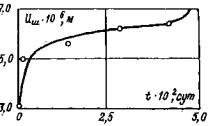
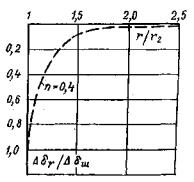
Рис. 14. Программа изменения нормальных и касательных напряжений при повторных сдвигах кольцевого целика (штампа) по образовавшейся после среза трещине 5.10. Рекомендуется в каждом опыте выполнять повторные испытания сопротивляемости сдвигу пород по образовавшейся в результате первого опыта зоне разрушения (трещине) - остаточного сопротивления сдвигу. Испытания необходимо выполнять при нескольких (минимум трех) различных нормальных напряжениях (σ', σ", σ"'). Режим изменения нормальных и касательных напряжений при сдвиге приведен на рис. 14. По окончании каждого опыта на сдвиг допускается возвращать целик (штамп) в исходное положение после его полной разгрузки и повторять испытание. 5.11. Необходимо, чтобы опыты по определению предельного сопротивления сдвигу проводились при различных нормальных напряжениях (минимум трех), а сопротивление сдвигу по образовавшейся трещине (остаточное сопротивление сдвигу) при проведении повторных опытов на каждом целике (штампе) при совпадающих по величине нормальных напряжениях. 5.12. В случае, если массив в период эксплуатации сооружения будет находиться в водонасыщенном состоянии, при испытании его после оттаивания породу следует подвергать в течение 3-6 суток предварительному смачиванию водой. 5.13. Опыты на целиках (штампах) следует выполнять после набора бетоном проектной прочности и стабилизации температурного поля в основании. 5.14. После проведения испытаний целики (штампы) рекомендуется переворачивать с целью анализа характера разрушения породы. При этом рекомендуется производить микротопографическую съемку рельефа поверхности разрушения с зарисовкой трещин или ослабленных прослоек, состава заполнителя трещин и его физико-механического состава, определения льдистости. 6. ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ6.1. Результаты обработки опытов представляются в табличной и графической форме по ступеням нагружения Δσсj, Δσpj, Δτj, разгрузки Δσвj, Δτвj для каждого вида и цикла испытания с целью последующей их обработки и интерпретации. 6.2. По данным, полученным при нагружении массива нормальной нагрузкой (сжимающей или растягивающей), для каждой ступени нагружения Δσj и разгрузки Δσвj строятся зависимости осадки S (подъема U) поверхности исследуемого массива от времени (кривые ползучести) по осредненным перемещениям реперов, установленных на целике (штампе) (рис. 15, а, б, в), а также осадка (подъем) поверхности массива вокруг целика (штампа) в относительных координатах для стабилизированного состояния (рис. 15, г). Примечание. Изложенная ниже методика определения параметров ползучести при нагружении массива нормальной сжимающей нагрузкой может быть непосредственно перенесена на проведение испытаний пород сплошным штампом круглой формы в плане (т.е. при соотношении параметра ξ = r1/r2 = 0). При проведении опытов квадратным штампом для использования методики обработки опытных данных и определения параметров ползучести необходимо привести его к равновеликому по площади сплошному круглому штампу.
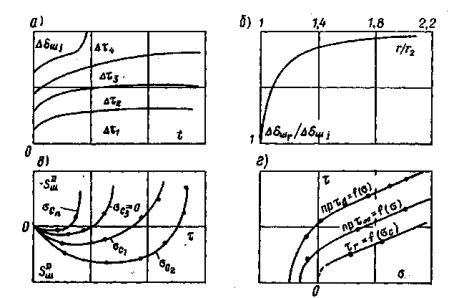
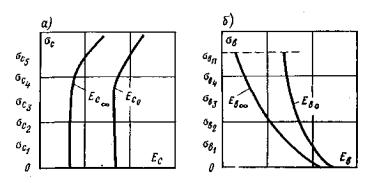
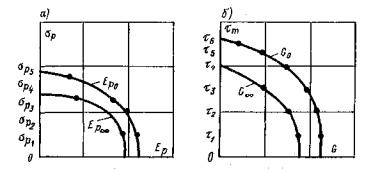
Рис. 15. Графики зависимости перемещений поверхности массива во времени от действия нормальной кольцевой нагрузки: а) при сжатии; б) при разгрузке; в) при растяжении; г) за пределами кольцевой нагрузки. Рис. 16. Графики зависимости перемещений поверхности массива во времени от действия кольцевой касательной нагрузки и сопротивления сдвигу: а) кривые ползучести; б) за пределами действия кольцевой нагрузки; в) вертикальных перемещений; г) зависимости сопротивления сколу и сдвигу. 6.3. По данным, полученным при нагружении массива кольцевой касательной нагрузкой, строятся кривые ползучести для каждой ступени Δτj (рис. 16, а), зависимости горизонтальных (угловых) перемещений поверхности основания вокруг целика (штампа) для стабилизированного состояния tст в относительных координатах (рис. 16, б), зависимости стабилизированной осадки (подъема) поверхности основания целика (штампа) от касательного напряжения т, полученные при различных нормальных напряжениях (рис. 16, в). 6.4. По данным, полученным при нагружении массива кольцевой нормальной нагрузкой; определяется значение условно-мгновенного модуля деформации при нагружении Ес0 по ступеням. В качестве расчетной используется модель основания в виде линейно-деформируемого слоя ограниченной толщины [21, 22]. Таблица 1 Таблица значений коэффициента ωс
6.5. По данным, полученным при снятии давления (разгрузке), определяется модуль условно-мгновенной деформации Eв0j при разгрузке по ступеням. 6.6. Модули условно-мгновенной деформации Ec0j и Eв0j определяются по зависимостям [22]:
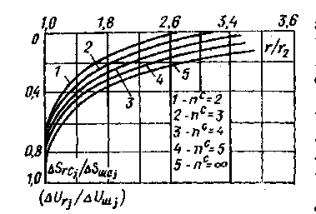
где ωc - табличный коэффициент (табл. 1), зависящий от соотношения ξ = r1/r2, размеров активной зоны деформирования Hса (толщины слоя); значение коэффициента ωc при r1/r2 = 1 в табл. 1 соответствует среднему перемещению основания в пределах площади приложения кольцевой нагрузки; v - коэффициент относительной поперечной деформации (см. п. 6.22); ΔSшс0j - условно-мгновенная осадка целика (штампа) на ступени нормального напряжения Δσ0j; ΔSшв0j - условно-мгновенное вертикальное перемещение целика (штампа) на ступени разгрузки. 6.7. В том случае, если в опыте принято соотношение ξi = r1/r2 целика или штампа, отличающееся от имеющегося в табл. 1, величина ωс определяется по зависимости ωc = ωTc/(1 – ξ2i), (6) где ωTc - табличный коэффициент для величины ξт.
Рис. 17. Номограмма для определения размера активной зоны Hас при ξ = 0,6. 6.8. При интерпретации результатов опытов за расчетную принимается величина Hса, для которой теоретическая и полученная в эксперименте формы перемещений поверхности породы (воронка) достигают наилучшего совпадения. Для этой цели используется номограмма осадки поверхности основания, построенная в относительных координатах по данным табл. 1 (рис. 17), на которую наносятся экспериментальные точки (см. приложение 5). 6.9. Определение параметров ползучести в расчетном интервале действия нормальной сжимающей нагрузки рекомендуется .выполнять, используя зависимость [20, 57].
где Еc¥ - модуль деформации при t ® ¥; θσj, vσj, Tσj - параметры ползучести, ΔSj (t) - осадка основания целика (штампа) на ступени нагружения нормальной нагрузкой в рассматриваемый момент времени t.
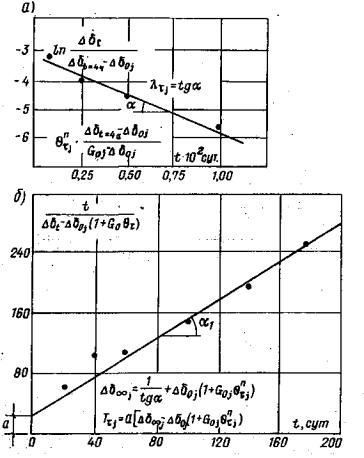
Рис. 18. Графическое определение параметров ползучести:
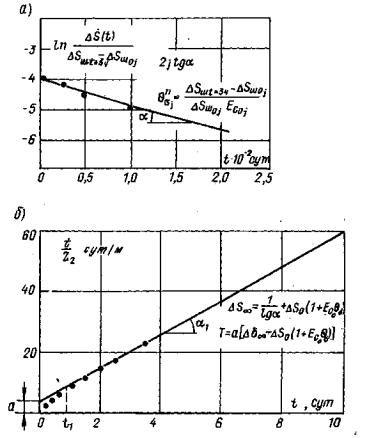
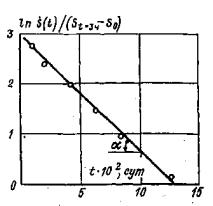
6.10. Параметры ползучести θПσj и λσj. определяются по начальному участку (до 3-4 ч с момента нагружения ступени) кривой ползучести графически (рис. 18, а), а параметр Tσj, и величина осадки ΔS¥j при t ® ¥ определяются по графику (рис. 18, б). Параметр E¥j определяется по зависимости
Примечание. Для определения параметра Tσj, а также величины ΔSшс¥j рекомендуется использовать метод наименьших квадратов. Расчет выполняется по следующим зависимостям:
где i -
число экспериментальных точек; t1 - время с момента
нагружения ступени, с которого зависимость Величина модуля деформации Ecj/t для различных моментов времени определяется по формуле
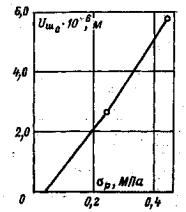
6.11. Параметры ползучести при разгрузке и величина модуля деформации Ев¥ определяются тю ступеням, используя методику, аналогичную п. 6.9 и 6.10 [19, 51]. 6.12. По данным, полученным при нагружении массива кольцевой растягивающей нагрузкой, определяется значение условно-мгновенного модуля деформации при растяжении Eр0 по ступеням нагружения, используя зависимость
где ΔUш0j - величина условно-мгновенного перемещения поверхности основания на контакте кольцевого целика (штампа) с основанием на ступени Δσpj.
Рис. 19. Графики зависимости модуля деформации от нормального напряжения: при нагружении (а) и разгрузке (б). 6.13. Определение параметров ползучести на ступени нагружения растягивающей нагрузкой аналогично изложенному в п. 6.9 и 6.10. Рис. 20. Графики зависимости модулей деформации от действующих усилий: при растяжении (а) и сдвиге кручением (б). 6.14. Результаты расчета модулей деформации при нагружении массива нормальной сжимающей или растягивающей Нагрузкой и при разгрузке рекомендуется обобщить в виде графиков (рис. 19 и 20) либо в табличной форме. Таблица 2 Таблица значений коэффициента ωk
Примечание. В том случае, если зависимости Ec0 = f (σс) и Еc¥ = f (σс) во всем исследованном интервале действия σс близки к линейным, параметры Еc0, Еc¥, θσ, λσ Тσ определяются по осредненной кривой ползучести (см. приложение 5). 6.15. По данным, полученным при нагружении массива кольцевой касательной нагрузкой, определяются значения условно-мгновенного модуля сдвига G0j,- по ступеням нагружения. В качестве расчетной используется модель основания в виде линейно деформируемого слоя ограниченной толщины.
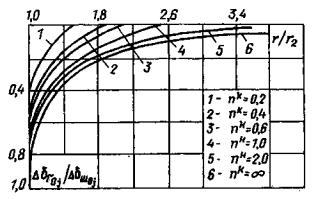
Рис. 21. Номограмма для определения размера активной зоны деформирования при кручении Hак при ξ = r1/r2 = 0,6. 6.16. Модуль сдвига G0j определяется по зависимости
где ωk - табличный коэффициент (табл. 2), зависящий от соотношения ξ = r1/r2 размеров активной зоны деформирования при кручении Hкa (толщина слоя); Δδш0j - условно-мгновенное горизонтальное (угловое) перемещение внешнего контура (при r1 = r2) кольцевого целика (штампа), соответствующее ступени нагружения Δτj. 6.17. В том случае, если в опыте принято соотношение ξj = r1/r2 целика (штампа), отличающееся от имеющихся значений в табл. 2, величина ωk определяется по зависимости ωk = ωTk (1 – ξ4i)/(1 – ξ4T), (14) где ωTk - табличное значение коэффициента для ξт. 6.18. При интерпретации результатов опытов за расчетную принимается величина Hка, для которой теоретическая и экспериментально полученная формы перемещений поверхности породы достигают наилучшего совпадения. Для этой цели используется номограмма перемещений поверхности основания, построенная в относительных координатах по данным табл. 2 (рис. 21), на которую наносятся экспериментальные точки (см. приложение 5). 6.19. Определение параметров ползучести по результатам экспериментов на каждой ступени нагружения при затухающей во времени деформации выполняется по зависимости
где G¥j, - модуль сдвига при t ® ¥, θПτj, λτj, Тτj-параметры ползучести при сдвиге; Δδ (t) - горизонтальное (угловое) перемещение внешнего контура кольцевого целика (штампа) в момент времени t.
Рис. 22. Графическое определение параметров ползучести при сдвиге кручением:
6.20. Параметры ползучести θПτ и λτ определяются по начальному участку кривой ползучести по графику на рис. 22, а, а параметр Tτ и величина горизонтального перемещения Δδш¥j при t ®¥ определяются по графику на рис. 22, б. Параметр G¥j определяется по зависимости
Примечание. Для определения параметра Тτj, а также величины Δδш¥ рекомендуется использовать метод наименьших квадратов. Расчет выполняется по следующим зависимостям:
где i -
число экспериментальных точек; t1 - время с момента нагружения
ступени, с которого зависимость 6.21. Результаты расчета модуля сдвига G0j и G¥j по ступеням нагружения рекомендуется обобщить в виде графика (рис. 20, б). Величина модуля сдвига Gj(t) для различных моментов времени определяется по формуле
6.22. Коэффициент относительной поперечной деформации определяется по зависимости
Для определения v по зависимости (20) рекомендуется использовать величину модуля сдвига G¥ полученную по первым ступеням нагружения кольцевой касательной нагрузкой при σ = 0, где зависимость δ = f (t) может быть принята линейной, а деформации имеют затухающий во времени характер (см. приложение 5).
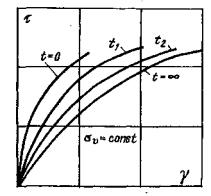
Рис. 23. Зависимости деформаций ползучести в полулогарифмических координатах. 6.23. Результаты испытаний сопротивляемости сдвигу исследуемой разности породы необходимо обобщить в виде графической зависимости величины предельных касательных напряжений от нормальных напряжений (рис. 16, г) 6.24. Следует, с целью определения предела длительной прочности породы на сдвиг и на растяжение, кривые ползучести, полученные на каждой ступени нагружения, представлять в полулогарифмических координатах (рис. 23). За предельно длительное значение сопротивления сдвигу пр τ¥ и растяжению пр σp¥ принимается максимальная величина касательного напряжения или максимальная величина растягивающего напряжения, при действии которого деформации на ступени нагружения еще имеют явно выраженный затухающий характер, т.е. Отклоняются в сторону оси lg t от линейной зависимости (см. приложение 5). 6.25. По результатам опытов, выполненных при различных нормальных напряжениях, устанавливается зависимость пр τ¥ = f (σ) (рис. 16, г). 6.26. Для определения параметров сопротивления сдвигу φ0 и С0; φ¥ и С¥ в области действия нормальных сжимающих напряжений рекомендуется использовать линейную аппроксимацию зависимостей пр τ = f (σ), а в области действия нормальных растягивающих напряжений кусочно-линейную [47] или нелинейную аппроксимацию [53]. 6.27. Результаты повторных испытаний сопротивляемости сдвигу пород по образовавшейся в результате первого опыта зоне разрушения (трещине) в зависимости от нормального напряжения следует обобщать в виде графической зависимости остаточного сопротивления сдвигу от нормального напряжения (рис. 16, г). Для определения параметров остаточного сопротивления сдвигу φr и Сr используется линейная аппроксимация зависимости τr = f (σc). 6.28. Для трансверсально-изотропных пород определяются модули деформации вдоль и поперек напластования по специальной методике, представленной в [25]. 6.29. Для пород, обладающих явно выраженной нелинейностью связи между величиной касательного напряжения и деформацией сдвига (см. приложения 1, 5), по результатам экспериментов устанавливаются следующие зависимости: εv (t) = f (σv; t), (21) γi (t) = f (σv; τi; t), (22) εDv (t) = f (σv; τi; t), (23) пр τi¥ (t) = f (σv; t), (24) где εv(t), γi(t) - соответственно изменение объемной деформации во времени и изменение интенсивности деформаций сдвига во времени; σv, τi - соответственно среднее нормальное напряжение и интенсивность касательных напряжений; εDv(t) - объемная деформация, вызванная действием девиатора напряжений (интенсивностью касательных напряжений τi) при постоянной величине σv; пр τi¥ - предельно длительное значение интенсивности касательных напряжений, характеризующее предел длительной прочности. 6.30. Деформация объема от среднего нормального напряжения при гидростатическом сжатии для произвольного момента времени принимается линейной и определяется по следующим зависимостям [58]:
где Ev0 - условно-мгновенное значение модуля объемной деформации; Ev¥ - стабилизированное значение модуля объемной деформации при t ® 0. 6.31. Рекомендуется зависимость интенсивности деформаций сдвига от интенсивности касательных напряжений при заданной величине среднего нормального напряжения σv = const для различных моментов времени определять в следующей последовательности. По значениям Gtj, определенным по ступеням нагружения (см. п. 6.21), вычисляется относительная деформация сдвига Δγj для различных моментов времени t, соответствующая приращению среднего касательного напряжения Δτj на ступени нагружения Δγtj = Δτtj/Gtj. (28)
По вычисленным значениям Δγtj строятся зависимости γt = f (τ, t) путем суммирования относительных деформаций сдвига (рис. 24).)
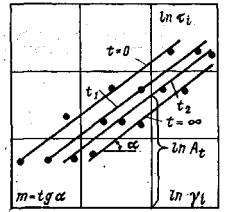
Рис. 26. Зависимости γi = f (τit) в логарифмических координатах. Так как при совместном действии кольцевой нормальной и касательной нагрузок в основании создается напряженное состояние, характеризуемое параметром вида напряженного состояния μσ = (2σ2 – σ1 – σ3)/(σ1 – σ3) = 0, то полученные зависимости γi = f (τ, t) являются зависимостями между τi и γit (рис. 25) [7]. Рекомендуется степенная аппроксимация зависимостей γi (t) = f (τi; t) в следующем виде: γi (t) = (τi/At)1/m, (29) где А - параметр деформируемости, переменный во времени; m ≤ 1 - коэффициент упрочнения. 6.32. Величина параметра At для различных моментов времени и коэффициент m определяются на основе построения зависимости γi (t) = f (τi; t) в логарифмических координатах (рис. 26). Примечание. Определение параметров At и m для конкретного момента времени t выполняется методом наименьших квадратов из решения системы двух уравнений:
где n - число экспериментальных точек.
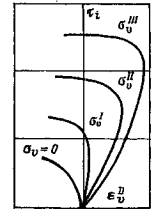
6.33. Зависимости изменения относительной деформации объема на девиаторном участке нагружения (23) (действие кольцевой касательной нагрузки) для различных моментов времени при различных нормальных напряжениях следует определять, используя экспериментальные данные, представленные на рис. 16, в (см. приложения 1 и 5). При постоянной величине σv в конкретном опыте определение приращения εDvj (t) на ступени касательного напряжения τi, выполняется, используя зависимость
где εDvj (t) - приращение относительной деформации объема на ступени Δτj; ΔSDj (t) - приращение средней осадки (подъема) поверхности массива в пределах кольцевой нагрузки на ступени Δτj; Нка - активная зона деформирования на ступени касательного напряжения (см. п. 6.18). По вычисленным значениям εDvj (t) строится зависимость εDv(t) = f (τi; σv) путем суммирования относительных деформаций объема в конкретном опыте при заданной величине σv = const. Аналогично данные зависимости определяются для других опытов, выполненных при различных значениях σс = σv. Полученные зависимости εDv(t) = f (τi; σv; t) обобщаются в виде графика (рис. 27). 6.34. По результатам опытов, выполненных при различных нормальных напряжениях, устанавливается зависимость np τi¥ = f (σv) (рис. 28). Величина пр τi¥ в каждом конкретном опыте определяется согласно п. 6.24. В области действия нормальных сжимающих напряжений рекомендуется использовать линейную аппроксимацию зависимости np τi¥ = f (σv), а в области действия нормальных растягивающих напряжений кусочно-линейную или нелинейную аппроксимацию. 6.35. Рекомендуется на начальном участке зависимости vit = f (τi) может быть принята линейной для различных моментов времени t, величину коэффициента удельного отпора Ko и его изменение во времени Коt определять по формуле [58]:
где Ko0 - условно-мгновенное значение коэффициента удельного отпора, МПа/м; Ko¥ - стабилизированные значения коэффициента отпора при t ® ¥. Примечание. Примеры расчета напряженного состояния обделок напорных туннелей с учетом ползучести даны на стр. 251-257 [44]. 6.36. При нелинейной зависимости γit = f (τi, t) (см. п. 6.31) величину коэффициента удельного отпора Ко и его изменение во времени Коt при постоянном давлении в туннеле следует определять по формуле:
где
At и m - параметры деформируемости, определяемые по зависимости γit = f (τi) при σv = 0 ПРИЛОЖЕНИЯПриложение 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Метод испытания |
φ¥ |
С¥, МПа |
Предельное сопротивление сдвигу пр τ, МПа |
|||
|
σ = 0,2, МПа |
σ = 0,4, МПа |
σ = 0,6, МПа |
σ = 0,8, МПа |
|||
|
МКН |
27°30' |
0,4 |
0,504 |
0,608 |
0,712 |
0,816 |
|
Стабилометр |
27°50' |
0,4 |
0,507 |
0,612 |
0,720 |
0,824 |
|
Одноплоскостной срез |
29°50' |
0,38 |
0,593 |
0,606 |
0,720 |
0,833 |
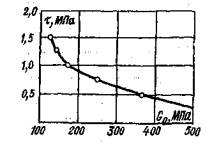
Из табл. 1 следует, что отличие в величинах предельного сопротивления сдвигу гипса по результатам испытаний в различных приборах не превышает нескольких процентов и находится в пределах точности экспериментов.
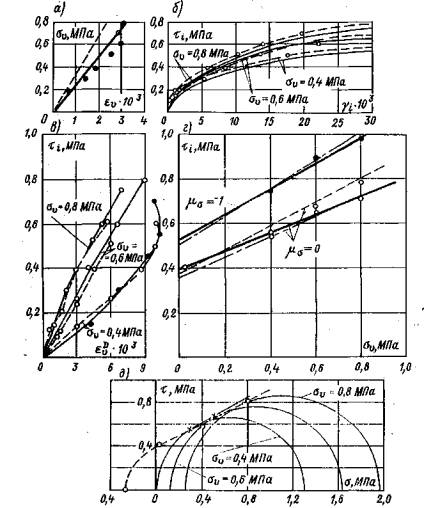
Как было показано выше, из анализа напряженного состояния в массиве при использовании МКН испытания проводятся при параметре вида напряженного состояния Надаи-Лоде μσ = 0, а при испытании в стабилометре напряженное состояние образца характеризуется параметром μσ = -1. Ниже будет показано, что в случае, если результаты испытаний, полученные при различных значениях параметра μσ, удовлетворяют условию прочности Мора-Кулона, то зависимости пр τi = f (σv) неинвариантны к виду напряженного состояния. Это положение подтверждается экспериментально (рис. 5, г). Данный вывод следует и из теоретических положений, представленных в [14, 29].
Связь между параметрами прочности по Мору-Кулону φм и См и Мизесу-Боткину φокт и Сокт при μσ = -1 определяется известными соотношениями
Сопоставим условие предельного состояния по Мору-Кулону и Мизесу-Боткину при μσ = 0.
Условие Мора-Кулона представим соотношением
σ1 – σ3 = (σ1 + σ3 + 2См ctg φм)·sin φм, (16)
а условие Мизеса-Боткина выражением
пр τi = (H + σv) tg φокт, (17)
которое представим в виде
(σ1 – σ2)2 + (σ2 – σ3)2 + (σ3 – σ1)2 = 2/3 [(σ1 + σ2 + σ3 + 3H) tg φокт2], (18)
где H = Cокт/tg φокт.
Используя условия:
σ2 = 0,5 (σ1 + σ3) и H = Cм/tg φм = Cокт/tg φокт,
и подставив их в равенства (16) и (18), получим соотношения,
tg φокт = sin φм; Сокт = См cos φм. (19)
Сопоставление условий предельного состояния по Мору-Кулону и Мизесу-Боткину при μσ = 1, используя условия:
σ1 = σ2 = 0, σ3 < 0, или σ1 = σ2 > σ3 (20)
приводит к соотношениям
![]() (21)
(21)
На рис. 5, г нанесены зависимости пр τi = f (σv), построенные по параметрам tg φокт и Сокт, определенным по формулам (15) и (19) при φм = 27°30' и См = 0,4 МПа. Сопоставление показывает, что они достаточно близки к зависимостям, полученным в экспериментах.
Используя условие, что экспериментальные данные, полученные при различных значениях параметра μσ, удовлетворяют критерию, прочности Мора-Кулона, переход от τiпр (μσ = -1) к τiпр (μσ = 0) при заданной величине среднего нормального напряжения может быть выполнен через коэффициент.
Составим равенство:
пр τ0i = K' пр τ-1i (22)
где пр τ0i и пр τ-1i - предельное значение интенсивности касательных напряжений при μσ = 0 и μσ = -1 соответственно; K' - переходный коэффициент.
Подставив в равенство (22) соответствующие выражения (15) и (19) для tg φокт и Сокт при μσ = 0 и μσ = -1, получим:
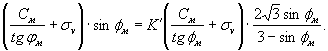 (23)
(23)
Упростив выражение (23), получим следующую формулу для переходного коэффициента:
![]() (24)
(24)
Анализ выражения (24) показывает, что величина К' зависит только от параметра φм, и его значение находится в пределах 0,866 > К' ≥ 0,578. Так, для φм = 27°30' коэффициент К' = 0,73.
На рис. 5, г нанесена зависимость пр τ°i, = f (σv), построенная по формуле (19), используя данные стабилометрических опытов. В табл. 2 даны параметры φокт и Сокт, а также предельные значения пр τi для различных величин среднего нормального напряжения.
Таблица 2
Параметры прочности φокт и Сокт
|
Метод испытания |
φокт |
Сокт |
Предельные значения пр τi, |
||||
|
σv = 0,2 МПа |
σv = 0,4 МПа |
σv = 0,6 МПа |
σv = 0,8 МПа |
||||
|
MKH μσ = 0 |
опытные данные по формуле (19) по стабилометру, по формуле (22) |
26°50' 24°40' 23° |
0,375 0,356 0,384 |
0,480 0,448 0,469 |
0,555 0,545 0,554 |
0,680 0,640 0,639 |
0,783 0,735 0,724 |
|
Стабилометр |
опытные данные по формуле (15) |
30°20' 32°30' |
0,523 0,500 |
0,640 0,627 |
0,757 0,755 |
0,874 0,882 |
0,991 1,080 |
Сопоставление результатов расчета с опытными данными на рис. 5, г и в табл. 2 показывает их достаточно близкое соответствие. Отличие в величинах пр τi, полученных экспериментально и расчетом, не превышает 10 %.
При сопоставлении зависимостей γi∞ = f (τi; σv) и МКН (рис. 5, б) с целью учета вида напряженного состояния в результате опытов, полученных при μσ = -1, введен корректировочный коэффициент К' = 0,73. Таким образом, сделано допущение, что влияние вида напряженного состояния на зависимости γi∞ = f (τi; σv) остается постоянным в допредельном и предельном состояниях. Данное допущение для исследованного материала достаточно хорошо подтверждается результатами экспериментов (рис. 5, б).
Используя подход, изложенный выше, переход от τiпр (μσ = 0) к τiпр (μσ = 1) при заданной величине среднего нормального напряжения выполняется по зависимости
пр τi0 = K'' пр τi1, (25)
где пр τi1 - предельное значение интенсивности касательных напряжений при μσ = 1; К" - переходный коэффициент.
Подставив в (25) соответствующие выражения tg φокт и Сокт из (19) и (21), получим формулу
![]() (26)
(26)
Анализ выражения (26) показывает, что коэффициент К" зависит только от параметра φм, и его значение находится в пределах 1,5 > К" ≥ 0,867.
Таким образом, величина К" в зависимости от φм может быть как больше, так и меньше единицы. Так, для φм = 27°30' коэффициент К" = 1.
На рис. 5, в представлены зависимости изменения деформации объема εDv∞ = f (τi, σv) на участке девиаторного нагружения (действие кольцевой касательной нагрузки). Анализ этих результатов показывает, что зависимости, полученные в стабилометре и МКН, практически совпадают.
Изложенные выше положения следует учитывать при сопоставлении результатов, полученных различными методами.
Общий анализ результатов экспериментов позволяет сделать вывод, что использование МКН дает возможность с достаточной для инженерных расчетов точностью определять параметры деформируемости и прочности полускальных и скальных грунтов. По сравнению с результатами испытаний в стабилометре, при определении зависимостей (1) ÷ (4) МКН возможная погрешность не превышает 10 ÷ 15 %.
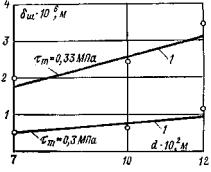
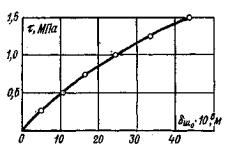
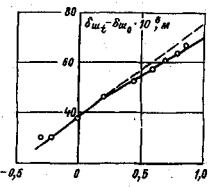
На рис. 6, 7 представлены результаты опытов, выполненных МКН при различных размерах кольцевой нагрузки, приложенной к поверхности исследуемого массива. Анализ результатов этих опытов показывает, что зависимости δш∞ = f (τd) с достаточной для практических целей точностью могут быть приняты линейными. Таким образом, экспериментально подтверждено одно из основных положений, использованных в МКН: в том случае, если соблюдены критерии квазиоднородности, то размер испытаний не оказывает влияния на определяемые параметры.
Физико-механические свойства исследованных грунтов
|
Тип грунта |
Плотность частиц ρS , |
Плотность грунта, ρ, |
Влажность W, % |
Коэффициент пористости е |
Прочность на сжатие пр σс°, МПа |
Прочность на растяжение, пр σp°, МПа |
|
Аргиллит |
2,70 |
2,17 |
1,20 |
0,26 |
14,60 |
1,06* |
|
Мергель в оттаявшем состоянии |
2,72 |
2,25 |
1,43 |
0,23 |
2,44* |
0,45* |
|
Известняк |
2,70 |
2,44 |
0,20 |
0,13 |
21,25 |
2,00* |
|
Туф |
2,66 |
1,84 |
0,30 |
0,45 |
14,54 |
1,93 |
|
Гипс (эквивалентный материал) |
2,06 |
0,84 |
11,0 |
1,73 |
1,25 |
0,25 |
* Значения пр σс° и пр σp определены на образцах малых размеров на приборе - пробнике БУ-39 по методике ВНИМИ.
Для изучения закономерностей деформируемости и прочности полускальных грунтов различных генетических типов в условиях пространственного напряженного состояния методом кольцевого нагружения на кафедре Механики грунтов, оснований и фундаментов МИСИ был выполнен большой объем экспериментальных исследований. Результаты данных опытов обработаны по представленной выше методике.
|
|
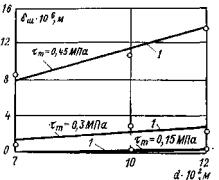
|
|
Рис. 6. Зависимость δш = f (τ, d) при σс = 0,1 Мпа 1 - по аналитическому решению; О - экспериментальные данные. |
Рис. 7. Зависимость δш = f (τ, d) при σс = 0,6 МПа 1 - по аналитическому решению; О - экспериментальные данные. |
Экспериментальные исследования полускальных грунтов МКН выполнены в немерзлом состоянии, а для мерзлых грунтов после их оттаивания [56].
Опыты проводились по программам, указанным на рис. 3.
Физико-механические свойства исследованных грунтов представлены в табл. 3.
Анализ результатов экспериментов позволил установить достаточно общие закономерности деформирования при пространственном напряженном состоянии грунтов и показал их практически полное соответствие тем закономерностям, которые были установлены при испытании эквивалентного материала.
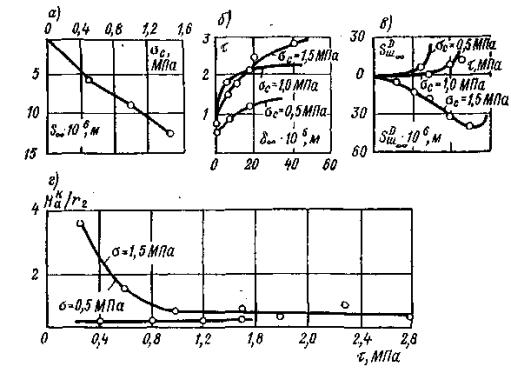
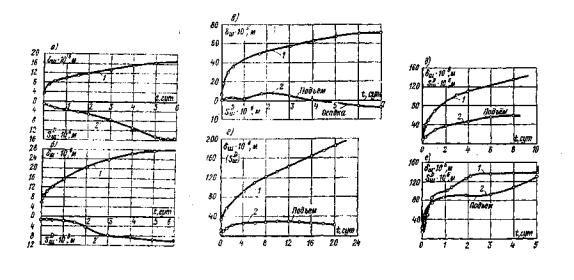
В качестве примера на рис. 8, а приведена характерная диаграмма зависимости осадок поверхности массива S∞ от величины среднего нормального напряжения на контакте целика c основанием из известняка. Как видно из рис. 8, а и из анализа результатов исследований других типов пород, данных зависимости имеют близкий к линейному характер, что подтверждает корректность предпосылки, принятой в методике при определении вида зависимости (I).
Рис. 8. Результаты испытаний методом кольцевого нагружения по зависимостям (порода - известняк):
![]()
В табл. 4 представлены результаты обработки опытных данных по формулам (7), (8) и (14).
Таблица 4
|
Тип грунта |
Модуль общей деформации Ec∞, МПа |
Коэффициент относительной поперечной деформации v |
Модуль объемной деформации Ev∞, МПа |
Аргиллит |
180 |
- |
- |
|
Мергель |
737 |
0,128 |
820 |
|
Известняк |
6447 |
0,07 |
7500 |
|
Туф |
6497 |
0,36 |
2325 |
Гипс |
810 |
0,126 |
1065 |
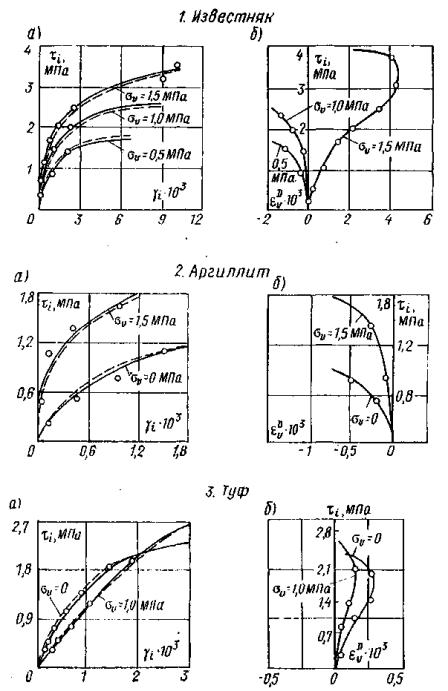
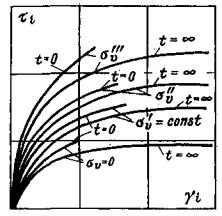
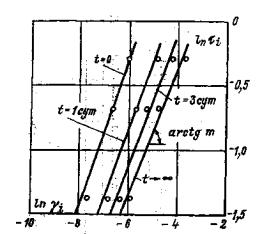
Рис. 9. Результаты испытаний методом кольцевого нагружения:
а) зависимость интенсивности деформаций сдвига от интенсивности касательных напряжений и среднего нормального напряжения γi = f (τ, σv);
б) зависимость относительных объемных деформаций от интенсивности
касательных напряжений и среднего нормального напряжения εDv = f (τ, σv).
Зависимости горизонтальных перемещений основания кольцевого целика от величины среднего касательного напряжения при различных нормальных напряжениях в опытах на монолитах известняка представлены на рис. 8, б. Анализ кривых δш∞ = f (τ, σ) показывает, что они имеют нелинейный характер и существенно зависят от величины нормального напряжения.
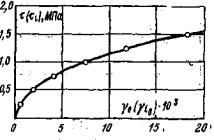
Зависимости интенсивности деформаций сдвига от интенсивности касательных напряжений, полученные в результате обработки данных опытов, представлены на рис. 9, а.
Диаграммы нелинейного деформирования исследованных грунтов достаточно хорошо аппроксимируются степенной зависимостью вида (пунктирные линии на рис. 9, а):
τi = A∞ γim, (27)
где A∞ - коэффициент деформирования, имеющий размерность напряжений (МПа); 0 < m ≤ 1-коэффициент упрочнения.
Значения параметров A∞ и m определяются путем решения системы двух уравнений методом наименьших квадратов:
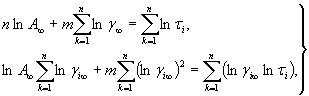 (28)
(28)
где n - число экспериментальных точек; - либо графически, на основе представления экспериментальных данных в логарифмических координатах (см. приложение 5).
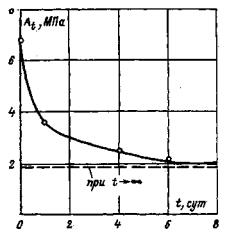
В табл. 5 даны параметры деформируемости A∞ и m, полученные в опытах при различных значениях среднего нормального напряжения σv для некоторых исследованных типов полускальных грунтов.
Таблица 5
Параметры деформируемости A∞ и m
|
Параметры деформи- |
Тип грунта |
||||||||
|
аргиллит |
туф |
мергель |
алевролит |
гипс |
|||||
|
Величина σv, МПа |
|||||||||
|
0 |
° |
1,0 |
0,75 |
1,2 |
0 |
0,4 |
0,6 |
0,8 |
|
|
A∞, Мпа |
58,3 |
645,7 |
296,8 |
8,03 |
13,54 |
1,85 |
2,32 |
2,68 |
3,31 |
|
m |
0,63 |
0,85 |
0,83 |
0,52 |
0,5 |
0,31 |
0,36 |
0,37 |
0,38 |
Во всех опытах касательные напряжения доводились до предельной величины пр τ, приводящей к разрушению. Разрушение происходило на участке контакта кольцевого целика и массива и во всех опытах имело близкий к плоскому кольцевой характер. На основе методики, изложенной в разделе 6, были определены в каждом опыте значения пр τ∞, соответствующие пределу длительной прочности. На основе повторных испытании сопротивляемости сдвигу грунтов по образовавшейся в результате первого опыта (разрушения) трещине определялась остаточная прочность на сдвиг τr. Испытания проводились при нескольких различных значениях нормального напряжения.
Для всех исследованных полускальных грунтов зависимости предельного и остаточного сопротивления сдвигу в осях пр τ∞ - σ и τr - σ имеют практически линейный характер. Параметры сопротивления сдвигу исследованных типов грунтов представлены в табл. 6.
Таблица 6
Параметры сопротивления сдвигу
|
Параметры сопротивления сдвигу |
Тип полускального грунта |
|||||
|
аргиллит |
мергель |
известняк |
туф |
алевролит |
гипс |
|
|
φ∞, град |
21 |
29 |
40 |
14 |
39 |
27,5 |
|
С∞, МПа |
0,75 |
0,6 |
2,0 |
2,25 |
1,15 |
0,4 |
|
φr град |
31 |
27 |
41 |
21 |
36,5 |
27 |
|
Сr, МПа |
0,15 |
0,23 |
0,2 |
0,5 |
0,09 |
0,1 |
Приложение 2
ИСПОЛЬЗОВАНИЕ МЕТОДОВ ИНЖЕНЕРНОЙ ГЕОФИЗИКИ
ДЛЯ ОЦЕНКИ РЕОЛОГИЧЕСКИХ СВОЙСТВ СКАЛЬНЫХ
И ПОЛУСКАЛЬНЫХ ГРУНТОВ В МАССИВЕ
В результате выполнения опытов МКН параметры реологических свойств скальных и полускальных грунтов устанавливаются только в отдельных (базовых) точках массива, вмещающего подземное сооружение. Кроме того, значительная часть геомеханических испытаний проводится на стадии инженерно-геологических изысканий, и во многих случаях на этой стадии не имеется возможности проводить крупномасштабные полевые опыты непосредственно в зонах расположения подземных сооружений, длина которых может достигать километров и десятков километров (туннель Арна-Севан - 48 км, напорный туннель ИнгуриГЭС - 16 км).
В данных условиях неизбежно встает вопрос о переносе результатов точечных статических испытаний на различные участки массива, вмещающего подземное сооружение, т.е. о разработке геомеханической модели массива. В практике гидротехнического строительства для решения данной задачи широко используются косвенные инженерно-геологические методы.
Одним из наиболее надежных и широко используемых в отечественной и зарубежной практике методов оценки механических свойств скальных и полускальных грунтов в массиве является сейсмоакустический метод [33, 40, 49]. Использование данного метода для оценки механических свойств грунтов основано на построении эмпирических корреляционных связей между скоростью распространения динамических колебаний в массиве или динамических характеристик среды, являющихся производными величинами от скорости, и параметрами механических свойств грунтов, определенными в результате статических методов испытаний.
Методические вопросы построения корреляционных связей и построения геомеханических моделей скальных и полускальных грунтов изложены в указанных выше работах. Вместе с тем, вопросы оценки реологических свойств скальных и полускальных грунтов в массиве в этих работах не нашли достаточного отражения.
Учитывая важное практическое значение решения данного вопроса, в настоящем разделе представлены полученные корреляционные связи между параметрами реологических свойств скальных и полускальных грунтов и их динамическими параметрами [23, 57].
При построении корреляционных связей сохранен общий подход, выработанный в практике гидротехнического строительства.
Следует отметить большие возможности и перспективность совместного использования методов инженерной геофизики и МКН при определении реологических свойств скальных и полускальных грунтов в массиве.
С целью установления корреляционных связей между параметрами реологических свойств полускальных грунтов и скоростью продольных ультразвуковых волн vp выполнены совместные статические опыты МКН и динамические экспериментальные исследования. Совместные статические и динамические исследования были выполнены на образцах и монолитах аргиллита, известняка, мергеля, туфа, песчаника, алевролита и гипса в естественном состоянии, а мергеля после его оттаивания. Минимальные размеры исследуемых монолитов 30×30×30 см, максимальные - 50×50×50 см. По стандартным методикам для исследованных грунтов определены физико-механические свойства и скорость продольных упругих волн (табл. 1). Ультразвуковые измерения выполнялись на приборе УКБ-1М, собственная частота излучателя 100 кГц. Измерялись скорости продольных vp и поверхностных vR волн по методике прозвучивания в 3-х взаимно перпендикулярных направлениях до начала опыта и в процессе проведения опытов МКН. Обобщались данные серий измерений и проводилась их статистическая обработка.
Таблица 1
Физико-механические свойства полускальных грунтов
|
Тип грунта |
Плотность ρ, г/см3 |
Плотность частиц ρS, |
Влажность естественная W |
Коэффициент пористости |
vρ, км/с |
|
Аргиллит |
2.08-2,17 |
2,60-2,71 |
0,013 |
0,26-0,27 |
1.8-2,19 |
|
Известняк |
2,20-2,44 |
2,70 |
0,0022 |
0,13-0,23 |
3,10-3,30 |
|
Мергель |
2,25 |
2,72 |
0,0143 |
0,23 |
1,5-2,3 |
|
Туф |
1,48-1,84 |
2,54-2,66 |
0,003-0,0077 |
0,45-0,73 |
1,91-2,44 |
|
Гипс |
0,72-1,10 |
1,68-1,91 |
0,1-0,267 |
1,13-2,25 |
1,85-2,36 |
В результате проведенных опытов установлены достаточно тесные корреляционные зависимости вида ρ = avp + b между скоростью предельных волн vp и плотностью грунта ρ, а также между vp и коэффициентом пористости для грунтов, находящихся практически в воздушно-сухом состоянии. Линейные уравнения, отражающие эти связи, представлены в табл. 2. Коэффициент корреляции полученных соотношений близок к 1.
Таблица 2
Корреляционные уравнения связи скорости продольных волн vp с плотностью ρ и коэффициентом пористости е грунтов
|
Тип грунта |
Уравнение связи плотности ρ, г/см3 и скорости упругих волн vp. км/с |
Уравнение связи коэффициента пористости е и скорости упругих волн vp км/с |
|
Аргиллит |
ρ = 0,8 vp + 0,40 |
е = 0,5 – 0,1 vp |
|
Известняк |
ρ = 1,2 vp – 1,5 |
е = 1,8 – 0,5 vp |
|
Мергель |
ρ = 0,8 vp + 0,5 |
- |
|
Туф |
ρ = 0,64 vp + 0,2 |
е =1,8 – 0,54 vp |
|
Гипс |
ρ = 0,7 vp – 0,6 |
е = 6,3 – 2,2 vp |
Построение корреляционных связей между параметрами реологических свойств исследованных типов грунтов и скоростями упругих волн основывалось на следующих положениях:
- корреляционные связи устанавливались между скоростью распространения предельной упругой волны vp и параметрами реологических свойств грунтов, полученными на начальных этапах нагружения массива кольцевой нормальной и касательной нагрузками, где операторы Ect и Gt линейно зависят от напряжения и времени;
- ядро ползучести оператора Ect принято в виде (11, раздел 6), а ядро ползучести оператора Gt - в виде (19, раздел 6);
- используется двойная корреляция, на первом этапе устанавливаются зависимости между параметрами Ес0; G0; Еc∞; G∞ и скоростью vp, а на следующем этапе корреляционные зависимости между параметрами Ес0; G0; Еc∞; G∞ и параметрами ползучести θПσ; Tσ; θПτ; Tτ;
- в связи с тем, что в результате анализа опытных данных было выявлено отсутствие корреляции между параметрами λσ и λτ и другими показателями реологических свойств исследованных грунтов, их значении приняты постоянными λσ = λτ = 60 сут-1, оценка данного допущения показала, что оно не вносит существенной погрешности при практической реализации полученных корреляционных связей;
- полученные соотношения корреляционных связей могут рассматриваться как надежные в интервалах действия σс до 2 ÷ 4 МПа и пределах изменения Ec∞ от 100 до 7000 МПа, а τ до 2 МПа и G∞ от 50 до 1500 МПа, т.е. в исследованных пределах.
Установлено, что корреляционные зависимости между скоростями продольных волн vp и модулями деформации Ес0 и Ес∞ при сжатии и сдвиге G0 и G∞ достаточно устойчивые. Для всех исследованных типов грунтов обобщенные линии регрессии задавались в виде степенных функций
у = ахb (1)
где а и b - коэффициенты.
Полученные в результате обработки слитых данных уравнения регрессии имеют вид:
vp = 0,74 E0,15c, (2)
vp = E0,12c∞, (3)
vp = 0,5 G0,210, (4)
vp = 0,95 G0,15∞. (5)
Размерность vp - км/с; Ec0, Ec∞, G0, G∞ - МПа.
Для оценки параметров реологических свойств по значениям скоростей упругих волн практический интерес представляют уравнения обратной регрессии:
Ec0 = 71,7 v4,0p, (6)
Ec∞ = 11,5 v5,2p, (7)
G0 = 25,7 v2,0p, (8)
G∞ = 21,4 v3,6p, (9)
Известно, что скорость продольных волн vp зависит от плотности и влажности грунтов. Вычисляя корреляционные зависимости между vp и реологическими параметрами, приходится полагать постоянными показатели физических свойств и состояния (плотность, влажность и т.п.). Однако, если известны закономерности связей vp с этими показателями, то их влияние можно исключить или «исправить» значения vp. Примером такого преобразования может служить уравнение (7). Учитывая полученную при измерениях на образцах зависимость плотности ρ от скорости продольных волн vp (табл. 2) вводим уравнение ρ = f (vp) в выражение (7). Таким образом, получаем «исправленные» значения vp для каждого грунта, приводя все значения к плотности ρ, например, к плотности известняка, после чего снова вычисляем корреляционную зависимость. Новое уравнение регрессии имеет вид:
vp = 1,3 E0,1c∞. (10)
При этом корреляционное отношение повысилось с η1 = 0,75 для выражения (7) до η2 = 0,95 для (10). Четкая корреляция установлена между параметрами ползучести Тσ и θσ и параметрами Ec0 и Ec∞.
Tσ = 1053Ec0-1,05, (11)
θσ = 55160 Ec0-1,11, (12)
Tσ = 118 Ec∞-0,85, (13)
θПσ = 9969 Ec∞-0,96. (14)
Размерность Tσ - сут; θПσ – 10-5 МПа-1.
Анализ опытных данных показал, что четкие корреляционные связи между параметрами ползучести θПτ, Tτ и параметрами G0 и G∞ для исследованной совокупности грунтов не выявляются. Формально вычисленные уравнения регрессии имеют вид:
Tτ = 1,2 G0-0,11, (15)
Tτ = 0,56 G∞-0,01, (16)
θПτ = 49,5 G0-0,24, (17)
θПτ = 26,9 G∞-0,13. (18)
В уравнении (18) связь более четкая, чем в трех предыдущих.
Сейсмоакустический метод эффективно используется и при оценке параметров прочности образцов скальных и полускальных грунтов. Ф.М. Ляховицким [28] получена и широко используется на практике формула, выражающая линейную связь между пределом прочности на одноосное сжатие и величиной ρv2p. Коэффициент пропорциональности данной зависимости устанавливается эмпирическим путем для каждого типа грунта. Ввиду того, что диапазон значений vp в любом опыте ограничен снизу и, естественно, не включает значения коэффициента пропорциональности, близкие к нулю, предлагаемая вышеупомянутой формулой связь пр σc = 0, если ρv2p = 0, слишком жестко ограничивает выбор соответствующей опыту линии регрессии и тем ухудшает точность описания реально наблюдаемых взаимосвязей. Поэтому при анализе полученных опытных данных, исследуя связь с ρv2p, взято за основу равенство, которое можно считать некоторым обобщением формулы Ф.М. Ляховицкого:
пр σ0c = a ρ v2p + b.
Результаты расчета доказали большую достоверность: уравнения по сравнению с известной формулой, что выражается существенным повышением тесноты корреляционных связей, Близкий подход принят в работе [60] для аналогичных по типу полускальных грунтов. Более того, при сравнении данных экспериментов, проведенных нами и представленных в упомянутой работе, выявилась их достаточно хорошая взаимосогласованность, позволившая объединить все результаты опытов в единую статистическую совокупность (табл. 3).
Таблица 3
Связь между прочностью на одноосное сжатие пр σ0c (МПа) и скоростью распространения продольных волн vp (км/с)
|
Тип грунта |
Уравнение связи |
|
Аргиллит (влажный) |
пр σ0c = 1,7ρ·v2p – 12,0 |
|
Туфобрекчия (влажная) |
пр σ0c = 1,6ρ·v2p – 10,9 |
|
Выветрелый андезит |
пр σ0c = 1,2ρ·v2p – 4,6 |
|
Вулканическая брекчия |
пр σ0c = 0,5ρ·v2p + 2,2 |
|
Туф* |
пр σ0c = 2,5ρ·v2p – 2,2 |
|
Гипс* |
пр σ0c = 1,6ρ·v2p – 0,8 |
* Опыты МИСИ.
Приведенные в табл. 3 уравнения позволяют достаточно надежно определять величину пр σ0c различных типов полускальных грунтов по сейсмоакустическим данным.
При исследовании монолитов полускальных грунтов МКН получены параметры их сопротивления сдвигу – сцепление См и угол внутреннего трения φм. Предварительный анализ показал отсутствие прямой корреляционной связи между этими параметрами и скоростями продольных упругих, волн. В связи с этим был предложен способ косвенной корреляции. Исходя из допущения применимости теории прочности Мора-Кулона (см. приложение 1), по полученным экспериментальным путем значениям См и φм можно определить прочность на одноосное сжатие грунта в массиве по формуле
![]() (19)
(19)
Вычисленные значения пр σсм по экспериментальна полученным параметрам использовались при установлении корреляционных зависимостей со скоростью прохождения продольных ультразвуковых волн в массиве vр. При этом была обобщена вся совокупность исследованных типов грунтов. Кривые регрессии имеют вид:
vp = 0,27пр σс0м + 0,64, (20)
vp = 0,24пр σс∞м + 1,33, (21)
где пр σс0м - значение условно-мгновенной прочности на одноосное сжатие, соответствующее параметрам См0 и φм0 в массиве; σс∞м - предел длительной прочности, соответствующий параметрам См∞ и φм∞.
Анализ полученных зависимостей указывает на достаточно, тесную корреляционную связь между пр σсм и vp, с помощью которой по значениям vp можно оценить прочность пород на одноосное сжатие в массиве. Кроме того, можно оценить параметры См0, φм0 и См∞ и φм∞ для различных моментов времени, применяя следующий подход, основанный на совместном использовании статических и динамических испытаний. По результатам статических испытаний МКН при приложении к массиву только кольцевой касательной нагрузки, без вертикального нагружения, определяется величина сцепления См0 или См∞, а по результатам ультразвукового прозвучивания - величина vp. Используя уравнения связи (20) и (21), оценивается величина пр σсм и, используя формулу (19), определяются параметры φм0 или φм∞:
ctg (φм0/2) = 2C м0 пр σс0м, (22)
ctg (φм∞/2) = 2C м∞ пр σс∞м (23)
Данный подход позволяет значительно упростить статические исследования с использованием МКН, так как появляется возможность сократить количество опытов по прямому определению параметров предельного сопротивления сдвигу полускальных грунтов при различных нормальных напряжениях.
Отметим, что при установлении корреляционных связей необходимо учитывать влияние дополнительных факторов, таких как влажность и плотность полускальных грунтов в условиях естественного залегания. Эти факторы оказывают очень большое влияние на реологические свойства полускальных грунтов.
Построение корреляционных связей между параметрами ползучести скальных грунтов при сжатии и скоростью прохождения продольных ультразвуковых волн в массиве
С целью построения корреляционных связей между параметрами ползучести при сжатии и скоростью прохождения продольных ультразвуковых волн использованы результаты длительных толевых штамповых опытов, выполненных на различных гидротехнических объектах [57]. Параметры ползучести и средние скорости упругих волн в массиве представлены в табл. 4.
При проведении штамповых опытов скальные грунты находились в водонасыщенном состоянии.
В соответствии с исходными данными (табл. 4) построены корреляционные зависимости между параметрами Ес0, Ес∞ и скоростями продольных ультразвуковых волн в массиве vp:
Таблица 4
Параметры ползучести и скорости продольных упругих волн vp в массиве по результатам полевых исследований
|
Гидроузел |
Тип грунта, |
Расчетный интервал
Δσс, |
Ес0·10-4, МПа |
Ес∞·10-4, МПа |
θσ·10-4, Мпа-1 |
Tσ, сут |
vp, км/с |
|
Андижанский |
Метаморфические сланцы черные № 22 |
0-4,0 |
1,4 |
0,51 |
0,82 |
0,22 |
4,8* |
|
Фархадский |
Микросланцы № 3 |
1,0-2,0 |
1,34 |
0,38 |
0,58 |
0,26 |
5,7* |
|
№ 4 |
1,0-2,0 |
0,65 |
0,42 |
0,29 |
0,31 |
5,6* |
|
|
Кировский |
Хлоритосерицитовые сланцы № з |
1,0-4,0 |
0,57 |
0,27 |
1,63 |
0,27 |
5,3* |
|
№ 4 |
1,0-4.0 |
0,64 |
0,37 |
0,64 |
0,18 |
5,3* |
|
|
Слоистые песчаники № 7 |
1,0-4,0 |
1,65 |
0,83 |
0,17 |
0,07 |
5,8* |
|
|
Ингурский |
Известняки доло- |
0-8,0 |
0,47 |
0,39 |
0,20 |
0,21 |
- |
|
Средней сохранности № 1 |
4,0-7,0 |
0,26 |
0,11 |
4,95 |
0,419 |
3,8** |
|
|
№ 4 |
6,0-7,0 |
0,23 |
0,052 |
4,93 |
0,612 |
- |
|
|
№ 5 |
6,0-10,0 |
0,37 |
0,115 |
3,8 |
0,37 |
4,0** |
|
|
Сильно раздроб- |
2,0-4,0 |
0,068 |
0,029 |
12,13 |
0,34 |
1,5* |
* По данным С.Б. Ухова и А.С. Паненкова [49].
** По данным А.И. Савича.
Ес0 = 284 vp2,06 (24)
Ес∞ = 106 vp2,15 (25)
Корреляционные связи между параметрами ползучести θσ, Tσ и параметрами Ес0 и Ес∞ получены в виде следующих уравнений:
Tσ = 6,6 E-0,38с0, (26)
θПσ = 4,5 E-1,24с0, (26)
Tσ = 5,7 E-0,4с∞, (27)
θПσ = 2,2 E-1,28с∞. (28)
Параметр λσ принят постоянным для всех грунтов λσ = const = 100 сут-1, что не вносит существенной погрешности при практической реализации полученных корреляционных, связей
Графическое представление полученных корреляционных связей представлено на рис. 1.
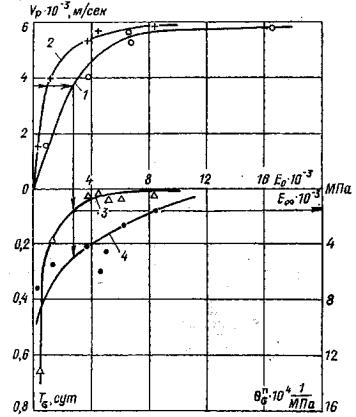
Рис. 1. Корреляционные зависимости параметров ползучести скальных грунтов от средней скорости распространения продольных ультразвуковых волн в массиве
1 - Ес0 = f (Vp); 2 - Ес∞ = f (Vp); 3 - θПσ = f (Ес∞); 4 - Tσ = f (Ес∞).
Приложение 3
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
И ТЕХНОЛОГИИ ПОДГОТОВКИ ОПЫТОВ
Принципиальная схема стенда для проведения испытаний монолитов породы размером в плане 0,5×0,5 м представлена на: [56]*.
* Чертежи лабораторной установки можно получить в ОНИЛИМЭС СИ. Конструкция установки разработана В.Л. Кубецким и В.А. Козиоым.
На станине 1 установлен секционный лоток 2, в который помещается исследуемый монолит породы 3. Жесткое закрепление монолита в лотке достигается путем его погружения в бетонную оболочку 4. Кольцевой целик породы 5, неразрывно связанный с основанием (монолитом), имеет следующие размеры: внутренний диаметр 60 мм; наружный диаметр 100 мм; высоту 30 мм. На кольцевой целик одевается металлический захват с кольцевой полостью 6.
Рис. 1. Принципиальная схема стенда.
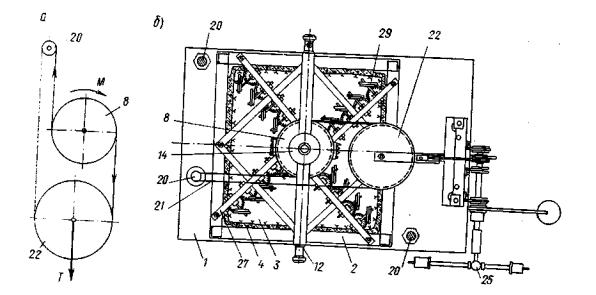
Рис. 2. Принципиальная схема стенда:
а) схема приложения крутящего момента; б) вид в плане.
Приложение нормального давления к основанию через кольцевой целик осуществляется при помощи рычажной системы, включающей рычаг 13 и нагрузочную раму 12. Величина максимального усилия, создаваемого рычажной системой, составляет, 100 Н. Для увеличения вертикального усилия на основание может быть использована гидравлическая система, включающая цилиндр давления 30, стабилизатор давления 31 камеру давления 15, расположенную в верхней части нагрузочного цилиндра 14. Контроль за величиной давления жидкости в гидравлической системе осуществляется при помощи манометра 32. Для обеспечения равномерной подачи нагрузки на основание крышка камеры давления 16 через переходник 17 шарнирно соединена отцентрированным относительно целика винтом 18 упорной рамы 19. Величина максимального вертикального усилия, передаваемого на основание с использованием гидравлической системы, составляет 20,0 кН.
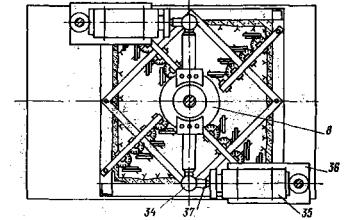
Рис. 3. Принципиальная схема стенда с применением гидродомкратов (вид в плане).
Приложение горизонтального усилия осуществляется при помощи рычага 25 с соотношением плеч 1 : 15, установленного на стойках 20. Усилие от рычага передается через скобу 24 на распределительный диск 22, который при помощи троса 21, огибающего стойку 20, и осуществляет приложение крутящего момента к диску 8 (рис. 2). Создаваемый механизмом кручения момент передается целику породы через переходной цилиндр 7. Упорный подшипник 9 обеспечивает независимость приложения вертикальных и горизонтальных усилий.
Нагрузочные системы стенда обеспечивают создание на подошве кольцевого целика принятых размеров нормальных напряжений до 5,0 МПа и касательных напряжений до 4,0 МПа. При необходимости стенд оборудуется двумя горизонтальными гидравлическими домкратами, которые позволяют увеличить касательное напряжение до 15 МПа (рис. 3). Для этой цели к диску кручения 8 жестко прикрепляется консоль 33, имеющая на конце сферический шарнир. Гидравлические домкраты 34 грузоподъемностью до 500 Н, устанавливаемые на пластине 35 при помощи скоб 36, через шарнир 37. осуществляют приложение к основанию через кольцевой целик касательной нагрузки.
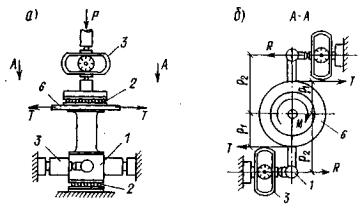
Рис. 4. Схема тарировки стенда:
а) нормальной нагрузки; б) горизонтальной нагрузки.
Измерение перемещений целика и окружающей его поверхности породы выполняется индикаторами часового типа 29 с точностью до 1·10-6 м по реперам 26, расположенным на различном расстоянии от оси целика по четырем взаимноперпендикулярным створам.
Стенд имеет следующие технические характеристики: размеры лотка - 0,55×0,55×0,40 м; величина максимального вертикального усилия - 30,0 кН; величина максимального крутящего момента - 3,0 кНм; площадь поперечного сечения основания кольцевого целика - 5×10-3 ÷ 10×10-3 м2; точность измерения вертикальных и горизонтальных перемещений - 1×10-6 м; габаритные размеры установки 0,7×1,5×2,3 м.
Определение усилий, передаваемых к основанию через кольцевой целик от нагрузочных систем стенда, выполняется по результатам тарировочных испытаний. Принципиальная схема тарировки стенда представлена на рис. 4. При тарировании нагрузочных систем стенда на вертикальные усилия по динамометру 3 определяется значение нагрузки, создаваемое рычагом 13 и гидравлической камерой 15 (рис. 5). Пользуясь тарировочными графиками, представленными на рис. 5, а, б, в, определяем усилие, передаваемое на основание при заданном значении веса груза на подвеске рычага Q и заданном давлении в гидравлической камере Р0, которое определяется по показаниям манометра 32 (рис. 4). По найденному значению вертикального усилия P определяется среднее значение нормального напряжений a подошве кольцевого целика
![]() (1)
(1)
где r1 и r2 - соответственно внутренний и наружный радиусы: кольцевого целика; N - вес системы приложения вертикальной нагрузки.
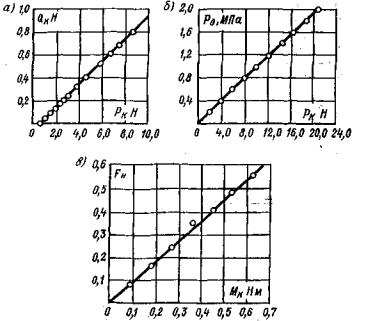
Рис. 5. Тарировочные графики:
а) вертикальная рычажная система; б) гидравлическая камера; в) горизонтальная рычажная система.
Тарировка горизонтальной
нагрузки (крутящего момента) выполняется по схеме (рис. 4, б). Данная схема
проведения тарировочных испытаний обеспечивает возможность определения личины
крутящего момента на участке непосредственного ![]() приложения к кольцевому целику.
приложения к кольцевому целику.
Горизонтальное усилие Т, создаваемое нагрузочной системой стенда, передается от диска кручения 6 к тарировочной балке 1, которая шарнирно соединена с двумя динамометрами 3. При известных геометрических размерах ρ1 и ρ2 по показаниям динамометров R устанавливается значение величины крутящего момента М, передаваемого к кольцевому целику. Для учета влияния сил трения, возникающих в упорных подшипниках 2, тарирование выполняется при различных значениях нормального усилия σ.
Используя тарировочный график (рис. 5, в), определяем величину М при заданной величине угла веса груза F на подвеске горизонтального рычага.
Среднее касательное напряжение на подошве кольцевого целика τср определяется по зависимости
![]() (2)
(2)
где ξ = r1/r2.
При выводе зависимости (2) принята трапецеидальная эпюра распределения касательных напряжений τ на участке сопряжений кольцевого целика и основания.
Для проведения испытаний проба исследуемой породы отбирается в виде монолита ненарушенного состояния. Монолит породы может иметь достаточно произвольную форму и размеры, определяемые, главным образом, его транспортабельностью.
При отборе проб необходимо соблюдение мер по обеспечению полной сохранности их естественного состояния и влажности. Для слабых скальных и полускальных грунтов вырезку монолитных проб рекомендуется производить при помощи цепной пилы МС-10, выпускаемой опытно-экспериментальным заводом ВНИМИ. Для слабых разновидностей полускальных пород приемлемы методы, используемые при отборе проб грунтов.
Отделенный от основного массива монолит породы парафинируется и упаковывается с указанием его ориентации, даты и места отбора.
Подготовка монолита породы к проведению испытаний осуществляется в лабораторных условиях. Первоначально выполняется визуальная оценка состояния пробы, заключающаяся в установлении степени ее сохранности, характера трещиноватости и других особенностей строения. Результаты осмотра документируются в виде фотографических снимков и масштабных зарисовок состава и строения породы. Наряду с визуальным осмотром выполняется сквозное ультразвуковое прозвучивание монолита по трем взаимноперпендикулярным направлениям. По результатам прозвучивания определяется скорость прохождения упругих волн и устанавливается степень однородности породы в пределах исследуемого объема. Для определения показателей физических свойств выполняется отбор проб в процессе подготовки кольцевого целика.
Для обеспечения неизменности исходных физико-механических свойств породы в ходе опыта внешняя поверхность; монолита покрывается тонким слоем эпоксидного клея. После того как клей затвердеет, выполняется операция по подготовке кольцевого целика. Кольцевой целик с заданными внутренними внешним диаметрами изготавливается при помощи специальной кольцевой буровой коронки, либо обуриванием по периметру скважинами малого диаметра с последующим разбором окружающей его поверхности породы. Общий вид подготовленного к испытанию монолита породы с кольцевым целиком, представлен на рис. 6. Подготовленный к испытанию монолит устанавливается в лотке стенда. Жесткое закрепление монолита осуществляется путем погружения его в бетонную смесь. На целик одевается металлический захват с кольцевой полостью (рис. 7). Жесткая связь кольца и целика породы обеспечивается эпоксидным клеем.
|
|
|
|
Рис. 6. Вид подготовленного к испытанию монолита грунта с кольцевым целиком 1 - кольцевой целик; 2 - исследуемый массив. |
Рис. 7. Общий вид кольцевого целика с установленным металлическим захватом 1 - исследуемый массив; 2 - металлический захват. |
В тех случаях, когда подготовить кольцевой целик не представляется возможным из-за сильной трещиноватости породы, нагружение монолита осуществляется кольцевым бетонным штампом [24].
Технология подготовки опытов с использованием бетонных штампов существенно упрощается. Рабочая поверхность предназначенного для опытов монолита породы предварительно выравнивается. Для лучшего сцепления штампа с породой поверхность породы может иметь неровности до 5 мм, что в некоторой степени моделирует условия испытаний в полевых опытах.
На подготовленной поверхности монолита устанавливается опалубка и бетонируется армированный штамп, имеющий в плане кольцевую площадь примыкания к породе. Элементами штампа являются (рис. 8) внешняя 2 и съёмная 3 опалубки, крестовина 4, арматура 5, крепежные болты 8 и заполняющий бетон цементный раствор 6. Изготовление штампа производятся в следующей последовательности.
Собирается каркас штампа, для чего устанавливается арматура 6, скрепляющаяся в центре замковым соединением. К арматуре крепится с помощью болтов внешняя опалубка 3, состоящая из 4-х секторов. К опалубке крепежными болтами 8 присоединяется крестовина 4, служащая для передачи крутящего момента. Для предотвращения контакта металлической опалубки с породой нижняя часть опалубки выполняется съемной, состоящей из 2-х частей. Съемная опалубка устанавливается непосредственно на поверхность монолита. Для получения кольцевой в плане площади контакта штампа с породой в центральной полости кольца устанавливается круглая пластина из пенопласта (d = 3 мм) со слоем изоляционного покрытия. Собранный каркас штампа устанавливается на съемную опалубку, затем конструкция заполняется цементным раствором. Одновременно с бетонированием штампа производится заполнение цементным раствором форм для изготовления образцов-балок 40×40×160 мм. Для изготовления цементного раствора рекомендуется использовать цемент марки В40. После набора бетоном прочности съемная опалубка удаляется.
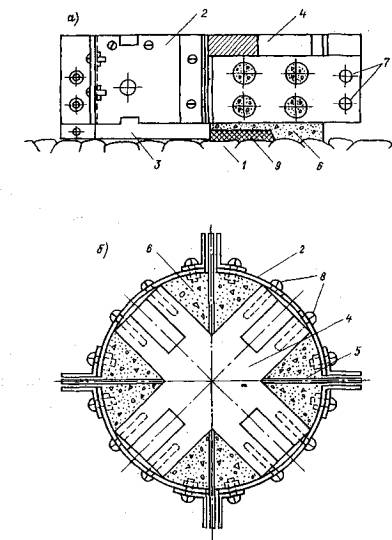
Рис. 8. Сборочный чертеж бетонного штампа:
а) вид сбоку; б) вид сверху:
1 - поверхность грунта; 2 - внешняя опалубка; 3 - съемная опалубка; 4 - крестовина; 5 - арматура; 6 - бетон; 7 - проушины; 8 - крепежные болты; 9 - низкомодульная прокладка.
Растягивающее усилие передается на штамп через арматуру 5 и внешнюю опалубку 2. При этом штамп соединен с нагрузочной системой через специальные проушины в арматуре к внешней опалубке. Сжимающее усилие и крутящий момент передаются на подошву штампа через крестовину 4 и внешнюю опалубку 2, соединенную с крестовиной крепежными болтами, а также арматуру 5, работающую совместно с внешней опалубкой.
В специальных прорезях штампа и на поверхности основания вокруг кольцевого штампа устанавливаются реперы для замера перемещений штампа и породы в процессе испытаний. Для предотвращения изменения свойств породы в процессе испытаний рабочая поверхность монолита парафинируется или покрывается защитной эпоксидной пленкой.
Подготовленный к испытаниям монолит породы с прибетонированным штампом укрепляется в лотке, после чего лоток устанавливается на стенд.
После окончания процесса твердения бетона, окружающего монолит породы в лотке, выполняется монтаж нагрузочных систем стенда. Точность установки вертикальной нагрузочной системы контролируется по отвесу, а горизонтальной - по уровню.
На заключительном этапе подготовительных работ выполняется монтаж измерительной системы стенда. Вначале на кольцевом целике и окружающей его поверхности породы по определенной схеме (рис. 9) устанавливаются реперы. Закладка реперов в породу осуществляется при помощи эпоксидного клея в заранее пробуренные скважины глубиной 3-5 мм. При установке реперов необходимо, чтобы максимальный размер неровностей поверхности породы вокруг целика не превышал 10 мм. Индикаторы при помощи специальных держателей неподвижно закрепляются на жесткой измерительной раме (рис. 1).
При проведении испытаний особое внимание должно быть уделено мероприятиям, обеспечивающим заданный температурный режим в помещении, где проводятся исследования. Как показали специальные опыты, колебания температуры воздуха в пределах 2 ÷ 3°С для данной конструкции измерительной системы не приводят к изменению показаний индикаторов.
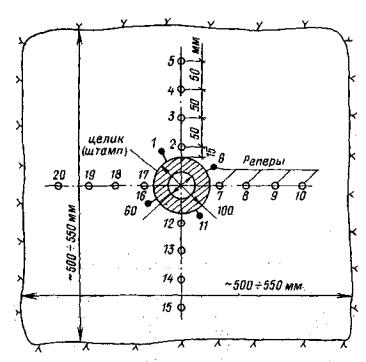
Рис. 9. Схема установки реперов
1, 2, 3 н т.д. - номера реперов.
Соблюдение указанных требований позволяет исключить влияние температуры на показания индикаторов при обработке экспериментальных исследований.
После проведения опыта по заданной программе и разрушения контакта целика или штампа с основанием выполняется разборка основания на глубину до одного радиуса кольцевого, целика. Как показали исследования, на одном монолите представляется возможным выполнить 3-4 опыта по различным программам нагружения.
Приложение 4
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ О РЕОЛОГИЧЕСКИХ СВОЙСТВАХ
ПОЛУСКАЛЬНЫХ ГРУНТОВ ПРИ РАЗЛИЧНЫХ НАПРЯЖЕННЫХ
СОСТОЯНИЯХ, ПОЛУЧЕННЫЕ МКН.
Таблица 1
Параметры ползучести
|
Тип грунта |
Известняк |
Туф |
Аргиллит* |
Мергель |
|
Параметры ползучести при сжатии |
||||
|
Расчетный интервал |
|
|
|
|
|
Δσс МПа |
0-2,5 |
1,0-2,0 |
1,0-2,0 |
0,25-1,25 |
|
Ес0, МПа |
5830 |
6350 |
580 |
857 |
|
Ес∞, МПа |
3290 |
2920 |
212 |
221 |
|
v0 |
0,22 |
0,22 |
- |
- |
|
v∞ |
0,25 |
0,40 |
- |
0,128 |
|
θПσ·105, МПа-1 |
4,9 |
9,3 |
34,9 |
62,4 |
|
λσ, сут-1 |
62.4 |
86,4 |
48,0 |
24,8 |
|
Тσ, сут |
0,46 |
0,22 |
1,24 |
4,34 |
|
Параметры ползучести при сдвиге вручением |
||||
|
Расчетный интервал |
|
|
|
|
|
Δτ, МПа |
0,25-1,25 |
0-1,5 |
0,25-0,75 |
0-0.25 |
|
σс, МПа |
0 |
0 |
0 |
0,75 |
|
G0 МПа |
2410 |
1710 |
1086 |
553 |
|
G∞, МПа |
1320 |
1154 |
492 |
865 |
|
θПτ·105, МПа-1 |
9,7 |
11,5 |
33,5 |
126 |
|
λτ, сут-1 |
60 |
38,4 |
36 |
19 |
|
Тτ, сут |
0,39 |
0,38 |
0,46 |
3,52 |
|
Параметры ползучести при растяжении |
||||
|
Расчетный интервал |
|
|
|
|
|
Δσp, МПа |
- |
0,5-1,0 |
- |
0,04-0,24 |
|
Еp0, МПа |
- |
5500 |
- |
4000 |
|
Еp∞, МПа |
- |
3537 |
- |
3650 |
|
θПp·105, МПа-1 |
- |
1,56 |
- |
121,5 |
|
λp, сут-1 |
- |
249,6 |
- |
7,5 |
* Аргиллит - порода, обладающая анизотропией механических свойств; в табл. 1 даны непосредственные данные, полученные в экспериментах. Методика обработки опытных данных с учетом анизотропии дана в [25].
Таблица 2
Параметры длительной и остаточной прочностей *
|
Тип породы |
МПа |
МПа |
φ0, φd, φ∞, град |
C0, Cd, C∞, МПа |
φr, град |
Cr, МПа |
|
Туф (район строительства туннеля Арпа-Севан) |
7,26 |
** |
21 |
2,5 |
21 |
0.5 |
|
6,5 |
1,50 |
14 |
2,5 |
|||
|
5,75 |
1,37 |
14 |
2,25 |
|||
|
Известняк (Московский метрополитен) |
** |
** |
** |
** |
41 |
0,2 |
|
10,2 |
** |
43 |
2,24 |
|||
|
8,5 |
** |
40 |
2,0 |
|||
|
Аргиллит *** (Московский метрополитен) |
9,9 |
** |
36 |
2,5 |
31 |
0.15 |
|
3,8 |
** |
35 |
1,0 |
|||
|
2,8 |
** |
21 |
0,75 |
|||
|
Мергель (в оттаявшем состоянии) |
** |
** |
** |
|
27 |
0,23 |
|
4,9 |
0,44 |
34 |
1,63 |
|||
|
2,03 |
0,35 |
29 |
0,6 |
|||
|
Алевролит (Зеленчукская ГЭС) |
** |
** |
* |
* |
36,5 |
0,09 |
|
7,44 |
** |
44 |
1,55 |
|||
|
4,82 |
** |
39 |
1,15 |
|||
|
Гипс (искусственный материал) № 1 |
4,1 |
** |
43 |
0,9 |
39 |
0,2 |
|
3,4 |
0,40 |
35 |
0,9 |
|||
|
2,3 |
0,35 |
26 |
0,9 |
* Параметры сопротивления сдвигу получены в интервале действия нормального напряжения до 2,5 МПа;
** Параметры экспериментально не определялись;
*** Параллельно слоистости.
В табл. 2
параметры пр σмpd, φd,
Cd получены
непосредственно по результатам экспериментов при ступенчатом нагружении
исследуемого массива породы. Параметры ![]()
![]()
![]() определены с использованием параметров φ0,
C0, φd, Cd и φ∞, C∞ по зависимости
определены с использованием параметров φ0,
C0, φd, Cd и φ∞, C∞ по зависимости
![]()
Приложение 5
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ РЕОЛОГИЧЕСКИХ СВОЙСТВ
Представленные ниже примеры определения параметров геологических свойств горных пород привязаны к испытаниям мергеля створа строительства конкретной ГЭС.
Опыты МКН выполнялись на монолитах мергеля, отобраных 13-й экспедицией Ленгидропроекта в штольне № 1001 (правая стенка) с глубины 86 м в мерзлом состоянии при температуре - 4°С на левом берегу.
Фрагмент инженерно-геологического разреза правой стенки, штольни № 1001 на участке отбора монолитов мергеля представлен на рис. 1. По контрольному описанию штольни породы в интервале от 60,0 до 90,0 м от устья представляют образования илгинской свиты - карбонатно-глинистых пород. Цвет пород серый, зеленовато-серый, красновато-коричневый, желтый. Отмечается также пятнистая и невыдержанно-полосчатая окраска. Учитывая, что после завершения строительства гидроузла и заполнения водохранилища произойдет оттаивание горных пород, инженерно-геологическое обследование и испытание монолитов мергеля * было выполнено после его оттаивания при температуре 18°С. Размокаемость исследуемой породы по данным лабораторных опытов незначительная.
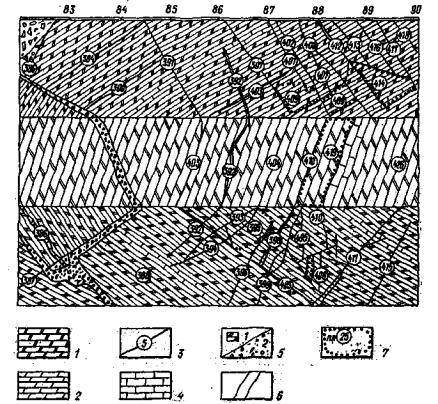
Рис. 1. Фрагмент геологического разреза штольни № 1001 на участке отбора монолитов мергеля
1 - мергель глинистый доломитистый красновато-коричневый с гнездами и линзами зеленовато-серого; 2 - мергель глинистый пестроцветный (зеленовато-серый, коричневый, желтый); 3- трещина, ее номер; 4 - известняк глинистый серый, темно-серый, коричневато-серый, крепкий; 5 - глыбово-щебнистый и щебнисто-дресвяный грунта с суглинком и гравийно-галечный грунт с песком; 6 - крупные трещины отрыва; 7 - контур плоскости трещины, ее номер.
На открытой поверхности монолита мергеля (рис. 2, опыт № 9) выделяются отчетливо видимые системы сомкнутых трещин с шириной раскрытия менее 1 мм. Трещины ожелезнены и содержат включения бурого цвета (лимонит). Общая длина трещин на поверхности под целиком составляет 73 см. Среднее расстояние между ними 2-2,5 см. По степени прерывистости сеть трещин относится к промежуточной. Количество концов трещин на площади равно 3. Величина отношения количества блоков к количеству концов трещин составляет 0,15. Отношение диаметра целика к среднему размеру блока в опытах составляет 4-5, что позволяет рассматривать исследованную породу как квазисплошную и квазиоднородную.
Рис. 2. Зарисовка расположения трещин в основании кольцевого целика
1 - внешний контур кольцевого целика; ~ - трещины; (-) трещины сомкнуты; ширина раскрытия трещин менее 0,01 мм.
Измерение скорости распространения продольных ультразвуковых волн выполнено с помощью прибора УКБ-1М с использованием датчиков, имеющих частоту f = 100 кГц. Средняя скорость распространения упругих волн для монолита № 1 составляет vp = 1,4 км/с. В табл. 1 представлены физико-механические свойства образцов мергеля, определенные по стандартным методикам.
Таблица 1
Физико-механические свойства образцов мергеля
|
Тип породы |
Плотность тв. частиц ρS г/см3 |
Плотность ρ, г/см3 |
Влажность W, % |
Коэффициент пористости |
Временная прочность* |
|
|
на сжатие пр σс, МПа |
на растяжение пр σр, МПа |
|||||
|
Мергель зеленовато-серый |
2,72 |
2,25 |
1,43 |
0,23 |
24,4 |
1,12 |
* Значения пр σ°с и пр σ°р определены по образцам малых размеров неправильной формы на примере пробника БУ-39 по методике ВНИМИ.
* Опыты выполнены В.А. Козионовым и В.П. Колотухиным. Обобщение результатов исследований выполнено В.Л. Кубецким.
Пример 1. Определение условно-мгновенного модуля деформации E0. Исходные данные о перемещениях поверхности массива, полученные в момент его нагружения кольцевой нормальной сжимающей нагрузкой по ступеням, представлены в табл. 2. Нагружение массива осуществлялось кольцевым целиком диаметром 10 см при ξ = 0,6. Испытывался монолит мергеля, опыт № 9.
Таблица 2
Условно-мгновенные осадки поверхности массива
|
Ступень нагружения
Δσс, |
Осадка поверхности основания целика ΔSш0, м·106 |
Осадка поверхности массива вокруг целика ΔSr , м·106 |
|
|
r = 7,5 см |
г- 12,5 см |
||
|
0-0,25 |
7,62 |
3,62 |
1,9 |
|
0,25-0,5 |
15,18 |
5,25 |
2,85 |
|
0,5-0,75 |
13,12 |
4,5 |
2,40 |
|
0,75-1,25 |
25,87 |
11,4 |
3,44 |
|
Расчетный интервал 0,25-1,25 МПа |
ΔS0 |
ΔSr |
|
|
54,17 |
21,15 |
8,69 |
|
|
|
1 1 |
1,40 0,39 |
2,5 0,16 |
Рекомендуется следующий порядок обработки результатов опыта:
1. По исходным данным (табл. 2) строится зависимость осадки основания штампа или целика от нормального напряжения (рис. 3).
2. Определяется расчетный интервал Δσс. В рассматриваемом примере расчетным принят интервал Δσс = 0,25 ÷ 1,25 МПа.
3. По данным о перемещениях поверхности массива в расчетном интервале строится зависимость S0 = f (r) в относительных, координатах (рис. 4). На этот же график наносятся теоретические кривые для различных значений nс = Hса/r (табл. 1 и определяется кривая, наиболее близкая к экспериментальной. В рассматриваемом примере наиболее близкой является кривая при nс = 5,0.
4. По табл. 1 для значения n = 5,0 определяется ωc = 0,468.
5. Определяется модуль условно-мгновенной деформации по формуле
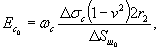
где v - коэффициент относительной поперечной деформации принят равным 0,15.
![]()
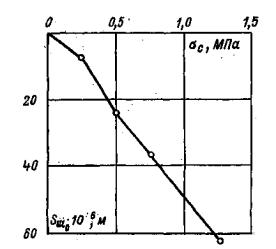
Рис. 3. Зависимость осадки основания кольцевого целика от нормального напряжения
для t = 0.
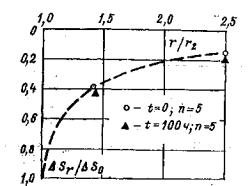
Рис. 4. Осадка поверхности массива вокруг кольцевого целика.
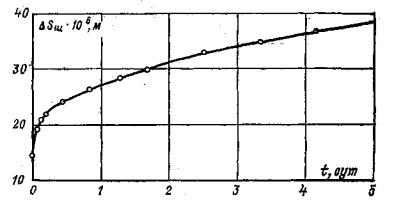
Рис. 5. Осредненная кривая ползучести для Δσс = 0,25 МПа,
Пример 2. Определение параметров ползучести θПσ; λσ; Тσ и модуля деформации Ес∞
Исходными данными являются:
1. Модуль условно-мгновенной деформации Ес0 (см. пример 1).
2. Осредненная кривая ползучести в расчетном интервале σс = 0,25 ÷ 1,25 МПа (рис. 5) для Δσс = 0,25 МПа; Sш0 = 13,6·106 м.
Рекомендуется следующий порядок обработки результатов опыта:
1. Для определения параметров θПσ и λσ используется начальный участок кривой ползучести (3 часа) (рис. 6). Параметры θПσ и λσ определяются графически (рис. 7). Вспомогательные расчеты представлены в табл. 3.
|
|
|
|
Рис. 6. Начальный участок кривой ползучести. |
Рис.
7. Графическое определение |
Таблица 3
Исходные данные для определения параметров ползучести θПσ и λσ
|
Время t·102, сут |
0 |
1,04 |
2,08 |
4,16 |
6,25 |
8,32 |
12,5 |
|
St·106, м |
13,6 |
16,7 |
17,64 |
19,1 |
20,0 |
20,5 |
20,85 |
|
ΔS·106, м |
- |
0,8 |
0,85 |
0,56 |
0,66 |
0,4 |
0,17 |
|
Δt·102, сут |
- |
0,695 |
1,04 |
1,04 |
2,08 |
2,08 |
2,08 |
|
|
- |
1,15 |
0,817 |
0,538 |
0,317 |
0,192 |
0,082 |
|
ΔSк = (St=3 час – S0)·106, м |
- |
7,25 |
7,25 |
7,25 |
7,25 |
7,25 |
7,25 |
|
S (t)/ΔSк |
- |
15,87 |
11,26 |
7,42 |
4,37 |
2,64 |
1,13 |
|
ln (S(t))/ ΔSк |
- |
2,77 |
2,42 |
2,0 |
1,48 |
0,97 |
7,12 |
λσ = tg a = 24,8 сут-1;
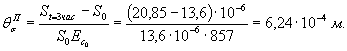
При определенных параметрах λσ и θПσ параметры Тσ и Ес∞ определяем, используя график (рис. 8). Вспомогательные расчеты данны в табл. 4.
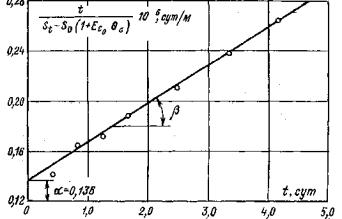
Рис. 8. Графическое определение параметров Тσ и Ес∞.
Таблица 4
Исходные данные для определения параметра ползучести Тσ и модуля деформации Ес∞
|
Время t, сут |
0,416 |
0,832 |
1,25 |
1,67 |
2,5 |
3,33 |
4,16 |
|
St·106, м |
23,73 |
25,87 |
28,15 |
29,7 |
32,6 |
34,8 |
36,6 |
|
S0(1 + Ес0 θПσ) 106, м |
20,8 |
20,8 |
20,8 |
20,8 |
20,8 |
20,8 |
20,8 |
|
St - S0 (1 + Ес0 θПσ) 106, м |
2,93 |
5,07 |
7,35 |
8,9 |
11,8 |
14,0 |
15,8 |
|
St - S0 (1 + Ес0 θПσ) 10-6, сут |
0,142 |
0,164 |
0,172 |
0,188 |
0,212 |
0,238 |
0,2 |
![]()
Tσ = a [Sш∞ - Sш0 (1 + Ec0θПσ)] = 0,136·106·52,6·10-6 – 13,58·10-6 (1 + 857·6,24·10-4) = 4,34 сут.
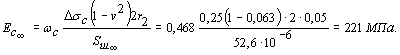
Пример 3. Определение условно-мгновенного модуля деформации при растяжении Epо.
Исходные данные о перемещениях поверхности массива, полученные в момент его нагружения кольцевой растягивающей нагрузкой по ступеням, представлены в табл. 5.
Таблица 5
Условно-мгновенные перемещения поверхности массива
|
Ступени нагружения Δσp, МПа |
Перемещение
поверхности основания целика |
Перемещение поверхности (массива вокруг целика ΔUr м·106 |
|
|
r = 7 см |
r =10,5 см |
||
|
0,04-0,24 |
2,67 |
1,44 |
0,73 |
|
0,24-0,44 |
3,12 |
1,69 |
0,90 |
|
Расчетный интервал Δσp 0,04-0,24 МПа |
ΔUшσ |
ΔUr |
|
|
2,67 |
1,44 |
0,72 |
|
|
r/r2 ΔUr/ΔU0 |
1 1 |
1,4 0,54 |
2,1 0,27 |
|
|
|
|
Рис. 9. Зависимость подъема основания целика от растягивающего напряжения. |
Рис. 10. Перемещения поверхности массива за пределами загруженной поверхности. |
Рекомендуется следующий порядок обработки результатов опыта:
1. По исходным данным строится зависимость подъема поверхности основания от нормального растягивающего напряжения (рис. 9).
2. Принимается расчетный интервал Δσp. Так как зависимость U = f (σp), как правило, имеет существенно нелинейный характер, то модуль деформации Ер0 рекомендуется определять для каждой ступени. В рассматриваемом примере принят интервал Δσp = 0,04 ÷ 0,24 МПа.
3. По данным о перемещениях поверхности массива в расчетном интервале строится зависимость ΔUr = f (r) в относительных координатах (рис. 10). На этот же график наносятся теоретические кривые, наиболее близкие для различных значений nc = Нса/r2, и определяется кривая, наиболее близкая к экспериментальной. В рассматриваемом примере наиболее близкой является кривая nс = ∞.
4. По табл. 1 (раздел 6) для nс = ∞ определяются ωс = 0,541.
5. Определяется модуль условно-мгновенной деформации по формуле
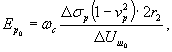
где vp - коэффициент' относительной поперечной деформации при растяжении, принят равным 0,25.
![]()
Пример 4. Определение параметров ползучести θПp и λp при растяжении и модуля деформации Ep∞.
Исходными данными являются:
1. Модуль условно-мгновенной деформации Epо (см. пример 3).
2. Кривая ползучести в расчетном интервале Δσp = 0,04 ÷ 0,24 Мпа, ΔUшc = 2,67·10-6, м (рис. 11).
|
|
|
|
Рис. 11. Кривая ползучести на ступени |
Рис. 12. График для определения параметров ползучести θПp и λp. |
Рекомендуется следующий порядок обработки результатов опыта:
1. В связи с тем, что на ступени была достигнута практически полная стабилизация деформаций, для определения параметров θПp и λp используется вся кривая ползучести. Параметры θПp и λp определяются графически (рис. 13). Вспомогательные расчеты представлены в табл. 6.
λp = tg a·= 7,6 сут-1
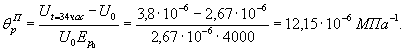
Таблица 6
Исходные данные для определения параметров ползучести θПp и λp
|
Время t·102, сут |
0 |
4,16 |
8,32 |
16,64 |
41,6 |
58,24 |
83,2 |
|
Uш·106, м |
2,67 |
3,0 |
3,2 |
3,5 |
3,8 |
3,8 |
3,8 |
|
ΔUш·106, м |
- |
0,27 |
0,18 |
0,1 |
0,047 |
- |
- |
|
Δt·102, сут |
- |
2,08 |
2,08 |
2,08 |
2,08 |
- |
- |
|
|
- |
13,0 |
8,65 |
4,8 |
2,26 |
- |
- |
|
ΔUк = (Ut=34 час – U0)·106, м |
- |
0,13 |
0,13 |
0,13 |
0,13 |
0,13 |
0,13 |
|
U (t)/ΔUк·10сут/м |
- |
10 |
6,65 |
3,7 |
1,73 |
- |
- |
|
ln U(t))/ ΔUк |
- |
4,6 |
4,19 |
3,61 |
1,75 |
- |
- |
2. При определенных параметрах λp и θПp определяется параметр Ep∞ по формуле
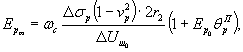
![]()
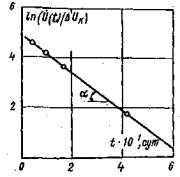
Рис. 13. Кривая ползучести на ступени Δσp = 0,04 ÷ 0,44 Мпа.
3. Строится кривая ползучести на ступени Δσp = 0,04 ÷ 0,44 Мпа (рис. 12). На данной ступени произошел отрыв целика (разрушение основания) через 1 ч с момента нагружения ступени.
4. Определяется предел длительной прочности при растяжении пр σp∞. В связи с тем, что при действии растягивающего напряжения σp = 0,24 МПа деформации ползучести имели явно выраженный затухающий характер, а при σp = 0,44 МПа произошел отрыв кольцевого целика от основания, предел длительной прочности мергеля при растяжении составляет 0,24 МПа.
Пример 5. Определение условно-мгновенного модуля G0.
Исходные данные о перемещениях поверхности массива, полученные в момент его нагружения кольцевой касательной нагрузкой по ступеням, представлены в табл. 7. Нагружение массива осуществлялось кольцевым целиком диаметром 10 см при ξ = 0,6. Испытывался монолит мергеля (опыт № 9), при σс = 0,76 МПа.
Рекомендуется следующий порядок обработки результатов опыта:
1. По, исходным данным (табл. 7) строится зависимость горизонтальных перемещений поверхности основания штампа или целика от нормального напряжения (рис. 14).
Таблица 7
Условно-мгновенные перемещения поверхности массива
|
Ступень нагружения |
Горизонтальные
перемещения-поверхности основания целика Δδ0, |
Горизонтальные перемещения поверхности массива вокруг целика Δδr , м·106 |
|
|
r = 7,5 см |
r = 12,5 см |
||
|
0-0,25 |
3,7 |
0,4 |
0 |
|
0,25-0,5 |
5,6 |
0,5 |
0 |
|
0,5-0,75 |
5,88 |
0 |
0 |
|
0,75-1,0 |
7,75 |
0 |
0 |
|
1,0-1,25 |
9,37 |
0 |
0 |
|
1,25-1,5 |
10,25 |
0 |
0 |
|
|
|
|
Рис. 14. Зависимость условно-мгновенных горизонтальных перемещений основания кольцевого целика от касательного напряжения. |
Рис. 15. Горизонтальные перемещения поверхности основания за пределами загруженной поверхности. |
2. В связи с тем, что зависимость δ0 = f (σp) имеет нелинейный характер, то модули сдвига G0 рекомендуется определять для каждой ступени нагружения.
3. По данным о перемещениях поверхности массива для каждой ступени строятся зависимости Δδ0 = f (r) в относительных координатах (рис. 15). На этот график наносятся теоретические кривые для различных значений nк = Haк/r2 и определяется кривая, наиболее близкая к экспериментальной.
4. Для первой ступени нагружения Δτ1 = 0 ÷ 0,25 МПа (рис. 15) наиболее близкой является кривая при n = 0,4.
5. По табл. 2 (раздела 6) для значения n = 0,4 определяется ωк1 = 0,131.
6. Определяется условно-мгновенный модуль сдвига по формуле
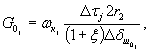
![]()
7. Аналогичным образом определяется величина условно-мгновенного сдвига для следующих ступеней нагружения (табл. 8).
Таблица 8
Результаты расчета Goj и γ0
|
j |
Ступени нагружения |
Haк/r2 |
ωkj |
G0j , МПа |
Δγ0j·104 |
γ0·104 |
|
1 |
0-0,25 |
0,4 |
0.131 |
553 |
4,52 |
4,52 |
|
2 |
0,25-0,5 |
0,4 |
0,131 |
366 |
6,83 |
11,35 |
|
3 |
0,5-0,75 |
0,2 |
0,083 |
220 |
11,4 |
22,75 |
|
4 |
0,75-1,0 |
0,2 |
0,083 |
167 |
15,0 |
37,75 |
|
5 |
1,0-1,25 |
0,2 |
0,083 |
138 |
18,13 |
55,88 |
|
6 |
1,25-1,5 |
0,2 |
0,083 |
126 |
19,87 |
75,75 |
8. Определяется величина приращения условно-мгновенной относительной деформации сдвига на ступени нагружения по формуле
Δγoj = Δτj/G0j,
Δγ01 = 0,25/553 = 4,52·10-4.
|
|
|
|
Рис. 16. Зависимость условно-мгновенного модуля сдвига от касательного напряжения. |
Рис. 17. Зависимость γi0 = f (τi) |
9. Определяется величина полной относительной деформации сдвига γ0 путем суммирования деформаций сдвига, полученных на ступенях, нагружения (табл. 8):
γ0 = γ01 + γ02 + γ03 + ¼ + γ0j
10. Данные расчета представлены в табличной (табл. 8) и графической (рис. 16, 17) формах.
Пример 6. Определение параметров ползучести θПτj; λτj; Tτj; G∞j.
Исходными данными являются:
1. Условно-мгновенный модуль сдвига G0j (см. пример 5).
2. Кривые ползучести по ступеням ∆τj (рис. 18).
Рекомендуется следующий порядок обработки результатов опыта.
1. Для определения параметров θПτ1 и λτ1 на первой ступени ∆τ1 = 0 ÷ 0,25 МПа используется начальный участок кривой ползучести (рис. 19). Параметры θПτ1 и λτ1 определяются графически (рис. 20). Вспомогательные расчеты представлены в табл. 9.
Рис. 18. Кривые ползучести мергеля на ступенях действия касательного напряжения:
a-Δτ1 = 0 ÷ 0,25 МПа; б-Δτ2 = 0,25 ÷ 0,5 МПа; в-Δτ3 = 0,5 ÷ 0,75 МПа; г-Δτ4 = 0,75 ÷ 1 МПа;
д-Δτ5 = 1 ÷ 1,25 МПа; е-Δτ6 = 1,25 ÷ 1,15 МПа;
1 – зависимость δшt = f (τ); 2 – зависимость SDш = f (t).
Таблица 9
Исходные данные для определения параметров ползучести
|
Время t·102, сут |
0 |
1,04 |
2,08 |
4,16 |
6,25 |
8,12 |
12,5 |
|
δt·106, м |
3,07 |
3,76 |
4,14 |
4,58 |
4,82 |
5,15 |
5,2 |
|
Δδt·106, м |
- |
0,38 |
0,36 |
0,45 |
0,28 |
0,24 |
0,04 |
|
Δt·102, сут |
- |
1,04 |
1,04 |
2,08 |
2,08 |
2,08 |
2,08 |
|
δt = Δδ/Δt·104 м/сут |
- |
0,366 |
0,346 |
0,214 |
0,135 |
0,115 |
0,04 |
|
Δδк = (δt=3час - δо)·106, м |
- |
2,14 |
2,14 |
2,14 |
2,14 |
2,14 |
2,14 |
|
δt/ Δδк, 1/сут |
- |
17,2 |
16,1 |
10,0 |
6,3 |
5,37 |
1,87 |
|
ln (δt/ Δδк) |
1'"-' |
2,84' |
2,78 |
2,3 |
1,84 |
1,68 |
0,6 |
|
|
|
|
Рис. 19. Начальный участок кривой ползучести на ступени Δτi = 0 ÷ 0,25 МПа. |
Рис. 20. График для определен параметров ползучести θПτ и λτ |
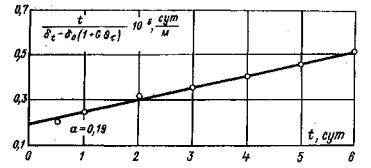
Рис. 21. График для определения параметра Tσ, и величины G∞
λτ = tg a = 19,0 сут-1,
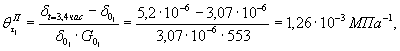
2. При определенных параметрах θПτ1 и λτ1 параметры Tτ1 и G∞1 определяются по графику (рис. 21). Вспомогательные расчеты представлены в табл. 10.
Таблица 10
Исходные данные для
определения параметра ползучести Tτ
и
модуля сдвига G∞1
|
Время t, сут |
0,5 |
1 |
1,5 |
2 |
3 |
4 |
5 |
6 |
|
δt·106, м |
7,7 |
9,2 |
10,9 |
11,8 |
13,6 |
15,05 |
16,1 |
16,8 |
|
δ01 (1 + G01θПτ1) 106, м |
5,2 |
5,2 |
5,2 |
5,2 |
5,2 |
5,2 |
5,2 |
5,2 |
|
δt·- δ01 (1 + G01θПτ1) 106, м |
2,5 |
4,0 |
5,7 |
6,6 |
8,4 |
9,75 |
10,9 |
11,6 |
|
|
0,20 |
0,25 |
0,263 |
0,315 |
0,357 |
0,41 |
0,46 |
0,517 |
![]()
Tτ = a [δ∞1 – δ01 (1 + G01θПσ1)] = 0,19·10-6·[23,7·10-6 – 5,2·10-6] = 3,52 сут.
![]()
3. Определяется величина приращения стабилизированной относительной деформации сдвига на ступени нагружения:
Δγ∞1 = Δτ1/G∞1 = 0,25/36,5 = 2,9·10-3.
4. Аналогичным образом по кривым ползучести, полученным на следующих ступенях нагружения (рис. 18), определяются параметры ползучести величины стабилизированного модуля сдвига, а также величина полной стабилизированной относительной деформации сдвига γ∞ путем суммирования деформации сдвига, полученных на ступенях нагружения:
Данные расчетов представляются в табл. 11.
Таблица 11
Результаты расчета параметров ползучести θПτj; λτj; Тτj и параметра G∞1
|
j |
Ступень нагружения |
θПτ·103 |
λτ, 1/сут |
Тτ сут |
G∞, МПа |
Δγ∞ |
γ∞·103 |
|
1 |
0-0,25 |
1,26 |
19,0 |
3,52 |
86,5 |
2,9 |
2,9 |
|
2 |
0,25-0,5 |
1,95 |
16,6 |
2,74 |
56,2 |
4,45 |
7,35 |
|
3 |
0,5-0,75 |
13,1 |
44,0 |
3,42 |
13,9 |
1,8 |
25,35 |
Примечание. В табл. 11 даны параметры ползучести для первых трех ступеней, где был получен затухающий во времени характер деформации ползучести (рис. 22).
На ступени Δτ4 = 0,75 ÷ 1,0 МПа был получен незатухающий во времени характер деформаций ползучести, что следует из анализа результатов представления кривой ползучести на данной ступени в полулогарифмических координатах (рис. 23). Кроме того, начиная с данной ступени, был зафиксирован значительный подъем основания кольцевого целика (рис. 18, г). Отсюда следует, что величина τ = 1.0 МПа превышает предел длительной прочности. Предел длительной прочности в данном опыте составляет пр τ∞ = 0,75 МПа.
|
|
|
|
Рис. 22 Зависимость (δшt - δш0) f (t) на ступени Δτ = 0,75 ÷ 1 МПа в полулогарифмических координатах. |
Рис. 23. Зависимость (δшt - δш0) = f (t) на ступени Δτ = 0,5 ÷ 0,75 МПа в полулогарифмических координатах. |
5. Получение вида зависимостей γi = f (τi; t) для различных моментов времени и определения параметров А (t) и m. выполняются в следующей последовательности:
а) Определяется величина модуля сдвига для различных моментов времени по ступеням нагружения по формуле
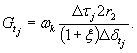
б) Определяется величина относительной деформации сдвига для рассматриваемого момента времени:
Данные расчетов, представлены в табл. 12.
Таблица 12
Результаты расчета Gtj и γtj
|
Ступень нагружения Δτ, МПа |
Время t, сут |
|||||
|
0 |
1 |
3 |
6 |
∞ |
||
|
0-0,25 |
Gt1, МПа |
553 |
209 |
150,5 |
122 |
86,5 |
|
γt1·104 |
4,52 |
11,95 |
16,6 |
20,5 |
2,9 |
|
|
0,25-0,5 |
Gt2, МПа |
366 |
133,5 |
86,5 |
72,6 |
56,2 |
|
γt 2·104 |
6,83 |
18,7 |
28,9 |
39,8 |
44,5 |
|
|
0,5-0,75 |
Gt3, МПа |
220 |
29,5 |
23 |
18,6 |
13,9 |
|
γt3·104 |
11,4 |
85 |
109 |
134 |
180 |
|
в) Определяется величина относительной деформации сдвига γi для различных моментов времени t путем суммирования деформаций, а полученных на различных ступенях (табл. 12). Результаты расчетов представлены в табл. 13 и на рис. 24.
Таблица 13
Результаты расчета γit = f (τi)·104
|
τi |
Время t, сут |
||||
|
0 |
1 |
3 |
6 |
∞ |
|
|
0,25 |
4,52 |
11,95 |
16,6 |
20,5 |
29 |
|
0,5 |
11,35 |
30,65 |
45,5 |
60,3 |
73,5 |
|
0,75 |
22,75 |
103,7 |
137,8 |
173,8 |
253,5 |
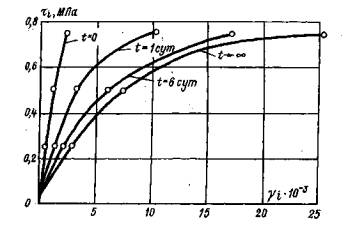
Рис. 24. Зависимости γi = f (τi) для различных моментов времени.
г) Для определения параметров At и m зависимости γit = f (τi; t) для различных моментов времени (рис. 24) представляются в логарифмических координатах (рис. 25). Результаты расчёта представлены в табл. 14.
Таблица 14
Значения ln τi и ln γi для различных моментов времени
|
ln τi |
Время t, сут |
||||
|
0 |
1 |
3 |
6 |
∞ |
|
|
-1,38 |
-7,7 |
-6,73 |
-6,41 |
-6,19 |
-5,85 |
|
-0,9 |
-6,78 |
-5,79 |
-5,59 |
-5,1 |
-4,91 |
|
-0,29 |
-6,09 |
-4,56 |
-4,29 |
-4,05 |
-3,67 |
Анализ опытных данных, представленных на рис. 25, показывает, что для данного типа грунта параметр т с достаточной точностью может быть принят постоянным для различных моментов времени, а его величина равна m = 0,61. В табл. 15 и на рис. 26 даны величины параметра A(t) для различных моментов времени.
|
|
|
|
Рис. 25. Зависимости γit = f (τi; t) в логарифмических координатах |
Рис. 26. Зависимость изменения параметра At во времени. |
Таблица 15
Значения параметра At для различных моментов времени
|
Время t, сут |
0 |
1 |
3 |
6 |
∞ |
|
At, МПа |
6,76 |
3,53 |
2,48 |
2,06 |
1,84 |
6. Величина приращения относительной деформации объема ΔεDvj; на ступени касательного напряжения для различных моментов времени определяется по зависимости
![]()
Для первой ступени нагружения Δτ1 = 0 ÷ 0,25 МПа. На Hка = 0,02 м для момента времени t = 0 ΔS = 1,2·10-6 м, тогда для t = 0:
![]()
Аналогичным образом выполняется расчет ΔεDv для различных моментов времени и для других ступеней нагружения. Исходные данные и результаты расчетов даны в табл. 16.
Таблица 16
Результаты расчета ΔεDvj для различных моментов времени
|
j |
Ступень нагружения Δτ, МПа |
Время t, сут |
||||
|
0 |
1 |
3 |
6 |
|||
|
1 |
0-0,25 |
ΔSDш·106 м |
1,2 |
3,3 |
8 |
16 |
|
ΔεDv·104 |
1,2 |
3,3 |
8 |
16 |
||
|
2 |
0,25-0,50 |
ΔSDш·106 м |
1,5 |
1,8 |
8 |
10 |
|
ΔεDv·104 |
1,5 |
1,8 |
8 |
10 |
||
|
3 |
0,50-0,75 |
ΔSDш·106 м |
-1 |
-1 |
-3 |
2 |
|
ΔεDv·104 |
-0,5 |
-0,5 |
-1,5 |
1 |
||
|
4 |
0,75-1,0 |
ΔSDш·106 м |
-3,3 |
-2,1 |
-24 |
-28 |
|
ΔεDv·104 |
-1,6 |
-10,5 |
-12 |
-14 |
||
|
5 |
1.0-1,25 |
ΔSDш·106 м |
-9 |
-30 |
-42 |
-48 |
|
ΔεDv·104 |
-4,5 |
-15 |
-21 |
-24 |
||
|
6 |
1,25-1,5 |
ΔSDш·106 м |
-22 |
-89 |
-100 |
∞ |
|
ΔεDv·104 |
-11 |
-44,5 |
-50 |
∞ |
||
По данным табл. 16 определяется полная величина приращения относительной деформации объема, соответствующая полной величине касательного напряжения на ступени путем суммирования величин ΔεDvj, полученных на ступенях нагружения. Результаты расчетов представлены в табличной (табл. 17) и графической (рис. 27) формах.
Таблица 17
Значения εDv·104 для различных моментов времени
|
τi, МПа |
Время t, сут |
|||
|
0 |
1 |
3 |
6 |
|
|
εDv·104 |
||||
|
0,25 |
1,2 |
3,3 |
8 |
16 |
|
0,5 |
2,7 |
51 |
16 |
26 |
|
0,75 |
2,2 |
4,6 |
14,5 |
27 |
|
1,0 |
0,6 |
-4,9 |
2,5 |
13 |
|
1,25 |
-3,9 |
-19,9 |
-18,5 |
-11 |
|
1,5 |
-14,9 |
-64,4 |
-68,5 |
-∞ |
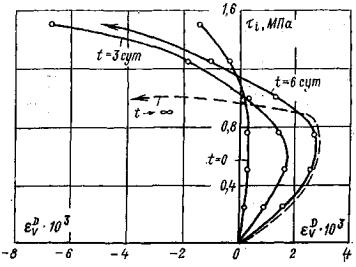
Рис. 27. Зависимости εDv = f (τi) для различных, моментов времени.
7. Выполняется расчет, величины коэффициента относительной поперечной деформации для стабилизированного состояния:
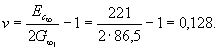
Приложение 6
ОБРАБОТКА ФАКТИЧЕСКОГО МАТЕРИАЛА О КРИОГЕННОМ СТРОЕНИИ СКАЛЬНЫХ И
ПОЛУСКАЛЬНЫХ ГРУНТОВ
1. При промерзании скальных пород лед в основном наследует уже существующие пустоты (трещины). В определенных условиях в процессе криогенеза происходит перераспределение пустотности, морозное разуплотнение (распучивание) пород. Анизотропия трещиноватости, свойственная скальным породам в массиве, при промерзании преобразуется, в ряде случаев различно направленные трещины по разному заполняются льдом, распученность массива может быть значительна лишь в определенном направлении. Кроме того, различные системы трещин в разной степени влияют на работу сооружений.
2. Основными задачами изучения криогенного строения скальных пород являются установление закономерностей изменения характера, степени их трещиноватости, льдонасыщенности и выявление зон (участков), распученных при промерзании.
Для оценки анизотропии криогенного строения и прогноза изменения свойств мерзлого скального массива при оттаивании необходимо оценивать криогенное строение с учетом каждой из выделенных при геолого-структурных исследованиях систем трещин.
Рис. 1. Характер распространения, ширина и тип заполнения трещин
Системы трещин: 1 - пологая; 2 - крутопадающая, ориентированная вдоль долины; 3 - крутопадающая, ориентированная поперек долины; 4 - наклонная; степень и тип заполнения трещин; 5 - полая; 6 - кристаллический заполнитель; 7 - корочки и пленки льда; 8 - мерзлый мелкозем; 9 - лед; 10 - контакты за счет соприкосновения стенок трещины или кристаллического заполнителя; трещины и зоны, учитывающиеся индивидуально; 11 - трещина с раскрытием более 100 мм (в знаменателе - величина раскрытия); 12 - тектоническая зона; 13 - зона сильнотрещиноватых пород (модуль трещиноватости более 10); 14 - зона интенсивного выветривания; 15 - ориентировочное значение Кт.п.; 16 - значение Кт.п./Л по опытным данным.
3. Льдистость во взаимосвязи с трещиноватостью и распученность в пределах тектонических зон, имеющих индивидуальное инженерно-геологическое значение, оцениваются отдельно.
4. Указанные положения учтены в методике документации горных выработок в мерзлых скальных и полускальных грунтах, изложенной в «Руководстве по документации горных выработок в мерзлых скальных породах Р-1/73 Ленгидропроект. Настоящее приложение по обработке фактического материала о криогенном строении скальных пород является его продолжением при изучении криогенного строения скальных и полускальных грунтов для их инженерно-геологической оценки как среды, вмещающей подземное гидросооружение.
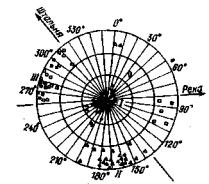
Рис. 2. Диаграмма распределения трещин по падению.
5. Обработку полученного при целенаправленной документации фактического материала по криогенному строению скальных пород следует вести по определенной форме, представляющей собой сводный лист, который состоит из таблиц, графиков и диаграмм. На рис. 1-4 настоящего приложения приводится пример заполнения сводного листа для мерзлых скальных и полускальных грунтов интрузивного типа.
6. Приступая к обработке материала для составления сводного листа, необходимо ознакомиться с геологическим строением массива, в котором пройдена горная выработка, и выделить однородные в геолого-структурном отношении и аномальные участки. В пределах этих участков обработка фактического материала ведется по системам трещин.
7. По данным документации выработки составляется диаграмма распределения трещин по падению. Принадлежность трещин к определенной системе отображается условным знаком, кроме того, цветом показывается степень заполнения и тип заполнителя трещин. На диаграмму также: наносят направление долины, направление выработки, в необходимых случаях направление осей сооружений.
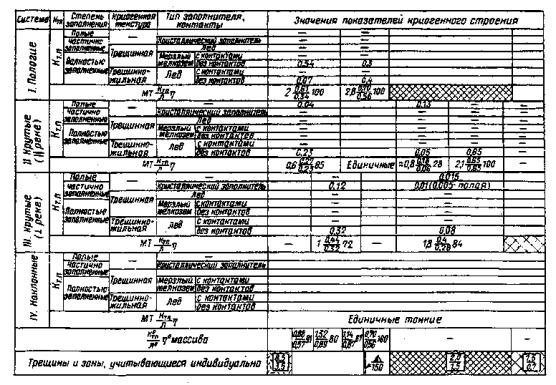
Рис. 3. Количественная характеристика криогенного строения.
8. После разделения трещин на системы составляются зарисовки следов трещин для каждой системы. Плоскости для зарисовок должны быть ориентированы в направлении, близком перпендикулярному в данной системе. Для наглядности и удобства обработки рекомендуется на одну зарисовку наносить не более двух систем трещин. Для отображения пологих трещин (I система) используется правая стенка штольни, для отображения крутопадающих трещин (II - III системы) выбрана кровля штольни. Зарисовки отражают характер распространения и частоту трещин, характер и тип заполнения, наличие и характер контактов. Принадлежность трещин к определенной системе отображается типом линий (сплошная, пунктирная и т.д.), цветом - тип заполнения и особым знаком - контакты. На зарисовках сохраняется номер трещины, присвоенный ей при документации выработки.
Рис. 4. Графики изменения
Кт.п (по системам), Кт.п, Л° по выработке.
На этих зарисовках выделяются трещины и зоны, которые необходимо анализировать особо, поскольку в расчетах сооружений они учитываются индивидуально. К ним рекомендуется относить: а) трещины, ширина которых превышает 100 мм; б) тектонические зоны; в) зоны сильно трещиноватых грунтов (модуль трещиноватости больше 10 т/м); г) зоны интенсивного выветривания и т.д.
Количественная характеристика криогенного строения для перечисленных структурных элементов массива ведется особо.
По типу заполнения выделяются трещины: а) полые; б) частично заполненные кристаллическим заполнителем, льдом; в) полностью заполненные льдом, мерзлым мелкоземом.
Тип заполнителя показывается цветовой раскраской следов трещин. Кроме того, особым знаком отображаются контакты за счет соприкосновения стенок трещин, либо выполнения участков трещин на все сечения кристаллическим заполнителем.
9. Под зарисовками строится график, иллюстрирующий основные характеристики трещин. На графике условным знаком по оси абсцисс показывается положение каждой трещины по глубине (длине) выработки, а по оси ординат в полулогарифмическом масштабе - средняя ширина трещин в мм. Цветом отражается заполнитель трещин и особым знаком - наличие контактов. График дает наглядное представление о взаимосвязи ширины трещин и типа заполнителя и характере изменения этих показателей по выработке.
10. Полученный таким образом материал позволяет выделить участки с различными криогенными текстурами и провести количественную оценку основных характеристик криогенного строения скальных и, полускальных грунтов по системам трещин.
Расчету характеристик криогенного строения предшествует разделение выработки на участки с различной частотой трещин, с различным типом или степенью их заполнения и на участки, резко различающиеся по ширине трещин. Участки, выделенные для расчета, должны содержать не менее 5 трещин данной системы. Для участков, где это условие не соблюдается, подсчет характеристик для системы не производится. В результате за счет всех систем трещин на таком участке значения характеристик криогенного строения ориентировочны и сопровождаются особым знаком (≈).
Криогенное строение характеризуют следующие показатели:
а) Модуль трещиноватости (МТ) - частота трещин в массиве, характеризующаяся количеством трещин, приходящихся на 1 п. м породы по перпендикуляру к системе.
б) Коэффициент трещинной пустотности, %: по системам линейный (Кт.п.), представляющий собой отношение суммарной ширины трещин на измеряемом участке к его длине, для массива - объемный (К°т.п.), получаемый суммированием линейных по системам.
в) Льдистость, %: по системам - линейная (Л), представляющая собой отношение суммарной мощности льда в трещинах на измеряемом участке к его длине, для массива - объемная (Л°), получаемая суммированием линейных по системам. Льдистость подсчитывается следующим образом: к Кт.п. за счет трещин, выполненных льдом (при частичном выполнении льдом Кт.п. принимается с коэффициентом, учитывающим степень выполнения, например, для трещин, выполненных льдом на 80%, коэффициент равен 0,8), прибавляется Кт.п. за счет трещин, выполненных мерзлым мелкоземом, принимаемый с коэффициентом, зависящим от влажности (льдистости) заполнителя (например, при W = 30 % этот коэффициент равен 0,3; для трещин, выполненных мерзлым мелкоземом со шлирами льда, влажность обычно 50 % и более, следовательно, и упомянутый коэффициент будет 0,5 и выше).
г) η - показатель распученности, представляющий собой долю коэффициента трещинной пустотности (линейного, объемного), обусловленную трещинами, которые подверглись или могли подвергнуться процессам распучивания. В настоящее время такими трещинами следует считать трещины, выполненные на все сечение льдом либо мерзлым мелкоземом, т.е. трещины без контактов любого типа.
В итоге, каждый выделенный участок по каждой системе трещин характеризуется формулой
![]()
Для данного участка массива за счет всех систем трещин характеристика криогенного строения приводится в виде формулы
![]()
11. Для установления закономерностей изменения основных показателей криогенного строения по выработке строятся графики изменения льдистости и коэффициента трещинной пустотности по системам трещин и суммарных, позволяющие судить о взаимосвязи льдистости с пустотностью.
12. Все трещины и зоны, учитываемые индивидуально, наносятся на графики сводного листа особыми знаками. Для количественной оценки криогенного строения в их пределах необходимы специальные исследования (лабораторные, натурные). Места проведения таких работ отражаются на зарисовке условными знаками. Обработка материалов этих исследований и их результаты представляются дополнительно.
Приложение
7
ЖУРНАЛ ИСПЫТАНИЙ МЕРЗЛЫХ (ОТТАЯВШИХ) ГОРНЫХ ПОРОД МЕТОДОМ
КОЛЬЦЕВОГО НАГРУЖЕНИЯ
Испытание № ______
|
Наименование организации _______________________________________ _______________________________________ Внутренний и наружный радиусы кольцевого целика (штампа) r1, см; r2 см ________________________________________ Площадь целика (штампа) ____________см2 Тип теплоэлектронагревательного оборудования ________________________________________ Абсолютная отметка подошвы целика (штампа) ________________________________________
|
Объект ______________________________________ ______________________________________ Сооружение ______________________________________ Пункт ______________________________________ Дата испытания: Начало _______________________________ Окончание ____________________________ |
|
Глубина залегания испытываемого массива, _______ м Наименование
испытываемой породы ________________________________________________________________________________ ________________________________________________________________________________ Краткая характеристика установки для испытаний ____________________________________ ________________________________________________________________________________ Ответственный исполнитель _______________________________________________________ Наблюдатели ____________________________________________________________________ Адрес организации_______________________________________________________________ |
|
Приложение 8
ТЕХНИЧЕСКАЯ ХАРАКТЕРИСТИКА НАГРУЗОЧНОГО И ИЗМЕРИТЕЛЬНОГО ОБОРУДОВАНИЯ
|
Домкраты № ____________________________________________________________________ Грузоподъемность домкратов: вертикальных ________________________________________________________________ горизонтальных ______________________________________________________________ Манометры: № и их краткая характеристика _________________________________________ _______________________________________________________________________________ Температурные датчики и их краткая характеристика _________________________________ _______________________________________________________________________________ Схематический
план расположения установки
|
Приложение 9
Страницы журнала
Объект __________________Выработка № _______________Испытание №________________
Данные наблюдений за перемещениями основания в процессе его нагружения
|
Дата |
Этап испы- |
Время проведе- |
Пока- |
Нагрузка на целик (штамп) КН (ТС) |
Давление по подошве целика (штампа) Мпа, (кгс/см2) |
Показания датчиков вертикальных деформаций, мм |
Показания датчиков горизонтальных деформаций, мм |
Показания температурных датчиков |
Примечание |
||||||||||||
|
№ 1в |
№ 2в |
№ 3в |
№ 4в |
|
№ 1г |
№ 2г |
№ 3г |
№ 4г |
|
№ 1 |
№ 2 |
№ 3 |
№ 4 |
|
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
|
15 |
16 |
17 |
18 |
|
19 |
Ступени нагружения
Приложение 10
Объект __________________Выработка № _______________Испытание №________________
Таблица обработки экспериментальных данных на ступени нагружения (разгрузки)
|
Время отсчета час, мин |
Время между отсчетами |
Время с момента
нагруж. |
Величина деформации между отсчетами по реперам на целике (штампе), мм |
Средняя деформация между отсчетами, мм |
Общая деформация от начала нагружения ступени |
Величина деформация между отсчетами для группы равноотстоящих от целика , мм реперов |
Средняя деформация между отсчетами, мм |
Общая деформация от начала нагружения ступени, мм |
||||||
|
№ 1 |
№ 2 |
№ 3 |
№ 4 |
№ 1 |
№ 2 |
№ 3 |
№ 4 |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
СПИСОК ЛИТЕРАТУРЫ
1. А. с. № 657315 СССР, МКИ 4 G 01 N 3/08; 3/22. Способ испытания грунтов/В.Л. Кубецкий//Открытия. Изобретения. 1979. № 14.
2. А. с. № 654877 СССР, МКИ4 G 01 N 3/22; Е 02 Д 1/02. Способ определения сопротивления грунта сдвигу/В.Л. Кубецкий//Открытия. Изобретения. 1979. № 12.
3. А. с. № 663776 СССР, МКИ4 Е 02 Д 1/02. Способ определения деформируемости массивных сред и прочности их контакта с бетоном / В.Л. Кубецкий // Открытия. Изобретения. 1979. № 5.
5. Булычев Н.С. Механика подземных сооружений. М.: Недра, 1982.
6. Возведение обделок подземных гидротехнических сооружений в вечномерзлых скальных грунтах. ВСН 36-86. Минэнерго СССР. Л.: ВНИИГ, 1986.
7. Вялов С.С. Реологические основы механики грунтов. М.: Высшая школа, 1978.
8. Гольдин А.Л., Рассказов Л.Н. Проектирование грунтовых плотин. М.: Энергоиздат, 1987.
9. Гудман Р. Механика скальных пород; М.: Стройиздат, 1987.
10. Джегер Ч. Механика горных пород, и инженерные сооружения. М.: Мир, 1975.
12. Ержанов Ж.С. Теория ползучести горных пород и ее приложения. Алма-Ата: Наука, 1964.
13. Зарецкий Ю.К. Теория консолидации грунтов. М.: Наука, 1967.
14. Зарецкий Ю.К., Ломбарде В.Н. Статика и динамика грунтовых плотин. М.: Энергоатомиздат, 1983.
15. Зенкевич О. Метод конечных элементов в технике. М.: Мир, 1975.
16. Иванов П. Л. Грунты и основания гидротехнических сооружений. М.: Высшая школа, 1985.
20. Кубецкий В.Л. Закономерности ползучести и длительной прочности трещиноватых скальных пород по результатам ролевых исследований // Труды первого Всесоюзного симпозиума по реологии грунтов. Ереван: Ереванский ун-т, 1973. С. 234-246.
22. Кубецкий В.Л., Козионов В.А. Напряженно-деформированное состояние слоя, подстилаемого несжимаемым основанием при действии кольцевой нагрузки. Деп. во ВНИИС, № 2335. М.: 1981.
24. Кубецкий В.Л., Шрамкова В.Н., Колотухин В.П. Оценка точности определения параметров сопротивления сдвигу горных пород. Деп. во ВНИИС, № 4184. М., 1983.
25. Кубецкий В.Л., Семенов В. В., Королев М.В. Определение характеристик деформируемости трансверсально-изотропных трещиноватых пород по результатам штамповых испытаний // Приложение численных методов к задачам геомеханики. М.: МИСИ, 1986. С. 22-23.
29. Малышев М.В. Прочность грунтов и устойчивость оснований сооружений. М.: Стройиздат, 1980.
32. Прочухан Д.П., Фрид С.А., Доманский Л.К. Скальные основания гидротехнических сооружений. Л.: Стройиздат, 1971.
34. Рекомендации по изучению напряженного состояния пород сейсмоакустическими методами/ Под ред. А.И. Савича, Б.Д. Куюнджича. Москва-Белград. Гидропроект им. С.Я. Жука, 1986.
40. Рекомендации по применению инженерной геофизики для изучения деформационных свойств скальных горных массивов / Под. ред. А.И. Савича, Б.Д. Куюнджича. Москва-Белград. Гидропроект им. С.Я. Жука, 1985.
44. Руководство по проектированию гидротехнических туннелей. М.: Стройиздат, 1982.
45. СНиП 2.02.02-85. Нормы проектирования. Основания гидротехнических сооружений. М.: Стройиздат, 1985.
46. СНиП 2.06.09-84. Нормы проектирования. Туннели гидротехнические. М.: Стройиздат, 1985.
47. Ставрогин А.Н., Протосенян А.Г. Пластичность горных пород. М.: Недра, 1979.
48. Введение в механику скальных пород /Д.X. Троллоп, X. Бек, Б.С. Бест и др. М.: Мир, 1983.
49. Ухов С.Б. Скальные основания гидротехнических сооружений. М.: Энергия, 1975.
50. Фадеев А. Б. Метод конечных элементов в геомеханике. М.: Недра, 1987.
51. Цытович Н.А., Кубецкий В.Л., Нгуен Тхе Фунг. Реологические процессы в трещиноватых полускальных породах в режимах нагружения, релаксации и разгрузки. Труды 3-го Всесоюзного симпозиума по реологии грунтов. Ереван: Ереванский ун-т, 1980. С. 354-359.
52. Цытович Н.А., Тер-Мартиросян 3.Г. Основы прикладной геомеханики в строительстве. М.: Высшая школа, 1981.
54. Abelev M.Y., Kubetsky V.L., Tsoi A.V., Meschyan S.R. Investigation of soils creep // Proc. of the 19 Internat. Congress on Soil Mechanics and Foundation Engineering. - Stockholm. - 1981. - P. 523-526.
55. Kubetsky V.L. Rock strength investigation method//Proc. of the I. G. S. Conference „Geocon". - New Delhi. - 1978. - P. 295-299.
59. Kubetsky V.L., Eristov V.S. In situ investigations of creep in rock for the design of pressure tunnel linings//Proc. of the jlnternat Conference on in Situ Investigations in Soil and Rocks. - London. - 1969. - P. 53-61.
61. Tsytovich N.A., Ukhov S.В., Kubetsky V.L. Rock and semirock mechanics as department of applied geomechanics in construction//Proc. of tbe 4 Internat. Congress on Rock Mechanics. Montreux. - 1979. - P. 685-689.
| Расположен в: |
|---|
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/53485
На эту страницу сайта можно сделать ссылку:
На правах рекламы:
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|