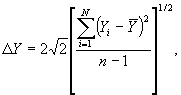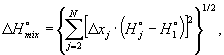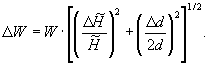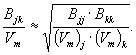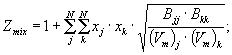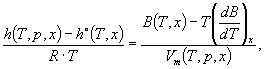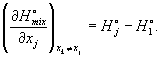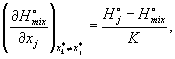
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"ГОСТ 31369-2008 Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности и числа Воббе на основе компонентного состава.
Газ природный ВЫЧИСЛЕНИЕ ТЕПЛОТЫ СГОРАНИЯ, ISO 6976:1995
Предисловие Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-97 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Порядок разработки, принятия, применения, обновления и отмены» Сведения о стандарте 1 ПОДГОТОВЛЕН Открытым акционерным обществом «Газпром» и Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева» (ФГУП «ВНИИМ им. Д.И. Менделеева») на основе собственного аутентичного перевода стандарта, указанного в пункте 4 2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии 3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол № 33 от 06 июня 2008 г.) За принятие стандарта проголосовали:
4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 6976:1995 «Газ природный. Вычисление теплоты сгорания, плотности, относительной плотности и числа Воббе на основе компонентного состава» (ISO 6976:1995 «Natural gas - Calculation of calorific values, density, relative density and Wobbe index from composition»). При этом дополнительные положения в тексте стандарта выделены курсивом, приложения М, N и Р дополняют стандарт с целью учета потребностей национальной экономики указанных выше государств и/или особенностей межгосударственной стандартизации 5 Приказом Федерального агентства по техническому регулированию и метрологии от 17 декабря 2008 г. № 422-ст межгосударственный стандарт ГОСТ 31369-2008 (ИСО 6976:1995) введен в действие в качестве национального стандарта Российской Федерации с 1 января 2010 г. 6 ВВЕДЕН ВПЕРВЫЕ Информация о введении в действие (прекращении действия) настоящего стандарта публикуется в указателе «Национальные стандарты». Информация об изменениях к настоящему стандарту публикуется в указателе «Национальные стандарты», а текст изменений - в информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе «Национальные стандарты» СодержаниеМЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Дата введения - 2010-01-01 1 Область примененияНастоящий стандарт распространяется на физико-химические показатели качества природного газа и устанавливает алгоритмы вычисления значений высшей теплоты сгорания, низшей теплоты сгорания, плотности, относительной плотности и числа Воббе природных газов*, имитаторов природного газа и других горючих газообразных топлив по известному компонентному составу газа при стандартных условиях измерений. * В международном стандарте ИСО 6976 используют термин «сухие природные газы». Определение «сухие» исключено, так как стандарт распространяется на реальные природные газы с содержанием паров воды вплоть до уровня, соответствующего состоянию насыщения. Для вычисления физико-химических показателей качества природного газа используют значения различных физических величин чистых компонентов, приведенные в таблицах 1-5 (раздел 10). В настоящем стандарте приведены методы оценки точности вычисленных значений основных показателей качества природного газа*. * В приложении М приведены требования к точности определения компонентного состава природного газа и расширенная неопределенность для значений теплоты сгорания и плотности. В приложении N приведен алгоритм оценки неопределенности для значений теплоты сгорания, плотности и числа Воббе природного газа. Методы вычисления значений показателей качества на основе молярной доли или массовой концентрации применимы к любому составу природного газа*, имитатора природного газа или другого горючего топлива, которое обычно находится в газообразном состоянии. Для вычисления значений показателей качества газа, состав которого известен в объемных долях, эти методы применимы только для газов, состоящих, в основном, из метана (молярная доля метана не менее 0,5). * В международном стандарте ИСО 6976 используют термин «сухие природные газы». Определение «сухие» исключено, так как стандарт распространяется на реальные природные газы с содержанием паров воды вплоть до уровня, соответствующего состоянию насыщения. Примеры вычислений приведены в приложении D в соответствии с рекомендуемыми методами расчетов. Примечание 1 - Обозначения и единицы измерений физических величин, используемые в настоящем стандарте, приведены в приложении А. Примечание 2 - Слова «верхний (higher)», «верхний (upper)», «полный (total)» и «валовой (gross)» в настоящем стандарте являются синонимами слова «высший (superior)». Аналогично, слова «нижний (lower)» и «чистый (net)» являются синонимами слова «низший (inferior)». Термин «теплотворная способность (heating value)» является синонимом термина «теплота сгорания (calorific value)»; «специфическая плотность (specific gravity)» является синонимом «относительной плотности (relative density)»; «индекс Воббе (Wobbe index)» - синонимом «числа Воббе (Wobbe number)»; «фактор сжатия (compression factor)» - синонимом «коэффициента сжимаемости (compressibility factor)». Примечание 3 - Если состав газа известен в единицах объемной доли, их следует пересчитать в единицы молярной доли (приложение С). Однако следует учитывать, что рассчитанные значения молярной доли будут иметь большие значения неопределенности, чем неопределенности исходных значений объемной доли. Примечание 4 - Сумма значений содержания компонентов в единицах молярной доли не должна отличаться от единицы более чем на 0,0001, и при вычислениях должны учитываться все компоненты, молярная доля которых превышает 0,00005. Примечание 5 - Для вычисления значения объемной теплоты сгорания существуют ограничения по содержанию компонентов в природном газе, помимо метана, а именно: молярная доля азота не должна превышать 0,3; молярная доля СO2 и С2Н6 (каждого) не должна превышать 0,15; молярная доля ни одного другого компонента не должна превышать 0,05. При таких ограничениях ожидаемая систематическая погрешность результата вычисления теплоты сгорания не будет превышать 0,1 %. Примечание 6 - Оценка влияния содержания паров воды, непосредственно измеренного или оцененного путем расчета, на значение теплоты сгорания приведена в приложении F. Примечание 7 - Приведенные методы вычисления действительны для газа, находящегося в принятых стандартных условиях при температуре выше температуры его точки росы. Примечание 8 - Приведенные в таблицах раздела 10 значения физических свойств компонентов периодически пересматриваются с целью их уточнения. 2 Термины и определенияВ настоящем стандарте применены следующие термины с соответствующими определениями: 2.1 высшая теплота сгорания (superior calorific value): Количество теплоты, которое может выделиться при полном сгорании в воздухе определенного количества газа таким образом, что давление p1 при котором происходит реакция, остается постоянным, а все продукты сгорания принимают ту же температуру t1 что и температура реагентов. При этом все продукты находятся в газообразном состоянии, за исключением воды, которая конденсируется в жидкость при t1. В тех случаях, когда теплоту сгорания определяют на основе компонентного состава газа, выраженного в единицах молярной доли, ее обозначают, как В тех случаях, когда теплоту сгорания определяют на основе компонентного состава газа, выраженного в единицах объемной доли, ее обозначают как 2.2 низшая теплота сгорания (inferior calorific value): Количество теплоты, которое может выделиться при полном сгорании в воздухе определенного количества газа таким образом, что давление p1 при котором протекает реакция, остается постоянным, все продукты сгорания принимают ту же температуру t1, что и температура реагентов. При этом все продукты находятся в газообразном состоянии. Рассчитанное на основе единиц молярной доли, массовой доли и объемной доли компонентов
значение низшей теплоты сгорания обозначают, соответственно, как 2.3 плотность (density): Масса газовой пробы, деленная на ее объем при определенных значениях давления и температуры. 2.4 относительная плотность (relative density): Плотность газа, деленная на плотность сухого воздуха стандартного состава (приложение В) при одинаковых заданных значениях давления и температуры. Термин «идеальная относительная плотность» применяют в тех случаях, когда как газ, так и воздух считаются средами, которые подчиняются закону идеального газа (2.7); термин «реальная относительная плотность» применяют в тех случаях, когда как газ, так и воздух считаются реальными средами. 2.5 число Воббе (Wobbe index)*: Значение высшей объемной теплоты сгорания при определенных стандартных условиях, деленное на квадратный корень относительной плотности при тех же стандартных условиях измерений. * Число Воббе - характеристика горючего газа, определяющая взаимозаменяемость горючих газов при сжигании в бытовых и промышленных горелочных устройствах, измеряется в мегаджоулях на кубический метр. 2.6 энтальпия перехода (entalphy of transformation): Энтальпия перехода вещества из состояния А в состояние В является термодинамическим обозначением количества выделяемой теплоты, которое сопровождает переход между состояниями. Положительное выделение теплоты условно считается численно равным отрицательному приращению энтальпии. Исходя из этого, величины энтальпии сгорания и энтальпии испарения имеют численно равные значения. Термин «поправка на энтальпию» относится к (молярной) энтальпии перехода между идеальным и реальным состояниями газа. 2.7 идеальный газ и реальный газ (ideal gas and real gas): Идеальный газ - это газ, который подчиняется закону идеального газа
где р - абсолютное давление; Vm - объем одного моля газа; R - молярная газовая постоянная в когерентных производных единицах; Т - термодинамическая температура. Реальный газ не подчиняется этому закону. Для реальных газов уравнение (1) следует записать в следующем виде
где Z (T, p) - переменная, часто близкая к единице и известная как коэффициент сжимаемости (2.8 и Е.2 (приложение Е)). 2.8 коэффициент сжимаемости (compression factor): Действительный (реальный) объем данной массы газа при определенных давлении и температуре, деленный на его объем при тех же самых условиях, вычисленный по уравнению закона идеального газа. 2.9 стандартные условия сгорания (combustion reference conditions): Определенные температура t1 и давление p1 Они являются условиями, при которых условно сжигают топливо (рисунок 1).
Рисунок 1 - Объемная теплота сгорания. Стандартные условия измерений и сгорания 2.10 стандартные условия измерений (metering reference conditions): Определенные температура t2 и давление р2. Они являются условиями, при которых количество сжигаемого топлива определяется условно, и не существует причины a priori считать условия такими же самыми, как и стандартные условия сгорания (рисунок 1). Примечание 9 - В таблицах 2-5 приведены значения физических величин для компонентов природного газа при разных стандартных условиях измерений*. * Стандартные условия для проведения измерений и расчетов, принятые в разных странах, приведены в приложении Р. 2.11 сухой природный газ (dry natural gas): Газ, в котором молярная доля паров воды не превышает 0,00020* * Приведенное в оригинале значение «0,00005» изменено на «0,00020», так как влияние паров воды с молярной долей менее 0,00020 пренебрежимо мало и не отражается на значении и точности определения параметров природного газа. Примечание - Термин в конкретном толковании применяется только в контексте данного документа. 2.12 расширенная неопределенность (expanded uncertainty): Величина, определяющая интервал вокруг результата измерений, в пределах которого, как можно ожидать, находится большая часть распределения значений, которые с достаточным основанием могли бы быть приписаны измеряемой величине. Примечание - Относительная расширенная неопределенность U0 представляет собой отношение значения расширенной неопределенности U к результату измерений, выраженное в процентах или в долях. 3 Принцип методов вычисленийВ настоящем стандарте приведены методы вычисления значений теплоты сгорания, плотности, относительной плотности и числа Воббе любого природного газа, имитатора природного газа или другого горючего газового топлива, исходя из известного компонентного состава. Свойства газа являются аддитивными; при расчете «суммарного значения» свойства моля идеального природного газа значения термодинамических свойств индивидуальных компонентов берут с весами в соответствии со значениями их молярной доли. Значения теплоты сгорания, рассчитанные на основе значений объемной доли компонентов, затем пересчитывают в значения для реального газа, используя поправочный коэффициент, учитывающий неидеальность газовой смеси (коэффициент сжимаемости смеси). Примечание 10 - Поправочный коэффициент на энтальпию, который, в принципе, необходим при вычислениях значения теплоты сгорания, считается незначительным во всех реальных случаях. В настоящем стандарте методы вычисления значений физико-химических показателей качества горючих газов основаны на результатах определения компонентного состава методом газовой хроматографии, позволяющим измерить содержание всех важных компонентов за исключением воды. Поэтому вычисленное значение свойств газа относится к сухому газу. При значении молярной доли водяных паров, превышающем 0,00020, в значения показателей качества сухого газа должна быть внесена поправка в соответствии с рекомендациями приложения F. В разделе 10 приведены значения физических свойств чистых компонентов природного газа, полученные на основе значений молярной доли, массовой доли и объемной доли для обычно используемых стандартных условий. Примеры вычислений приведены в приложении D. 4 Поведение идеальных и реальных газов4.1 Энтальпия сгоранияНаиболее важными фундаментальными физическими величинами, необходимыми при вычислении значений теплоты сгорания, исходя из принципа, положенного в основу метода, являются (стандартные) молярные энтальпии сгорания для идеальных газов - компонентов смеси. Эти величины являются сложными функциями температуры; следовательно, необходимые значения зависят от стандартной температуры сгорания t1. По практическим соображениям предполагается, что сам пользователь не выполняет расчеты, которые дают соответствующие значения молярной энтальпии сгорания при любой произвольной стандартной температуре. Вместо этого приводятся таблицы для температуры t1 =25°С, 20°С, 15°С и 0°С. В разделе Е.1 (приложение Е) рассматриваются методы получения табличных значений; важно отметить, что все 4 значения для любого вещества термодинамически взаимосвязаны. Для значения теплоты сгорания, рассчитанного по любому из трех возможных вариантов, в принципе, требуется так называемая энтальпийная поправка для того, чтобы пересчитать энтальпию идеального газа при сгорании газовой смеси в значение, соответствующее реальному газу. Однако она обычно настолько мала, что ею можно пренебречь. Обоснование, подтверждающее это, приведено в разделе Е.3 (приложение Е). 4.2 Вычисление коэффициента сжимаемостиДля значения объемной теплоты сгорания требуется вторая поправка, учитывающая отличие объема моля реального газа от объема моля идеального газа, этой поправкой пренебрегать нельзя. Она требуется также при вычислении значений плотности, относительной плотности и числа Воббе. В разделе Е.2 (приложение Е) приведено обоснование способа введения поправок на объем, обусловленных неидеальностью газа, рассматриваются принципы их введения и применяемые упрощения, которые дают возможность выполнить вычисления без применения компьютерных программ. Такие поправки на объем, обусловленные неидеальностью газа, вводят с помощью коэффициента сжимаемости Zmix. Коэффициент сжимаемости Zmix для стандартных условий измерений, рассматриваемых в разделах 5-9, рассчитывают по следующей формуле (или по формуле (Е.17) приложение Е) где суммирование проводят по всем N компонентам смеси. Значения так называемого коэффициента
суммирования 5 Вычисление молярной теплоты сгорания5.1 Идеальный газЗначение молярной теплоты сгорания идеального газа, определяемое исходя из значений молярной доли компонентов смеси известного состава, при температуре t1 вычисляют по формуле
где
хj - молярная доля j-го компонента;
Числовые значения Значения Примечание 11 - Значения Примечание 12 - Значение молярной теплоты сгорания идеального газа или газовой смеси определяется в настоящем стандарте как положительное число. Значения, приведенные в таблице 3, численно равны значениям стандартных молярных энтальпий сгорания, которые обычно выражают в виде отрицательных величин (2.6). 5.2 Реальный газВ настоящем стандарте значение молярной теплоты сгорания реального газа принимается численно равным соответствующему значению теплоты сгорания для идеального газа. Примечание 13 - Строгий подход к вычислению молярной теплоты сгорания реального газа, исходя из значения теплоты сгорания идеального газа, может потребовать вычисления поправки на энтальпию (4.1) для смеси. На практике эта поправка для типичных природных газов очень мала и ею можно пренебречь с погрешностью, не превышающей 50 Дж·моль-1 (примерно 0,005 %), раздел Е.3 (приложение Е). 6 Вычисление массовой теплоты сгорания6.1 Идеальный газЗначение массовой теплоты сгорания идеального газа, определяемое исходя из значений массовой доли компонентов смеси известного состава, при температуре t1 вычисляют по формуле где
М - молярная масса смеси, которую вычисляют по формуле где xj - молярная доля j-го компонента; Mj - молярная масса j-го компонента. В таблице 1 (раздел 10) приведены значения молярной массы для всех компонентов, рассматриваемых в настоящем стандарте. Применение формул (5) и (6) является основным способом вычисления где
Для удобства значениям Числовые значения, полученные по любому из этих методов, будут иметь расхождение не более 0,01 МДж·кг -1, которое соответствует точности современного уровня техники. 6.2 Реальный газВ настоящем стандарте значение массовой теплоты сгорания реального газа считается численно равным соответствующему значению теплоты сгорания для идеального газа. Примечание 14 - Объяснение и обоснование - см. 5.2. 7 Вычисление объемной теплоты сгорания7.1 Идеальный газЗначение теплоты сгорания идеального газа, рассчитанное на основе значений объемной доли компонентов, для температуры сгорания t1 смеси известного состава, измеренных при температуре t2 и давлении р2, вычисляют по формуле где
R - универсальная газовая постоянная (равная 8,314510 Дж·моль-1·К-1, раздел В.1 (приложение В); Т2 = (t2 + 273,15) - абсолютная температура, К. Формула (8) представляет собой метод вычисления объемной теплоты сгорания где
Для удобства значения Числовые значения, полученные любым из этих методов, будут иметь расхождение не более 0,01 МДж·кг-1, которое соответствует точности современного уровня техники. 7.2 Реальный газЗначение объемной теплоты сгорания газа для температуры сгорания t1 смеси известного состава, объемная доля компонентов которой измерена при температуре t2 и давлении р2, вычисляют по формуле где
Zmix (t2, p2) - коэффициент сжимаемости смеси при стандартных условиях измерений. Коэффициент сжимаемости Zmix(t2, p2) вычисляют по формуле (3) с использованием значений коэффициентов суммирования Примечание 15 - См. 5.2 для пояснения и обоснования практического подхода к вычислениям значений теплоты сгорания реального газа. Поскольку поправка на энтальпию в значение объемной теплоты сгорания реального газа при этом вычислении не вводится, то стандартное давление сгорания p1 не относится к данному случаю, и оно исключается из принятой номенклатуры. 8 Вычисление плотности, относительной плотности и числа Воббе8.1 Идеальный газОтносительная плотность идеального газа не зависит от выбора стандартного состояния, и ее вычисляют по формуле где d° - относительная плотность идеального газа; Mj - молярная масса j-го компонента; Mair - молярная масса сухого воздуха стандартного состава. В таблице 1 (раздел 10) приведены значения молярной массы компонентов природного газа. В разделе В.3 (приложение В) приведен состав стандартного воздуха; рассчитанное значение Mair равно 28,9626 кг·кмоль-1. Плотность идеального газа зависит от его температуры t и давления р, и ее вычисляют по формуле где ρ° (t, p) - плотность идеального газа; R - универсальная газовая постоянная, равная 8,314510 Дж·моль-1·К-1, раздел В.1 (приложение В); T = (t + 273,15) - абсолютная температура, К. Число Воббе идеального газа вычисляют по формуле где W° - число Воббе идеального газа;
8.2 Реальный газОтносительную плотность реального газа вычисляют по формуле где d (t, р) - относительная плотность реального газа; Zair (t, p) - коэффициент сжимаемости сухого воздуха стандартного состава; Zmix (t, p) - коэффициент сжимаемости газа. Коэффициент сжимаемости Zmix(t, p) вычисляют по формуле (3), с использованием значений коэффициентов суммирования Zair (273,15 К, 101,325 кПа) = 0,99941; Zair (288,15 К, 101,325 кПа) = 0,99958; Zair (293,15 К, 101,325 кПа) = 0,99963. Плотность реального газа вычисляют по формуле где ρ (t, p) - плотность реального газа. Число Воббе реального газа вычисляют по формуле где W - число Воббе реального газа;
Примечание 16 - Требуется определенная внимательность при применении единиц измерения при вычислениях, приведенных в настоящем подразделе, особенно при вычислениях плотности. При R, выраженной в джоулях на моль-кельвин, р - в килопаскалях и М - в килограммах на киломоль, значение ρ автоматически получается в килограммах на кубический метр - это рекомендуемая единица СИ. 9 Точность9.1 Прецизионность9.1.1 Сходимость и воспроизводимость Прецизионность вычисленного значения физического свойства, которая является результатом только случайных погрешностей анализа, может быть выражена в терминах сходимости и/или воспроизводимости. Сходимость - значение, ниже которого с определенной доверительной вероятностью находится абсолютная разность между двумя последовательными результатами испытаний, полученными одним и тем же методом на идентичном испытуемом материале одним и тем же оператором с применением одного и того же оборудования в одной и той же лаборатории в пределах короткого промежутка времени. При отсутствии других указаний доверительная вероятность равна 95 %. Воспроизводимость - значение, ниже которого с определенной доверительной вероятностью находится абсолютная разность между двумя одиночными результатами испытаний, полученными одним и тем же методом на идентичном испытуемом материале различными операторами с использованием различного оборудования в разных лабораториях. При отсутствии других указаний доверительная вероятность равна 95 %. Значение второго показателя обычно значительно больше, чем первого. Каждая оценка прецизионности вычисленного значения физического свойства зависит только от прецизионности аналитических данных. Общие понятия сходимости и воспроизводимости можно применять не только к физическим свойствам, вычисляемым по результатам определения состава, но также и к содержанию каждого компонента, определенного при анализе, на основе которого получают эти свойства. Следовательно, оценки сходимости или воспроизводимости значения физического свойства можно получить одним из двух очевидно эквивалентных способов, а именно: a) с помощью прямого применения приведенных выше определений к повторным вычислениям исследуемого физического свойства, т.е. по формуле где DY - оценка сходимости или воспроизводимости Y; Yi - значение физического свойства, вычисленное по результатам i-го анализа газа;
Примечание 17 - В отношении определений сходимости и воспроизводимости, их интерпретации в терминах стандартного отклонения совокупности значений, задаваемых формулой (17), и в отношении происхождения коэффициента b) объединяя определенным образом оценки сходимости или воспроизводимости содержания каждого компонента, измеренного при анализе газа, соответствующие формулы объединения приведены в 9.1.2 и 9.1.3 (вывод этих формул - см. приложение Н). Примечание 18 - На практике эквивалентность предложенных способов а) и b) открыта для обсуждения. Причина в том, что статистическая связь между методами предполагает, что повторно полученные результаты анализа имеют гауссовское (нормальное) распределение для содержания каждого компонента и что это также верно для набора вычисленных значений физических свойств. Опыт показал, что эти критерии обычно не выполняются, особенно для малых наборов данных и/или наборов, содержащих выбросы. 9.1.2 Оценка сходимости Сходимость DН значения теплоты сгорания Н при 95 %-ном доверительном уровне можно вычислить по формуле (17) (заменив Y на Н) или прямо по данным анализа, применяя соответствующие формулы: а) если проанализированы все компоненты, за исключением метана (j = 1), а его содержание вычисляют по разности, то где
Dхj - оценка сходимости молярной доли j-го компонента в смеси из N компонентов;
b) если проанализированы все компоненты, включая метан, то где, несмотря на то, что Оценку сходимости Dd относительной плотности и Dρ плотности можно вычислить по следующим формулам, соответственно:
где DM - оценка сходимости определения средней молярной массы М природного газа, которую вычисляют по формулам: - для случая а) - для случая b) где Mj - молярная масса j-го компонента. Оценку сходимости DW числа Воббе можно вычислить по формуле Как и для значения теплоты сгорания, оценки сходимости DM, Dd, Dρ и DW можно также определить с помощью вычисления стандартного отклонения набора вычисленных значений свойства [т.е. по формуле (17), заменив Y на М, d, ρ и W, соответственно], если анализы состава были выполнены в соответствии с определением сходимости, приведенным в 9.1.1. Однако при этом все-таки учитывают примечание 18 к 9.1.1. Примечание 19 - Вклад сходимости DZ вычисленного коэффициента сжимаемости Z в общую сходимость 9.1.3 Оценка воспроизводимости Оценки воспроизводимости DН, Dd, Dρ и DW значений теплоты сгорания, относительной плотности, плотности и числа Воббе можно вычислить по формулам (18)-(24) при условии, что Dxj и 9.2 ПравильностьОценки прецизионности аналитических данных не могут рассматриваться как имеющие какое-либо значение для оценки правильности этих данных; вполне возможно при высокой прецизионности получение неправильных данных. Правильность вычисленного значения показателя качества природного газа может рассматриваться как комбинация трех независимых источников систематической погрешности, а именно: a) неопределенностей табличных данных, приведенных в таблицах 1-5; b) систематической погрешности метода вычисления, в котором используются эти данные; c) неопределенностей (в отличие от прецизионности) аналитических данных, используемых при вычислениях. На практике трудно получить численные оценки правильности из-за недостатка адекватной информации; например, обращение к оригинальным источникам табличных данных часто позволяет обнаружить информацию, касающуюся только прецизионности (см. в этом контексте обсуждение метана, приведенное в приложении G), и то же самое часто верно для аналитических данных. Кроме того, строгий подход мог бы дать оценку абсолютного значения неопределенности, тогда как на практике часто требуется оценка неопределенности значения показателя качества относительно некоторой выбранной точки. Например, значения теплоты сгорания часто сравнивают со значением теплоты сгорания чистого метана. В этом случае неопределенность принятого значения теплоты сгорания метана не дает вклада в неопределенность значения теплоты сгорания природного газа или в разность между значениями теплоты сгорания двух различных природных газов. Опыт показал, что на относительные неопределенности значений рассматриваемых здесь физических свойств больше всего будут влиять неопределенности аналитических данных и что вклады от неопределенностей табличных данных и систематической погрешности метода вычисления будут очень малы. Ожидается, что вклады от табличных данных будут менее 0,05 %, а от смещения метода вычисления будут менее 0,015 %. Этими вкладами можно пренебречь по сравнению с неопределенностью аналитических данных, полученных при анализе типичной смеси природного газа, содержащей от 12 до 20 компонентов. В тех случаях, когда вклады от неопределенностей табличных данных и от смещения метода вычисления являются значимыми по сравнению с аналитической неопределенностью (например для высокоточного анализа смесей только малого числа компонентов и, возможно, в будущем, после улучшения точности анализа природного газа), может потребоваться более строгий подход, основанный на более точной оценке источников систематической погрешности, перечисленных в а), b) и с). 9.3 Представление результатовЧисло значащих цифр, которое следует приводить для значения каждого показателя качества природного газа, должно отражать ожидаемую точность вычисления определяемого показателя. Даже в случае «совершенного» анализа результат вычислений для смесей не следует записывать с числом значащих цифр после запятой, превышающим: значение молярной теплоты сгорания - 0,01 кДж·моль-1 значение массовой теплоты сгорания - 0,01 МДж·кг-1 значение объемной теплоты сгорания - 0,01 МДж·м-3 относительную плотность - 0,0001 плотность - 0,0001 кг·м-3 число Воббе - 0,01 МДж·м-3. Необходимо, однако, обратить внимание на то, действительно ли аналитические данные подтверждают возможность записи результата в установленных единицах с таким числом значащих цифр после запятой, и, если нет, следует соответственно уменьшить их число. 10 Таблицы рекомендуемых данныхТаблица 1 - Молярные массы компонентов природного газа
Таблица 2 - Коэффициенты сжимаемости и коэффициенты суммирования для компонентов природного газа для различных стандартных условий измерений Все значения, за исключением коэффициентов суммирования для водорода, гелия (пересчитаны) и неона (оценены), взяты из [3].
Таблица 3 - Значения молярной теплоты сгорания компонентов природных газов при различных стандартных условиях сгорания для идеального газа Все значения
Таблица 4 - Значения массовой теплоты сгорания компонентов природного газа при различных стандартных условиях сгорания для идеального газа Все значения были получены делением соответствующего значения
Таблица 5 - Значения объемной теплоты сгорания компонентов природного газа при различных стандартных условиях сгорания и измерений для идеального газа Все значения были получены умножением соответствующего значения
Приложение А
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
R = (8,314510 ± 0,000070) Дж·моль-1·К-1. |
(В.1) |
В.2 Критические константы и коэффициент ацентричности
В таблице В.1 приведены выборочные значения критической температуры Тс, критического давления рс и коэффициента ацентричности ω, которые использовались для получения с помощью формулы Питцера-Керла, раздел Е.2 (приложение Е), значений коэффициентов сжимаемости Z, приведенных в таблице 2. Все значения взяты из [3].
В.3 Свойства сухого воздуха
Рекомендуемый молярный состав сухого воздуха приведен в таблице В.2. Количественный состав определен в работах [5], [6] и такой же как в [3]. Отметим, что во многих других альтернативных источниках, включая [7], приведен объемный состав воздуха, а не молярный; последний больше подходит для прямого вычисления средней молярной массы (молекулярной массы).
Значение молярной массы сухого воздуха, округленное до четвертого десятичного знака, равно
|
Mair = 28,9626 кг·кмоль-1. |
(В.2) |
Значения коэффициентов сжимаемости сухого воздуха стандартного состава при каждом из трех обычно применяемых стандартных условий измерений следует принимать по [3] следующими:
|
Zair (273,15 К, 101,325 кПа) = 0,99941; |
(В.3) |
|
Zair (288,15 К, 101,325 кПа) = 0,99958; |
(В.4) |
|
Zair (293,15 К, 101,325 кПа) = 0,99963. |
(В.5) |
Плотность реального воздуха стандартного состава с учетом этих значений возрастает и равна:
|
ρair (273,15 К, 101,325 кПа) = 1,292923 кг·м-3; |
(В.6) |
|
ρair (288,15 К, 101,325 кПа) = 1,225410 кг·м-3; |
(В.7) |
|
ρair (293,15 К, 101,325 кПа) = 1,204449 кг·м-3. |
(В.8) |
В.4 Энтальпия испарения воды
Стандартная молярная энтальпия испарения воды необходима при каждом из четырех обычно применяемых стандартных условий сгорания для того, чтобы облегчить вычисления разности между значением высшей теплоты сгорания идеального газа и значением низшей теплоты сгорания (на основе значений молярной доли) для каждого компонента. При расчете значений низшей теплоты сгорания, приведенных в таблице 3, использовались следующие значения по [3]:
|
L° (273,15 К) = 45,074 кДж·моль-1; |
(В.9) |
|
L° (288,15 К) = 44,433 кДж·моль-1; |
(В.10) |
|
L° (293,15 К) = 44,224 кДж·моль-1; |
(В.11) |
|
L° (298,15 К) = 44,016 кДж·моль-1. |
(В.12) |
Таблица В.1 - Критические параметры
|
Компонент |
Критическая температура, К |
Критическое давление, кПа |
Коэффициент ацентричности |
|
1 Метан |
190,555 |
4598,8 |
0,0115 |
|
2 Этан |
305,83 |
4880 |
0,0908 |
|
3 Пропан |
369,82 |
4250 |
0,1454 |
|
4 н-Бутан |
425,14 |
3784 |
0,1928 |
|
5 2-Метилпропан |
408,13 |
3648 |
0,1756 |
|
6 н-Пентан |
469,69 |
3364 |
0,2510 |
|
7 2-Метилбутан |
460,39 |
3381 |
0,2273 |
|
8 2,2-Диметилпропан |
433,75 |
3199 |
0,1970 |
|
9 н-Гексан |
506,4 |
3030 |
0,2957 |
|
10 2-Метилпентан |
497,5 |
3010 |
0,2791 |
|
11 3-Метилпентан |
504,4 |
3120 |
0,2750 |
|
12 2,2-Диметилбутан |
488,7 |
3080 |
0,2310 |
|
13 2,3-Диметилбутан |
499,9 |
3130 |
0,2473 |
|
14 н-Гептан |
539,2 |
2740 |
0,3506 |
|
15 н-Октан |
568,4 |
2490 |
0,3942 |
|
16 н-Нонан |
594,4 |
2280 |
0,4437 |
|
17 н-Декан |
617,8 |
2090 |
0,4902 |
|
|
|
|
|
|
18 Этилен |
282,35 |
5042 |
0,0856 |
|
19 Пропилен |
364,85 |
4601 |
0,1477 |
|
20 1-Бутен |
419,53 |
4023 |
0,1874 |
|
21 цис-2-Бутен |
435,58 |
4220 |
0,2044 |
|
22 транс-2-Бутен |
428,63 |
4050 |
0,2138 |
|
23 2-Метилпропен |
417,90 |
4000 |
0,1898 |
|
24 1-Пентен |
464,78 |
3526 |
0,2450 |
|
|
|
|
|
|
25 Пропадиен |
393 |
5470 |
0,149 |
|
26 1,2-Бутадиен |
443,7 |
4500 |
0,3394 |
|
27 1,3-Бутадиен |
425 |
4330 |
0,1814 |
|
|
|
|
|
|
28 Ацетилен |
308,33 |
6139 |
0,1841 |
|
|
|
|
|
|
29 Циклопентан |
511,61 |
4502 |
0,1923 |
|
30 Метилциклопентан |
532,73 |
3784 |
0,2395 |
|
31 Этилциклопентан |
569,46 |
3397 |
0,2826 |
|
32 Циклогексан |
553,5 |
4074 |
0,2144 |
|
33 Метилциклогексан |
572,12 |
3471 |
0,2333 |
|
34 Этилциклогексан |
609 |
3040 |
0,2426 |
|
35 Бензол |
562,16 |
4898 |
0,2100 |
|
36 Толуол |
591,80 |
4106 |
0,2566 |
|
37 Этилбензол |
617,20 |
3606 |
0,3011 |
|
38 о-Ксилол |
630,33 |
3734 |
0,3136 |
|
|
|
|
|
|
39 Метанол |
512,64 |
8092 |
0,556 |
|
40 Метантиол |
470,0 |
7230 |
0,153 |
|
|
|
|
|
|
41 Водород |
33,2 |
1297 |
-0,218 |
|
42 Вода |
647,14 |
22064 |
0,328 |
|
43 Сульфид водорода |
373,2 |
8940 |
0,109 |
|
44 Аммиак |
405,5 |
11350 |
0,250 |
|
45 Цианид водорода |
456,7 |
5390 |
0,388 |
|
46 Монооксид углерода |
132,85 |
3494 |
0,053 |
|
47 Карбонил сульфид |
378,8 |
6349 |
0,096 |
|
48 Дисульфид углерода |
552 |
7900 |
0,109 |
|
|
|
|
|
|
49 Гелий |
5,19 |
227 |
-0,365 |
|
50 Неон |
44,40 |
2760 |
-0,029 |
|
51 Аргон |
150,65 |
4866 |
0,001 |
|
52 Азот |
126,2 |
3390 |
0,039 |
|
53 Кислород |
154,58 |
5043 |
0,025 |
|
54 Диоксид углерода |
304,20 |
7386 |
0,239 |
|
55 Диоксид серы |
430,8 |
7884 |
0,256 |
Таблица В.2 - Молярный состав сухого воздуха
|
Компонент |
Молярная доля |
|
Азот |
0,781 02 |
|
Кислород |
0,209 46 |
|
Аргон |
0,009 16 |
|
Диоксид углерода |
0,000 33 |
|
Неон |
0,000 018 2 |
|
Гелий |
0,000 005 2 |
|
Метан |
0,000 001 5 |
|
Криптон |
0,000 001 1 |
|
Водород |
0,000 000 5 |
|
Монооксид диазота |
0,000 000 3 |
|
Монооксид углерода |
0,000 000 2 |
|
Ксенон |
0,000 000 1 |
Приложение С
(справочное)
Пересчет значения объемной доли в значение молярной доли
Если состав газа известен в значениях объемной доли при стандартных условиях измерений (t2, p2), то пересчет в значения молярной доли можно провести по формуле
|
|
(С.1) |
для всех j.
Приложение D
(справочное)
Примеры вычислений
В таблице D.1 приведен пример, представленный в простом табличном виде, вычислений значений относительной молярной массы, высшей идеальной молярной теплоты сгорания и коэффициента сжимаемости природного газа конкретного состава по данным основных физических свойств для стандартных условий «15/15°С» (стандартные условия ИСО). В приведенных вычислениях числовые значения всех используемых величин были округлены до пяти значащих цифр и в таком виде использовались во всех последующих вычислениях. В действительности, все вычисления следует выполнять, используя все доступные на калькуляторе или компьютере цифры, проводя округление только на последнем этапе, чтобы правильно представить результат с соответствующим числом значащих цифр (9.3). Другие физические свойства природного газа вычисляют в соответствии с методами, описанными в настоящем стандарте, следующим образом.
Примечание 20 - Полная процедура вычислений значения теплоты сгорания, приведенная в настоящем приложении, относится только к значению высшей теплоты сгорания. Вычисление значения низшей теплоты сгорания проводят аналогичным способом.
D.1 Молярная теплота сгорания (раздел 5)
Из таблице D.1 видно, что значение высшей теплоты сгорания на основе значений молярной доли компонентов ![]() идеального газа при 15°С после округления равно 919,09 кДж·моль-1.
идеального газа при 15°С после округления равно 919,09 кДж·моль-1.
Оно также принимается как значение ![]() теплоты сгорания реального газа, так как поправка на энтальпию при
переходе от идеального на реальный газ является достаточно маленькой, чтобы ею можно было пренебречь (примечание 13 к 5.2).
теплоты сгорания реального газа, так как поправка на энтальпию при
переходе от идеального на реальный газ является достаточно маленькой, чтобы ею можно было пренебречь (примечание 13 к 5.2).
D.2 Массовая теплота сгорания (раздел 6)
В соответствии с разделом 6 значение высшей массовой теплоты сгорания ![]() идеального газа вычисляют по
формуле (5)
идеального газа вычисляют по
формуле (5)
|
|
(D.1) |
где
из таблицы D.1:
![]() (15°C) = 919,09 кДж·моль-1;
(15°C) = 919,09 кДж·моль-1;
М = 17,478 кг·кмоль-1.
Таким образом,
![]() ,
,
результат представляют как 52,59 МДж·кг-1.
![]() также можно вычислить по формуле (7)
также можно вычислить по формуле (7)
|
|
(D.2) |
Это вычисление также дает значение теплоты сгорания 52,59 МДж·кг-1.
D.3 Объемная теплота сгорания (раздел 7)
В соответствии с 7.1 значение высшей объемной теплоты сгорания идеального газа ![]() вычисляют по формуле (8)
вычисляют по формуле (8)
|
|
(D.3) |
где
из таблицы D.1:
![]() (15°С) = 919,09 кДж·моль-1;
(15°С) = 919,09 кДж·моль-1;
р2 = 101,325 кПа;
Т2 = 288,15 К;
R = 8,314510 Дж·моль-1·K-1 - универсальная газовая постоянная.
Таким образом:
![]()
и результат представляют как 38,87 МДж·м-3.
![]() также можно вычислить по формуле (9)
также можно вычислить по формуле (9)
|
|
(D.4) |
которая также дает значение 38,87 МДж·м-3.
При переходе от идеального к реальному газу вычисления проводят в соответствии с методикой, описанной в 7.2
|
|
(D.5) |
где
Zmix - коэффициент сжимаемости газовой смеси, вычисляемый по формуле (3)
|
|
(D.6) |
Из таблицы D.1 видно, что значение суммы коэффициентов суммирования молярных долей равно 0,04785, следовательно,
Zmix(15°C, 101,325 кПа) = 1 - (0,04785)2 = 0,99771, записывается как 0,9977, и значение высшей теплоты сгорания реального газа равно
![]()
результат представляют как 38,96 МДж·м-3.
D.4 Относительная плотность, плотность и число Воббе (раздел 8)
D.4.1 Относительная плотность
В соответствии с 8.1 относительную плотность идеального газа вычисляют по формуле (11)
|
|
(D.7) |
Используя данные из таблицы D.1 и значение Мair = 28,9626 кг·кмоль-1, получают
![]()
результат представляют как 0,6035.
В соответствии с 8.2 относительную плотность реального газа вычисляют по формуле (14)
|
|
(D.8) |
где
Zair(15°C, 101,325 кПа) равен 0,99958 (см. таблицу 2);
Zmix равен 0,99771 (раздел D.3).
Таким образом,
![]()
результат представляют как 0,6046.
D.4.2 Плотность
В соответствии с 8.1 плотность идеального газа вычисляют по формуле (12)
|
|
(D.9) |
Таким образом,
![]()
результат представляют как 0,7392 кг·м-3.
Согласно 8.2 плотность реального газа вычисляют по формуле (15)
![]()
Таким образом,
![]()
результат представляют как 0,7409 кг·м-3.
D.4.3 Число Воббе
В соответствии с 8.1 число Воббе для идеального газа вычисляют по формуле (13)
|
|
(D.10) |
Таким образом,
![]()
результат представляют как 50,04 МДж·м-3.
Согласно 8.2 число Воббе для реального газа вычисляют по формуле (16)
|
|
(D.11) |
Таким образом,
![]()
результат представляют как 50,10 МДж·м-3.
Отметим, что все значения, вычисленные в настоящем приложении, идентичны значениям, которые дает компьютерная программа, описанная в приложении К, за исключением значения W. Однако если полное число цифр сохраняют без округления во всех вычислениях в примере, касающемся расчета значения W, то получают правильное значение 50,11 МДж·м-3, как в приложении К.
D.5 Прецизионность (раздел 9)
В таблице D.2 приведен пример вычислений сходимости, представленный в формате, аналогичном таблице D.1 для такой же газовой смеси. Рассматривается случай, когда содержание метана измеряется (а не вычисляется по разности). Для выполнения этих вычислений необходимо знать оценку сходимости ненормализованных
значений молярной доли каждого индивидуального компонента. Используемые значения приведены в таблице D.2, графа «Сходимость ненормализованной молярной доли ![]() ».
».
D.5.1 Сходимость результатов измерений молярной теплоты сгорания
Из таблицы D.2 для значения высшей теплоты сгорания идеального газа 919,09 кДж·моль-3 сходимость ![]() равна ±0,11 кДж·моль-1 [см. формулу (19)].
равна ±0,11 кДж·моль-1 [см. формулу (19)].
D.5.2 Сходимость результатов измерений массовой теплоты сгорания
Чтобы получить оценку сходимости для идеального газа (на основе значений массовой концентрации компонентов), сходимость, рассчитанную на основе молярной доли, делят на значение молярной массы газа 17,478 кг·кмоль-1.
![]()
результат представляют как ±0,01 МДж·кг-1.
Оценка сходимости для значения высшей теплоты сгорания 52,59 МДж·кг-1, рассчитанная на основе значений массовой доли компонентов, равна ±0,01 МДж·кг-1.
D.5.3 Сходимость результатов измерений объемной теплоты сгорания
Чтобы получить оценку сходимости для идеального газа (на основе значений объемной доли компонентов), сходимость, рассчитанную на основе молярной доли, умножают на р2/(R·Т2).
![]() ,
,
результат представляют как ±0,01 МДж·м-3
Оценка сходимости для значения высшей теплоты сгорания идеального газа 38,87 МДж·м-3, рассчитанной на основе значений объемной доли компонентов, равна ±0,01 МДж·м-3.
D.5.4 Сходимость относительной плотности, плотности и числа Воббе
D.5.4.1 Относительная плотность
Оценку сходимости результатов измерений относительной плотности (идеального или реального газа) вычисляют по формуле (20)
![]()
где DМ из таблицы D.2 [см. формулу (23)] равно ±0,0031 кг·моль-1;
Mair = равна 28,9626 кг·кмоль-1.
Таким образом,
![]()
результат представляют как ±0,0001.
Сходимость результатов измерений для относительной плотности идеального газа 0,6035 и относительной плотности реального газа 0,6046 равна ±0,0001.
D.5.4.2 Плотность
Оценку сходимости результатов измерений плотности (идеального или реального газа) вычисляют по формуле (21)
![]()
результат представляют как ±0,0001 кг/м-3.
Сходимость результатов измерений для плотности идеального газа 0,7392 кг·м-3 и плотности реального газа 0,7409 кг·м-3 равна ±0,0001 кг·м-3.
D.5.4.3 Число Воббе
Оценку сходимости результатов измерений числа Воббе для идеального газа вычисляют по формуле (24)
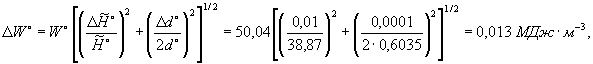
результат представляют как ±0,01 МДж·м-3.
Сходимость результатов измерений для числа Воббе идеального газа 50,04 МДж·м-3 равна ±0,01 МДж·м-3.
Таблица D.1 - Примеры вычисления свойства
|
Компонент |
Молярная
масса Mj, |
Значение
высшей теплоты сгорания |
Коэффициент
суммирования |
Молярная доля xj |
Молярная
доля×молярная масса на моль xj·Mj |
Молярная
доля×значение теплоты сгорания |
Молярная доля× |
|
Метан |
16,043 |
891,56 |
0,0447 |
0,9247 |
14,8350 |
824,43 |
0,04133 |
|
Этан |
30,070 |
1562,14 |
0,0922 |
0,0350 |
1,0525 |
54,67 |
0,00323 |
|
Пропан |
44,097 |
2221,10 |
0,1338 |
0,0098 |
0,4322 |
21,77 |
0,00131 |
|
н-Бутан |
58,123 |
2879,76 |
0,1871 |
0,0022 |
0,1279 |
6,34 |
0,00041 |
|
2-Метилпропан |
58,123 |
2870,58 |
0,1789 |
0,0034 |
0,1976 |
9,76 |
0,00061 |
|
н-Пентан |
72,150 |
3538,60 |
0,2510 |
0,0006 |
0,0433 |
2,12 |
0,00015 |
|
Азот |
28,0135 |
0 |
0,0173 |
0,0175 |
0,4902 |
0 |
0,00030 |
|
Диоксид углерода |
44,010 |
0 |
0,0748 |
0,0068 |
0,2993 |
0 |
0,00051 |
|
Общие |
|
1,0000 |
17,478 |
919,09 |
0,04785 |
||
Таблица D.2 - Примеры вычисления оценки прецизионности
|
Компонент |
Молярная
масса Mj, |
Значение
высшей теплоты сгорания |
Молярная доля xj |
Сходимость
ненормали- |
|
|
|
Метан |
16,043 |
891,56 |
0,9247 |
0,001532 |
0,001779 |
0,00000483 |
|
Этан |
30,070 |
1562,14 |
0,0350 |
0,000086 |
0,003058 |
0,00000117 |
|
Пропан |
44,097 |
2221,10 |
0,0098 |
0,000032 |
0,001736 |
0,00000073 |
|
н-Бутан |
58,123 |
2879,76 |
0,0022 |
0,000010 |
0,000384 |
0,00000017 |
|
2-Метилпропан |
58,123 |
2870,58 |
0,0034 |
0,000006 |
0,000137 |
0,00000006 |
|
н-Пентан |
72,150 |
3538,60 |
0,0006 |
0,000004 |
0,000110 |
0,00000005 |
|
Азот |
28,0135 |
0 |
0,01750 |
0,000064 |
0,003460 |
0,00000045 |
|
Диоксид |
44,010 |
0 |
0,0068 |
0,000052 |
0,002284 |
0,00000190 |
|
Сумма |
1,0000 |
|
0,012948 |
0,00000936 |
||
|
Корень квадратный из суммы |
0,1138 |
0,00306 |
||||
Приложение Е
(справочное)
Поведение идеального и реального газов
Е.1 Изменение энтальпии сгорания идеального газа при изменении температуры
В 4.1 указано, что (стандартная) энтальпия сгорания (![]() ) любого идеального газа или смеси изменяется в
соответствии с температурой, при которой, как полагают, происходит сгорание (т.е. со стандартной температурой
сгорания). Наблюдаемое изменение, хотя и относительно мало, но является значимым и им не следует пренебрегать. Однако это изменение, в общем, является сложным и, как следствие, не имеет смысла представлять способы
вычисления, которые могли бы дать возможность пользователю определять
) любого идеального газа или смеси изменяется в
соответствии с температурой, при которой, как полагают, происходит сгорание (т.е. со стандартной температурой
сгорания). Наблюдаемое изменение, хотя и относительно мало, но является значимым и им не следует пренебрегать. Однако это изменение, в общем, является сложным и, как следствие, не имеет смысла представлять способы
вычисления, которые могли бы дать возможность пользователю определять ![]() при любой произвольной стандартной температуре сгорания. Вместо этого значения
при любой произвольной стандартной температуре сгорания. Вместо этого значения ![]() для каждого отдельного химического компонента, перечисленного в настоящем стандарте, приведены в таблице 3 настоящего стандарта для каждой из обычно
применяемых стандартных температур сгорания: 298,15 К, 293,15 К, 288,15 К и 273,15 К (25°С, 20°С, 15°С и 0°С соответственно).
для каждого отдельного химического компонента, перечисленного в настоящем стандарте, приведены в таблице 3 настоящего стандарта для каждой из обычно
применяемых стандартных температур сгорания: 298,15 К, 293,15 К, 288,15 К и 273,15 К (25°С, 20°С, 15°С и 0°С соответственно).
Приведенные в таблице 3 значения были получены следующим образом. Рассмотрим обобщенную реакцию сгорания для чистого, предположительно газообразного химического компонента (CaHbOcNdSe), в котором числа атомов от a до е являются положительными целыми числами (включая ноль), значения которых определяют конкретный исследуемый компонент (например, для а = 1, b = 4, с = d = е = 0, означающий метан), а именно:
|
|
(E.1) |
Допустим, что информация о стандартной энтальпии сгорания при 25°С [![]() ] для этой реакции имеется в авторитетных публикациях (это реальная ситуация для всех рассматриваемых здесь компонентов). Значение
] для этой реакции имеется в авторитетных публикациях (это реальная ситуация для всех рассматриваемых здесь компонентов). Значение
![]() при некоторой другой температуре t для того же самого j-го компонента тогда выражается формулой
при некоторой другой температуре t для того же самого j-го компонента тогда выражается формулой
|
|
(E.2) |
или, что то же:
|
|
(E.3) |
где
t0 = 25°С;
![]() - молярная энтальпия идеального газа;
- молярная энтальпия идеального газа;
![]() - изобарическая молярная теплоемкость k-го компонента (исключая образовавшуюся воду, которая рассматривается как жидкость). Суммирование проводится по всем компонентам k, которые появляются в реакции сгорания (максимум 6 в самом общем случае);
- изобарическая молярная теплоемкость k-го компонента (исключая образовавшуюся воду, которая рассматривается как жидкость). Суммирование проводится по всем компонентам k, которые появляются в реакции сгорания (максимум 6 в самом общем случае);
vk - стехиометрический коэффициент для k-го компонента, рассматриваемый как положительный для реагентов (единица для «целевого» j-го компонента) и отрицательный для продуктов сгорания.
Таким образом, вычисление сводится к получению информации h° или ![]() как функциях температуры для
«целевого» j-го компонента и пяти «дополнительных» компонентов O2, СO2, N2 и SO2 (в газовой фазе) и жидкой
воды. Величины h° и
как функциях температуры для
«целевого» j-го компонента и пяти «дополнительных» компонентов O2, СO2, N2 и SO2 (в газовой фазе) и жидкой
воды. Величины h° и ![]() являются сложными функциями температуры, чаще всего выражаемыми в виде полинома
для всех компонентов.
являются сложными функциями температуры, чаще всего выражаемыми в виде полинома
для всех компонентов.
Для описания изменений h° и ![]() в зависимости от температуры в течение многих лет использовалось несколько типов полиномиальных выражений. Для рассматриваемых здесь задач диапазон изменения температуры
мал (максимум 25 К). В частности, как следствие этого, весь второй член в правой части формул (Е.2) и (Е.3) мал по
сравнению с первым членом и, независимо от типа интерполяции, должны получаться существенно идентичные
результаты для
в зависимости от температуры в течение многих лет использовалось несколько типов полиномиальных выражений. Для рассматриваемых здесь задач диапазон изменения температуры
мал (максимум 25 К). В частности, как следствие этого, весь второй член в правой части формул (Е.2) и (Е.3) мал по
сравнению с первым членом и, независимо от типа интерполяции, должны получаться существенно идентичные
результаты для ![]() . Соответствующие данные для вычисления
. Соответствующие данные для вычисления ![]() при конкретных значениях температуры
можно найти для нескольких компонентов природного газа (не обращаясь к полиномиальным выражениям) в работах Армстронга и Джоба [8]
и Гарвина и др. [9],
[10].
Соответствующие полиномиальные выражения, приведенные в
работе Пассута и Даннера [6],
или в модифицированном виде Уилхойта-Харменса [11]-[13],
также могут оказаться полезными. Там, где это возможно, вычисления
при конкретных значениях температуры
можно найти для нескольких компонентов природного газа (не обращаясь к полиномиальным выражениям) в работах Армстронга и Джоба [8]
и Гарвина и др. [9],
[10].
Соответствующие полиномиальные выражения, приведенные в
работе Пассута и Даннера [6],
или в модифицированном виде Уилхойта-Харменса [11]-[13],
также могут оказаться полезными. Там, где это возможно, вычисления ![]() выполнялись разными способами для того, чтобы подтвердить их эквивалентность. Не было обнаружено значительных расхождений (т.е. различия, как правило, были во
втором десятичном знаке, который обычно незначим для точности измерений, и он представлен в таблице 3 только для интерполяции).
выполнялись разными способами для того, чтобы подтвердить их эквивалентность. Не было обнаружено значительных расхождений (т.е. различия, как правило, были во
втором десятичном знаке, который обычно незначим для точности измерений, и он представлен в таблице 3 только для интерполяции).
С целью вывода окончательных значений ![]() (20°С),
(20°С), ![]() (15°С) и
(15°С) и ![]() (0°C) из
(0°C) из ![]() (25°C) для включения их в таблицу 3 в принятых методах вычисления использовали данные работ Гарвина и др. [9],
[10],
Армстронга и Джоба [8]
или модифицированный полином Уилхойта-Харменса [13]
в таком порядке предпочтения. Дополнительные детали
этих вычислений приведены в [3].
(25°C) для включения их в таблицу 3 в принятых методах вычисления использовали данные работ Гарвина и др. [9],
[10],
Армстронга и Джоба [8]
или модифицированный полином Уилхойта-Харменса [13]
в таком порядке предпочтения. Дополнительные детали
этих вычислений приведены в [3].
Е.2 Поправки на неидеальность: объемные эффекты
Объем Vm (идеальный), занимаемый при стандартных условиях измерений (t2, p2) одним молем газа, который ведет себя в соответствии с так называемым законом идеального газа (2.7), определяют по формуле
|
|
(Е.4) |
где
T2 - абсолютная температура, К, которая соответствует температуре t2, °C.
Для реальных газов, к которым относится и природный газ, объем Vm (реальный), занимаемый одним молем реального газа, связан с Vm (идеальный) с помощью коэффициента сжимаемости Z, так что:
|
|
(E.5) |
|
|
(E.6) |
Значение коэффициента сжимаемости, в общем случае, зависит от температуры, давления и состава газа; он может быть больше или (чаще) меньше единицы, но обычно близок к единице для «постоянных» газообразных веществ.
Статистическая физика обеспечивает как понимание общей зависимости Z от температуры, давления и состава, так и способ вычисления его для смеси произвольного состава, исходя из известных свойств компонентов смеси.
Согласно теории основное выражение для Z
|
|
(E.7) |
может быть представлено в виде ряда
|
|
(E.8) |
где Vm (реальный) для краткости сокращен до Vm. В этом выражении В(Т), С(Т),…, Q(T) представляют собой второй, третий,...., q-й вириальные коэффициенты, соответственно. Каждый из них является функцией температуры и состава, но не зависит от давления. Член, содержащий второй вириальный коэффициент, учитывает влияние на Z молекулярных взаимодействий двух частиц (как одинаковых молекул, так и разных); аналогичным образом член, содержащий третий вириальный коэффициент, учитывает влияние взаимодействия трех частиц и так далее. При интересующих нас в настоящем стандарте давлениях взаимодействия трех и более частиц не являются важными, поэтому вириальное разложение можно сократить до второго члена без потери точности.
Таким образом,
Уравнение (E.10) можно решить как квадратичное относительно Zmix, если известен вириальный коэффициент смеси Вmix(Т). Предыдущий текст этого подраздела одинаково применим к чистым газам и смесям.
Статистическая физика также дает следующее выражение для Bmix многокомпонентной смеси произвольного состава
|
|
(E.11) |
где суммирование проводят по всем N компонентам смеси.
В этом выражении есть N членов вида ![]() взаимодействий одинаковых молекул (чистый компонент) и N·(N - 1 )/2 членов вида
взаимодействий одинаковых молекул (чистый компонент) и N·(N - 1 )/2 членов вида ![]() , взаимодействий разных молекул (поскольку нижние индексы теоретически обратимы).
, взаимодействий разных молекул (поскольку нижние индексы теоретически обратимы).
Не имеет смысла в настоящем стандарте приводить числовые значения для всех Bjj (или, что равносильно Zj) и для всех Bjk для каждой температуры, при которой проводятся измерения; это могло бы потребовать около 4620 значений, довольно высокая доля которых могла бы быть основана на некоторой оценочной или корреляционной методике.
Примечание 21 -
Вычисляется как ![]() при N = 55, здесь обычно используют три
значения для Т2.
при N = 55, здесь обычно используют три
значения для Т2.
Ясно, что необходимо существенное уменьшение требований к данным в соответствии с точно понятым (и удобным для анализа) конкретным приближением, если Zmix и, следовательно, Vm (реальный) должны легко вычисляться по формулам (E.10) и (Е.6). Это особенно важно в случае, если метод следует модифицировать для ручного вычисления.
Одна такая конкретная схема приближения, рекомендуемая авторами [7], состоит в сохранении только N членов взаимодействия одинаковых молекул и (N-1) членов взаимодействия разных молекул, включая метан как один из компонентов (т.е. членов вида 2х1·хk·B1k, где нижний индекс 1 относится к метану). Ценность этого приближения состоит в резком уменьшении числа подлежащих оценке членов, а также вириальных коэффициентов в тех членах, сохранение которых обычно допустимо; более того, исключенные члены (т.е. все другие члены 2хj,·хk·Bjk для j, k ¹ 1) можно рассматривать пренебрежимо малыми во многих вычислениях, поскольку xj, xk << x1 для всех j, k.
Однако в настоящем стандарте предпочтение было отдано другой схеме упрощения, которая имеет преимущество в сохранении всех членов, члены взаимодействия одинаковых молекул представляются корректно, а члены взаимодействия разных молекул представляются в соответствии с обсуждаемым приближением. Введенное упрощение можно понять, объединяя формулы (E.9) и (E.11) (записывая В(Т) как В), следующим образом:
|
|
(E.12) |
|
|
(E.13) |
затем (для всех j, k)
в качестве ![]() использовано приближенное выражение - среднее геометрическое величин
использовано приближенное выражение - среднее геометрическое величин ![]() , относящихся к одинаковым молекулам
, относящихся к одинаковым молекулам
|
|
(E.14) |
Хотя в рамках статистической физики нет ее формального обоснования, оно обычно используется для смесей, состоящих из молекул, которые не слишком отличаются по размерам, форме и полярности. Тогда формула (E.13) принимает вид:
|
|
(E.15) |
|
|
(E.16) |
|
|
где bj = 1 - Zj.
В этом выражении сохранены, таким образом, все члены исходной формулы для Zmix, однако, использованы только значения коэффициентов сжимаемости чистых компонентов Zj. Формула (Е.17) создает основу для введения поправок на объем, обусловленный неидеальностью газа, что удобно как для ручных вычислений, так и для получения результата с достаточной точностью.
Однако формулу (Е.17) нельзя использовать некритически. Известно, что существуют ограничения для смесей, содержащих один из трех компонентов, а именно, водород, гелий и диоксид углерода [14].
В первых двух случаях это возникает из-за того, что Zj > 1 при стандартных условиях измерений, так что ![]() является комплексным
числом (то же и в случае неона). Чтобы преодолеть это, водороду, гелию, диоксиду углерода и неону приписаны
«псевдо» значения
является комплексным
числом (то же и в случае неона). Чтобы преодолеть это, водороду, гелию, диоксиду углерода и неону приписаны
«псевдо» значения ![]() и, таким образом, формально формула (Е.17) остается неизменной. Для диоксида углерода
нет необходимости делать такие оговорки, если его молярная доля не превышает 0,15 (см. раздел 1).
и, таким образом, формально формула (Е.17) остается неизменной. Для диоксида углерода
нет необходимости делать такие оговорки, если его молярная доля не превышает 0,15 (см. раздел 1).
Примечание 22 - В [14] была создана основа большинства последующих стандартов в рассматриваемой области; используется индивидуальное рассмотрение при любом содержании водорода. В частности, водород удаляется из суммы, и добавляется к общему выражению дополнительный член. Однако можно показать, что этого можно не делать при условии, что молярная доля водорода в газе не превышает 0,05.
Значения всех Zj и ![]() при трех стандартных значениях температуры измерений приведены в таблице 2 (раздел 10). Использована следующая иерархия способов получения этих значений:
при трех стандартных значениях температуры измерений приведены в таблице 2 (раздел 10). Использована следующая иерархия способов получения этих значений:
a) для постоянных газов наиболее предпочтительно применять коэффициенты сжимаемости, полученные непосредственно из эксперимента или, по крайней мере, оценки коэффициентов сжимаемости, используя хорошее интерполяционное уравнение состояния и высокоточные данные зависимостей от давления, объема и температуры. Значения, приведенные в таблице 2 для таких газов, обычно брались из вторичных публикаций (указанных в [3]), которые удовлетворяют этому критерию;
b) для компонентов, которые не являются газами при стандартных условиях измерений, требуется иной подход. В этом случае обычно принято оценивать значения В(Т) с помощью корреляции Питцера-Керла [15] и пересчитывать это значение в «гипотетическое» значение Z(T, р) с помощью аналога уравнения (E.10) для чистого газа. Корреляционную формулу Питцера-Керла можно записать следующим образом
|
|
(E.18) |
В этой формуле нижний индекс с указывает на значение параметра в критической точке газ-жидкость, нижний индекс r указывает на значение параметра, деленное на значение этого параметра в критической точке (т.е. безразмерное «уменьшенное» значение), а ω - это так называемый коэффициент ацентричности. Значения, используемые для Tс, рс и ω, приведены в разделе В.2 (приложение В). При пересчете значений В в значения Z второй член в правой части уравнения (E.10) был аппроксимирован как р·B(T)/(R·T);
c) имеется несколько компонентов, которые выходят за область применимости методов, приведенных в перечислении а) или b). В частности, исходная корреляция Питцера-Керла была разработана для применения, в основном, к углеводородам и простым неполярным соединениям. Поэтому она не должна применяться к таким компонентам, как вода, метанол, карбонилсульфид и др. Разнообразие методов, которые здесь подробно не рассматриваются (но которые обсуждаются в [3]), были использованы для оценки гипотетических коэффициентов сжимаемости для таких компонентов. На практике ни один из рассмотренных компонентов не будет присутствовать в природном газе или имитаторе природного газа в значительных количествах, так что любая погрешность определения Z не будет существенно влиять на Zmix;
d) наконец, в таблице 2 приведены значения коэффициентов сжимаемости и ![]() для многих веществ, которые являются истинными значениями, за исключением значений
для многих веществ, которые являются истинными значениями, за исключением значений ![]() для водорода, гелия и неона, уже упоминавшихся в примечании 22, которые являются псевдозначениями.
для водорода, гелия и неона, уже упоминавшихся в примечании 22, которые являются псевдозначениями.
Примечание 23 - В настоящее время в США, как это подтверждено на примере стандарта [16],
коэффициент суммирования ![]() четко определен как
четко определен как ![]() . Исходное определение
. Исходное определение ![]() как
как ![]() является предпочтительным и сохраняется в настоящем стандарте.
является предпочтительным и сохраняется в настоящем стандарте.
Е.3 Поправки на неидеальность: эффекты энтальпии
Значение высшей теплоты сгорания идеального газа ![]() для CaHbOcNdSe, рассчитанное на основе значений
молярной доли компонентов, определяемое в разделе 2 как отрицательное значение стандартной энтальпии сгорания обобщенной реакции сгорания [уравнение (Е.1)], в частности, относится к идеальной реакции; т.е. не только к
горючему компоненту, присутствие которого предполагается в состоянии идеального газа, но, следовательно, также и к реагирующему кислороду и всем продуктам (за исключением жидкой воды). Поэтому поправка к энтальпии
сгорания, в принципе, необходима, принимая во внимание тот факт, что реакции сгорания в действительности не
могут происходить таким образом, чтобы все компоненты находились в состоянии идеального газа. Для смеси, какой является природной газ, весь процесс сгорания описывается набором уравнений типа (Е.1) для положительных
чисел a, b, с, d, е.
для CaHbOcNdSe, рассчитанное на основе значений
молярной доли компонентов, определяемое в разделе 2 как отрицательное значение стандартной энтальпии сгорания обобщенной реакции сгорания [уравнение (Е.1)], в частности, относится к идеальной реакции; т.е. не только к
горючему компоненту, присутствие которого предполагается в состоянии идеального газа, но, следовательно, также и к реагирующему кислороду и всем продуктам (за исключением жидкой воды). Поэтому поправка к энтальпии
сгорания, в принципе, необходима, принимая во внимание тот факт, что реакции сгорания в действительности не
могут происходить таким образом, чтобы все компоненты находились в состоянии идеального газа. Для смеси, какой является природной газ, весь процесс сгорания описывается набором уравнений типа (Е.1) для положительных
чисел a, b, с, d, е.
Для такой смеси природного газа, для (первоначально отделенного) кислорода и гомогенного продукта реакции, разница между действительным значением энтальпии одного моля [h(T, p) - h°(T)] и значением h°(t) для идеального газа при той же температуре может быть вычислена с помощью соответствующего уравнения состояния. Для бинарного молекулярного взаимодействия (низкое давление) можно показать [8], что в каждом случае разница в энтальпии может быть представлена формулой
|
|
(E.19) |
где
В(Т, х) - второй вириальный коэффициент для смеси х;
Vm(T, p, x) - объем моля газа, получаемый как положительный результат решения уравнения
|
|
(E.20) |
После этого общая энтальпийная поправка может быть получена как сумма членов с соответствующими весами (т.е. в соответствии со стехиометрией) трех таких членов; вклады от компонентов топлива следует применять с противоположным знаком относительно вкладов от продуктов сгорания.
Вычисления такого рода невозможно выполнить без соответствующего программного обеспечения. Даже при имеющихся компьютерных возможностях это не тривиальная задача, в основном, из-за требований к данным для общей оценки коэффициента В и его температурной производной. К счастью, с помощью модельного вычисления можно показать [8], что для смесей типа природного газа в представляющих интерес условиях общая поправка пренебрежимо мала, обычно она составляет не более 50 Дж·моль-1 (примерно 0,005 %). Влияние энтальпийной поправки в настоящем стандарте далее не рассматривается.
Приложение F
(справочное)
Влияния паров воды на значение теплоты сгорания
F.1 Общая часть
В некоторых калориметрах, используемых для прямого метода измерений объемной теплоты сгорания, перед сжиганием насыщают (во время измерений) горючий газ парами воды, и поэтому будут измерены и, вероятно (но не обязательно) представлены значения теплоты сгорания на (предполагаемой) насыщенной основе. Такие значения будут ниже значений ненасыщенного (сухого или частично насыщенного) газа из-за замещения горючего газа парами воды в измеряемой системе.
Работа других приборов, используемых для прямого или для косвенного определения значения теплоты сгорания, базируется на других принципах.
Например,
- в некоторых калориметрах сгорания газ непосредственно сжигают без предварительной обработки (т.е. с существующим в нем содержанием воды), и результат представляют как истинное значение теплоты сгорания, но приписывают это значение как полученное для сухого газа;
- в некоторых приборах газ высушивают перед определением значения теплоты сгорания; и, таким образом, измеряют и представляют значение для сухого газа, даже если первоначально газ содержал пары воды;
- в приборах, применяемых для определения компонентного состава газов (в частности, газовых хроматографах) обычно анализируются все важные компоненты, за исключением воды, и поэтому вычисленное значение теплоты сгорания относится к осушенному газу, даже если газ в действительности может содержать пары воды.
Поэтому для того, чтобы сделать правильные сравнения значений теплоты сгорания газов, определенных разными методами, необходимо учитывать:
- степень насыщения газа водяным паром в исходном состоянии;
- степень насыщения газа водяным паром в течение процедуры измерения (т.е. после измерения);
- характеристики средства измерений или методики выполнения измерений;
- степень насыщения газа водяным паром, относящуюся к представленному значению теплоты сгорания.
Если все эти факторы известны, можно рассматривать все значения теплоты сгорания, приводя их к одинаковой и согласованной основе.
Хотя основной текст настоящего стандарта относится к вычислениям для осушенного газа, предполагается, что самое логичное основание, в целом, является «общепринятым» основанием, при котором значение теплоты сгорания определяется и регистрируется с любым содержанием паров воды, рассматриваемым просто как один из компонентов смеси с определенной молярной долей. Существует три соображения (F.2-F.4), которые следует учитывать при проведении вычислений, если принят этот подход, особенно, если анализ паров воды не является частью первичной аналитической процедуры (т.е. если о его количестве делают вывод на основе вторичных средств, таких как гигрометрические измерения или измерения точки росы).
F.2 Влияние исключенного объема
Парциальное давление воды pw в природном газе может достигать давления насыщения ps при стандартных условиях измерения состава газа. Традиционным способом оценки влияния паров воды является исключение ее доли pw/ps из объема действительно сухого горючего газа, тем самым, уменьшая определенное значение теплоты сгорания на эту долю до значения
|
|
(F.1) |
где ![]() - значение (высшее или низшее) объемной теплоты сгорания.
- значение (высшее или низшее) объемной теплоты сгорания.
Полностью эквивалентный способ контроля этого влияния (скорее с целью вычисления, а не с целью измерения), но более предпочтительный, поскольку очевидно, что Н может быть представлена в виде значений молярной, массовой или объемной теплоты сгорания, это перейти к оценке компонентного состава в единицах молярной доли. Допустим, что результат анализа компонентного состава газа, выраженный в единицах молярной доли, исключающий пары воды, известен (поскольку такое допущение сделано в основном тексте настоящего стандарта). Если парциальное давление паров воды в пробе теперь как-то определено, то их молярная доля может приниматься за pw/p2. Для того, чтобы сохранить сумму молярных долей всей смеси, равной единице, молярная доля каждого компонента должна быть нормализована умножением на коэффициент (р2 - pw)/p2. Таким образом, поскольку вычисленное значение теплоты сгорания является суммой членов, пропорциональных молярным долям компонентов, то вычисленное значение теплоты сгорания просто сокращается на эту долю (кроме вторичных эффектов, рассмотренных в разделах F.3 и F.4), как это видно из предыдущих рассуждений.
Как видно из следующего примера, это первичное влияние может быть важным. Допустим, мы хотим вычислить значение теплоты сгорания на основе насыщенного газа, исходя из анализа осушенного газа, вероятно, для того, чтобы сделать осмысленное сравнение между аналитически полученным значением теплоты сгорания и значением, определенным с помощью калориметра, в котором тот же газ насыщается во время измерения. Также допустим, что значение объемной теплоты сгорания осушенного газа равно 38,00 МДж·м-3 при стандартных условиях сгорания и измерений: 15°С, 101,325 кПа. При 15°С давление насыщенного пара воды равно 1,705 кПа, и тогда молярная доля воды в природном газе, насыщенном водой при стандартных условиях, равна
|
|
(F.2) |
Таким образом, значение теплоты сгорания насыщенного газа (пренебрегая вторичными эффектами, обсуждаемыми в разделах F.3 и F.4) меньше, чем значение теплоты сгорания сухого газа на (1 - 0,01683), т.е.
|
|
(F.3) |
При разнице в значениях теплоты сгорания вплоть до 1,68 %, в зависимости от количества присутствующего водяного пара, обычно очень важно рассматривать способ, с помощью которого пары воды учитывались путем прямого измерения или анализа компонентов. Особенно сложная ситуация может возникнуть для газа, содержащего пары воды в качестве известного компонента при давлении ниже давления насыщенного пара. В этом случае все «общепринятые» значения теплоты сгорания сухого газа и насыщенного газа могут быть рассчитаны, являются разными и могут быть перепутаны друг с другом.
Примечание - Влагосодержание природного газа, подаваемого в магистральные газопроводы, транспортируемого по ним и поставляемого потребителю, ограничивается требованиями соответствующих нормативных документов, действующих в стране, или условиями контракта.
F.3 Влияние скрытой теплоты (энтальпийный эффект)
Вторичное влияние присутствия паров воды в пробе газа в разделе F.2 не рассматривается. Скрытая теплота испарения воды, образующейся при сгорании углеводородов, является значимым фактором при определении значения теплоты сгорания этих углеводородов и, следовательно, состояние воды точно соответствует определениям, приведенным в 2.1 и 2.2.
В случае высшей теплоты сгорания (2.1) необходимо, чтобы вся вода, образовавшаяся в реакции сгорания, конденсировалась в жидкое состояние при стандартной температуре сгорания t1. Это требование может быть не реализуемым на практике, но оно действительно обеспечивает теоретическую основу вычисления значения высшей теплоты сгорания сухого природного газа. Однако присутствие паров воды в объеме газа до сгорания представляет проблему, как рассматривать состояние воды после сгорания:
a) можно предположить, хотя это не реализуется на практике, что эта вода после сгорания остается в газообразном состоянии, и, таким образом, не оказывает влияния на теплоту сгорания; или
b) можно предположить, что эта вода конденсируется в жидкость при стандартной температуре сгорания t1 и, тем самым повышает теплоту сгорания за счет выделившейся скрытой теплоты испарения воды.
Предполагается, что самая логически непротиворечивая трактовка значения высшей теплоты сгорания состоит в допущении того, что вся вода, как находящаяся в объеме газа до сгорания, так и образующаяся при сгорании, конденсируется в жидкость при стандартной температуре сгорания t1 Поэтому пары воды, содержащиеся в объеме газа, должны рассматриваться как компонент природного газа с конкретным значением молярной доли и имеющий значение теплоты сгорания, полученное из скрытой теплоты испарения воды; другими словами, в суммировании есть другой член хj·Нj для воды. Вот почему значения высшей теплоты сгорания для паров воды, приведенные в таблицах 3-5, не равны нулю. Такая трактовка приводит только к небольшому повышению значения теплоты сгорания; при допущении о насыщении парами воды это повышение не зависит от состава газа и зависит только от измеренной температуры газа. Повышение теплоты сгорания, рассчитанное на основе значений объемной доли компонентов, для насыщенного газа составит:
для измерений при 0°С - 0,01 МДж·м-3;
для измерений при 15°С - 0,03 МДж·м-3;
для измерений при 20°С - 0,045 МДж·м-3.
Для значения низшей теплоты сгорания весь водяной пар остается в газовой фазе и поэтому энтальпийный эффект такого рода не рассматривается.
F.4 Влияние коэффициента сжимаемости
Существует третий эффект, влияние которого еще меньше, но, тем не менее, он должен учитываться. Присутствие паров воды влияет на коэффициент сжимаемости смеси и, таким образом, изменяет значение объемной теплоты сгорания реального газа. При 15°С для типичного природного газа значение Z при переходе от осушенного к насыщенному состоянию меняется только на 0,0004 (от 0,9981 до 0,9977).
Основной текст настоящего стандарта относится только к сухому природному газу, поскольку такое состояние рекомендуется как предпочтительное. В случае необходимости выполнения вычислений для природного газа, содержащего пары воды, следует, однако, учитывать упомянутые выше эффекты при принятии решения о соответствующем подходе.
F.5 Пересчет различных единиц влагосодержания природного газа
В тех случаях, когда содержание водяного пара в природном газе известно в единицах температуры точки росы влаги или в единицах массовой концентрации, проводят пересчет этих значений в значение влагосодержания, выраженное в единицах молярной доли.
Значение молярной доли водяного пара (![]() , %) устанавливают путем пересчета значения температуры точки росы влаги, измеренной при конкретных условиях, сначала в значение массовой концентрации водяного пара в граммах на кубический дециметр при давлении 101,325 кПа и температуре 0 или 20°С и затем в
значение молярной доли водяного пара
, %) устанавливают путем пересчета значения температуры точки росы влаги, измеренной при конкретных условиях, сначала в значение массовой концентрации водяного пара в граммах на кубический дециметр при давлении 101,325 кПа и температуре 0 или 20°С и затем в
значение молярной доли водяного пара ![]() в процентах.
в процентах.
Для пересчета значения температуры точки росы влаги природного газа, измеренного при конкретных
условиях, в значение массовой концентрации водяного пара ![]() , выраженной в граммах на кубический
дециметр, используют данные ГОСТ 20060 [17].
, выраженной в граммах на кубический
дециметр, используют данные ГОСТ 20060 [17].
Пересчет значения массовой концентрации водяного пара (![]() , г/м3) в значение молярной доли (
, г/м3) в значение молярной доли (![]() , %), проводят в соответствии с формулами:
, %), проводят в соответствии с формулами:
для стандартных условий 20°С и 101,325 кПа
|
|
(F.4) |
и для стандартных условий 0°С и 101,325 кПа
|
|
(F.5) |
Приложение G
(справочное)
Обобщение, обсуждение и выбор значения теплоты сгорания метана
Энтальпия сгорания метана безусловно является самым важным значением физического свойства, используемого при определении значения теплоты сгорания природного газа. Метан не только является основным компонентом природного газа, но метан особой чистоты часто используют в качестве градуировочного газа для калориметров непрерывного принципа действия, обычно применяемых для измерений значения теплоты сгорания природного газа.
Теплота сгорания метана была впервые определена в 1848 г., и с тех пор было опубликовано 8 исследований. Однако, в научной литературе имеется только два набора значений стандартной молярной энтальпии сгорания при 25°С для метана нормального изотопного состава, измеренные с уровнем точности и прецизионности, соответствующим возможностям современной измерительной техники, которые можно было бы применить для настоящего стандарта.
Это - исследования Россини (1931) [18] и Питтама и Пилчера (1972) [19].
Значения, полученные при этих двух исследованиях, приведены ниже (значения Россини были пересмотрены в работе Армстронга и Джоба [8] в соответствии с установленной на сегодняшний день молярной массой, температурной шкалой и др.).
|
Россини [18], кДж·моль-1: |
Питтам и Пилчер [19], кДж·моль-1: |
|
-891,823 |
-890,36 |
|
-890,633 |
-891,23 |
|
-890,013 |
-890,62 |
|
-890,503 |
-890,24 |
|
-890,340 |
-890,61 |
|
-890,061 |
-891,17 |
При анализе своих собственных данных Россини [18] отбросил самое высокое (первое) значение как выброс и на основании оставшихся пяти точек получил среднее значение (-890,31 ±0,27) кДж·моль-1. Питам и Пилчер [19] использовали все шесть точек данных для вычисления среднего значения (-890,71 ±0,41) кДж·моль-1. (Неопределенность приведенных значений представляет одно стандартное отклонение).
При пересмотре этих двух исследований Армстронг и Джоб [8] сделали вывод, что хотя они и согласились с обработкой Россини [18] его собственных данных, приведших к отбрасыванию одной точки как выброса, но если взять вместе все точки данных как единый ряд, то после этого нет явного статистического доказательства того, что следует отказаться от любой другой точки. Армстронг и Джоб [8] также рассмотрели некоторые технические и расчетные аспекты, которые остаются правильными; они, наряду с некоторыми дополнительными аспектами, таковы:
a) уровни примеси в пробе метана: использовавшийся Россини [18] метан содержал 1210 ppm оксида углерода, на которую была внесена поправка, тогда как Питтам и Пилчер [19] использовали пробу, содержащую менее 5 ppm примесей;
b) определение полноты реакции: Россини [18] измерял количество образовавшейся воды стандартным методом, в то время как Питтам и Пилчер измеряли количество образовавшегося диоксида углерода, что в настоящее время считается предпочтительным;
c) методы калибровки и прослеживаемости: Россини [18] калибровал свой калориметр с помощью метода электронагрева с прослеживаемостью к эталонам Национального бюро стандартов, тогда как Питтам и Пилчер [19] для калибровки использовали сгорание водорода с прослеживаемостью к более ранней работе Россини по сгоранию водорода;
d) корреляция значений теплоты образования серии алканов: анализ нескольких значений теплоты образования (полученных из значений теплоты сгорания) гомологической серии н-алканов более низкой молекулярной массы благоприятствует получению более однородных значений в отношении прироста групп СН2, полученных Питтамом и Пилчером, и можно предположить, что это значение для метана находится между значениями, полученными при этих двух исследованиях;
e) «изолирование» калориметров: Россини [18] использовал масляные пленки для «изоляции» калориметра в каждом отдельном эксперименте (повторную сборку калориметра каждый раз), а Питтам и Пилчер [19] заявляли, что калориметр был «изолирован» в течение серии испытаний, но на самом деле после каждого эксперимента удаляли платиновый термометр сопротивления и заменяли его ртутным терморегулятором, что приводило к возможной потере воды;
f) повторная сборка калориметра: Россини [18] заново собирал калориметр перед каждым экспериментом, заполняя его взвешенным количеством воды и относя его калибровку и сгорание к стандартной массе воды, тогда как Питтам и Пилчер [19] калибровали свой калориметр во время серии экспериментов, а затем использовали этот энергетический эквивалент в течение всей работы, даже после разборки, внесения изменений и повторной сборки калориметра, обоснованием для использования одного и того же энергетического эквивалента, вероятно, является, одинаковая масса воды, используемая для повторного заполнения калориметра.
В конечном счете трудно или даже невозможно проанализировать эти различные аспекты и количественно оценить их влияние на совокупности данных для того, чтобы решить, какой из двух наборов данных следует использовать или, если следует использовать оба набора, то с какими весовыми коэффициентами для отдельных данных.
Поэтому в настоящем стандарте было решено каждому набору данных приписать равную весовую значимость, что приводит к стандартной энтальпии сгорания метана при 25°С, равной (-890,63 ±0,53) кДж·моль-1 с только одной экспериментальной точкой, вышедшей за пределы двух стандартных отклонений от среднего значения. Эта точка зрения находится в соответствии с выводом, полученным в окончательном отчете Гарвина [20] по проекту, для которого более ранний отчет Армстронга и Джоба [8] был промежуточной публикацией.
Примечание 24 - Четвертая точка в данных Питтама и Пилчера [19], к сожалению, неправильно напечатана как «-890,34» в [8]: следовательно, общее среднее значение, приведенное в работах [8] и [3], имеет погрешность 0,02 кДж·моль-1.
Для удобства непротиворечивый набор результатов значений теплоты сгорания для метана для всех условий, рассмотренных в настоящем стандарте, приведен в таблицах G.1-G.3.
Таблица G.1 - Значение удельной молярной теплоты сгорания метана (неопределенность ±1,0 кДж·моль-1 при доверительной вероятности 95 %)
|
Теплота сгорания |
°С |
кДж·моль-1 |
|
Высшая |
25 |
890,63 |
|
Высшая |
20 |
891,09 |
|
Высшая |
15 |
891,56 |
|
Высшая |
0 |
892,97 |
|
Низшая |
25 |
802,60 |
|
Низшая |
20 |
802,65 |
|
Низшая |
15 |
802,69 |
|
Низшая |
0 |
802,82 |
Таблица G.2 - Значение удельной массовой теплоты сгорания метана (неопределенность ±0,06 МДж·кг-1 при доверительной вероятности 95 %)
|
Теплота сгорания |
°С |
МДж·кг-1 |
|
Высшая |
25 |
55,516 |
|
Высшая |
20 |
55,545 |
|
Высшая |
15 |
55,574 |
|
Высшая |
0 |
55,662 |
|
Низшая |
25 |
50,029 |
|
Низшая |
20 |
50,032 |
|
Низшая |
15 |
50,035 |
|
Низшая |
0 |
50,043 |
Таблица G.3 - Значение удельной объемной теплоты сгорания метана (неопределенность ±0,05 МДж·м-3 при доверительной вероятности 95 %)
|
Описание |
МДж м-3 |
|
Идеальный газ, высшая, сгорание при 25°С, измерение при 0°С |
39,735 |
|
Идеальный газ, высшая, сгорание при 15°С, измерение при 0°С |
39,777 |
|
Идеальный газ, высшая, сгорание при 15°С, измерение при 15°С |
37,706 |
|
Идеальный газ, высшая, сгорание при 0°С, измерение при 0°С |
39,840 |
|
Идеальный газ, высшая , сгорание при 20°С, измерение при 20°С |
37,044 |
|
Идеальный газ, высшая, сгорание при 25 °С, измерение при 20 °С |
37,024 |
|
Идеальный газ, низшая, сгорание при 25°С, измерение при 0°С |
35,808 |
|
Идеальный газ, низшая, сгорание при 15°С, измерение при 0°С |
35,812 |
|
Идеальный газ, низшая, сгорание при 15°С, измерение при 15°С |
33,948 |
|
Идеальный газ, низшая, сгорание при 0°С, измерение при 0°С |
35,818 |
|
Идеальный газ, низшая, сгорание при 20°С, измерение при 20°С |
33,367 |
|
Идеальный газ, низшая, сгорание при 25°С, измерение при 20°С |
33,365 |
|
Реальный газ, высшая, сгорание при 25°С, измерение при 0°С |
39,831 |
|
Реальный газ, высшая, сгорание при 15°С, измерение при 0°С |
39,872 |
|
Реальный газ, высшая, сгорание при 15°С, измерение при 15°С |
37,782 |
|
Реальный газ, высшая, сгорание при 0°С, измерение при 0°С |
39,936 |
|
Реальный газ, высшая, сгорание при 20°С, измерение при 20°С |
37,115 |
|
Реальный газ, высшая, сгорание при 25°С, измерение при 20°С |
37,095 |
|
Реальный газ, низшая, сгорание при 25°С, измерение при 0°С |
35,894 |
|
Реальный газ, низшая, сгорание при 15°С, измерение при 0°С |
35,898 |
|
Реальный газ, низшая, сгорание при 15°С, измерение при 15°С |
34,016 |
|
Реальный газ, низшая, сгорание при 0°С, измерение при 0°С |
35,904 |
|
Реальный газ, низшая, сгорание при 20°С, измерение при 20°С |
33,431 |
|
Реальный газ, низшая, сгорание при 25°С, измерение при 20°С |
33,428 |
Приложение Н
(справочное)
Вывод формул, связанных с прецизионностью
Формулы (6, 11, 15, 17, 18) были выведены следующим образом.
Н.1 Метан по разности
Фундаментальная формула, приведенная в основном тексте настоящего стандарта для вычисления идеального значения теплоты сгорания, исходя из компонентного состава, выраженного в молярных долях, будет иметь вид
|
|
(Н.1) |
В том случае, если анализируются все компоненты, за исключением метана, содержание которого вычисляют по разности, действительно имеются N-1 независимых переменных состава хj, а формулу (Н.1) можно переписать следующим образом
|
|
(Н.2) |
где
![]() - идеальное значение теплоты сгорания смеси;
- идеальное значение теплоты сгорания смеси;
х1 - молярная доля метана, вычисляемая по формуле
![]()
где
xj - молярная доля j-го компонента;
![]() - идеальное значение теплоты сгорания метана;
- идеальное значение теплоты сгорания метана;
![]() - идеальное значение теплоты сгорания j-го компонента.
- идеальное значение теплоты сгорания j-го компонента.
Формула (Н.2) может быть преобразована путем подстановки выражения для переменной следующим образом
|
|
(Н.3) |
|
|
(Н.4) |
Для каждого члена в сумме можно образовать частную производную следующим образом
|
|
(Н.5) |
Поэтому вклад сходимости Dхj от переменной хj в сходимость ![]() будет равен
будет равен
|
|
(Н.6) |
Если все N-1 таких членов объединяются в квадратичной форме, мы получим формулу (18)
|
|
(H.7) |
Н.2 Метан по анализу
Если анализируют все компоненты, включая метан, то получают N независимых переменных компонентов
смеси ![]() , но они не входят в общую сумму до единицы, как это требуется для ввода в формулу (Н.1). В этом случае
формулу можно переписать следующим образом
, но они не входят в общую сумму до единицы, как это требуется для ввода в формулу (Н.1). В этом случае
формулу можно переписать следующим образом
|
|
(H.8) |
где
|
|
(H.9) |
Для каждого члена в формуле (H.8) можно образовать частную производную следующим образом
|
|
(H.10) |
или
|
|
(H.11) |
где
|
|
(H.12) |
Следовательно, игнорируя коэффициент К,
который всегда близок к единице для приемлемых экспериментальных результатов, вклад сходимости ![]() от переменной
от переменной ![]() в сходимость
в сходимость ![]() задается формулой
задается формулой
|
|
(H.13) |
Если все N таких членов суммируются в квадратичной форме, получим формулу (19)
|
|
(H.14) |
Отметим, что сходимости компонентов ![]() являются сходимостями ненормализованных молярных долей
являются сходимостями ненормализованных молярных долей ![]() даже хотя сама
даже хотя сама ![]() вычисляется с помощью нормализованных молярных долей xj.
вычисляется с помощью нормализованных молярных долей xj.
Это выражение можно переписать в измененной форме. Формулу (H.13) можно переписать как
|
|
(H.15) |
Если все N таких членов суммируются в квадратичной форме и перегруппировываются, получаем
|
|
(H.16) |
Отметим, что сходимости компонентов в этом выражении снова те же сходимости ненормализованных молярных долей, хотя сами молярные доли являются нормализованными значениями.
Формулы (22) и (23) были выведены с использованием аргументов, подобных тем, которые привели к формулам (H.7) и (H.14), соответственно.
Формула (24) получена суммированием квадратов относительных сходимостей соответствующих членов в исходном выражении для идеального числа Воббе следующим образом
|
|
(H.17) |
которое математически идентично формуле
|
|
(H.18) |
Приложение J
(справочное)
Приблизительные коэффициенты пересчета теплоты сгорания при переходе от одной стандартной температуры к другой стандартной температуре
Для получения значений физико-химических показателей качества природного газа при стандартных условиях, приведенных в строке b), из известного значения физико-химического показателя в тех же самых единицах измерения при стандартных условиях, приведенных в строке a), его умножают на коэффициент, указанный в таблицах J.1, J.2 или J.3. Для выполнения обратного пересчета делят на указанный коэффициент. Ожидается, что погрешность пересчета свойств идеального газа будет в пределах ±0,01 % для всех встречающихся составов природного газа. Для объемных свойств реальных газов (коэффициента сжимаемости, плотности и относительной плотности) ожидаемая погрешность будет в пределах ±0,02 %, а для свойств сгорания (теплоты сгорания и числа Воббе) будет в пределах ±0,1 %.
Таблица J.1 - Коэффициенты пересчета для значений теплоты сгорания
|
|
Температура сгорания, °С |
||
|
а) |
25 |
25 |
15 |
|
|
в |
в |
в |
|
b) |
15 |
0 |
0 |
|
Высшая удельная молярная теплота сгорания |
1,0010 |
1,0026 |
1,0016 |
|
Низшая удельная молярная теплота сгорания |
1,0001 |
1,0003 |
1,0002 |
|
Высшая удельная массовая теплота сгорания |
1,0010 |
1,0026 |
1,0016 |
|
Низшая удельная массовая теплота сгорания |
1,0001 |
1,0003 |
1,0002 |
Таблица J.2 - Коэффициенты пересчета для значений относительной плотности, плотности и коэффициента сжимаемости
|
|
Температура измерений, °С |
||
|
b) |
20 |
20 |
15 |
|
|
в |
в |
в |
|
а) |
15 |
0 |
0 |
|
Плотность идеальных газов |
1,0174 |
1,0732 |
1,0549 |
|
Относительная плотность идеальных газов |
1,0000 |
1,0000 |
1,0000 |
|
Коэффициент сжимаемости |
0,9999 |
0,9995 |
0,9996 |
|
Плотность реальных газов |
1,0175 |
1,0738 |
1,0553 |
|
Относительная плотность реальных газов |
1,0001 |
1,0003 |
1,0002 |
Таблица J.3 - Коэффициенты пересчета для значений теплоты сгорания и числа Воббе
|
|
Температура сгорания, °С + температура измерений, °С |
|||||||||
|
а) |
25+20 |
25+20 |
25+20 |
25+20 |
25+0 |
25+0 |
25+0 |
15+15 |
15+15 |
15+15 |
|
|
в |
в |
в |
в |
в |
в |
в |
в |
в |
в |
|
b) |
25+0 |
15+15 |
15+0 |
0+0 |
15+15 |
15+0 |
0+0 |
15+0 |
0+0 |
0+0 |
|
Высшая объемная теплота сгорания для идеального газа |
1,0732 |
1,0184 |
1,0743 |
1,0760 |
0,9489 |
1,0010 |
1,0026 |
1,0549 |
1,0566 |
1,0016 |
|
Низшая объемная теплота сгорания для идеального газа |
1,0732 |
1,0175 |
1,0733 |
1,0735 |
0,9481 |
1,0001 |
1,0003 |
1,0549 |
1,0551 |
1,0002 |
|
Число Воббе для идеального газа |
1,0732 |
1,0184 |
1,0743 |
1,0760 |
0,9489 |
1,0010 |
1,0026 |
1,0549 |
1,0566 |
1,0016 |
|
Высшая объемная теплота сгорания для реального газа |
1,0738 |
1,0185 |
1,0749 |
1,0766 |
0,9486 |
1,0010 |
1,0026 |
1,0553 |
1,0570 |
1,0016 |
|
Низшая объемная теплота сгорания для реального газа |
1,0738 |
1,0176 |
1,0739 |
1,0741 |
0,9477 |
1,0001 |
1,0003 |
1,0553 |
1,0555 |
1,0002 |
|
Число Воббе для реального газа |
1,0736 |
1,0185 |
1,0747 |
1,0764 |
0,9487 |
1,0010 |
1,0026 |
1,0552 |
1,0569 |
1,0016 |
Приложение К
(справочное)
Компьютерная реализация рекомендованных методов 1)
Отлаженную компьютерную программу, реализующую предпочтительные методики и рекомендации, описанные в настоящем стандарте, можно получить через организации-члены ИСО или через Центральный секретариат ИСО.
Эта программа поставляется на современных носителях. Технические характеристики, условия поставки и цену за копию рабочей программы можно получить по запросу.
Программа первоначально была написана для применения с IBM-совместимыми персональными компьютерами. Программирование было выполнено IBM-совместимой операционной системой под MS-DOS 3.10, версия 3.13; язык программирования: GW-BASIC 3.21, версия 3.25. Исходная программа combust.ach была конвертирована в рабочую программу с помощью Microsoft Quickbasic компилятора 2.02, версия 1.20.
Как указано выше, combust.exe реализует процедуры и рекомендации настоящего стандарта. Физико-химические показатели природного газа, считываемые с дисплея монитора и/или распечатки, следующие:
значение высшей молярной теплоты сгорания __________, кДж·моль-1;
значение низшей молярной теплоты сгорания __________, кДж·моль-1;
значение высшей массовой теплоты сгорания __________, МДж·кг-1;
значение низшей массовой теплоты сгорания __________, МДж·кг-1;
значение высшей объемной теплоты сгорания __________, МДж·м-3;
значение низшей объемной теплоты сгорания __________, МДж·м-3;
средняя молекулярная масса __________;
коэффициент сжимаемости __________;
относительная плотность (по воздуху) __________;
плотность __________, кг·м-3;
число Воббе __________, МДж·м-3.
Пользователь может выбрать вычисления приведенных выше показателей для идеального либо для реального газа и либо «по анализу» (сухого) или насыщенного водой газа для любого из набора стандартных условий:
измерение при 0°С и сгорание при 25°С;
измерение при 0°С и сгорание при 15°С;
измерение и сгорание при 0°С;
измерение и сгорание при 15°С;
измерение и сгорание при 20°С;
измерение при 20°С и сгорание при 25°С.
Во всех случаях стандартное давление равно 101,325 кПа. Программа позволяет выбрать необходимые соответствующие стандартные условия.
Примечание 25 - Значения объемной теплоты сгорания в британских тепловых единицах на кубический фунт при 60/60°F также можно вычислить из значений в мегаджоулях на кубический метр при 15/15°С для ряда стандартных давлений, но метод, использованный для этих вычислений, не является частью настоящего стандарта.
Примечание 26 - Кроме того, программа вычисляет следующие свойства, но опять-таки использованный метод не рассматривается в настоящем стандарте:
нижний предел воспламеняемости в воздухе при 25°С (в объемных долях) __________, %;
верхний предел воспламеняемости в воздухе при 25°С (в объемных долях) __________, %;
стехиометрическое требование по воздуху __________, по объему.
После загрузки combust.exe вся вводная информация запрашивается удобным для пользователя способом. Кроме выбора опций, все что пользователь должен представить - состав в молярных долях (или процентах) и идентификационный код пробы. Имеется несколько встроенных ловушек ошибок, которые, не разрушая программы, выявляют неправильные вводы, такие как нехватка вводимых молярных долей, чтобы сумма равнялась единице или молярной доли метана ниже нижнего допустимого предела в 0,5. Предусмотрена сигнализация о неправильных вводах для выбора опций.
Одной полезной опцией является возможность прямого вывода на принтер. С бумажной копией (но не с отображением на мониторе) появляется дополнительная опция перечисления состава проб вместе с числовыми результатами. Эта возможность выдвигает на первый план важную техническую проблему, касающуюся вычислений для насыщенных газов. Такие вычисления выполняются в соответствии с принципом, который состоит в том, что если выбирается «насыщенная» опция, то состав пробы газа нормализуется (после проверок правильности) как новый состав, который отражает присутствие паров воды (при соответствующем давлении насыщенных паров) как дополнительного компонента смеси, присутствующего при определенном значении молярной доли. Затем программа вычисляет показатели насыщенной смеси для этого исправленного состава. В результате распечатанный список состава насыщенного газа не является таким же, как начальный «сухой» состав и представленное значение высшей теплоты сгорания учитывает теплоту, выделившуюся при конденсации как паров воды, образовавшихся при сгорании, так и воды, присутствующей в насыщенной смеси (приложение F).
Типичная распечатка приведена ниже. Она представлена для реального, сухого газа состава, использованного для показательных вычислений, приведенных в приложении D при тех же стандартных условиях (15/15°С).
Примечание 27 - Хотя программа combust.exe и связанные с ней файлы species.dat, molwt.dat, zz-00.dat, zz-15.dat, zz-20.dat, cv-00.dat, cv-15.dat, cv-20.dat, cv-25.dat, water.dat, stoic.dat, lower.dat, upper.dat и refcons.txt стали легально доступными, нет гарантии их применения в контрактных или других коммерческих целях и нет гарантии того, что они не содержат ошибок. Однако они долгое время проверялись несколькими экспертами и в настоящее время при передаче на печать не содержат каких-либо ошибок.
Воспроизведение типичной распечатки
|
Пример для смеси/пробы |
14 сентября 1994 г |
|
Состав (моль/моль) |
|
|
Метан |
= 0,92470 |
|
Этан |
= 0,03500 |
|
Пропан |
= 0,00980 |
|
н-Бутан |
= 0,00220 |
|
2-Метилпропан |
= 0,00340 |
|
н-Пентан |
= 0,00060 |
|
Азот |
= 0,01750 |
|
Диоксид углерода |
= 0,00680 |
Сгорание при 15°С, измерение при 15°С и 101,325 кПа.
Для реального сухого газа:
значение высшей молярной теплоты сгорания - 919,09 кДж·моль-1;
значение низшей молярной теплоты сгорания - 829,1 кДж·моль-1;
значение высшей массовой теплоты сгорания - 52,59 МДж·кг-1;
значение низшей массовой теплоты сгорания - 47,44 МДж·кг-1;
значение высшей объемной теплоты сгорания - 38,96 МДж·м-3;
значение низшей объемной теплоты сгорания - 35,15 МДж·м-3;
средняя молярная масса - 17,478;
коэффициент сжимаемости - 0,9977;
относительная плотность - 0,6046;
плотность - 0,7409 кг·м-3;
число Воббе - 50,11 МДж·м-3;
стехиометрическое требование к отношению воздух/газ - 9,85 по объему;
нижний предел воспламеняемости в воздухе при 25°С - 4,8 % (V/V) (газ/смесь);
верхний предел воспламеняемости в воздухе при 25°С - 15,1 % (V/V) (газ/смесь).
1) Описываемое в настоящем приложении программное обеспечение в настоящее время является морально и технически устаревшим. Текст описания программного обеспечения представляет интерес исключительно в аспекте ознакомления с расчетным алгоритмом.
Для выяснения возможности получения программы, реализующей процедуры и рекомендации настоящего стандарта с использованием современных компьютерных/информационных технологий, необходимо подать запрос в организацию - член ИСО или в Центральный секретариат ИСО.
Приложение L
(справочное)
Значения молярной теплоты сгорания для стандартной температуры 60°F
Таблица L.1 - Значения молярной теплоты сгорания природного газа при 60°F для идеального газа
Все значения ![]() (60°F) и
(60°F) и ![]() (60°F) были получены с помощью конкретного вычисления из
(60°F) были получены с помощью конкретного вычисления из ![]() (25°C) (раздел Е.1, приложение
Е).
(25°C) (раздел Е.1, приложение
Е).
|
Компонент |
Значение
молярной теплоты сгорания |
|
|
высшей |
низшей |
|
|
1 Метан |
891,51 |
802,69 |
|
2 Этан |
1562,06 |
1428,83 |
|
3 Пропан |
2220,99 |
2043,35 |
|
4 н-Бутан |
2879,63 |
2657,58 |
|
5 2-Метилпропан |
2870,45 |
2648,40 |
|
6 н-Пентан |
3538,44 |
3271,98 |
|
7 2-Метилбутан |
3531,52 |
3265,06 |
|
8 2,2-Диметилпропан |
3517,27 |
3250,81 |
|
9 н-Гексан |
4198,06 |
3887,19 |
|
10 2-Метилпентан |
4190,43 |
3879,57 |
|
11 3-Метилпентан |
4193,03 |
3882,17 |
|
12 2,2-Диметилбутан |
4180,64 |
3869,78 |
|
13 2,3-Диметилбутан |
4188,41 |
3877,55 |
|
14 н-Гептан |
4856,97 |
4501,69 |
|
15 н-Октан |
5515,77 |
5116,08 |
|
16 н-Нонан |
6175,56 |
5731,46 |
|
17 н-Декан |
6834,61 |
6346,11 |
|
18 Этилен |
1412,06 |
1323,24 |
|
19 Пропилен |
2059,35 |
1926,12 |
|
20 1-Бутен |
2718,59 |
2540,96 |
|
21 цис-2-Бутен |
2711,8 |
2534,2 |
|
22 транс-2-Бутен |
2708,2 |
2530,5 |
|
23 2-Метилпропен |
2701,9 |
2524,3 |
|
24 1-Пентен |
3377,62 |
3155,57 |
|
25 Пропадиен |
1943,91 |
1855,09 |
|
26 1,2-Бутадиен |
2595,05 |
2461,82 |
|
27 1,3-Бутадиен |
2542,03 |
2408,80 |
|
28 Ацетилен |
1301,35 |
1256,94 |
|
29 Циклопентан |
3322,04 |
3100,00 |
|
30 Метилциклопентан |
3972,29 |
3705,83 |
|
31 Этилциклопентан |
4631,75 |
4320,89 |
|
32 Циклогексан |
3955,85 |
3689,39 |
|
33 Метилциклогексан |
4603,90 |
4293,03 |
|
34 Этилциклогексан |
5266,73 |
4911,46 |
|
35 Бензол |
3302,78 |
3169,55 |
|
36 Толуол |
3949,70 |
3772,07 |
|
37 Этилбензол |
4609,40 |
4387,35 |
|
38 о-Ксилол |
4598,51 |
4376,46 |
|
39 Метанол |
765,03 |
676,21 |
|
40 Метантиол |
1240,23 |
1151,41 |
|
41 Водород |
286,13 |
241,72 |
|
42 Вода1) |
44,410 |
0 |
|
43 Сульфид водорода |
562,36 |
517,95 |
|
44 Аммиак |
383,47 |
316,86 |
|
45 Цианид водорода |
671,7 |
649,5 |
|
46 Монооксид углерода |
282,91 |
282,91 |
|
47 Карбонил сульфид |
548,15 |
548,15 |
|
48 Карбонил дисульфид |
1104,33 |
1104,33 |
|
1) Ненулевое значение теплоты сгорания паров воды, полученное формально из определения значения высшей теплоты сгорания, которое требует конденсации в жидкое состояние всех паров воды в продуктах сгорания. Таким образом, все пары воды, присутствующие тем или иным образом в сухом газе, дают свой вклад за счет скрытой теплоты испарения в значение высшей теплоты сгорания смеси (более полное объяснение - приложение F). |
||
Значения ![]() (60°F) - высшей или низшей массовой теплоты сгорания можно вычислить из значения молярной теплоты сгорания
(60°F) - высшей или низшей массовой теплоты сгорания можно вычислить из значения молярной теплоты сгорания ![]() с помощью методов, приведенных в разделе 6.
с помощью методов, приведенных в разделе 6.
Значения ![]() (60°F) - высшей или низшей объемной теплоты сгорания можно вычислить из значения молярной теплоты сгорания
(60°F) - высшей или низшей объемной теплоты сгорания можно вычислить из значения молярной теплоты сгорания ![]() с помощью методов, приведенных в разделе 7.
с помощью методов, приведенных в разделе 7.
Приложение М
(обязательное)
Требования к точности определения компонентного состава природного газа и расширенная неопределенность для значений теплоты сгорания и плотности
Таблица М.1 - Требования к точности определения компонентного состава природного газа
|
Наименование компонента |
Диапазон значений молярной доли, % |
Расширенная абсолютная неопределенность U(x)1), %, при коэффициенте охвата k = 2 |
|
Метан |
40-99,97 |
-0,0187·х + 1,882) -0,0023·х + 0,293) |
|
Этан |
0,001 - 15 |
0,04·х + 0,00026 |
|
Пропан |
0,001 - 6,0 |
0,06·х + 0,00024 |
|
Изобутан |
0,001 - 4,0 |
0,06·х + 0,00024 |
|
н-Бутан |
0,001 - 4,0 |
0,06·х + 0,00024 |
|
Изопентан |
0,001 - 2,0 |
0,06·х + 0,00024 |
|
н-Пентан |
0,001 - 2,0 |
0,06·х + 0,00024 |
|
Неопентан |
0,0005 - 0,05 |
0,06·х + 0,00024 |
|
Гексаны (С6+) |
0,001 - 1,0 |
0,06·х + 0,00024 |
|
Гептаны (С7+) |
0,001 - 0,25 |
0,06·х + 0,00024 |
|
Октаны (С8+) |
0,001 - 0,05 |
0,08·х + 0,00022 |
|
Бензол |
0,001 - 0,05 |
0,08·х + 0,00022 |
|
Толуол |
0,001 - 0,05 |
0,08·х + 0,00005 |
|
Диоксид углерода |
0,005 - 10,00 |
0,06·х + 0,0012 |
|
Гелий |
0,001 - 0,5 |
0,06·х + 0,00024 |
|
Водород |
0,001 - 0,5 |
0,06·х + 0,00024 |
|
Кислород + Аргон |
0,005 - 2,0 |
0,06·х + 0,0012 |
|
Азот |
0,005 - 15 |
0,04·х + 0,0013 |
|
1) Расширенная абсолютная неопределенность U(x) в процентах при коэффициенте охвата k = 2 соответствует границе абсолютной погрешности при доверительной вероятности Р = 0,95. 2) Формула применяется при определении молярной доли метана по разности. 3) Формула применяется при измерении молярной доли метана впрямую. Примечание - Приведенные диапазоны значений молярной доли компонентов природного газа ограничены областью, для которой оценена неопределенность. Измерения молярной доли компонентов могут проводиться в более широких диапазонах, в этом случае неопределенность результатов измерений молярной доли компонентов может быть определена по формулам, приведенным в приложении А [21]. |
||
Таблица М.2 - Расширенная неопределенность для значений низшей и высшей теплоты сгорания природного газа
|
Теплота сгорания |
Диапазон значений теплоты сгорания Н |
Расширенная абсолютная неопределенность Uн |
|
Низшая теплота сгорания |
||
|
Молярная теплота сгорания, кДж·моль-1 |
От 765 до 803 включ. |
-0,017·Н + 14,8 |
|
Св. 803 до 1260 включ. |
0,0286·Н - 21,8 |
|
|
Объемная теплота сгорания, МДж·м-3 1) |
От 31,8 до 33,4 включ. |
-0,0124·Н + 0,46 |
|
Св. 33,4 до 52,5 включ. |
0,0285·Н - 0,905 |
|
|
Высшая теплота сгорания |
||
|
Молярная теплота сгорания, кДж·моль-1 |
От 840 до 891 включ. |
-0,0164·Н + 15,9 |
|
Св. 891 до 1440 включ. |
0,03·Н - 25,5 |
|
|
Объемная теплота сгорания, МДж·м-3 1) |
От 35,0 до 37,1 включ. |
-0,0121·Н +0,50 |
|
Св. 37,1 до 57,7 включ. |
0,03·Н - 1,06 |
|
|
1) Диапазоны значений объемной теплоты сгорания в МДж·м-3 рассчитаны по формуле (D.3) при р2 = 101,325 кПа и Т2 = 293,15 К. Примечание - Формулы для вычисления расширенной абсолютной неопределенности, приведенные в таблице М.2, справедливы: - при определении молярной доли метана по разности; - при суммарном значении молярной доли негорючих компонентов природного газа не более 3 % для диапазонов низшей теплоты сгорания от 33,1 до 34,3 МДж·м-3 (от 796 до 825 кДж·моль-1) и высшей теплоты сгорания от 36,7 до 38,1 МДж·м-3 (от 883 до 916 кДж·моль). |
||
Таблица М.3 - Расширенная неопределенность для значений плотности природного газа
|
Диапазон значений плотности природного газа, кг/м3 |
Диапазон значений теплоты сгорания |
Расширенная абсолютная неопределенность Up, кг/м3 |
|
Низшая теплота сгорания |
||
|
От 0,692 до 0,669 включ. |
От 765 до 803 кДж·моль-1 включ. |
0,0165·ρ - 0,0101 |
|
От 31,8 до 33,4 МДж·м-3 включ. |
||
|
Св. 0,669 до 1,210 включ. |
Св. 803 до 1260 кДж·моль-1 включ. |
0,0407·ρ - 0,0263 |
|
Св. 33,4 до 52,5 МДж·м-3 включ. |
||
|
Высшая теплота сгорания |
||
|
От 0,692 до 0,669 включ. |
От 840 до 891 кДж·моль-1 включ. |
0,0165·ρ - 0,0101 |
|
От 35,0 до 37,1 МДж·м-3 включ. |
||
|
Св. 0,669 до 1,210 включ. |
Св. 891 до 1440 кДж·моль-1 включ. |
0,0407·ρ - 0,0263 |
|
Св. 37,1 до 57,7 МДж·м-3 включ. |
||
|
Примечание - Формулы для вычисления расширенной абсолютной неопределенности, приведенные в таблице М.3, справедливы при определении молярной доли метана по разности. |
||
Приложение N
(обязательное)
Оценка неопределенности результатов определения теплоты сгорания, плотности и числа Воббе природного газа
N.1 Оценка расширенной неопределенности результата определения теплоты сгорания природного газа
При оценке неопределенности результата определения теплоты сгорания должны учитываться следующие составляющие:
- неопределенности измерений молярных долей компонентов природного газа;
- неопределенности табличных значений идеальной теплоты сгорания компонентов.
N.1.1 Оценка расширенной неопределенности результата определения теплоты сгорания природного газа при прямом измерении молярной доли метана
Оценку расширенной неопределенности результата определения идеальной теплоты сгорания ![]() природного газа вычисляют по формуле
природного газа вычисляют по формуле
|
|
(N.1) |
где
![]() - табличное значение идеальной теплоты сгорания
j-го компонента (раздел 10, таблицы 3-5);
- табличное значение идеальной теплоты сгорания
j-го компонента (раздел 10, таблицы 3-5);
![]() - значение идеальной теплоты сгорания природного газа, вычисленное по формуле (4) для молярной теплоты сгорания и по формулам (8) и (9) для объемной теплоты сгорания;
- значение идеальной теплоты сгорания природного газа, вычисленное по формуле (4) для молярной теплоты сгорания и по формулам (8) и (9) для объемной теплоты сгорания;
![]() - расширенная неопределенность ненормализованного значения молярной доли
j-го компонента, рассчитанная по формулам, приведенным в таблице М.1 (приложение М);
- расширенная неопределенность ненормализованного значения молярной доли
j-го компонента, рассчитанная по формулам, приведенным в таблице М.1 (приложение М);
xj - нормализованное значение молярной доли j-го компонента;
![]() - неопределенность табличного значения идеальной теплоты сгорания компонента, рассчитанная по формуле
- неопределенность табличного значения идеальной теплоты сгорания компонента, рассчитанная по формуле
|
|
(N.2) |
где ![]()
- расширенная относительная неопределенность для метана и этана составляет 0,1 %, для пропана - 0,2 %, для остальных компонентов - 0,3 % по [22].
N.1.2 Оценка расширенной неопределенности результата определения теплоты сгорания природного газа при определении молярной доли метана по разности
Оценку расширенной неопределенности результата определения идеальной теплоты сгорания ![]() природного газа вычисляют по формуле
природного газа вычисляют по формуле
|
|
(N.3) |
где
![]() - табличное значение идеальной теплоты сгорания
j-го компонента (раздел 10, таблицы 3-5);
- табличное значение идеальной теплоты сгорания
j-го компонента (раздел 10, таблицы 3-5);
![]() - табличное значение идеальной теплоты сгорания метана (раздел 10, таблицы 3-5);
- табличное значение идеальной теплоты сгорания метана (раздел 10, таблицы 3-5);
![]() - расширенная неопределенность значения молярной доли
j-го компонента, за исключением метана, рассчитанная по формулам, приведенным в таблице М.1 (приложение М);
- расширенная неопределенность значения молярной доли
j-го компонента, за исключением метана, рассчитанная по формулам, приведенным в таблице М.1 (приложение М);
xj - значение молярной доли j-го компонента;
![]() - неопределенность табличного значения идеальной теплоты сгорания компонента, рассчитанная по формуле (N.2).
- неопределенность табличного значения идеальной теплоты сгорания компонента, рассчитанная по формуле (N.2).
Примечание - Расширенную неопределенность результата определения теплоты сгорания реального газа принимают равной значению расширенной неопределенности результата определения теплоты сгорания идеального газа, так как:
- молярная и массовая теплота сгорания реального газа численно равны значениям молярной и массовой теплоты сгорания идеального газа (5.2 и 6.2);
- значение объемной теплоты сгорания реального газа рассчитывают, исходя из значения объемной теплоты сгорания идеального газа с учетом коэффициента сжимаемости, по формуле (10). В связи с тем, что значения коэффициентов сжимаемости отдельных компонентов природного газа известны с высокой точностью (раздел 10, таблица 2), составляющей неопределенности расчета коэффициента сжимаемости реального природного газа можно пренебречь (примечание 19).
N.1.3 Полученные значения расширенной абсолютной неопределенности результатов определения теплоты сгорания природного газа не должны превышать значений, рассчитанных по формулам, приведенным в таблице М.2 (приложение М).
N.2 Оценка расширенной неопределенности результата определения плотности природного газа
При оценке неопределенности результата определения плотности должны учитываться неопределенности измерений молярных долей компонентов природного газа. Неопределенностью табличных значений молярных масс компонентов из-за их незначительного вклада можно пренебречь.
N.2.1 Оценка расширенной неопределенности результата определения плотности идеального природного газа при прямом измерении молярной доли метана
Оценку расширенной неопределенности результата определения идеальной плотности Up природного газа вычисляют по формуле
|
|
(N.4) |
где
Mj - молярная масса j-го компонента (раздел 10, таблица 1).
N.2.2 Оценка расширенной неопределенности результата определения плотности идеального природного газа при определении молярной доли метана по разности
Оценку расширенной неопределенности результата определения идеальной плотности Up природного газа вычисляют по формуле
|
|
(N.5) |
где
Mj - молярная масса j-го компонента (раздел 10, таблица 1).
Примечание - расширенную неопределенность результата определения плотности реального газа принимают равной значению расширенной неопределенности результата определения плотности идеального газа, так как расчет реальной плотности природного газа проводят с учетом коэффициента сжимаемости по формуле (15) и вкладом составляющей неопределенности расчета коэффициента сжимаемости реального природного газа можно пренебречь (примечание 19).
N.2.3 Полученные значения расширенной абсолютной неопределенности результатов определения плотности природного газа не должны превышать значений, рассчитанных по формулам, приведенным в таблице М.3 (приложение М).
N.3 Оценка расширенной неопределенности значения числа Воббе
Оценку расширенной неопределенности значения числа Воббе Uw природного газа вычисляют по формуле
|
|
(N.6) |
где
Ud - расширенная неопределенность значения относительной плотности, рассчитанная по формуле
|
|
(N.7) |
где
d - значение относительной плотности, рассчитанное по формуле (11).
Приложение Р
(справочное)
Стандартные условия для проведения измерений и расчетов, принятые в разных странах
В таблице Р.1 приведены стандартные значения температуры, используемые при расчете теплоты сгорания и при приведении объема природного газа к стандартным условиям в различных странах мира по [23]. Значение стандартного давления для всех стран одинаково и составляет 101,325 кПа.
Таблица P.1
|
Страна |
Стандартная температура при расчете теплоты сгорания, °С |
Стандартная температура при приведении объема природного газа к стандартным условиям, °С |
|
Аргентина |
- |
151) |
|
Австралия |
15 |
15 |
|
Австрия |
25 |
0 |
|
Бельгия |
25 |
0 |
|
Бразилия |
- |
0 |
|
Канада |
15 |
15 |
|
Китай |
20 |
20 |
|
Чехия и Словакия |
25 |
20 и 0 |
|
Дания |
25 |
0 |
|
Египет |
- |
15 |
|
Финляндия |
- |
15 |
|
Франция |
0 |
0 |
|
Германия |
25 |
0 |
|
Гонконг |
- |
15 |
|
Венгрия |
- |
0 |
|
Индия |
- |
0 |
|
Индонезия |
- |
0 |
|
Иран |
- |
15 |
|
Ирландия |
15 |
15 |
|
Италия |
25 |
0 |
|
Япония |
0 |
0 |
|
Нидерланды |
25 |
0 |
|
Новая Зеландия |
- |
15 |
|
Норвегия |
- |
15 |
|
Пакистан |
- |
15 |
|
Румыния |
25 |
15 и 0 |
|
Россия |
25 |
20 и 0 |
|
Испания |
0 |
0 |
|
Швеция |
- |
0 |
|
Великобритания |
15 |
15 |
|
США |
15 |
15 |
|
Югославия |
0 |
0 |
|
1) 15°С соответствует 60°F. |
||
Библиография
|
Caulcutt R. and Boddy R. Statistics for Analytical Chemists, Chapman and Hall Ltd, London, (1983) |
|
|
IUPAC Commision on Atomic Weights and Isotopic Abudances, Atomic Weights of the Elements 1987. Pure Appl. Chem. 60 (6) pp. 842-854 (1988) |
|
|
Humphreys A.E., Some Thermophysical Properties of Components of Natural Gas and Cognate Fluids. Groupe Europeen de Recherchen Gazieres, Tech. Monograph No GERG TPC/1 (1986), 43 p. |
|
|
Cohen E.R. and Taylor B.N. The 1986 Adjustment of the Fundamental Physical Constants CODATA Bulletin No 63 (Nov. 1986) |
|
|
Giacomo P. Metrologia 18 (1982), pp. 33-40. |
|
|
Passut C.A. and Danner R.P. Ind. Eng. Chem. Proc. Des. Dev. 11 (4) (1972), pp. 543-546 |
|
|
ИСО 2533:1975 Стандартная атмосфера |
|
|
|
(ISO 2533:1975) (Standard atmosphere) |
|
Armstrong G.T. and Jobe T.L.jr. Heating Values of Natural Gas and its Components, US Dept. of Commerce, NBSIR 82-2401 (May 1982), 164 p. |
|
|
Garvin D., Domalski E.S., Wilhoit R.C., Somayajulu G.R. and Marsh K.N. Heating Values of Components of Natural Gas, Proc IGT Symposia on Natural Gas Energy Measurement, Chicago, Illinois (Aug. 1985 and April-May 1986), Elsevier Appl. Sci.Pub. London (1987), (eds. A. Attari and D.L. Klass), pp. 19-28 |
|
|
Garvin D., Domalski E.S., Wilhoit R.C., Somayajulu G.R. and Marsh K.N. Physical Properties of Pure Components of Natural Gas, Proc. 1st Int. Congress on Natural Gas Quality, (April 1986), Groningen. Elsevier Sci.Pub. b.v., Amsterdam (1986) (ed G.J. van Rossum), pp. 59-73 |
|
|
Wilhoit R.C. TRC Current Data News 3 (2) (1975), pp. 2-4 |
|
|
[12] |
Harmens A., Proc NPL Conf., Chemical Thermodynamic Data on Fluids and Fluid Mixtures |
|
Laughton A.P. and Humphreys A.E. Improvements in the Formulation of Ideal Gas Thermodynamic Properties for Natural Gas Applications, Proc, 4th Int. Gas Res. Conf., Tokyo (Nov. 1989) |
|
|
Mason D.McA. and Eakin B.E. Calculation of Heating Value and Specific Gravity of Fuel Gases, Institute of Gas Technology Res. Bull. № 32 (Dec. 1961), 18 p. |
|
|
Pitzer K.F. and Curl R.F.jr. The Volumetric and Thermodynamic Properties of Fluids, III Empirical Equation for the Second Virial Coefficient, J. Amer. Chem. 79 (1957), pp. 2369-2370 |
|
|
Gas Processors Association Standard GPA 2172-86:1986, Calculation of Gross Heating Value, Relative Density and Compressibility Factor for Natural Gas Mixtures from Compositional Analysis. 16 p. |
|
|
ГОСТ 20060-83 Газы горючие природные. Методы определения содержания водяных паров и точки росы влаги |
|
|
Rossini F.D., J.Res. NBS 6 (1931), pp. 37-49. J.Res. NBS 7 (1931), pp. 329-330 |
|
|
Pittam D.A. and Pilcher G. J. Chem. Soc. Faraday Trans. I 68 (1972), pp. 2224-2229; см. также Pittam D.A., M. Sc. thesis, University of Manchester (1971) |
|
|
LNG Measurement - A User's Manual for Custody Transfer (D. Mann, General Editor), US Dept of Commerce, NBSIR 85-3028 (1985), Section 1 |
|
|
ГОСТ 31371.7-2008 Газ природный, определение состава методом газовой хроматографии с оценкой неопределенности. Часть 7. Методика выполнения измерений молярной доли компонентов |
|
|
ГОСТ 30319.1-96 Газ природный. Методы расчета физических свойств. Определение физических свойств природного газа, его компонентов и продуктов его переработки |
|
|
ИСО 13443:1996 Природный газ. Стандартные условия |
|
|
|
(ISO 13443:1996) (Natural gas. Standard reference conditions) |
Ключевые слова: природный газ, теплота сгорания, плотность, относительная плотности, число Воббе, компонентный состав, точность, сходимость, воспроизводимость, неопределенность результатов определения высшей и низшей теплоты сгорания
| Расположен в: |
|---|
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/55790
На эту страницу сайта можно сделать ссылку:
На правах рекламы:
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|