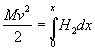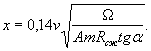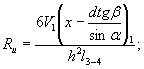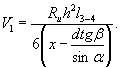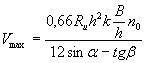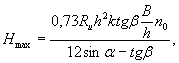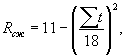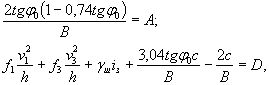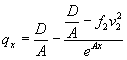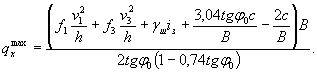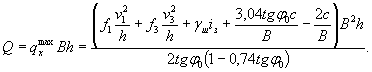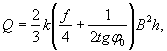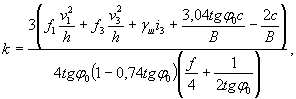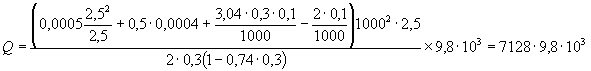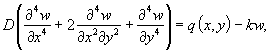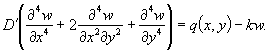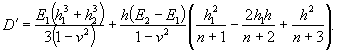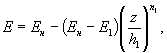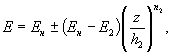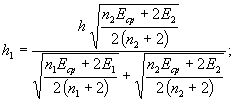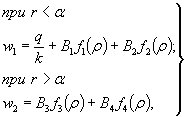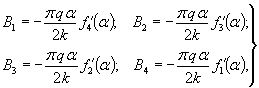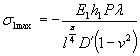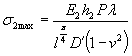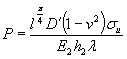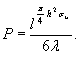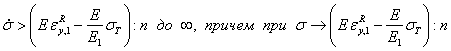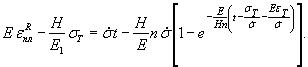
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"Труды Воздействие льда на опоры мостов и гидравлика сооружений. Труды Новосибирского института инженеров железнодорожного транспорта.ТРУДЫ НОВОСИБИРСКОГО ИНСТИТУТА ИНЖЕНЕРОВ ВЫПУСК 60 ВОЗДЕЙСТВИЕ ЛЬДА НА ОПОРЫ МОСТОВ
ИЗДАТЕЛЬСТВО «ТРАНСПОРТ» В сборнике освещаются результаты научных работ сотрудников кафедры «Гидравлика и водоснабжение» Новосибирского института инженеров железнодорожного транспорта в области воздействия льда на опоры мостов, борьбы с ледовыми затруднениями у водозаборов, использования несущей способности льда при сооружении мостов и причалов, а также гидравлики русел. Содержание ПРЕДИСЛОВИЕШирокое освоение восточных районов СССР, предусмотренное решениями XXII и XXIII съездов КПСС, вызвало к жизни строительство ряда железнодорожных линий в суровых климатических условиях Сибири и сооружение мостов через великие сибирские реки и участки создаваемых водохранилищ. В предлагаемом сборнике подведены итоги последних работ, выполненных сотрудниками кафедры «Гидравлика и водоснабжение» НИИЖТа в области воздействия льда на опоры мостов, борьбы с ледовыми затруднениями у водозаборов, использования несущей способности льда при сооружении мостов и причалов. В сборник включены также две работы, посвященные гидравлике русел под ледяным покровом и методам гашения энергии в отводящих руслах малых мостов и труб. В статьях проф. К.Н. Коржавина обосновываются предложения к проекту новых норм на ледовые нагрузки на опоры мостов и даются рекомендации по расчету опор мостов на ледовые воздействия в условиях водохранилищ. Статьи доцентов В.М. Самочкина, Г.Я. Кузуба и инж. В.К. Тройнина освещают особенности образования зажоров на реках Сибири, ледовые затруднения, возникающие в нижних бьефах ГЭС, и выдвигают новые приемы учета воздействия зажорных масс на опоры мостов. В статьях проф. К.Н. Коржавина, старшего научного сотрудника А.Е. Якунина и младшего научного сотрудника Ф.И. Птухина рассмотрены вопросы использования несущей способности ледяного покрова для строительства мостов и причалов с учетом анизотропии ледяного покрова и скорости нагружения. Статьи доц. И.К. Поклонского и инж. У.С. Рось излагают результаты исследования в области гидравлики потока под ледяным покровом и способов гашения энергии в отводящих руслах малых искусственных сооружений. Ректор института проф. Н. КОНДАКОВ Проф. д-р техн. наук К.Н. КОРЖАВИНОБОСНОВАНИЕ ПРОЕКТА НОВЫХ НОРМ ПО УЧЕТУ ЛЕДОВЫХ НАГРУЗОК НА ОПОРЫ МОСТОВШирокое развитие транспортного строительства в восточных районах страны требует более внимательного отношения к учету возможных ледовых нагрузок на сооружения и особенно па опоры мостов, находящихся в более тяжелых условиях по сравнению с массивными гидротехническими сооружениями. Суровые климатические условия значительной части СССР приводят к образованию ледяного покрова большой толщины. Меридиональное направление многих крупных рек Сибири (Иртыша, Оби, Енисея, Лены и др.) обусловливает сравнительно тяжелые условия весеннего ледохода, характерного прочным льдом, заторами, значительными скоростями движения крупных ледяных полей. Широкое применение прогрессивных сборных конструкций опор требует исследования их работы на ледовые воздействия. Особого внимания заслуживают опоры мостов, расположенных в зоне крупных водохранилищ. Из-за значительной высоты таких опор резко повышается влияние ледовых нагрузок, учет которых существенно утяжеляет сборную конструкцию. Оценка существующих норм Методы оценки ледовых нагрузок на опоры мостов несколько раз изменялись за последние 20 лет. Технические условия проектирования железнодорожных мостов (ТУПМ-47) предусматривали неоправданно высокий предел прочности льда (100-200 т/м2), не учитывали явления местного смятия, наблюдающегося при контакте ледяного поля с опорами моста, очень грубо оценивали роль опоры в плане и исходили из ошибочной схемы при учете воздействия льда на опоры с наклонной гранью. Более поздние нормы ТУПМ-56, основанные на исследование А.И. Гамаюнова, форму опоры в плане оценивали тоже приближенно, не учитывали явления местного смятия и исходили из теории деформации упругой изотропной пластины на упругом основании, что мало соответствовало действительной картине явления. Выявилось большое несоответствие между фактической величиной давления и требованиями ТУПМ-56, которые дают значительно заниженные величины давления для опор с наклонными гранями и сильно завышенные для опор с вертикальными гранями [1]. Действующие технические условия проектирования мостов СН 200-62 оценивают динамическое давление льда более обоснованно. На основании исследований ряда авторов [1, 2, 3] существенно снижены расчетные пределы прочности льда сжатию и изгибу, введен учет явления местного смятия, неполноты соприкасания опоры и льдины, детально оцениваются форма опор в плане. Давление на наклонные опоры учитывается на основе серьезных разработок Б.В. Зылева [4]. Однако исследования, проведенные в Транспортно-энергетическом институте Сибирского отделения Академии наук СССР (ТЭИ), на кафедре гидравлики НИИЖТ, во ВНИИГ им. Б.Е. Веденеева, Государственном гидрологическом институте (ГГИ) и другими организациями, позволяют в настоящее время внести новые предложения по улучшению действующих норм. Эти предложения в части оценки давления на опоры мостов в основном сводятся к следующему: 1. Формула норм Госстроя СССР СН 76-59 и основанных на них рекомендациях СН 200-62 имеет вид
и дает величину максимального возможного давления крупных ледяных полей на опоры. Предполагается, что опора врезается в ледяное поле на полную свою ширину (В) и испытывает максимально возможное давление, возникающее при разрушении ледяного покрова в зоне контакта. В некоторых случаях возможные размеры льдин не позволяют рассчитывать на такие силы взаимодействия. Льдины меньших размеров (по исследованиям [1] площадью менее 10 тыс. м2), исчерпав запас кинетической энергии на разрушение своей кромки, будут останавливаться или раскалываться. Силы взаимодействия при этом будут меньшими, что нужно отразить в нормах. 2. Расчленение обширной территории СССР всего на две зоны, для которых рекомендуются различные пределы прочности льда, слишком грубо. В настоящее время есть достаточно обоснованные данные для разделения территории на большее количество зон. 3. Зависимость, предложенная для определения динамического давления льда на опоры мостов с наклонной гранью (см. СН 76-59 или приложение 12 к СН 200-62),
совершенно не учитывает влияние ширины опоры, т.е. исходит из предположения, что ледяное поле раскалывается раньше, чем опора внедрится в лед на полную свою ширину. Наблюдения на реках Сибири [1, 5] показывают, что это не так и влияние ширины опоры на силы взаимодействия несомненно и должно быть учтено. 4. Рекомендации для выбора расчетного предела прочности льда для опор с наклонными ледорезами в СН 76-59 и СН 200-62 завышены и могут быть уменьшены. 5. Действующие нормы недостаточно подробно освещают условия работы опор, расположенных в условиях водохранилищ. Эти условия существенно отличаются от речных и должны быть выделены в нормах отдельным параграфом. 6. Действующие нормы не дают конкретных указаний для оценки воздействия заторных и зажорных масс на опоры мостов. Однако такие случаи бывают и количественная оценка ледовых нагрузок крайне необходима. Предложения по проекту новых норм Оценка усилий, возникающих при прорезании вертикальной опоры крупного ледяного поля. Для оценки можно предложить формулу, отличающуюся от формулы (1) только введением климатического коэффициента А, более детально учитывающего физико-географические особенности района, т.е.
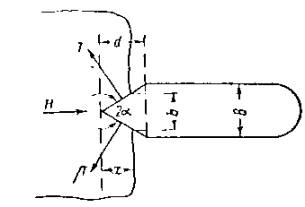
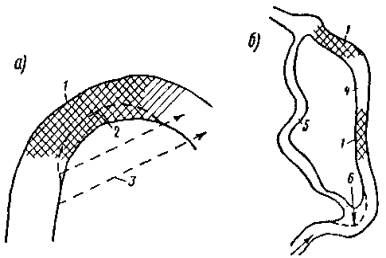
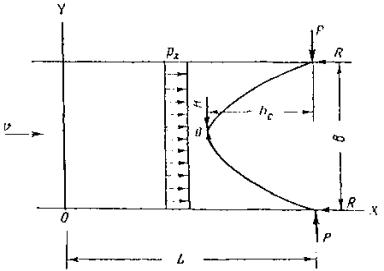
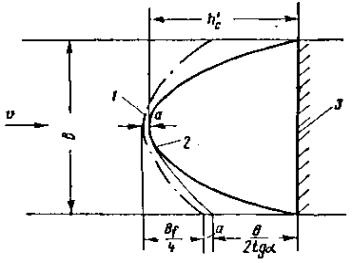
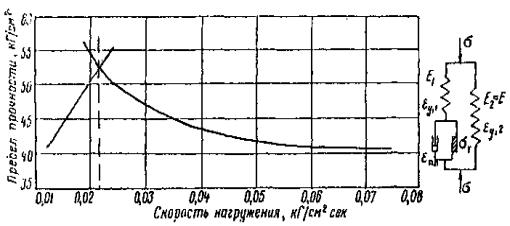
Оценка усилий, возникающих при ударе ледяного поля о вертикальную опору с последующей его остановкой. Рассмотрим случай, когда ледяное поле площадью Ω и толщиной h движется со скоростью v по направлению к мостовой опоре, имеющей заостренное очертание в плане, с углом заострения 2α (рис. 1). Рис. 1. Схема разрушения ледяного покрова вертикальной опорой Давление льда на опору может быть определено по зависимости
где Fсм - площадь соприкасания льдины и опоры в данный момент времени; Rcм - предел прочности льда (при раздроблении) с учетом явления местного смятия; m - коэффициент формы опоры; им учитывается, что для опоры более острых очертаний требуется меньшее усилие [1]. Принимая ширину площадки смятия в данный момент равной b = 2xtgα, находим возможное давление
Так как при массивных опорах запас энергии ледяного поля в основном расходуется на разрушение его кромок, то из сопоставления
находим наибольшую глубину внедрения (в момент остановки ледяного поля), равную
Подставляя значение х в выражение (5), находим
Если учесть, что при воздействии на вертикальную опору возможно местное смятие и в предыдущих формулах введен расчетный предел прочности с учетом местного смятия (Rр = = 2,5Rсж), то можно пользоваться и формулой
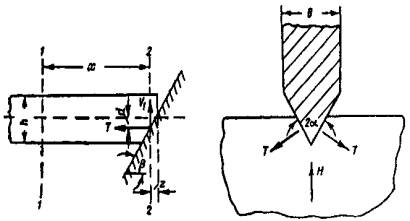
Расчетное динамическое давление на опору с вертикальной гранью. По-видимому, за расчетное динамическое давление на опору с вертикальной гранью следует принять наименьшее из давлений, определенных по формулам (3) и (7) или (8). В самом деле, если H2 < H1 то льдина остановится у опоры, оказывая давление H2. Прорезание льдины опорой отсутствует. Если H1 < H2, то льдина будет прорезаться опорой при максимально возможном давлении Н1. Давление, возникающее при прорезании крупного ледяного поля опорой с наклонной режущей гранью. Исследованиями [1] подтверждается возможность учета влияния ширины опоры в рассматриваемом случае. Напомним процесс разрушения крупного ледяного поля. При встрече с сооружением, снабженным наклонной ледорезной гранью, происходит смятие острой кромки льдины (рис. 2), сопровождающееся появлением реакции опоры, которую можно разложить на составляющие V1 и T, связанные между собой зависимостью
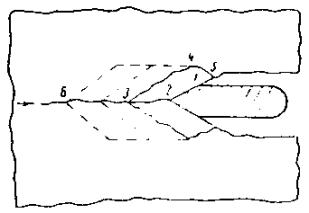
Под действием сил V1 и Т возможно разрушение льдины от изгиба в сечении 1-1 на расстоянии у от опоры или среза в сечении 2-2. Кроме того, возможно разрушение льдины от раздробления под действием сил Т или же их равнодействующей
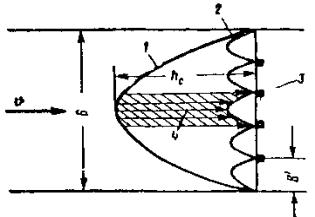
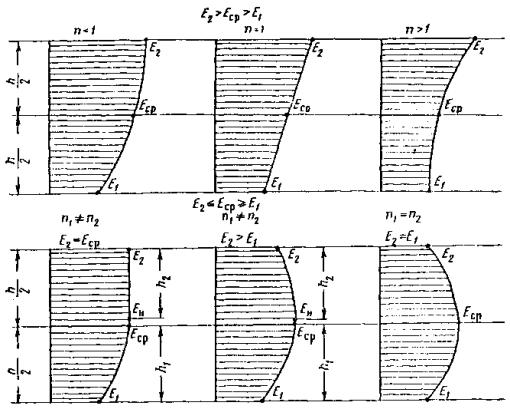
Очевидно, что разрушение произойдет по той схеме, при которой напряжение изгиба, среза или раздробления ранее всего достигнет предельного значения. Можно предположить, что ледяной покров, сильно потерявший свою прочность, разрушится от напряжений среза. Более или менее прочный ледяной покров будет разрушаться путем изгиба. При крутых ледорезах возможно разрушение от раздробления, когда вертикальная составляющая реакция опоры V1 невелика. Рис. 2. Схема разрушения ледяного покрова наклонной опорой Так как применение крутых ледорезов (с углом более 80°) нерационально (разрушение происходит от раздробления, как и при опорах с вертикальным ледорезом, и применение наклонной грани не оправдано), а разрушение слабых льдин от среза не может явиться расчетным, то следует подробнее рассмотреть случай разрушения ледяного поля путем изгиба. Физическая картина явления в этом случае следующая. Встречаясь со льдиной, массивная опора врезается на более или менее значительную величину, равную n0l и несколько меньшую длины режущей грани опоры l. После врезания и смятия кромки льдины опора воздействует на ледяное поле (рис. 3) своими боковыми гранями 1-2, стремящимися приподнять ледяное поле. Рис. 3. Воздействие льда на наклонную опору моста При этом наблюдается смятие нижней кромки льда на величину z (см. рис. 2), в связи с чем реактивное давление опоры на льдину можно разложить на составляющие V1 и Т, связанные между собой зависимостью
В этом выражении β1 - угол наклона боковых граней режущего ребра к горизонту, связанный с углом наклона режущего ребра (см. рис. 2) выражением [1] Под воздействием сил V1 и Т происходит излом ледяного поля, сопровождающийся появлением не менее трех опережающих трещин, выделяющих две полосы льда, от которых затем отламываются карты льда 2-3-4-5 (см. рис. 3). После этого давление на опору падает, трещины 3-2 и 4-5 смыкаются и льдина продолжает двигаться вперед, не испытывая серьезного противодействия до тех пор, пока опора снова не войдет в контакт с ней по линии 3-4 и явление не повторится. Таким образом, результирующее давление на льдину сводится к двум силам: V = 2V1 и H = 2Tsinα. Учитывая выражения (11) и (12) и вводя по Б.В. Зылеву коэффициент 1,1, учитывающий трение между опорой и льдиной, находим
Глубокого смятия кромки льдины обычно не происходит. Следовательно, силы V1 и Т приложены ближе к нижней поверхности льда, как показано на рис. 2. Таким образом, процесс разрушения ледяного покрова весьма сложен, начиная с образования опережающих трещин; давление носит периодический характер с колебанием от максимального до минимума, приближающегося к нулю. Размеры опоры и ее форма по существу определяют характер явления и, безусловно, должны учитываться при расчете. Расчетные зависимости рассмотрим на примере массивной опоры, прорезающей крупную льдину наклонным ребром ледореза с треугольным очертанием режущей грани в плане (по схеме рис. 3). Давление на кромку ледяного поля по длине 1-2 приводит к выделению ледяной консоли с последующим изломом по линии 3-4 на некотором расстоянии от опоры. Можно принять, что излом происходит по линии 3-4 приблизительно длиной
Здесь n0 - коэффициент, меньший единицы, учитывающий форму опоры в плане. Вероятно, что при острых очертаниях режущей грани излом может начинаться еще до того, как опора врезалась в льдину на полную ширину. Так как ширина выделенной карты льда обычно не более 3-5 м, то можно рассматривать полосу 2-3-4-5 как консоль, защемленную в сечении 3-4 и находящуюся под воздействием сил V1 и Т. Собственный вес консоли уравновешивается гидростатическим давлением и, так как выход льдины из воды перед изломом весьма невелик, может не учитываться. Тогда изгибающий момент в сечении 3-4 M = V1x - Td, или с учетов зависимостей (11) и (12)
Момент сопротивления
наибольшее напряжение в сечении 3-4 к моменту излома может быть определено по выражению
На основании многолетних натурных наблюдений за работой опор мостов и гидросооружений [1, 5, 6, 7] можно установить, что излом ледяных полей наблюдается на расстоянии 2,5-6 толщин льда. Очевидно, что меньшему значению плеча соответствует большее значение силы V1, ломающей лед. С некоторым запасом можно принять x = 3h. Величина плеча d горизонтальной составляющей H может колебаться от 0 до 0,5 h, составляя в среднем 0,25 h. Отсюда,
принимая х = 3h; d
= 0,25h;
наибольшее горизонтальное давление па опору
или
где коэффициент формы опоры при изгибе равен
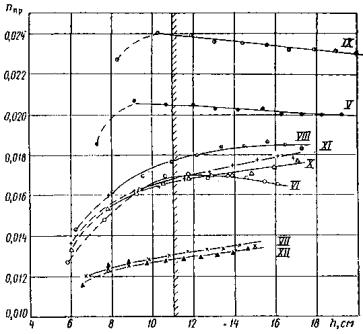
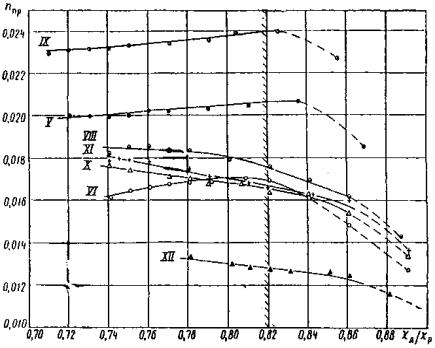
Численное значение коэффициента S0 определим следующим образом. Для вертикальной опоры величина давления льда может быть подсчитана по формуле
следовательно, влияние формы отражено произведением
где Б - коэффициент пропорциональности. Учитывая, что [1]
найдем при
Сопоставление результатов подсчета с опытными данными [1] дает возможность принять величину Б примерно равной 2. Тогда значения коэффициентов формы опоры могут быть подсчитаны по зависимости (21) для заданных конкретных условий (см. ниже таблицу в разделе «Предлагаемый вариант новых норм»). Как видим, влияние угла заострения 2α сравнительно сильно сказывается лишь при меньших его значениях. Некоторый рост усилий Н при очень малых углах заострения может быть объяснен тем, что более острая опора быстрее внедряется в лед и в связи с этим длина карт льда, выламываемых ледорезом, соответственно увеличивается (рис. 4). Таким образом, максимальное давление может быть определено по формуле (20), которую и рекомендуется ввести в нормы.
Рис. 4. Схемы разрушения ледяного покрова в зависимости от формы опоры в плане Расчетная прочность льда. Рекомендуемые СН 76-59 и СН 200-62 пределы прочности льда при раздроблении достаточно правильно характеризуют условия, наблюдающиеся при вскрытии рек СССР. Значения же предела прочности для определения ледовых нагрузок на опоры с наклонной гранью завышены вследствие допущенной неточности: расчетный предел прочности льда при раздроблении принят с учетом местного смятия, который отсутствует при изломе ледяного поля на режущей грани наклонного ледореза. Поэтому вполне возможно снизить расчетный предел прочности при учете давления на опоры с наклонной гранью. Так как в нормах СН 76-59 и СН 200-62 учтен также коэффициент неплотности соприкасания опоры и льдины, равный 0,75, то предел прочности изгиба может быть принят равным
т.е. приближенно
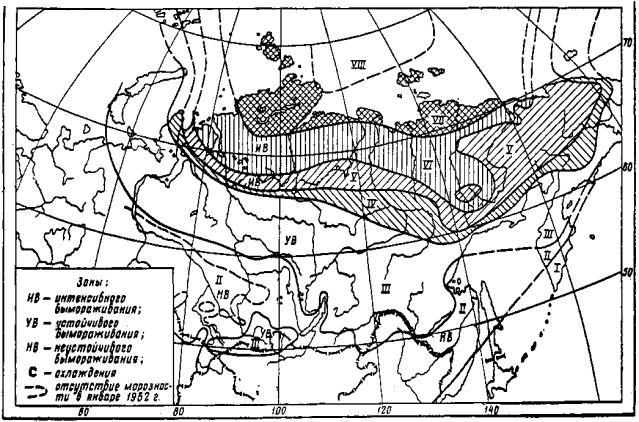
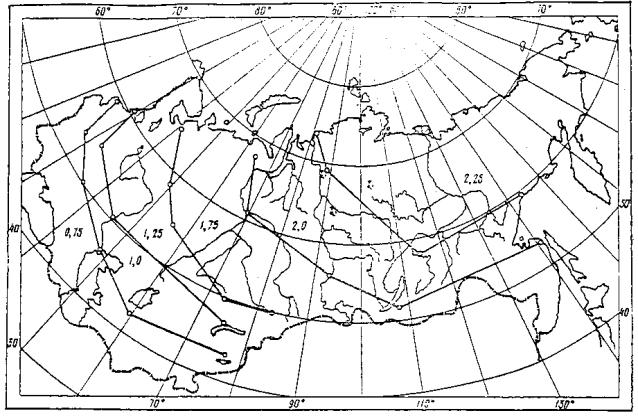
Значения климатического коэффициента. Как сказано выше, совершенно недостаточно разделение громадной территория СССР всего на две зоны по условиям силы весеннего ледохода. Целесообразнее ее разделить на большее число зон с различным значением климатического коэффициента А. Эта задача может быть решена лишь с известной степенью приближения и дальнейшим уточнением. Проанализировав предложения М.М. Крылова [8], данные УГМС о метеорологической обстановке в период вскрытия рек СССР, карту морозности СССР (рис. 5), можно предложить значения коэффициента А, приведенные на рис. 6. Несомненно, границы между зонами в будущем должны корректироваться, хотя предлагаемые значения коэффициентов А на данный период достаточно обоснованы.
Рис. 5. Схематическая карта зон морозности Сибири и Дальнего Востока с температурой воздуха ниже -15°С по зоне: I - до 40 суток в году; II - от - 41 до 110; III - от 111 до 150; IV - от 151 до 160; V - от 161 до 170; VI - от 171 до 180; VII - от 181 до 190; VIII - от 191 до 200
Рис. 6 Карта климатического коэффициента А Цифрами показана числовая величина коэффициента для шести территориальных участков Оценка воздействия льда при заторных и зажорных явлениях. В настоящее время решение этого важного вопроса только намечается. Обоснованные рекомендации для включения в общественные нормы трудно предложить. Сложность процесса образования заторов и зажоров и крайне тесная связь их с местными физико-географическими и метеорологическими условиями не позволяет предложить бесспорные пригодные для всех случаев нормы. Разработка этого вопроса в НИИЖТе [9] позволяет рекомендовать для количественной оценки величины возможных сил взаимодействия формулу (1) настоящей статьи при значениях Rр =0,50 ÷ 0,66 предела прочности речного льда и hл = 3 ÷ 4 толщины льда, образовавшегося к расчетному периоду, по не более 0,8 глубины на прилегающем участке реки. Климатический коэффициент А возможно применять в пределах от 0,75 до 1,25 [9]. Более подробно эти вопросы опубликованы в работах [9, 11]. Работа опор в условиях водохранилищ Неблагоприятные условия работы опор мостов на водохранилищах - значительная высота их (до 30-50 м) при учете ледовых воздействий - приводит к утяжелению конструкции и повышению стоимости моста. Исследование этого вопроса [10] позволяет сделать следующие выводы: 1. Наиболее вероятная расчетная схема сводится к определению возможных давлений по формулам (3) и (7). 2. Наибольшее давление возникает при ветровом нагоне крупного ледяного поля на сооружение. Учитывая, что дрейф ледяных полей возможен лишь при наличии разводни, расчетный предел прочности льда не должен превышать 30-50 т/м2. 3. Скорость дрейфа ледяного поля можно определять по формуле
где W - скорость ветра, принимаемая в зависимости от площади льдины по рекомендациям, опубликованным в трудах [1, 10]. Расчетная площадь льдины определяется на основании анализа местных условий, а при отсутствии достаточно надежных данных - исходя из принятой разбивки отверстия моста на пролеты [10]. ПРЕДЛАГАЕМЫЙ ВАРИАНТ НОВЫХ НОРМ Учитывая высказанные соображения, можно предложить следующую редакцию новых норм по оценке ледовых воздействий на опоры мостов. 1. Общие положения 1. Настоящими техническими условиями следует руководствоваться при определении ледовых нагрузок на опоры речных гидротехнических сооружений и мостов. При проектировании гидротехнических сооружений I класса и больших мостов в сложных ледовых условиях ледовые нагрузки, определенные согласно настоящим техническим условиям; рекомендуется уточнять на основе более длительных натурных наблюдений. При проектировании речных гидротехнических сооружений и мостов нужно учитывать следующие ледовые нагрузки и воздействия на сооружения: - динамическое давление льда при ударе свободно плывущих льдин; - динамическое давление заторных масс льда; - статическое давление сплошного ледяного покрова при его термическом расширении; - статическое давление свободно плавающего ледяного поля при навале (под влиянием ветра или течения); - воздействие примерзшего к сооружению ледяного покрова (при колебании уровня воды); - истирающее воздействие льдин на поверхность сооружения при движении льдин под влиянием ветра, течения или колебания уровня воды. Ледовые нагрузки и воздействия не учитываются, если на основе технико-экономических расчетов предусмотрены специальные эффективные меры для предотвращения ледовых воздействий и давления льда на сооружения. 2. Настоящими техническими условиями определяются нормативные пределы прочности и величины давления льда. Коэффициент перегрузки n для ледовой нагрузки принимается по действующим техническим условиям на соответствующие сооружения. 3. При расчетах конструкций гидротехнических сооружений по методу разрушающих усилий расчетная ледовая нагрузка принимается равной нормативной. 2. Определение ледовых нагрузок и воздействий. Опоры (быки) с вертикальными гранями 4. Давление льда Н1 в тоннах на опору в направлении вдоль ее оси, возникающее при прорезании его сплошного ледяного поля, определяется по формуле
Давление льда Н2 в тоннах на опору в направлении вдоль ее оси, возникающее при воздействии льдины и последующей ее остановке, подсчитывается по формуле 5. За расчетную величину давления принимается наименьшая из подсчитанных по формулам (1*) и (2*). В этих формулах приняты обозначения: h - толщина льда, принимаемая равной 0,8 наибольшей за зимний период толщины 1 % обеспеченности, м; В - ширина опоры на уровне ледохода, м; m - коэффициент формы опоры, принимаемый равным: для полуциркульного очертания ледореза - 0,9; для треугольной формы ледореза - независимо от величины радиуса закругления его носовой части в зависимости от угла 2α заострения ледореза в плане.
* Здесь и далее нумерация формул со звездочкой дана в отличие от предыдущей с тем же номером. Rр - предел прочности льда при раздроблении с учетом явления местного смятия льда; при отсутствии экспериментальных данных принимается (на уровне начальной стадии ледохода) равным 75 т/м2, а при наивысшем уровне ледохода - равным 45 т/м2; Ω - площадь ледяного поля по данным полевых наблюдений или по аналогии с другими объектами, м2 Ωmin = 1,75l2 l - наибольшая величина пролета прилегающего к опоре моста или ледосбросного отверстия; v - скорость движения льдины, принимаемая: для рек и проточных водоемов - равной скорости течения, а для больших водохранилищ - равной скорости ветрового нагона льда; определяется па основе анализа гидрометеорологической обстановки с учетом конфигурации водохранилища, но не более 0,6 м/сек; А - климатический коэффициент, принимаемый равным: Южнее линии Таллин - Минск - Харьков - Астрахань - Нукус - Алма-Ата - 0,75 Южнее линии Выборг - Смоленск - Камышин - Балхаш - 1,00 Южнее линии Архангельск - Киров - Уфа - Караганда - Усть-Каменогорск - 1,25 Южнее линии Воркута - Ханты-Мансийск - Красноярск - Улан-Удэ - Николаевск-на-Амуре - 1,75 Южнее линии Диксон - Норильск - Бодайбо - Охотск - 2,00 Севернее линии Диксон - Норильск - Бодайбо - Охотск - 2,25 При проектировании ответственных сооружений климатический коэффициент может приниматься на основании оценки условий вскрытия по данным натурных наблюдений. Опоры (быки) с наклонными ледорезами 6. При определении давления льда на опору в направлении ее оси горизонтальная составляющая давления H3 в тоннах принимается по формуле
7. Вертикальная составляющая давления V и тоннах определяется по формуле
где Rиз - предел прочности льда при изгибе, принимаемый без учета местного смятия равным 0,5Rр, т/м2; β - угол наклона режущего ребра к горизонту, град; A, h - по рекомендации п. 5; S0 - коэффициент формы опоры, принимаемый по таблице.
8. Горизонтальная составляющая давления Н3 не должна превышать величины, подсчитанной по формуле (1*). 9. При несовпадении направления движения льдин с осью опоры давление льда на вертикальные грани опоры от удара одиночных льдин определяется по формуле п. 10. 10. Наибольшее давление определяется по формуле
где k - коэффициент неплотности соприкасания ледяного поля и сооружения, принимаемый равным 0,6-0,8 (соответственно для начальной стадии ледохода и наивысшего уровня ледохода); Rсж - предел прочности льда сжатию без учета местного смятия, принимаемый в начальный период ледохода 50 т/м2, а при наивысшем горизонте - 30 т/м2. 11. Опоры мостов через водохранилища. Наибольшее давление, возможное при встрече мостовой опоры с дрейфующим ледяным полем, может быть определено по формуле (1*) или (2*) при следующих значениях расчетных параметров: - предел прочности льда в период высокого ледохода Rр = 45 т/м2; - климатический коэффициент для всех районов СССР A = 1,00; - расчетная скорость дрейфа ледяных полей определяется в зависимости от скорости ветра и площади ледяного поля
но не более 0,6 м/сек; - расчетная скорость ветра W принимается с учетом расчетной площади льдины Ω
- W уточняется на основе детального анализа местных физико-географических и метеорологических условий; - расчетная площадь льдины определяется по данным полевых наблюдений, но не может быть меньше Ωmin = 1,75l, где l - наибольшая величина пролета, прилегающая к опоре моста. ЛИТЕРАТУРА 1. Коржавин К.Н. Воздействие льда на инженерные сооружения. Издание СО АН СССР. Новосибирск, 1962. 4. Зылев Б.В. Давление льда па наклонные ледорезы. Труды МИИТа, вып. 74. М., 1950. 5 Коржавин К.Н. Работы ледорезов мостовых опор в условиях ледохода сибирских рек. Труды НИВИТа, вып. III. Томск, 1938. 8. Крылов М.М. Ледяные изотермические склады. Изд. АН СССР, М., 1951. Проф. д-р техн. наук К.Н. КОРЖАВИНК ВОПРОСУ ОБ УЧЕТЕ ВОЗДЕЙСТВИЯ ЛЬДА НА ОПОРЫ МОСТОВ ЧЕРЕЗ УЧАСТКИ ВОДОХРАНИЛИЩ НА РЕКАХ СИБИРИШирокое развертывание транспортного и гидроэнергетического строительства в Сибири требует детального учета воздействия льда на речные сооружения и, в частности, на опоры мостов, сооружаемых в пределах водохранилищ. Такие опоры часто имеют весьма значительную высоту (до 30-50 м), в связи с чем учет воздействия льда по требованиям СН 76-59 или СН 200-62 существенно утяжеляет их конструкцию. Реальная оценка возможных ледовых нагрузок осложнена и тем, что особенности ледового режима водохранилищ не нашли достаточно подробного освещения в нормативных указаниях и транспортной литературе. Некоторые особенности льдотермического режима водохранилищ Натурные исследования, поставленные Транспортно-энергетическим институтом Сибирского отделения Академии наук СССР, кафедрой гидравлики НИИЖТа, Государственным гидрологическим институтом, обсерваториями УГМС, экспедициями Гидропроекта и другими учреждениями на водохранилищах Союза ССР, позволили установить, что создание водохранилищ существенно изменяет ледотермический режим рек. Можно отметить следующие особенности. В связи с резким уменьшением скоростей течения замерзание водохранилищ происходит в более ранние сроки по сравнению с незарегулированными условиями. На водохранилищах Сибири различие в сроках ледостава может достигать 10-15 суток, а иногда и более. Вследствие изменений условий замерзания (более спокойный характер ледостава, меньший объем зашугованности водоема и отсутствие подвижек при замерзании) ледяной покров водохранилищ имеет на большинстве участков однородное сравнительно правильное кристаллическое строение по всей толщине. Отмечается и более равномерное распределение толщины льда на площади водохранилища по сравнению с речными условиями. Как показали длительные наблюдения на Новосибирском водохранилище [1, 2, 3], толщина покрова на сравнительно неглубоких водоемах (порядка 20 м) существенно не отличается от речных условий. Это является результатом взаимодействия двух тенденций. Уменьшение скоростей течения способствует образованию более толстого ледяного покрова, как это и наблюдается при сопоставлении рек с озерами. С другой стороны, интенсивность роста толщины ледяного покрова снижается притоком тепла, аккумулируемого в глубоких водоемах, а также за счет более спокойного замерзания, как это убедительно показано И.Я. Лисером на примере р. Енисея [4]. Толщина ледяного покрова на глубоких водохранилищах (типа Братского) может быть даже и меньше, чем в речных условиях, за счет влияния тепла, аккумулированного в водоеме. По сообщению руководителя Братской обсерватории УГМС Л.Н. Быдина толщина ледяного покрова на водохранилище в зиму 1964/65 г. не превышала 0,6-0,8 м, что даже меньше толщин льда, наблюдавшихся в этом районе на Ангаре [5]. Таким образом, при прогнозировании расчетной толщины льда после создания водохранилищ нужно учитывать глубину водоема и при глубинах более 15-20 м не назначать расчетную толщину льда больше наблюденной в речных условиях; при глубинах порядка 5-8 м можно ожидать несколько большую (на 15-20 %) толщину льда. Ледяной покров водохранилищ имеет обычно много трещин термического происхождения. Их количество заметно увеличивается после резких похолоданий и при отсутствии снега на льду. Трещины имеют ширину до 1-2 см, расположены через 10-25 м и через 5-6 суток обычно смерзаются [18]. Смерзшиеся трещины заметно не понижают прочности ледяных полей, которые в весенний период часто раскалываются не по направлению трещин [6]. Особенности строения ледяного покрова водохранилищ определяют и своеобразный характер его разрушения. Решающая роль здесь принадлежит радиационному теплоприходу. После схода снегового покрова с поверхности льда (по наблюдениям И.П. Бутягина) наиболее быстро разрушаются весной участки с правильным кристаллическим строением, которые преобладают в ледяном покрове водохранилищ. В результате таяния межкристаллических прослоек наблюдается более или менее интенсивное (в зависимости от местных гидрометеорологических условий данной весны) разделение ледяного покрова па кристаллы и их группы, иногда по всей толщине. Разрушительное воздействие солнечной радиации усиливается притоком тепла из воды, имеющей в водохранилищах более высокую температуру, чем в речных условиях. Как показали измерения на р. Оби, температура воды, сбрасываемой из водохранилища в нижний бьеф Новосибирской ГЭС, с января по май не опускалась ниже 0,6°С, а в апреле была в среднем около 1°С. Существенное падение прочности льда с разделением его на кристаллы отмечается в сроки более ранние, чем подвижки льда в незарегулированных участках. Как указывает И.П. Бутягин [2], в 1958-1960 гг. полное разделение ледяного покрова на кристаллы в низовом участке Новосибирского водохранилища наблюдалось на 1-7 дней ранее начала ледохода в створе у г. Камня. Таким образом, прочность ледяных полей, действующих на опоры мостов в районе водохранилищ, должна приниматься меньшей, чем в речных условиях. Задержка вскрытия водохранилища по сравнению с речными условиями (на 10-12 суток) приводит к тому, что пределы прочности льда изгибу и сжатию заметно снижаются (в 1,5-2 раза) по сравнению с прочностью, наблюдавшейся к началу весеннего потепления. Представляют интерес результаты определений предела прочности льда сжатию и изгибу, проведенные перед вскрытием Новосибирского водохранилища [6] и Енисея у г. Красноярска [7] при температуре льда около 0°С, приведенные в таблице.
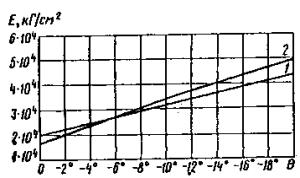
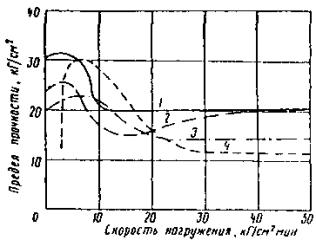
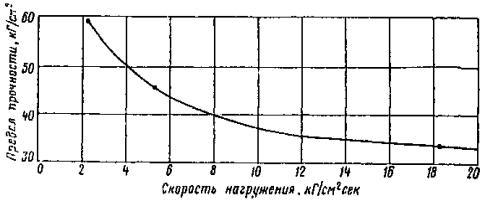
Так как вскрытие водохранилищ происходит с запозданием на 10-15 суток, а для возможности дрейфа льда необходимы пространства чистой воды (разводья), то предел прочности льда, вероятно, будет даже меньше величии, указанных в таблице. Если учесть, что при внедрении опоры в ледяное поле возникает эффект местного смятия [1], увеличивающий предел прочности раза в два, то расчетное давление может быть принято равным 40-50 т/м2. Динамика падения прочности ледяного покрова сжатию или изгибу (по исследованиям на Новосибирском водохранилище это весьма близкие величины) может по предложению Ф.И. Быдина, откорректированному для Сибири И.П. Бутягиным [6], определяться по выражению
где Rсж - предел прочности сжатию, кг/см2; åt - сумма среднесуточных положительных температур воздуха (с начала потепления), °С. В условиях водохранилища малые скорости течения не обеспечивают нормального ледохода. Ледяной покров тает на месте, но может дрейфовать по акватории водохранилища под влиянием ветра. При встрече дрейфующего ледяного поля опора моста испытывает существенное давление, которое приводит к повреждениям и разрушениям. Подобные случаи известны как в СССР, так и за рубежом. А.С. Ольмезов и Г.С. Шпиро [9, 1] описали случай серьезных повреждений ряда опор моста, строившегося па юге европейской части СССР. Крупное ледяное поле, принесенное течением и ветром, подошло к мосту со скоростью 0,3-0,4 м/сек и стало прорезаться опорами со скоростью 0,01-0,02 м/сек. Толщина льда у опор составляла 45-60 см. Пройдя 50 м, поле остановилось, нанеся существенные повреждения: железобетонные ростверки оказались смещенными (до 8 м), некоторые повернуты, почти все металлические сваи изогнуты, другие сломаны Давление льда на отдельную опору оценено авторами в 270 т. И.Н. Шафир и Р.И. Гинсберг (1, 10] сообщают случай повреждения морских гидротехнических сооружений в одном из северных портов СССР. Ледяное поле шириной около 10 км, толщиной 0,6 м 6 мая 1941 г. было занесено течением и приливом на ряжевый пирс; 15 ряжей оказались сдвинутыми (некоторые до 8 м) и повреждены. По усилию, необходимому для сдвига ряжа, сила удара оценена авторами в 100 т, что эквивалентно контактным напряжениям 23,8 т/м2. А.М. Рябухо [1, 11] привел случай повреждения массивной опоры (сдвиг части опоры моста) на одной крупной реке Китая. Авария была вызвана воздействием принесенного ветром крупного ледяного поля толщиной 0,4 м в декабре 1955 г. при температуре воздуха -20°С. Величина давления оценена в 300 т, что эквивалентно 120 т/м2. Если учесть, что авария была в декабре при морозе -20°С, то такое давление не может считаться чрезмерным. Скорость дрейфа ледяного ноля под воздействием ветра на основании исследований В.В. Шулейкина [12] и П.А. Кузнецова [13] может быть для различных условий принята по формуле Vл = 0,02W, где Vл - скорость дрейфа, м/сек; W - расчетная скорость ветра, м/сек; 0,02 - «ветровой» коэффициент. Анализ этого вопроса [1, 13] .показывает, что расчетная скорость ветра, действующая на всю площадь ледяного поля, должна быть меньше максимальной скорости отдельных «струй» ветра. Чем больше площадь льдин, тем меньше должна быть расчетная скорость ветра. Для предварительного решения можно пользоваться рекомендациями П.А. Кузнецова [13], предложившего данные:
Так как площадь дрейфующих ледяных полей на водоемах Сибири редко превышает 100 тыс. м2, то скорость их движения может достигать значения Vл = 0,02·31 = 0,62 м/сек, а для больших льдин может быть и большей. Небольшие льдины обладают меньшим запасом кинетической энергии и обычно не представляют опасности для мостовых опор. Рекомендуемые приемы оценки ледовых нагрузок С учетом особенностей ледотермического режима водохранилищ в условиях Сибири можно рекомендовать следующие приемы определения расчетных ледовых нагрузок на опоры мостов, работающие в условиях водохранилищ. А. Возможные расчетные схемы: 1) крупное ледяное поле площадью Ω, толщиной h весной движется со скоростью vл к опоре и после удара прорезается опорой; 2) после контакта с опорой это поле останавливается, опора не врезается в льдину на полную ширину; 3) ледяное поле, стоящее у опоры, оказывает на нее статическое давление под влиянием ветра на верхнюю поверхность льдины. Б. Расчетные приемы: для первой расчетной схемы следует пользоваться зависимостью, рекомендованной СН 200-62 и СН 76-59,
для второй схемы можно рекомендовать формулу
обоснованную и внесенную в проект новых ТУ на ледовые нагрузки [15]; для третьей схемы следует использовать формулы (20) и (18) нормы СН 76-59
В. Расчетное давление За расчетное давление следует принять наименьшее из подсчитанных по формулам (1) и (2). Если H2 < H1 то льдина остановится у опоры, оказывая давление H2; прорезание льдины опорой будет отсутствовать. Если H1 < H2, то льдина будет прорезаться опорой при максимальном давлении Н1. Давление, определяемое по формуле (3), невелико и не может быть расчетным. Г. Расчетные параметры: m - коэффициент формы опоры, принимаемый по табл. I СН 76-59 или СН 200-62; Rp - расчетный предел прочности льда при раздроблении (с учетом местного смятия) на основании СН 76-59 и наблюдений на Новосибирском водохранилище, принимаемый равным к периоду подвижки 75 т/м2; высокого ледохода - 45 т/м2. Учитывая, что дрейф ледяных полей возможен лишь при больших разводьях (когда существенная часть ледяного покрова растает или раздробится), можно не вводить увеличение прочности для высоких горизонтов вдвое, предусмотренное СН 76-59 и СН 200-62 для северных районов СССР; В - ширина опоры на уровне ледохода, м; h - расчетная толщина льда, принимаемая на основании наблюдений на Новосибирском и Братском водохранилищах равной 0,7 наибольшей за зимний период толщины 1 % обеспеченности, м; V1 - скорость движения льдины (не более 0,6 м/сек) под влиянием ветра, определяемая по зависимости
W - расчетная скорость ветра, принимаемая по П. А. Кузнецову в зависимости от площади ледяного поля (см. выше). При этом необходим детальный учет геоморфологических особенностей мостового перехода и наблюденных скоростей ветра для заданного района. Несомненно, что при узких «заливах» водохранилища, окруженных горами, т. е. при своеобразных каньонах, расчетную скорость ветра можно снизить в отдельных случаях даже вдвое, но этот вопрос должен решаться конкретно для заданных местных условий. Следует учитывать вероятное направление ветра в период возможного дрейфа, конфигурацию берегов в плане залива, высоту берегов и результат натурных наблюдений в створе мостового перехода; Ω - расчетная площадь ледяного поля, определяемая по местным условиям. При отсутствии данных можно принимать льдины примерно квадратными со стороной, равной пролету моста. В естественных условиях на реках Сибири размеры наиболее часто встречающихся крупных льдин в период ледохода составляют 1/8-1/20 ширины реки; α - угол заострения опоры в плане. Полуциркульные опоры можно принимать при расчете за треугольные с углом заострения 2α = 140°. Для снижения величины расчетных усилий, если они определяются формулой (2), целесообразно принимать на уровне ледохода заостренное очертание опор в плане. ЗАКЛЮЧЕНИЕ Внесенные предложения носят предварительный, ориентировочный характер. Поэтому крайне желательны систематические наблюдения за ледовыми условиями на вновь создаваемых водохранилищах, которые позволят уточнить предложенные рекомендации по выбору расчетных размеров льдин и пределов прочности льда. Необходима также постановка наблюдений за величиной фактического давления льда на опоры мостов. Проще всего для этого использовать разработанный в НИИЖТе кинематический способ, использованный уже более чем в 40 случаях. Фиксируя изменение скорости движения ледяного поля (при помощи киноаппарата или специальной аппаратуры), после его встречи с опорой моста возможно определить и силы взаимодействия, возникающие между сооружением и ледяным покровом. Использование этого метода, подробно описанного в литературе [1; 15, 16, 17 и др.], позволит уточнить предлагаемые приемы и обеспечить надежность возводимых сооружений без лишних запасов прочности. ЛИТЕРАТУРА 1. Коржавин К.Н. Воздействие льда на инженерные сооружения. Новосибирск, Изд-во СО АН СССР, 1962. 8. Бутягин И. П. Прочность ледяного покрова в ледовых нагрузках на сооружение. Труды ТЭИ СО АН СССР, вып. 11, Новосибирск, 1961. 10. Шафир И.Н., Гисберг Р.И. Аварии морских гидротехнических сооружений, М, 1942. 12. Шулейкин В.В. Физика моря. М., 1941. 13. Кузнецов П.А. Действие льда на сооружения морских портов и защита от него. Л., 1939. 14. Госстрой СССР. Технические условия на ледовые нагрузки на речные сооружения. СН 76-59. М., 1960. Канд. техн. наук В.М. САМОЧКИНОСОБЕННОСТИ ОБРАЗОВАНИЯ ЗАТОРОВ И ЗАЖОРОВ НА РЕКАХ СИБИРИЗимний режим рек Сибири имеет ряд особенностей, которые обусловливаются климатическими, гидрологическими, морфологическими и другими факторами. Наиболее ярко особенности ледового режима рек проявляются в периоды замерзания и вскрытия водотоков. В эти периоды в результате заторных и зажорных явлений на реках возможны высокие подъемы уровня воды и затопления больших территорий, разрушение льдом различных гидротехнических сооружений и опор мостов. Поэтому при проектировании мостовых переходов, плотин, водозаборов, береговых креплений и других сооружений следует учитывать возможность образования заторов и зажоров на реках, а изучение этих явлений - важная проблема в практическом и теоретическом отношении. К настоящему времени накоплен большой материал по зимнему режиму рек и, в частности, по изучению заторных и зажорных явлений. В работе В.Я. Альтберга [1] рассмотрены основные вопросы внутриводного ледообразования; вопросы гидротермики речных потоков детально разобраны в работах Б.В. Проскурякова [43], С.Н. Крицкого, М.Ф. Менкеля и К.И. Россинского [27], B.В. Пиотровича [41], а из зарубежных авторов следует упомянуть цепную работу О. Девика [21] и др. Анализ повеления внутриводного льда в потоке проведен В.М. Маккавеевым [34], C.Я. Вартазаровым [15], Д.Н. Бибиковым [6]. Большой материал накоплен по исследованиям шуголедового режима рек и борьбы с шуголедовыми затруднениями на гидроузлах [7, 13, 14, 18, 20, 22, 24, 25, 38, 40, 42, 44, 51]. Заторные явления на реках изучались Н. М. Максимовичем [35], Е.В. Близняком [8, 9], Ф.И. Быдиным [12], Б.А. Аполловым [3], Л.Г. Шуляковским [50, 51] и др. Большие исследовательские работы по изучению физико-механических свойств речного льда и воздействия его на сооружения выполнены К.Н. Коржавиным [26] и И.П. Бутягиным [10]. Заторы льда на реках Сибири изучались И.И. Волковым [17], И.Я. Лисером [30, 31], Я.И. Марусенко [36]. Опубликованы исследования по замерзанию и вскрытию рек в естественных и зарегулированных условиях [11, 45, 46].
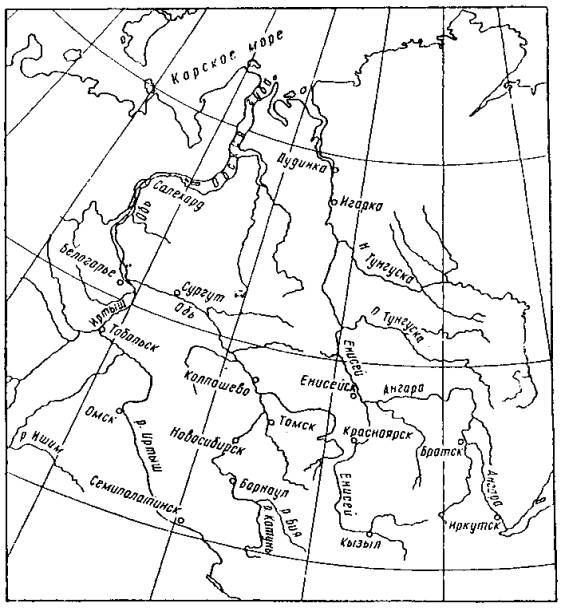
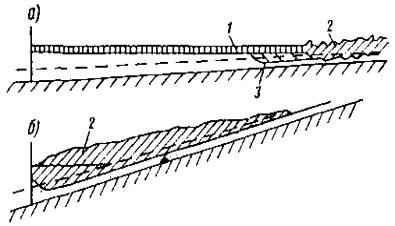
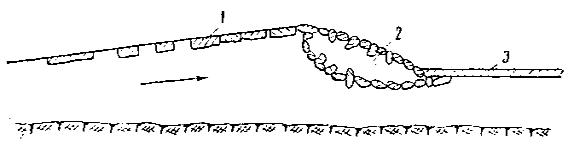
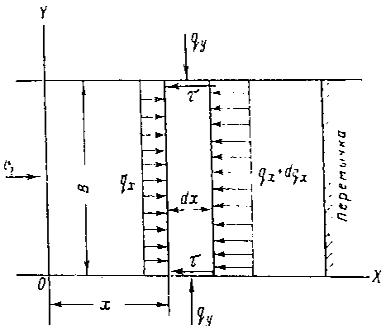
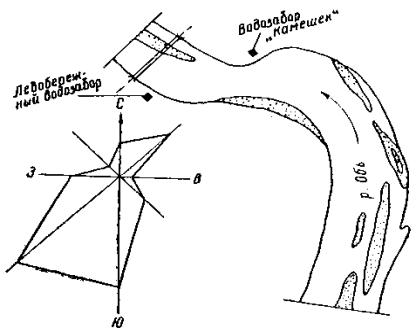
Рис. 1. Гидрографическая схема Оби и Енисея Ледовый режим рек Сибири отличается большим разнообразием, рассмотрим его применительно к таким рекам, как Ангара, Енисей и Обь. Ангара, Енисей и Обь - крупнейшие реки не только Советского Союза, но и мира, отличаются как многоводностью, так и своей длиной. Они имеют преобладающее общее направление течения с юга на север, пересекая ряд физико-географических зон (рис. 1). Верховья этих рек имеют значительные уклоны водной поверхности, постепенно уменьшающиеся к устью. Для территории, по которой протекают рассматриваемые реки, характерны суровая и продолжительная зима, способствующая образованию мощного ледяного покрова на реках, и короткие переходные периоды осени и весны. Осеннее похолодание наступает интенсивно с редкими случаями возврата тепла. Поэтому продолжительность осеннего ледохода на большинстве рек Сибири небольшая. Благодаря дружной весне вскрытие рек происходит при высоких подъемах уровня воды и еще сохранившемся толстом и прочном ледяном покрове. Это обстоятельство, а также общее направление течения рек с юга на север способствует образованию весенних заторов льда на реках. Общие закономерности образования зажоров Зажором называется скопление масс шуги с включением битого льда, снежуры и пр., создающее в осенне-зимний период стеснение русла реки на отдельном ее участке и вызывающее выше этого участка местное повышение уровня воды. Как правило, зажоры образуются на шугоносных реках в период формирования ледяного покрова, а также при ледоставе ниже полыней, являющихся очагами образования шуги. Шуголедовые процессы на реках представляют собой явления, зависящие от очень большого количества факторов. Учитывая, что в осенний период в Сибири происходит устойчивое нарастание отрицательных температур воздуха, шуголедовые явления рассмотрим в зависимости от продольного профиля водотока и скорости течения, от морфологических особенностей участка русла, от влияния водоподъемных плотин и др. Характер ледообразования на реках в сильной степени определяется скоростью течения. В потоках с незначительными скоростями (v ≤ 0,5 м/сек) и, следовательно, со слабым турбулентным перемешиванием, переохлаждение воды под влиянием отрицательных температур воздуха происходит в поверхностных слоях реки. Здесь и образуются кристаллы льда, быстро смерзающиеся в ледяные поля. Одновременно растут забереги. Ледяной покров устанавливается спокойно без образования практически значительных количеств шуги. При скорости течения более 0,5 м/сек вследствие интенсивного перемешивания и резкого увеличения теплопроводности водных масс переохлажденной оказывается не только поверхностная пленка воды, но и вся толща речного потока. Выделение кристаллов льда становится возможным в любой точке живого сечения реки, в том числе и у дна (донный лея). Всплывшие на поверхность реки массы внутриводного и донного льда образуют шугу. В состав шуги входят также комья снега и ледяная корка, возникающая на поверхности шуговых ковров. Скорости течения воды оказывают существенное влияние на характер транспортирования шуги потоком. Из наблюдений известно, что шуга в форме поверхностных ковров разной густоты и мощности наблюдается при скоростях, не превышающих 1,5 м/сек. При больших скоростях поверхностные ковры шуги разрушаются поперечными турбулентными токами, а кристаллы льда захватываются в толщину потока. Если скорость течения превышает 2 м/сек, то захват шуголедовых элементов потоком оказывается настолько интенсивным, что скорость в 2-2,5 м/сек обеспечивает обнажение поверхности потока даже при устойчивых отрицательных температурах воздуха. В зависимости от величины скорости течения шуголедовые образования при возникновении преграды их движению могут оставаться у поверхности потока или подныривать под кромку. А.С. Образовский [39] на основании опытов А.М. Латышенкова [29] определил скорости потока, при которых начинается подныривание льда под кромку (табл. 1). Таблица 1
В результате анализа условий образования шуголедовых образований А.С. Образовский намечает четыре характерные скорости течения, которые играют важную роль в шуголедовом режиме. Первая скорость vк1 = 0,5 м/сек устанавливает нижний предел шугоносности потоков. При скорости течения v < vк1, ледяной покров на реке обычно устанавливается без шуголедовых осложнений. На больших реках при сильном ветре шуголедовые образования возможны. Скорость vк1 одновременно является и некоторой характеристикой движения шуголедовых ковров. Если скорость течения в реке уменьшается до значений vк1, в условиях мороза шуголедовые ковры быстро смерзаются и образуется ледяной покров. Вторая скорость vк2 устанавливает предел, внутри которого шуговые ковры не будут подныривать под кромку ледостава. Величина этой скорости (в м/сек) в первом приближении равна vк2 = 0,7 + 0,067Н, где Н - глубина потока, м. Третья скорость vк3 устанавливает предел, за границами которого шуголедовый материал транспортируется в значительной части в толще потока в виде шуголедяной взвеси. По опытным данным величина vк3 = 1,5 м/сек. С.Я. Вартазаров [15] утверждает, что при скорости v ≥ 1,5 м/сек поток способен транспортировать шуголедовый материал даже под телом шуго-зажора. Четвертая скорость vк4 устанавливает предел, при достижении которого поверхность потока окажется полностью обнаженной. Величины третьей и четвертой скоростей зависят от концентрации шуги в потоке. Д.Н. Бибиков [6] отождествил шуголедяной покров с пульпой и определил критическую скорость, обеспечивающую полное взвешивание шуголедового материала по формуле В.С. Кнороза. В.М. Потапов [42] на основании рассмотрения энергетического состояния шуголедового потока также предложил формулу для определения критической скорости, при которой шуга распределяется по живому сечению. Анализируя эти формулы, А.С. Образовский [39] нашел в них ряд неточностей и в результате теоретических проработок рекомендует следующую зависимость для определения vк3:
где С - коэффициент Шези; μ - корректирующий коэффициент, рекомендуемый предварительно принимать равным 0,5-0,7; hш - толщина слоя шуги при v < vк3, м; р - пористость шуги. Образование зажоров на реках происходит в процессе формирования ледостава, на что оказывают существенное влияние характер продольного уклона и морфологические особенности русла. Рассмотрим наиболее типичные случаи формирования ледостава и зажоров, следуя при этом обобщениям, которые сделал А.С. Образовский. Реки равнинного типа с плавным профилем призматическим руслом (скорость течения vк1 < v < vк2). На реках этого типа ледяной покров устанавливается путем задержания плывущей шуги у кромки. Движение шуги в период ледохода наблюдается только по поверхности потока, вследствие чего теплоотдача с водной поверхности существенно ограничивается, ровно как и образование внутриводного льда. Вспышки интенсивного образования последнего связаны со случаями полного обнажения поверхности водотока. Существенных зажоров на реках этого типа не образуется. Реки предгорной зоны с плавным профилем и призматическим руслом (скорость течения vк2 < v < vк3). Кромка ледостава на реках этого типа формируется более сложным путем. На некотором протяжении (рис. 2) кромка заторошивается, сечение реки под ней сильно забивается подныривающими под кромку шуговыми коврами, перед кромкой создается подпор, который приводит к уменьшению скоростей и прекращению подныривания. Кромка ледостава начинает развиваться вверх по течению. В области выклинивания создавшегося подпора снова начинается подныривание ковров под кромку. Образование ледостава сопровождается некоторым подъемом уровней ∆Н и образованием зажоров.
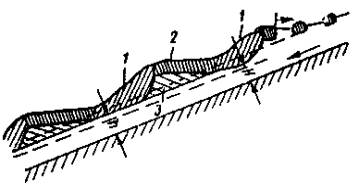
Рис. 2. Схема формирования ледяного покрова при скоростях течения vк2 < v < vк3: 1 - заторошенный участок ледостава, развивающийся при подныривании ковров под кромку; 2 - участок ледостава, формирующийся без подныривания ковров под кромку; 3 - отложение шуги под ледяным покровом В первом приближении А.С. Образовский рекомендует ∆Н определять по формуле ∆Н = 0,33φН + δ и h = 1,33φН, где Н - глубина .потока в открытом русле, м; h - глубина воды под ковром шуги, м; δ - глубина погружения шуги, м; φ – I : Iш; I - продольный уклон реки. Горные реки при скорости v > vк3. Формирование ледостава может происходить, как и в предыдущем случае, однако под шуголедяным покровом в той или иной мере будет транзит шуги. На вышележащем участке при скорости v > vк4 ледостав вообще не возникает. Вследствие этого вышележащий участок реки будет продуцировать внутриводный лед в течение всего зимнего периода. Вся масса этого шугольда будет поступать под ледяной покров участка со скоростями v < vк4. Шугозажорные явления будут развиваться в очень сложных формах, в некоторых случаях обусловливающих блуждание потока и потерю части его стока на наледные образования. Слабоизвилистые реки равнинного типа со ступенчатым профилем. Основным морфологическим элементом русла для этих рек является комплекс «перекат-плес». Скорости течения обычно изменяются в пределах: на плесах vк1 < v < vк2, на перекатах vк2 < v < vк3. В связи с этим шуголедовые процессы протекают по схеме, приведенной на рис. 3, а. Надвигающаяся снизу кромка ледостава вызывает некоторое повышение уровня ∆Н. Плес замерзает за счет остановившихся шуголедяных ковров. При подходе кромки к сечению, в котором начинается процесс подныривания под кромку, возникает зажор. Последний, вызывая подпор на перекате и прекращая подныривание, дает возможность кромке ледостава двигаться вверх по течению через перекат на вышележащий плес.
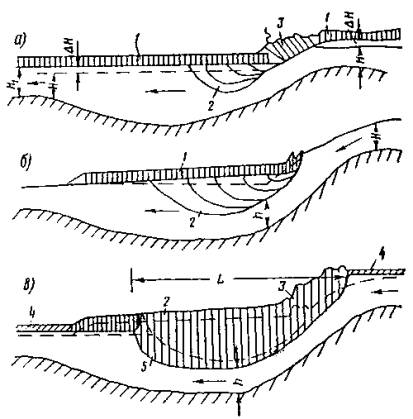
Рис. 3. Схема формирования ледостава на участке «плес-перекат»: а - при низких перекатах; б - при высоких перекатах с образованием полыньи, в - то же с перекрытием полыньи; 1 - часть ледяного покрова, формирующаяся без подныривания ковров шуги; 2 - отложения шуги под ледяным покровом; 3 - заторошенная часть ледяного покрова; 4 - ледяной покров на полынье; 5 - последующие отложения шуги в шугозажоре При высоких перекатах и малых скоростях в плесах кромка ледостава может возникнуть на плесе за счет смерзания шуговых ковров, а на перекате некоторое время может сохраниться полынья, в которой будет идти образование шуги. В этом случае ниже переката может получить значительное развитие зажор (рис. 3, б). Процесс перекрытия переката сохранится прежним: должен возникнуть подпор в результате развития зажора в верхней части плеса, после чего скорости на перекате уменьшатся и полынья покроется льдом (рис. 3, в). Порожистые реки со ступенчатым профилем. Развитие шуголедовых явлений на реках этого типа протекает аналогично предыдущему с тем отличием, что эти процессы развертываются в течение всей или большей части зимнего периода. В формировании зажора участвует значительное количество шуголедяного материала. Под тело зажора, формирующегося ниже порогов, шуговидная смесь поступает в сильно переохлажденном виде, поэтому процессы примерзания шуги к нижней поверхности зажора развиты более интенсивно. Скорости, обеспечивающие шуготранзит под тело или в теле шугозажора, потребуются соответственно большими 1,5 м/сек. Завлечение шуги в глубину в пределах формирующихся зажоров может быть очень значительным. Так, Ф.И. Быдин [12] отметил случай отложения шуги под ледяным покровом на глубине 18 м, а X. Барнес даже на глубине 27 м. Замечено, что зажоры ниже порогов подвержены непрерывному переформированию.
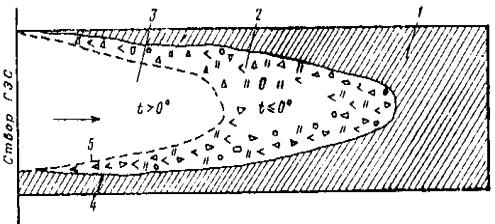
Рис. 4. Схема шугозаполнения русла: а - на излучине русла; б - в обходной протоке; 1 - место завязки очага шугозажора; 2 - контур заберегов; 3 - направление обходных проток; 4 - основное русло; 5 - рукав; 6 - заберег при входе в рукав Пороги в продолжение зимы могут оставаться открытыми и поставлять шугу в зажор в течение всего ледоставного периода. Участки рек с крутыми поворотами и разветвлениями русла. Крутые излучины часто являются местом формирования головы зажоров (рис. 4, а). Движущаяся шуга плотным слоем идет вдоль вогнутого берега, оставляя свободной часть поверхности у выпуклого берега, где образуются забереги, которые смыкаются с движущимся полем шуги, после чего начинается отложение шуги под заберегом. Если выпуклый берег как обычно невысок, то подпертая вода устремляется в обход плеса, вызывая иногда образование небольших проток. Это в свою очередь приводит к усилению формирования головной части шугозажора, который постепенно развивается вверх. Сложная ситуация складывается и на участках разветвленного русла (рис. 4, б). Если эта система симметрична, то на верховой стрелке острова обычно наблюдаются торосистые навалы шуги, а у корней верховых побочней формируются забереги. Небольшая разница в высоте перекатов или разница в густоте подходящих сверху ковров шуги у каждого из берегов приводит к тому, что один из перекатов, обычно с более высоким гребнем, полностью закрывается зажором. Точно прогнозировать возможную шуголедовую ситуацию очень трудно. В каждом отдельном случае необходим соответствующий комплекс наблюдений для выявления закономерностей замерзания реки. В годы с неустойчивым похолоданием сложность шуголедовых процессов, происходящих на реках, увеличивается (удлиняется период внутриводного ледообразования, подвижки зажоров, образование вторичных зажоров и др.). Верхние бьефы плотин. В верхних бьефах плотин на равнинных реках скорости течения воды незначительны. В тихую морозную погоду водохранилище замерзает, дружно покрываясь кристаллическим ледяным покровом. Если в период ледообразования наблюдается сильный ветер и массы воды перемешиваются ветровой волной, тогда в толще воды идет образование внутриводного льда, а на поверхности - шуговых ковров. После образования ледяного покрова большие скопления шуги отмечаются у наветренных берегов. Зажоры в подпертых бьефах образуются в зоне выклинивания подпора и выше (рис. 5, а). Шуготранзита по водоему обычно не наблюдается. Подпоры в руслах перед зажорами могут достигать 4-6 м. Интенсивность шуголедовых явлений в зоне выклинивания подпора зависит от особенностей водотока.
Рис. 5. Схема формирования ледяного покрова в верхнем бьефе: a - на равнинных реках; б - на горных реках; 1 - ледяной покров, формирующийся без подныривания льда; 2 - тело шугозажора; 3 - отложения шуги под ледяным покровом В малых по объему водохранилищах, устраиваемых на водотоках горного типа, зажорными массами льда заполняется вся емкость (рис. 5, б). Под зажорами создается течение, обеспечивающее перенос шуги через весь бьеф [13, 14, 16]. Зажоры на реках Сибири Река Ангара. Зимний режим Ангары по сравнению с другими реками Сибири изучен хорошо. Значительный вклад в изучение ледотермического режима реки внесли специалисты Гидроэнергопроекта, опубликовавшие в 1964 г. книгу «Ледотермика Ангары» [20]. Река Ангара - правый приток Енисея - вытекает из озера Байкал и впадает в Енисей в 83 км выше г. Енисейска. Длина реки 1826 км, полное падение уровня 378 м. Ангару принято делить на следующие три участка: верхний - от истока до устья р. Оки длиной 664 км, падение на этом участке 141,5 м; средний, или порожистый, участок - от устья р. Оки до впадения р. Илима, длина участка 280 км, падение 89,5 м; нижний участок - от устья р. Илима до устья р. Ангары, протяженность 882 км, падение 144 м. Ангара питается в основном за счет вод озера Байкал. Поэтому в отличие от других рек Сибири Ангара в зимний период имеет повышенную водность (табл. 2). Расходы воды в осенне-зимний период отличаются равномерностью и значительной величиной. Характерная особенность гидравлического режима - чередование отдельных порожистых участков с большими скоростями течения. Если средний уклон Ангары равен 0,000206, то на порожистых участках ее они изменяются примерно от 0,001 до 0,006 (табл. 3). Помимо отмеченных наиболее характерных участков, имеется много шивер и перекатов с большими падениями, уклонами, скоростями. Данные наблюдений гидрометрических станций указывают на то, что скорости течения и не на порожистых участках реки значительны. При открытом русле средние скорости течения в верхнем течении реки 1,5-2 м/сек, в среднем течении 1,2-1,6 м/сек и в нижнем 0,9-2 м/сек. Такие скорости превышают вторую (vк2 ) и третью (vк3) критические скорости. На перекатах и шиверах скорости течения значительно превышают vк3, обеспечивая транспорт шуги в толще потока в виде шуговой взвеси. В соответствии со скоростями течения и особенностями продольного профиля развитие шуголедовых явлений на реке происходит по ранее описанным типам. Рассмотрим кратко особенности процесса ледообразования и установления ледостава. Таблица 2
Таблица 3
Вследствие того, что из озера Байкал в Ангару в течение всей зимы поступает относительная теплая вода, несмотря на одновременность наступления похолодания по всей длине реки, ледообразовательные процессы раньше всего наступают в низовьях реки. В дальнейшем по мере охлаждения воды они распространяются вверх со значительным отставанием по сравнению с остальными реками района и датами установления морозов. Вода в Ангаре благодаря большой турбулентности потока переохлаждается и в ней происходит обильное образование внутриводного льда в виде дискообразных или крупчатых кристаллов диаметром 1-2 мм. Внутриводный лед образуется и на дне потока в виде губчатых масс. Всплывший на поверхность реки донный лед, скопления внутриводного льда у поверхности и снежура образуют шугу, которая составляет основную массу льда в осенне-зимнем ледоходе (рис. 6).
Рис. 6. Шугоход на Ангаре Вследствие ступенчатого профиля реки шуга и лед в процессе транспортирования претерпевают значительные изменения. На плесовых участках отдельные скопления шуги и льдины смерзаются между собой в ледяные поля. Проходя через пороги и шиверы, ледяные поля снова распадаются па отдельные льдины. Продолжительность шугохода на Ангаре зависит от времени прохождения через тот или иной створ нулевой изотермы и кромки льда, от длины ледообразующего участка, а также от образования выше по течению зажоров и заторов льда, дающих новое начало кромки ледяного покрова. Продолжительный ледоход наблюдается в верхнем течении Ангары (табл. 4). Здесь длина ледообразующего участка настолько мала, что льда не хватает на формирование ледяного покрова и шугоход принимает затяжной характер. Толщина плывущего слоя шуги изменяется в больших пределах: па верхнем участке реки не превышает 1 м, в среднем и нижнем течении может достигать 2 м. Таблица 4
При решении задачи о давлении шуговых полей на сооружение необходимо учитывать скорость движения и размеры плывущих скоплений льда и шуги (табл. 5). Таблица 5
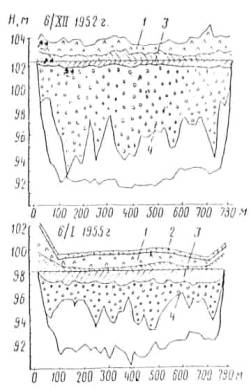
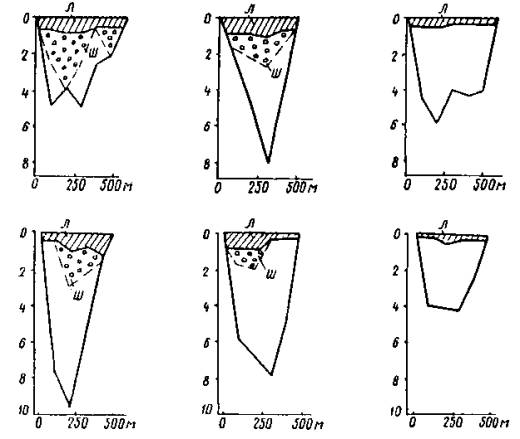
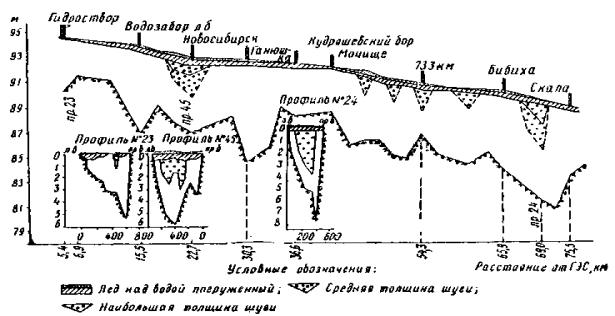
Образование зажоров связано с особенностями установления ледостава на реке. Процесс образования ледяного покрова сильно растянут по времени. Вначале ледяной покров устанавливается в низовьях Ангары на мелководных перекатах и шиверах (середина ноября), в среднем течении - в конце ноября, а в верхнем - в конце декабря. Установление ледостава сопровождается образованием зажоров, чему способствуют своеобразный продольный профиль реки и большие скорости течения. На всем .протяжении Ангары в зимний период образуется каскад зажоров различной мощности. Особенно мощные зажоры располагаются в местах резкого перелома продольного профиля реки ниже порога. Поэтому особенно много зажоров образуется на среднем участке. Здесь, например, от г. Братска до с. Невон на реке образуется 14 крупных зажоров. В табл. 6 приведены сведения по некоторым зажорам на Ангаре, а на рис. 7 и 8 - характерные разрезы по ним. Из таблицы следует, что толщина слоя шуги в зажоре может достигать 7-8 м, а подъем уровня воды 5-9 м. Таблица 6
Формирование зажоров на Ангаре происходит продолжительное время и сопровождается подвижками льда в зажоре, что может привести к почти полной забивке русла и катастрофическим последствиям. Катастрофические размеры зажор принимает тогда, когда окончание его формирования совпадает с резким потеплением [20]. В этом случае еще не окрепший шуголедяной покров смещается вниз и почти полностью закупоривает живое сечение реки шугой и льдом. Примером может служить зажор в 1952-1953 г.г., вызывавший затопление прибрежной части Иркутска. Иногда при формировании зажоров происходит 10-12 крупных подвижек льда, а скорость движения льда в это время составляет примерно 0,3 м/сек. Объем поверхностного льда и шуги в зажорах достигают существенных значений. Так, например, на наиболее исследованном Боковском зажоре объем поверхностного льда составляет 705 ´ 103 ÷ 3209 ´ 103 м3, объем шуги – 4020 ´ 103 ÷ 11240 ´ 103 ´ 10 м3. Зажоры обмерялись сразу же после ледостава. В наиболее мощном Падунском зажоре количество шуги достигало 23925 ´ 103 м3 (3/I 1956 г.). К концу зимы количество шуги в зажорах уменьшается в несколько раз, тогда как общее количество льда в зажоре остается почти без изменений. Это обстоятельство объясняется интенсивным нарастанием ледяного покрова на зажорных участках реки. Строительство гидростанций нарушает естественный режим водотоков. Так, в условиях работы Иркутской ГЭС шугообразование происходит на более коротком участке, ограниченном в верхней части профилем нулевых температур и плотиной ГЭС. Следовательно, снизилось количество ледяного материала, поступающего в кромке льда, что привело к более продолжительному периоду образования зажоров в нижнем бьефе. Объем ледовой массы в зажоре тоже снизился, подъем зажорных уровней остался близким к бытовым величинам. Однако эти данные предварительные и вопрос влияния регулирования стока на ледотермический режим рек еще не изучен. Река Енисей. Одна из самых многоводных рек мира Енисей начинает свой путь в центре Азии, а заканчивает на Крайнем Севере у Карского моря. По гидрологическим и морфологическим признакам выделяют три участка: верхний от слияния рек Ка-Хема и Бий-Хема до устья р. Тубы - 625 км; средний от устья Тубы до устья Ангары - 725 км; нижний от устья Ангары до впадения в Карское море - 2130 км. Первые ледовые образования появляются в низовьях реки в середине октября, на среднем и верхнем Енисее - в конце октября. Ледостав устанавливается в таком же порядке: сначала в нижнем течении реки - в конце октября, затем на среднем и верхнем течениях - 15-20 ноября (табл. 7). Таблица 7
Река замерзает при пониженной водности. На сентябрь-октябрь приходится примерно 17-20 %, на ноябрь-март 8-12 %, а на лето (июнь-июль-август) падает 45-60 % годового стока Енисея. Расходы воды и скорости течения перед замерзанием реки в 1960 г. приведены в табл. 8, из которой следует, что абсолютные значения расхода воды в среднем и нижнем течении реки велики, скорости же течения уступают ангарским. Таблица 8
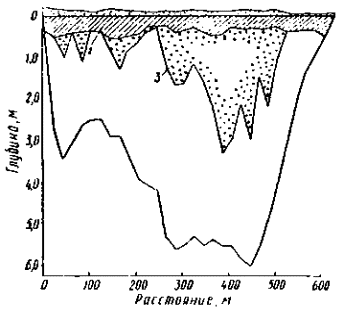
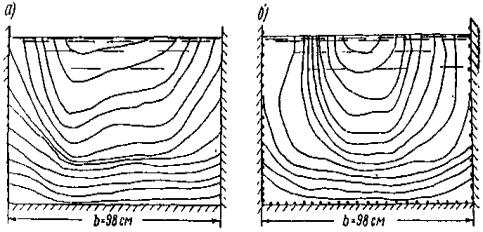
По характеру течения Енисей можно отнести к описанному выше типу - слабоизвилистые реки равнинного типа со ступенчатым профилем. Скорости течения на плесах изменяются в пределах vк1 < v < vк2, на перекатах vк2 < v < vк3. Шуголедовые процессы протекают примерно, как изображено на схеме рис. 3, а, за исключением устьевого участка реки, где скорости течения небольшие и река замерзает как слабопроточное водохранилище. В нижнем течении реки ледоход формируется за счет льда поверхностного образовании, в среднем и верхнем наблюдается интенсивное образование внутриводного льда (шуги), особенно на порожистых участках. Здесь в процессе ледохода участвует и шуга, и лед поверхностного образования. Значительное количество шуги в Енисей поступает из горных и порожистых рек: Абакана, Маны, Ангары, Подкаменной и Нижней Тунгуски и др. В устье Енисея ледяной покров образуется почти без ледохода. Отсюда кромка ледостава распространяется вверх по реке со скоростью 30-50 км в сутки и за 6 суток достигает Туруханска [5], от Туруханска выше по течению кромки ледостава передвигаются со скоростью 40 км в сутки и через 15 суток подходит к месту впадения Подкаменной Тунгуски. Одновременно на Енисее образуются новые очаги ледостава: ниже Осиновского порога в среднем 8 ноября, у д. Атаманово, в 70 км ниже Красноярска, 10 ноября, вблизи Минусинска 15 ноября. Ледяные перемычки на Енисее, как отмечает Н.П. Бахтин [5], образуются в местах резкого снижения скорости потока на глубоких, но суженных участках реки, где накапливается шуга и лед и при сильных морозах быстро смерзается. Ниже ледяных перемычек долго сохраняются полыньи. С начала ледостава уровень воды в реке быстро повышается вследствие влияния подпора, образующегося в результате появления ледяного покрова и зажоров. Величина шуголедяных зажоров и осенних заторов на Енисее меньше, чем на Ангаре. Повышение уровня составляет: у Кызыла - 2-3 м, Означенного и Красноярска 1,5-2 м и только ниже впадения Ангары подъем уровня довольно высок и составляет у Енисейска 4-5 м. Ниже Игарки образование ледостава часто наблюдается без ледохода, здесь не образуется зажоров, поэтому значительных повышений уровня не происходит. В случае осенних подвижек льда живое сечение реки иногда значительно забивается шугой и битым льдом, вследствие чего образуются мощные зажоры. Подобный случай описан И.Я. Лисером [32]. Осенью 1957 г. ледостав на Енисее в. районе Красноярска наступил 18/XI при весьма высокой отметке уровня воды. Подъем уровня при ледоставе составил 2,2 м, что на 0,9 м выше нормального. В течение ночи с 18 на 19/XI уровень повысился еще на 56 см. В это время наступило потепление до 0,2°С. В связи с потеплением и высоким уровнем воды при установлении ледостава во второй половине дня 19/XI на Енисее у Красноярска произошла подвижка льда. Подвижка продолжалась около 4 ч и распространилась на участок реки длиной примерно 25 км. Уровень воды при подвижке изменялся незначительно. Лед при подвижке в районе Красноярска перемещался довольно быстро сплошной массой без заметного разлома смерзшегося ледяного покрова на части. Двигался он лишь по центральной части реки. Однако не везде движение льда при подвижке проходило спокойно. В ряде мест ледостав после подвижки устанавливался бурно со значительными нагромождениями льда и взломом заберегов. Маршрутная ледомерная съемка (рис. 9) на участке выше и ниже Красноярска, проведенная Ленгидэпом сразу же после установления ледостава, указывает на значительное уплотнение ледовых масс в возникшем зажоре. Подледная шуга отмечена в большинстве мест (на 17 профилях из 23), но лишь на двух профилях шуга была по всей ширине реки. Наибольшая глубина слоя шуги достигала 3 м, а максимальное стеснение живого сечения русла свыше половины. Средняя глубина слоя шуги подо льдом на всех 27 профилях оказалась равной 0,4 м.
Рис. 9. Поперечные профили русла Енисея: л - кристаллический лед; ш - шуга Река Обь. Эта река, как и Енисей, берет начало на юге Сибири, в горах, и заканчивает свое течение на Крайнем Севере, впадая в Карское море. Длина Оби от слияния рек Бии и Катуни до устья 3680 км, средний уклон около 0,000042. От слияния рек Бии и Катуни до устья р. Томи - уклоны 0,00011-0,000076, от устья Томи до устья Иртыша - 0,000076-0,000023, от устья Иртыша до впадения в Обскую губу - 0,000016. Обь характеризуется плавным продольным профилем, значительной извилистостью и разветвленностью русла. Водность Оби и скорости течения перед замерзанием можно характеризовать данными, сведенными в табл. 9 и 10. Таблица 9
Замерзание реки происходит при пониженной водности и скоростях течения, обычно не превышающих 1 м/сек. Следовательно, формирование ледостава в соответствии с отмеченными гидрологическими особенностями реки происходит по рассмотренным ранее типам, как для реки равнинного типа с плавным профилем и рек с крутыми поворотами и разветвленными руслами при скоростях течения vк1 < v < vк2. Таблица 10
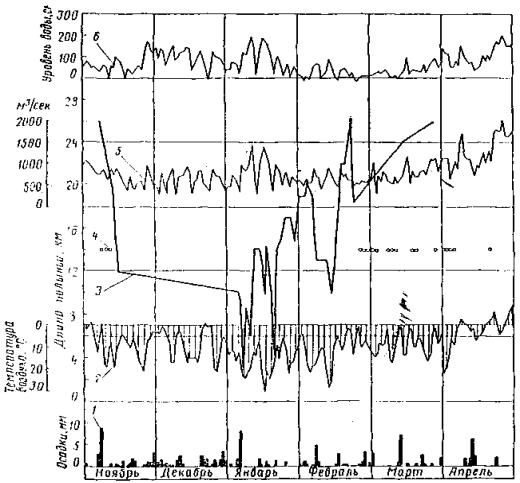
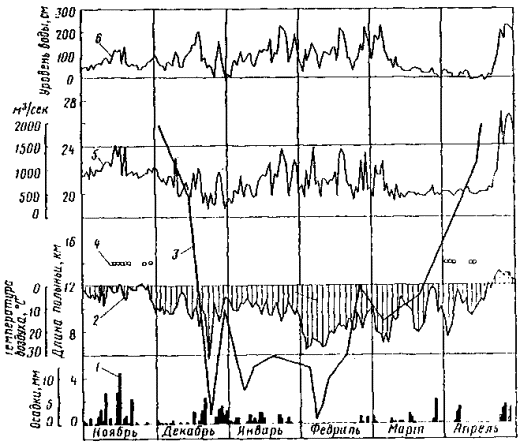
Первые ледовые образования на Оби появляются в нижнем течении в виде заберегов и сала. Внутриводный лед обычно образуется в первые дни ледохода на верхнем и среднем участках реки и в небольших количествах. Однако, как показывают наблюдения на верхней Оби [46], в продолжение осеннего ледохода образование внутриводного льда может повторяться до 3-4 раз при густоте ледохода не более 6 баллов. Образованию внутриводного льда способствует ветер, который усиливает перемешивание воды. Плывущие по реке шуга и другие ледовые образования быстро покрываются с поверхности льдом и в дальнейшем лед нарастает за счет поверхностного ледообразования (рис. 10). Толщина слоя шуги составляет обычно 20-30 см, а кристаллического поверхностного льда перед ледоставом 15-20 см.
Рис. 10. Осенний ледоход на Оби Формирование ледяного покрова на Оби идет путем последовательного образования цепи заторо-зажоров с продвижением кромки льда снизу вверх. Основными причинами образования начальных ледяных перемычек следует считать уменьшение ледопропускной способности русла в результате роста заберегов на поворотах реки и в местах разветвлений ее на рукава. В табл. 11 приведены сроки наступления осенних ледовых явлений на Оби. Таблица 11
Подъемы уровней воды при ледоставе составляют обычно 60-100 см, что говорит о том, что зажоро-заторные явления в осенний период выражены несильно. Стеснение русла шугой и битым льдом не такое большое, как на Ангаре (рис. 11). Существенные зажорные явлении наблюдаются на верхнем участке Оби (исток - г. Камень), где подъем уровня при замерзании достигает 2 м. Создание водохранилища на Оби у Новосибирска существенно отразилось на сроках вскрытия и замерзания реки в верхнем и нижнем бьефах и характере ледовых процессов. Первые ледовые образования на водохранилище появляются в виде заберегов в те же сроки, что и на прилегающих участках реки. В дальнейшем ход ледообразования па водохранилище в значительной степени зависит от скорости ветра в районе и волнового режима водоема в этот период. В тихую морозную погоду переохлаждение воды наступает в поверхностных слоях воды, где и происходит ледообразование. Ледостав наступает дружно по всей акватории водоема без ледохода, как это наблюдалось, например, в 1948 и 1959 г.г. При этом водохранилище замерзает на несколько дней раньше реки в естественном состоянии (в 1958 г. на восемь дней, в 1959 г. на два дня). Чем интенсивнее наступает похолодание, тем больше разница в сроках замерзания реки и водохранилища. В случае сильного ветра и волнения процесс ледообразования на водохранилище протекает более продолжительное время по более сложной схеме (1960, 1961 г.г.). Возникновению ледяного покрова предшествует период переохлаждения воды на значительную глубину и образование льда и шуги. Процесс установления ледостава задерживается во времени и по площади акватории. Шуговые образования в виде шуговых ковров, ледяных дисков с трудом смерзаются при волнении между собой. Они переносятся течениями и ветром и образуют у наветренных берегов большие скопления. Так, осенью 1961 г. при господствующем в период замерзания ветре у левого берега водохранилища и плотины наблюдались забереги из шугового льда шириной до нескольких сотен метров. При снижении скорости ветра ледовые образования легко смерзаются между собой и образуется ледостав. Осенью 1960 г. ледоход на водохранилище наблюдался в продолжение шести, а осенью 1961 г. - 12 дней, причем в верхней суженной части водоема, где волновые явления выражены слабо, а скорости течения незначительны, водохранилище замерзало на 5-6 (1960 г.) и 12-15 дней (1961 г.) раньше, чем в нижней озеровидной зоне. Наблюдения показывают, что при слабом ветре в период ледообразования водохранилище замерзает по длине примерно в одинаковые сроки без ледохода. При сильном ветре верхняя суженная часть водоема замерзает значительно раньше нижней озеровидной зоны. Под влиянием поступающей из водохранилища относительно теплой воды в нижнем бьефе Новосибирской ГЭС в зимнее время наблюдается полынья. Величина незамерзающего участка в нижнем бьефе зависит от расхода и температуры воды, поступающей из водохранилища, скорости течения, морфологических особенностей русла, климатических условий сезона и других причин. Из-за непрерывного изменения гидравлических и метеорологических условий ледяная кромка находится постоянно в движении, приближаясь к гидроузлу при понижении температуры воды и воздуха и удаляясь при их повышении, в связи с чем длина полыньи меняется. Приближение ледяной кромки к гидроузлу вызывает повышение уровней воды перед сооружениями, что приводит к снижению напора на ГЭС. Гидравлические условия нижнего бьефа в зимний период определяются режимом эксплуатации ГЭС. Новосибирская ГЭС участвует в покрытии пиковой части нагрузки энергосистемы, поэтому расходы и уровни в нижнем бьефе непостоянны. Так, в ноябре-декабре 1959 г. среднесуточные расходы воды изменялись от 360 до 700 м3/сек, в январе-марте 1960 г. - от 500 до 1000 м3/сек и более. Суточное изменение уровня воды у ГЭС достигало 1,7 м, у Новосибирска, в 23 км от плотины, - 1,2 м.
Рассматривая совмещенные графики колебания уровней воды по ряду водомерных постов, расположенных в нижнем бьефе (рис. 12), можно видеть, как идет распластывание волн попусков с удалением от ГЭС. Примерно в 100 км от плотины суточное регулирование стока Новосибирской ГЭС уже практически не сказывается на величине уровня воды в реке. В настоящее время в связи с созданием плотины нет поступления ледяного материала из водохранилища в нижний бьеф. Здесь ледоход образуется самостоятельно. После того как температура воды в реке на некотором расстоянии от ГЭС достигает 0°С и несколько ниже, начинается образование льда. Лед достигает прочности, необходимой для образования ледостава, далеко от плотины. Ледовыми авиаразведками, проведенными в 1959 г., установлено, что на день замерзания водохранилища (4/XI) кромка ледостава находилась в 280 км ниже створа ГЭС. В продолжение 4-10/XI кромка ледостава приближалась к плотине со средней скоростью 40 км в сутки и 11/XI была в 25 км ниже ГЭС. К середине декабря полынья достигла минимальных размеров, кромка ледостава находилась от ГЭС в 3-4 км. В этот период наблюдались низкие температуры воздуха и наименьшие за сезон расходы воды. Положение ледяной кромки в продолжение зимы не было устойчивым; в январе-марте размеры полыньи изменялись от 8 до 18 км. Ледостав в нижнем бьефе устанавливался спокойно с начальной толщиной ледяного покрова 5-10 см, поверхность которого была менее торосистой, чем это наблюдалось ранее в естественных условиях Оби. Кромка ледяного покрова в осенний период приближалась к плотине с большой скоростью. Это происходило в результате незначительной затраты ледяного материала на образование ледостава (начальная толщина ледяного покрова в условиях регулирования стока в 2-3 раза меньше, чем в естественных условиях, и в 4-5 раз меньше, чем это возможно определить по формуле К.И. Россинского [27]) и существенного влияния заберегов. Забереги в своем росте не встречали сопротивления со стороны плывущего льда, как ранее, и в связи с запаздыванием образования ледостава имели больше времени для своего роста. Ширина заберегов была значительно больше, чем на реке в естественных условиях. Плывущие ледяные поля легко заклинивались между заберегами, образуя ледяной покров. На значительном протяжении полынья представляла собой узкий незамерзающий канал - промоину шириной 50-75 м с рядом ледяных перемычек. В начале апреля в связи с повышением температуры воздуха до 0°С и выше, когда приход тепла к водной поверхности превышает расходную часть теплового баланса, размеры полыньи интенсивно увеличиваются. К 1/V 1960 г. кромка ледостава отступила на 180 км, а на момент очищения водохранилища от ледяного покрова (16/V 1960 г.) Обь была свободна от льда до устья Иртыша. Весеннего ледохода в нижнем бьефе ГЭС по существу не было. В ледяном покрове возникали промоины и лед постепенно таял на месте. Полынья удлинялась и расширялась. Общие закономерности образования заторов льда Затором, как известно, называется нагромождение льдин в русле реки во время ледохода, вызывающее стеснение живого сечения и связанный с этим подъем уровня воды. Заторы, образующиеся во время весеннего ледохода, на реках Сибири проявляются особенно ярко, вызывая высокие подъемы уровня; при осеннем ледоходе заторы здесь обычно меньше весенних, так как массы льда, участвующие в формировании осенних ледоходов, невелики. Заторы льда на реках - сложное физико-географическое явление, трудно поддающееся изучению. О заторах обычно судят по подъему уровня и разрушениям, производимым ими. Однако к настоящему времени имеется ряд исследований, которые позволяют разобраться в условиях образования заторов и наметить удовлетворительные пути их прогнозирования. Л.Г. Шуляковский [49] указывает на четыре условия образования существенных заторов: 1) сохранение ледяного покрова или значительных ледяных полей ниже части реки, где начался ледоход; 2) достаточная прочность льда; 3) скорость течения, достаточная для подныривания и нагромождения льдин; 4) интенсивный ледоход. Коротко рассмотрим условия вскрытия рек и установим наличие перечисленных выше условий для образования заторов па водотоках Сибири. Вскрытие рек - в основном результат одновременно развивающихся процессов разрушения ледяного покрова под воздействием тепла и прибывающей воды. Приток тепла к ледяному покрову зависит от метеорологических условий, наблюдающихся на данном участке речной долины, и радиационных свойств льда на этом же участке реки. Подъем же уровня воды на данном участке реки - результат снеготаяния и стекания талых вод как на окружающей местности, так и во всем бассейне. Так, например, на реках Сибири уровни поднимаются зачастую вследствие таяния снега в верхних частях бассейна, на значительном расстоянии от участка, где ледяной покров сохраняет еще значительную прочность. С повышением уровня воды ледяной покров отрывается от берегов и часто представляет собой до начала подвижек целое, не разделенное трещинами ледяное поле, находящееся на плаву. Одновременно на реке быстро растут закраины. Благодаря увеличению влекущей способности потока и уменьшению прочности ледяного покрова и его сцепления с берегами на том или ином участке реки происходит подвижка льда. Одно из условий, благоприятствующее подвижке льда, - подъем уровня по отношению к наивысшему уровню и период ледостава (Н2) как минимум на величину ∆Н = H1 - Н2 = ρлhл, где H1 - наинизший уровень воды при подвижке (в данном году); hл, ρл - соответственно толщина ледяного покрова и относительная плотность льда [4]. Например, для среднего Енисея величина весеннего превышения уровня составляет 1-1,5 м. Обычно происходит несколько подвижек льда. Ледяной покров при первой подвижке наползает на берег, отмели, острова и сохранившийся ниже по течению ледяной покров. Встретив препятствие, ледяные поля обычно останавливаются, причем ниже по реке ледяной покров сохраняется, а выше района подвижки возникает участок, свободный от льда. Образуется, как отмечает И.Я. Лисер [30], слабо выраженный затор, выше которого происходит некоторое накопление речных вод. Вследствие дальнейшего роста уровня, накопления воды выше кромки и ослабления ледяного покрова происходят подвижки льда ниже по реке. Создаются условия для вскрытия вниз по течению. При подвижках ледяные поля приходят в движение, разрушаются на части и лед сплошной массой движется по реке. Так начинается ледоход. Распространение весеннего ледохода на большинстве рек Сибири связано с перемещением вниз по течению волны весеннего половодья. Весенний ледоход начинается до наступления вершины волны паводка. Но на отдельных участках реки может сохраниться ледостав с еще прочным ледяным покровом. Этот участок реки и является обычно очагом затора. И.Я. Лисер указывает, что на формирование очага затора решающее влияние оказывают условия замерзания реки. В местах образования зажоров на реках Сибири нарастает мощный и прочный ледяной покров, обычно хорошо смерзшийся с берегами. Наблюдения показывают, что весной на участках с зажорами лед ослабляется незначительно, а подъем уровня меньше, чем на прилегающих участках реки. Поэтому здесь и образуются обычно очаги затора, что типично для рек Сибири. Очаг затора может возникнуть также при интенсивном ледоходе в результате остановки и заклинивания ледяных полей и в других случаях. Ледяной материал с вскрывшегося участка реки подходит к ледоставному участку и здесь образуются скопления льда, которые и формируют затор. На формирование затора существенное влияние оказывают скорости течения и интенсивность ледохода. С.С. Филлимонов [48], проводивший исследования лесоледоудерживающих запаней, определил критическую скорость, при которой нарушается устойчивость ледяного покрова и начинает происходить подныривание льдин под кромку. По данным его исследований, при средней скорости течения менее 0,6 м/сек лед располагается в запани (или заторе) в один слой. При скорости течения 0,75 м/сек отдельные льдины начинают ребриться и подныривать под кромку, а при скорости 1 м/сек формируется многослойный затор. Канадские специалисты Е. Паризе и Р. Хаузер [40], исследуя образование ледяного покрова на реках, предложили зависимость между скоростью потока v и толщиной льдины hл, которая будет устойчивой при подходе к кромке ледяного покрова. Эта зависимость имеет вид
где К - коэффициент формы, изменяющийся в пределах от 0,7 до 1,2; g - ускорение силы тяжести; ρ, ρл - удельные веса воды и льда. Используя эту форму для рек Сибири, где толщина льда в период весеннего ледохода порядка 0,6-0,8 м, И.Я. Лисер получил критическое значение скорости, равное 1,2-1,5 м/сек. При скорости течения больше указанной льдины не будут устойчивыми и, следовательно, возможно образование заторных скоплений льда. Из приведенных данных можно заключить, что критическая скорость, необходимая для образования затора, лежит где-то в пределах 1-2 м/сек. Величина этой скорости, очевидно, зависит от местных условий и, в частности, от величины водного объекта. На крупных реках Сибири скорости течения при ледоходе обычно выше 1 м/сек, поэтому образование заторных скоплений у ледяной кромки облегчено. В результате образования скоплений битого льда происходит стеснение водного потока льдом. Уровень воды повышается, образуется подпор, который приводит к понижению скорости потока перед кромкой. После того как на некотором удалении от очага затора скорость течения окажется ниже критической, льдины к кромке затора будут подплывать спокойно без уплотнения (рис. 13).
Рис. 13. Схема затора: 1 - остановившиеся ледяные поля; 2 - заторные массы льда; 3 - сохранившееся ледяное поле Существенное влияние на процесс заторообразования оказывают суровость зимы и условия весеннего периода. В суровую зиму образуется мощный ледяной покров (на реках Сибири это обеспечено каждый год), при дружной весне происходит быстрый рост уровня воды в водотоках. Реки вскрываются при наличии прочного ледяного покрова, что в совокупности со значительными скоростями течения обусловливает интенсивный ледоход. Существование затора в данном месте не препятствует вскрытию реки на нижележащем участке. Ниже очага затора может наблюдаться ледоход, его прекращение и возникновение других очагов затора. Разрушение затора происходит под влиянием тепловых процессов и воздействия водного потока. Лед в заторе ослабевает, отрывается от берегов, всплывает и начинает двигаться. Иногда возникают подвижки льда в заторе, что может привести к его усилению. Затор может разрушаться и вследствие высоких скоростей течения и образования промоин, по которым сплавляются вниз массы битого льда. Заторы наносят существенный ущерб народному хозяйству. Льдом разрушаются речные и прибрежные сооружения, затопляются большие территории. Поэтому очень важно заранее предвидеть места образования заторов и их величину и обеспечить мероприятия по борьбе с заторами. В настоящее время существует ряд предложений по прогнозированию возможности заторообразования и величины максимального уровня [17, 31, 35, 49, 50]. И.Я. Лисер, например, прогнозирует места образования заторов исходя из решающего влияния условий замерзания рек на формирование очага затора. Им установлено, что при высоких уровнях ледостава, а также если при замерзании реки наблюдались подвижки льда, следует ожидать весной сильный или средний затор. Величину максимального заторного уровня рекомендуется определять совместным учетом условий замерзания, суровости зимы, интенсивности весенних процессов. Однако задача прогнозирования количественных характеристик затора с должной точностью еще не решена. Поэтому заторы часто оценивают по трехбалльной шкале: слабые, средние, сильные. Заторы на реках Сибири Река Ангара. Вскрытие Ангары обусловливается влиянием озера Байкал, общим направлением течения реки с юга па север, половодьями на притоках, морфологическими особенностями русла и метеорологическими факторами. На верхнем участке реки заторы обычно невелики и не вызывают значительных подъемов уровней. Здесь Ангара вскрывается сравнительно спокойно под влиянием тепловых факторов, усиливающихся наличием полыньи. На среднем н нижнем участках заторные весенние уровни на многих пунктах наблюдений являются высокими годовыми уровнями, превышающими зажорные. Исследованию ледотермического режима Ангары, как указывалось выше, уделено большое внимание. Но из-за трудности получения исчерпывающих материалов, характеризующих заторообразования, заторные явления на реке изучены недостаточно. Река Енисей. Впервые заторные явления на Енисее были описаны Е.В. Близняком в 1915, 1916 г.г. [8, 9]. Им был собран обширный материал, характеризующий ледовый режим реки на большом протяжении. В последние годы изучением весенних ледоходов и образованием заторов на этой реке занимался И.Я. Лисер [30, 31]. Поэтому о заторах на Енисее мы располагаем наиболее полными материалами. В 1941 г. на Енисее в районе Красноярска произошел катастрофический затор льда, принесший большие бедствия. Подвижки льда произошли 30/IV при высоком уровне воды и причинили серьезные разрушения. Через 6 ч после начала ледохода ниже города образовался затор льда. В ночь на 1/V уровни воды достигли максимальных, превышающих более чем на 0,5 м самое высокое половодье в 1916 г. Затор и необычайно высокие уровни воды удерживались свыше четырех суток. Анализируя заторность Енисея у Красноярска, И.Я. Лисер [31] показал, что повторяемость существенных заторов составляет примерно один раз в четыре года. Наивысший заторный уровень является обычно и наивысшим годовым уровнем. Очаги заторов располагаются в пределах островов, находящихся на Ладейском перекате и двойном повороте русла в 19-35 км ниже города. Образование заторов может происходить и в других местах. Так, в 1947 г. сильный затор на Енисее наблюдался выше Красноярска. После суровой зимы 1946/47 г. весна наступила рано и была дружной. Вскрытие рек началось раньше обычного при еще сохранившемся толстом и прочном ледяном покрове. 17/IV граница весеннего ледохода подошла к району Красноярска, но вследствие образования затора льда в 20 км выше города, распространение ледохода вниз по реке прекратилось. Этот затор был самым продолжительным (девять суток) на среднем Енисее. Наиболее сильные заторы на Енисее отмечаются на участке Назимово-Ворогово, где в большинстве лет заторные уровни являются наивысшими годовыми. У пяти пунктов - Кызыла, Красноярска, Казачинского, Ярцево, Ворогово - самый высокий уровень за период наблюдений вызван заторными явлениями. Катастрофический затор наблюдался на Енисее у г. Кызыла в 1945 г. [2]. Зима 1944/45 г. была здесь исключительно холодной и малоснежной. Ледяной покров вследствие суровости зимы и зашугованности русла реки достигал у берегов толщины 3 м. Дружная и ранняя весна обеспечила интенсивное нарастание паводка. Непосредственно ниже г. Кызыла 20/IV начались нагромождения льда. К 23 ч уровень воды в реке повысился на 3 м. Выше города вода прорвала береговую оградительную дамбу и устремилась на городскую территорию. Наводнение продолжалось около трех дней и причинило большой ущерб городскому хозяйству. Наивысший уровень при заторе превысил на 1,3 м ранее наблюдавшийся максимум. Известны заторы у Казачинска в 1941, 1955 г.г., Енисейска в 1915, 1953 г.г., Ворогово в 1939 г., Туруханска в 1957 г. и др. В 1909 г. на Енисее ниже впадения Ангары затор вызвал подъем уровня воды за сутки около 12 м [16]. Мощные заторы наблюдаются и в низовье Енисея. Река здесь вскрывается при механическом воздействии волны половодья на почти не ослабленный таянием ледяной покров, средняя толщина которого составляет 1,4-1,5 м. В период подвижек ледяного покрова на берегах образуются нагромождения льда высотой 10-15 м и более. Надвигающийся лед часто разрушает прибрежные строения, подъездные пути и др. Один из мощных ледоходов в районе г. Дудинки описан В.А. Госсманом [19]. Первая подвижка произошла 5/VI 1959 г. при подъеме уровня на 5,6 м над уровнем, наблюдавшимся в конце зимы. Всего было отмечено четыре подвижки при непрерывном подъеме уровня воды. Ледяные поля нагромождались на берегах, и общая высота навалов у правого берега составила 15-20 м над дном реки. Ледоход начался 7/VI, a 8/VI уровень достиг отметки, наивысшей за весь многолетний период наблюдений. Величина подъема уровня составила примерно 15 м. В работе М.И. Зотина [23] указывается, что ежегодно от Туруханска до Усть-Енисейского порта образуется 7-8 заторов. Река Обь. Образование заторов характерно для верхней части Оби. Здесь в результате раннего половодья на притоках вскрытие реки начинается еще при наличии прочного ледяного покрова. Известны заторы льда у Барнаула [1903, 1937, 1941, 1958 г.г. и др.], где очаг образования затора расположен на крутом повороте реки в нижней части города. До постройки Новосибирской ГЭС заторы льда часто наблюдались у Новосибирска. Очаг затора располагался ниже города в районе Медвежьих островов. Наиболее известен затор 1920 г., когда подъем уровня над зимним горизонтом составил 10,5 м. Вода заливала всю пойму и пониженную часть города. Наводнение причинило большие убытки, особенно пароходству. В среднем течении Оби также наблюдаются заторы льда. Но заторные подъемы уровня не превышают паводковые. Наиболее известны заторы, возникающие ниже впадения р. Томи, у с. Молчаново. В нижнем течении Оби сильных заторов льда не отмечено. Заторные явления на других крупных реках. Заторы льда наблюдаются и на других крупных реках Сибири. Например, заторы льда на Томи повторяются ежегодно [17, 36, 50]. Довольна часто они образуются на Иртыше. Так, в 1928 г. в районе Омска наблюдалось сильное наводнение, вызванное заторами льда. М. В. Мясников сообщает [37], что заторы льда часто образуются ниже Омска, выше Павлодара и у многих других пунктов. Обстоятельное исследование заторных явлений на Лене провел М. К. Федоров [47]. На общем протяжении реки в 3891 км им указано 51 место обычного образования заторов. Влияние строительства ГЭС на характер заторных явлений. При строительстве ГЭС на сибирских реках встречаются трудности пропуска льда через гребенку плотины. Полагают, что, значительно стесняя естественное русло реки (в пять и десять раз) сооружением при малых пролетах между бычками плотины (12-20 м), может возникать остановка льда и образовываться затор со значительным подъемом уровня. Это обстоятельство, учтенное, в проектах организации работ, приводило к удорожанию строительства. Наблюдения лаборатории ледотермики Транспортно-энергетического института Сибирского отделения AН СССР за пропуском льда в створах строящихся Усть-Каменогорской, Новосибирской, Братской и Красноярской ГЭС (табл. 12) показали, что существенных заторов в период пропуска льда через сооружения не образуется, хотя русло реки стеснено сооружениями в четыре и десять раз, а ширина водопропускных пролетов составляла всего 12-20 м. Это объясняется существенным ослаблением льда вследствие запаздывания вскрытия реки перед сооружениями, большими скоростями течения у гребенки плотины и на подходе к ней. Ледяной покров сильно разрушался на кривой спада при подходе к плотине (рис. 14 и 15), а перед перемычкой создавались большие навалы льда (рис. 16).
Рис. 14. Пропуск льда через гребенку плотины Братской ГЭС (I0/V 1960 г.)
Рис. 15. Пропуск льда через плотину Усть-Каменогорской ГЭС Плотины гидроэлектростанций, как уже указывалось, вносят существенные изменения в ледовый режим реки. Водохранилища очищаются от льда позднее неподпертых участков рек на 10-15 дней. Замедленное вскрытие водохранилищ служит причиной формирования в зоне выклинивания подпора ледяных заторов [28]. Высота подъема уровней воды, вызванного затором в хвосте водохранилища, мало отличается от заторных повышений горизонтов в бытовых условиях. В нижних бьефах водохранилищ реки вскрываются спокойно и раньше, чем в естественном состоянии реки [46].
Рис. 16. Навалы льда перед перемычкой плотины Красноярской ГЭС (весна 1962 г.)
Весенние заторы льда на большом протяжении нижнего бьефа не образуются. Здесь следует ожидать образования заторов при больших попусках воды из водохранилищ в зимнее время. ЗАКЛЮЧЕНИЕ Исследованием общих закономерностей образования заторов и зажоров на крупных водотоках Сибири выявлено, что высокие скорости течения, ступенчатый продольный профиль и морфология русла рек, общее направление течения их с юга на север и суровые климатические условия - основные факторы, определяющие масштабы и характер образования заторов и зажоров на сибирских реках. Зажорные явления ярко выражены на Ангаре, для которой характерны пороги и шиверы с большими скоростями течения, значительные и устойчивые расходы воды в осенне-зимний период. Заторные явления наиболее сильны на Енисее, вскрытие которого происходит под влиянием перемещении вниз по течению волны весеннего половодья при еще сохранившемся прочном ледяном покрове и значительных скоростях течения. Районы образования заторов и зажоров не случайны, а определяются совокупностью ряда причин. Это обстоятельство позволяет заблаговременно предвидеть места образования заторов и зажоров, а также приближенно оценить величину подъема уровня воды, что имеет важное значение для народного хозяйства. При изучении образования заторов и зажоров на реках встречается ряд трудностей, которые преодолимы при сочетании натурного и лабораторного методов исследования. ЛИТЕРАТУРА 1. Альберг В.Я. Подводный лед. ГОНТИ, М.-Л., 1939. 2. Ануфриев В.Е. Защита населенных мест от затопления. М., изд-во Мин. ком. хоз. РСФСР, 1958. 3. Аполлов Б.А. Гидрологические информации и прогнозы. М., Гидрометеоиздат, 1945. 4. Аполлов Б.А., Калинин Г.П., Комаров В.Д. Гидрологические прогнозы, М., Гидрометеоиздат, 1960. 5. Бахтин Н.П. Река Енисей. М., Гидрометеоиздат, 1961. 6. Бибиков Д.Н., Петруничев Н.Н. Ледовые затруднения на гидростанциях, М, Госэнергоиздат, 1960. 8. Близняк Е.В. Енисей от Минусинска до Красноярска. Материалы для описания русских рек и истории улучшения их судоходных условий, ч. II, Спб., 1915. 9. Близняк Е.В. Енисей от Красноярска до Енисейска, ч. II, Спб., 1916. 10. Бутягин И.П. Прочность ледяного покрова в ледовых нагрузках на сооружения. Труды ТЭИ СО АН СССР, вып. XI, Новосибирск, 1961. 12. Быдин Ф.И. Зимний режим рек и методы его изучения. Исследование рек СССР, вып. V. Изд. Гос. гидрологического института. Л., 1933. 16. Великанов М.А. Гидрология суши, М., Гидрометеоиздат, 1948. 17. Волков И.И. Особенности весеннего ледоходного режима западно-сибирских рек на примере р. Томи, Журнал геофизики, IV, № 2 (12), 1934. 22. Естифеев А.М. Регулирование шугового потока на гидроэлектростанциях, М., Госэнергоиздат, 1958. 29. Латышенков А.М. Исследования ледозащитных запаней, «Гидротехническое строительство» № 4, 1946. 31. Лисер И.Я. Весенние заторы льда на среднем Енисее. Труды Транспортно-энергетического института Зап.-Сиб. филиала АН СССР, вып. VII, Новосибирск, 1958. 32. Лисер И.Я. О начальной толщине льда на Енисее в районе Красноярска. Труды ТЭИ СО АН СССР, вып. XI, 1961. 33. Макеров Н.С. Устройство и эксплуатация водоприемных сооружений на реках Сибири, М., изд-во Мин. ком. хоз. РСФСР, 1957. 34. Маккавеев В.М. О движении водного потока при наличии льда. Труды I Всесоюзного съезда НИТО гидравликов и гидротехников, М., Энергоиздат, 1934. 35. Максимович Н.М. Условия ледохода и борьба с заторами на р. Висле. XI съезд русских деятелей по водным путям, СПБ, 1904. 36. Марусенко Я.И. Ледовый режим рек бассейна Томи, Изд. Томского университета, 1958. 38. Нежиховский Р.А. Расчеты и прогнозы стока шуги и льда в период замерзания рек. Труды ГГИ, вып. 103, М., Гидрометеоиздат, 1963. 39. Образовский А.С. Гидравлика водоприемных ковшей. М., Госстройиздат, 1962. 40. Паризе Е., Хаузер Р. Образование ледяного покрова на реках. Доклад на VIII конгрессе международной ассоциации по гидравлическим исследованиям. Гидравлические исследования. М., Госэнергоиздат, 1962. 41. Пиотрович В.В. Появление, рост и исчезновение льда на реках ETC. Труды ЦИП, вып. 6, Гидрометеоиздат, М., 1948. 42. Потапов В.М. Ледовый режим деривационных сельских гидроэлектростанций, Госстройиздат, М., 1955. 44. Рымша В.А. Ледовые исследования на реках и водохранилищах. М., Гидрометеоиздат, 1959. 45. Самочкин В.М. Воздействие ледоходов на береговые откосы и сооружения. Труды ТЭИ СО АН СССР, вып. XI, Новосибирск, 1961. 46. Самочкин В.М. Ледотермический режим верхней Оби в естественном и регулируемом состоянии. Труды НИИЖТа, вып. XLIV, Новосибирск, 1965. 47. Федоров М.К. Заторные и зажорные явления и их развитие на р. Лене, Труды АНИИ, т. 204, Л., 1956. 49. Шуляковский Л.Г. О заторах льда и заторных уровнях при вскрытии рек. Журнал «Метеорология и гидрология» № 7, 1951. Инж. В.К. ТРОЙНИНК ВОЗДЕЙСТВИЮ ЗАЖОРНЫХ МАСС НА ОПОРЫ МОСТОВМногие реки Советского Союза отличаются особой шугоносностью в осенний период; на участках рек с высокой скоростью течения образуется большое количество шуги, которая, скапливаясь, образует зажоры. При образовании зажоров русло стесняется, изменяется уклон свободной поверхности потока на участке зажора, поднимается уровень воды перед верховой кромкой. Изменение гидравлического режима реки вызывает подъем уровня, пойменная часть реки затопляется паводком иногда катастрофических размеров. Если причиной образования зажора послужили инженерные сооружения, зажорное тело оказывает механическое воздействие, сопровождающееся иногда частичным или полным разрушением сооружения. Так, при строительстве моста через одну из рек в Северо-Западном районе СССР в результате образования зажора были повреждены временные сооружения опор моста. В 1942 г. в Сибири был разрушен понтонный мост в период шугохода. Известны и другие случаи повреждения сооружений. Вопросы механизма образования зажора и воздействия раздробленного ледяного поля на сооружения изучаются советскими и зарубежными специалистами [1-6, 9]. Значительный вклад в разработку вопроса воздействия раздробленного ледяного поля на инженерные сооружения внесли советские ученые В.П. Берденников, К.Н. Коржавин, А.М. Латышенков, А.С. Офицеров и др. Однако до настоящего времени вопросы воздействия зажорных масс на опоры мостов не получили полного разрешения. Физическая картина воздействия зажорных масс на сооружения С наступлением похолодания в осенний период в результате переохлаждения воды в реке может образоваться внутриводный лед в виде рыхлой губчатой массы, которая, всплывая и смешиваясь с кристаллами льда поверхностного происхождения и атмосферными осадками (снегом), образует шугу. Очевидно, от преобладания того или иного компонента, входящего в состав шуги, физико-механические свойства ее будут различны. При значительном поступлении снега в реку и интенсивном образовании внутриводного льда свойства шуги будут в некоторой степени соответствовать свойствам снега, погруженного в воду. По-видимому, изучение механических свойств смеси свежевыпавшего снега с фирном, может быть, в первом приближении использовано при оценке механических свойств шуги и величины силы взаимодействия зажорной массы с инженерными сооружениями. С целью получения физической картины разрушения зажорной массы и оценки механической прочности ее в лаборатории кафедры «Гидравлика и водоснабжение» НИИЖТа в марте-апреле 1965 г. были проведены опыты по разрушению снежного ковра, погруженного в воду. Установка, на которой проводили опыты, состоит (рис. 1) из гидравлического остекленного лотка шириной 40 см и высотой 60 см. Нижний конец лотка перекрыт доской высотой 30 см с отверстиями для пропуска троса. Испытуемый образец помещали между доской и штампом, нагрузка на который создавалась весом бака, заполняемого водой из водопровода. Размеры образца 20´6040 см, размеры штампа 20´20 см. Фирновый снег с крупностью зерен 1-3 мм перед укладкой тщательно разрыхлялся и помещался в лоток; на открытую горизонтальную поверхность такого образца наносили прямоугольную сетку размером 4´4 см. Водой, охлажденной до температуры, близкой к 0°С, наполняли лоток до момента всплывания снежного ковра.
Рис. 1. Схема установки: 1 - лоток; 2 - штамп; 3 - снег; 4 - трос; 5 - блок; 6 - кран; 7 - груз Создавая заполнением воды из водопровода в бак нагрузку, ее постепенно и равномерно увеличивали от нулевого до разрушающего значения. Отмечено, что с момента приложения нагрузки снег как под штампом, так и во всем массиве начинал деформироваться, а при постоянной нагрузке отмечалось пластическое течение. Нанесенная на поверхность прямоугольная сетка искривлялась, правильные квадраты деформировались в фигуры, напоминающие ромбы с криволинейными сторонами (рис. 2). При нагрузках, близких к разрушающим, снег под штампом выкрашивался и образовывалась продольная трещина, распространяющаяся по оси лотка на всю толщину образца. В большинстве случаев образец разрушался, прорезаясь с резким продвижением штампа (рывком).
Рис. 2. Схема искривления прямоугольной сетки образца: 1 - первоначальный размер образца; 2 - штамп; 3 - трещины; 4 - деформированный образец При нагрузках, близких к разрушающим, наблюдалось выкалывание части снежного ковра в виде раковины толщиной, равной примерно 2 см, а также образование опережающей трещины, распространяющейся на всю толщину образца; деформация прямоугольной сетки указывала на сложный характер распределения напряжений. Под действием нагрузки образец из разрыхленного состояния превращался в своеобразный монолит, перед штампом образовывалось уплотненное ядро, напоминающее призму с треугольным основанием и углом заострения, близким к 90°. Уплотнение ядра было столь значительно, что его можно было рассматривать как продолжение штампа, состоящее из монолитного льда. По-видимому, уплотненное ядро облегчает разрушение образца. Следовательно, разрушение шуги представляет собой явление, в некоторой степени аналогичное разрушению грунтов. При разрушении образцов шуги и грунта наблюдаются по существу одни и те же явления: образование тела повышенного давления (уплотненного ядра) при нагрузках, близких к разрушающим, наблюдается образование поверхностей скольжения и опережающей трещины и другие явления. Однако в отличие от грунтов в шуге, состоящей из частиц льда, обладающих меньшей прочностью и большей пластичностью, при приложении нагрузки к ней обнаруживаются значительно большие деформации, чем в грунте. Возможные расчетные схемы Поскольку поведение зажорной массы под нагрузкой в некоторой степени аналогично сыпучему телу (грунту), то при выборе расчетной схемы воздействия на инженерные сооружения возможно проводить аналогию с воздействием сыпучего тела. В зависимости от типа сооружения, вызвавшего зажор в реке, могут быть рассмотрены следующие расчетные схемы воздействия зажорной массы: 1) на сооружение большой протяженности (ледовые перемычки); 2) на отдельно стоящую в русле реки опору; 3) на группу отдельно стоящих в русле реки опор; 4) на берега. Рассмотрим некоторые из этих четырех расчетных схем. Воздействие зажорной массы на сооружение большой протяженности (ледовую перемычку) Общие зависимости. В некоторых случаях причиной образования зажора может быть ледовая перемычка, образующаяся в результате замерзания реки на плесовом участке [1, 5, 4]. Механизм образования зажора и воздействие его на ледовую перемычку - сложное явление, зависящее как от физико-механических свойств шуги, так и от гидравлических, геоморфологических и метеорологических факторов. В целях упрощения задачи рассмотрим воздействие зажорной массы на ледовую перемычку в призматическом русле прямоугольного сечения при равномерном движении воды. Будем считать, что нам задана ширина реки В, скорость потока v, глубина его Н и средний уклон iз, после сформирования зажора. Выберем систему координат X0Y (рис. 3) и направим ось X-X вдоль одного из берегов реки, а ось Y-Y расположим на верховой кромке зажора. На расстоянии х от начала координат вырежем участок зажорной массы длиной dx и шириной В.
Рис. 3. Расчетная схема воздействия зажорной массы на перемычку При определении сил, действующих на выделенный объем, примем следующие обозначения: f1 - коэффициент сопротивления трения воды по нижней поверхности зажорной массы; f2 - коэффициент сопротивления формы; f3 - коэффициент сопротивления трения воздуха по верхней поверхности зажорной массы; v1 - скорость воды под телом зажора; v2 - скорость на верховой кромке зажора (в сечении по оси Y-Y); v3 - скорость ветра; ω - площадь выделенного объема зажорной массы, на которой возникают силы трения от воды; ω2 - площадь миделева сечения; ω3 - площадь выделенного объема зажорной массы, на которой возникают силы трения от ветра; В - ширина реки; h - толщина слоя шуги в зажоре; iз - средний уклон поверхности зажорной массы в зажоре; qx - напряжение в теле зажора в сечении х; qy - напряжение в теле зажора в сечении, перпендикулярном оси X-Х; τ - касательные напряжения, действующие в месте соприкасания зажорной массы с берегами: τ = qytgφ0 + c с - сцепление зажорной массы с берегами; φ0 - угол внутреннего трения зажорной массы; γш - объемный вес зажорной массы. Рассмотрим равновесие выделенного объема под действием следующих сил: 1. Гидродинамическое воздействие потока на нижнюю поверхность зажорной массы R1 = f1ω1v12 = f1Вv12dx. 2. Лобовое воздействие потока при х-0 R2 = f2ω2v22 = f2Вhv22. 3. Горизонтальная составляющая силы тяжести зажорной массы R3 = γшBhiзdx. 4. Давление зажорной массы на выделенный объем на расстоянии х от начала координат R4 = qxBh. 5. Давление зажорной массы на выделенный объем на расстоянии x + dx от начала координат R5 = (qx + dqx)Bh. 6. Воздействие ветра на поверхность выделенного объема R6 = f3ω3v32 = f3Вv32dx. Воздействие от ветра принято наибольшее, т.е. рассмотрен случай, когда направление ветра и течения воды в реке совпадают. 7. Сила трения зажорной массы о берега
где Г.Н. Покровский [7], пользуясь методами статистической механики, установил зависимость для коэффициента бокового давления сыпучих тел
Подставляя величину коэффициента бокового давления в уравнение для силы трения зажорной массы о берега, после преобразования получим T = 2(1 - 0,74 tgφ0)tgφ0hqxdx - 3,04 tgφ0hcdx + 2 chdx Проектируя все силы на ось X-X, получим
В уравнение (1) сила лобового воздействия не входит, так как она непосредственно на выделенный объем не действует, а ее эффект учитывается напряжением qx в зажорной массе. Разделив уравнение (1) на Bhdx, после преобразования получим
Для сокращения записи введем новые обозначения:
и представим уравнение (2) в следующем виде:
Общее решение дифференциального уравнения (3) будет
При х = 0, qx= f2v22 частное решение будет иметь вид
где е - основание натуральных логарифмов. Если х значительно больше В, максимально возможное давление будет
подставляя значения А и D, имеем
Суммарная нагрузка на перемычку составит Определение давления зажорной массы на ледовую перемычку в предположении образования разгружающего свода. Как известно, на сооружение, расположенное в толще грунта на большой глубине, давит не весь вышележащий грунт, а только часть его. Для определения давления на сооружения, глубоко расположенные в грунте (тоннели), широко применяют теорию образования разгружающего свода, разработанную М.М. Протодьяконовым. Согласно этой теории в толще грунта образуется разгружающий свод, который воспринимает давление от вышележащих слоев сыпучего тела, а на сооружение оказывает давление лишь масса грунта, расположенная ниже разгружающего свода. Принимается, что нагрузка на свод от вышележащих слоев грунта равномерно распределена по длине пролета свода, а так как сыпучее тело не сопротивляется действию растягивающих усилий, очертание оси свода принимает форму квадратной параболы. Применяя теорию М.М. Протодьяконова для определения давления на ледовую перемычку, будем полагать, что в русле реки образуется как бы разгружающий свод, который опирается на берега и благодаря силам трения зажорной массы о берега находится в состоянии равновесия при действии на него зажорных масс, расположенных выше по течению (рис. 4).
Рис. 4. Схема разгружающего свода, расположенного в русле реки Для определения реакций опор и стрелы свода разрежем его вертикальной плоскостью, проходящей по оси потока, и отбросим верхнюю часть. Воздействие отброшенной части заменим силой Н. Для оставшейся нижней части свода напишем уравнения равновесия, имея в виду, что сила давления R = Pf, где f - коэффициент трения зажорной массы о берега. Итак, уравнения равновесия будут: 1) сумма проекции всех сил на ось Y-Y Р - H = 0, откуда Р = H 2) сумма проекций всех сил на ось X-X
откуда
3) сумма моментов всех сил относительно точки 0
откуда
Как отмечалось ранее, давление на перемычку создается воздействием зажорной массы, расположенной ниже разгружающего свода. Учитывая, что разгружающий свод, образованный сыпучим телом, способным принимать под действием нагрузки определенный естественный откос, не может иметь постоянного сечения, то стрела подъема нижней грани разрушающего свода будет больше стрелы подъема оси свода на величину заложения естественного откоса с высотой сыпучего тела, равного половине ширина водотока (рис. 5).
Рис. 5. Схема нижней грани и осп разгружающего свода: 1 - ось свода; 2 - нижний грань свода; 3 - ледовая перемычка; а - половина высоты свода в замке Выражение для стрелы подъема нижней грани разгружающего свода запишется так
где a - угол естественного откоса. Угол естественного откоса для сыпучих тел [7] с достаточной степенью точности для практических расчетов может быть принят равным углу внутреннего трения. Окончательное выражение для стрелы подъема нижней грани разгружающего свода примет вид
Давление на ледовую перемычку по аналогии с теорией М.М. Протодьяконова определится величиной, пропорциональной объему зажорного материала, расположенного за нижнем гранью разгружающего свода, где k - коэффициент пропорциональности, учитывающий суммарное воздействие воды, ветра и горизонтальной составляющей силы веса зажорной массы, отнесенной к единице объема. Заметим, что формулы (6) и (8), полученные различными методами, идентичны. В самом деле, полагая
получим полное их совпадение. Ввиду того что нагрузка на ледовую перемычку пропорциональна объему тела, ограниченного параболической поверхностью, то и интенсивность ее распределения по длине пролета перемычки будет меняться тоже по параболическому закону. Воздействие зажорной массы на опоры Воздействие на группу опор. Предполагая, что перед опорами моста образуется ряд разгружающих сводов (с пролетами, равными пролетам моста), опирающихся на эти опоры, разгружающие своды создают своеобразную перемычку, воспринимающую давление от вышележащих зажорных масс и передающих его опорам. Суммарное давление на промежуточные опоры, расположенные в русле реки шириной В, определится как давление на ледовую перемычку по уравнению (6) или (8) в зависимости от наличия исходных данных. Воздействие на одиночную промежуточную опору. Если перед опорами моста образуются разгружающие своды и интенсивность давления будет изменяться по параболическому закону, максимальное давление будет восприниматься опорой, находящейся в середине реки (рис. 6).
Рис. 6. Схема разгружающих сводов в русле реки и у опор моста: 1 - свод в русле потока; 2 - свод у опор моста; 3 - опоры; 4 - эпюра давлений на средний пролет моста Если мост имеет n-1 промежуточных опор, давление па опору, находящуюся в середине реки, составит
или, подставляя значение
в уравнение (10), после преобразования получим
где n-1 -число опор моста; Q - давление на перемычку по зависимости (6) или (8). Давление на опоры моста, возникающее при разрушении зажорной массы. Определяя давление от воздействия зажорной массы по зависимости (11), следует иметь в виду, что оно не может превысить величины, необходимой для ее разрушения. Как показывает опыт, сила, необходимая для разрушения зажорной массы, зависит от многих факторов и прежде всего от физико-механических свойств, ширины опоры в плане, толщины слоя шуги, формы опоры в плане, скорости нарастания нагрузки и т.д. Исходя из сказанного сила, необходимая для разрушения зажорной массы, может быть определена по следующей зависимости:
где Rc - предел прочности зажорной массы на сжатие, н/м2; b - ширина опоры в плане, м; h - толщина слоя шуги, м; m - безразмерный коэффициент, учитывающий форму опоры в плане, скорость нарастания нагрузки, полноту соприкасания шуги с опорой. По ориентировочным данным, полученным из опыта, предел прочности зажорной массы на сжатие может быть принят равным около 50·9,8·103 н/м2. Применение зависимостей (6), (11) и (12) рассмотрим на примере. Пример расчета. Определить давление на опору, возникающее в результате зажора в реке шириной 1000 м. Скорость воды под телом зажора 2,5 м/сек; толщина слоя шуги в зажоре 2,5 м; средний уклон поверхности шуги в зажоре iз = 0,0004; объемный вес шуги γш =0,5·9,8·103 н/м3; количество опор моста n - 1 = 19; ширина опоры в плане b = 3 м; сцепление шуги c = 0,1·9,8·103 н/м2; коэффициент трения воды о шугу f1 = 0,0005·9,8·103 н·сек2/м4; тангенс угла внутреннего трения tgφ0 = 0,3; воздействием ветра пренебрегаем. Решение Давление на перемычку по зависимости (6)
Давление на опору моста по зависимости (11)
Давление на опору моста по зависимости (12) N = 1·50·9,8·103·3·2,5 = 375·9,8·103 н. Следовательно, максимально возможное давление на опору моста составит 375·9,8·103 н. ЗАКЛЮЧЕНИЕ Ввиду некоторых допущений (равномерное движение воды в реке, призматическое русло прямоугольного сечения и др.) предлагаемый метод учета воздействия зажорных масс на перемычку следует рассматривать как первое приближение, нуждающееся в уточнении ряда факторов. К ним следует отнести такие, как толщина слоя шуги в зажоре, коэффициент трения воды о шугу, сцепление, угол внутреннего трения, объемный вес шуги в зажоре и другие факторы. Давление на опоры моста не может превышать величины, необходимой для разрушения зажорной массы, поэтому давление на опору моста может быть определено по зависимости (12). Для более обоснованного определения давления по зависимости (12) необходимо уточнить значения предела прочности при сжатии, а также выяснить влияние формы опоры в плане на величину давления. ЛИТЕРАТУРА 1. Коржавин К.Н. Воздействие льда на инженерные сооружении. Новосибирск, СО АН СССР, 1962. 2. Латышенков А.М. Исследование ледозащитных запаней. Журнал «Гидротехническое строительство» № 4, 1946. 3. Берденников В.П. Воздействие раздробленного ледяного поля па берега. Труды ГГИ, вып. 110, Л., 1964. 4. Естифеев А.М. Регулирование шугового потока на гидроэлектростанциях. М., Госэнергоиздат, 1958. 6. Паризе Е., Хаузер Р., Ганон А. Образование ледяного покрова и ледяных заторов на реках. Доклад на XI конгрессе МАГИ, Л., 1965. 7. Клейн Г.К. Строительная механика сыпучих тел. М., Госстройиздат, 1956. 8. Зеленин А.Н. Физические основы теории резания грунтов. М, 1950. Канд. техн. наук Г.Я. КУЗУБЛЕДОВЫЕ ЗАТРУДНЕНИЯ НА ВОДОЗАБОРАХ, РАСПОЛОЖЕННЫХ В НИЖНЕМ БЬЕФЕ НОВОСИБИРСКОЙ ГЭСНекоторые особенности ледотермического режима нижнего бьефа ГЭС На многих реках Сибири в осенне-зимний период наблюдается интенсивное образование шуги, сопровождающееся зажорами и повторными ледоходами. Природа образования ее достаточно выяснена. Как известно, шуга образуется в период, когда река свободна от ледяного покрова при отрицательных температурах воздуха, что приводит к переохлаждению сначала поверхностных слоев воды, а затем благодаря наличию турбулентного режима поток может быть переохлажден и по всему сечению. В переохлажденном потоке при наличии ядер кристаллизации возможно образование внутриводного льда в виде отдельных кристаллов, всплывшие скопления которых и называют шугой. В начале процесса рыхлая шуга почти не выступает из воды, а затем ее количество, плавучесть и плотность заметно возрастают. Дальнейшее продвижение ее вниз по реке приводит к образованию более крупных скоплений в виде шуговых ковров и венков. Одновременно на их поверхности образуется корка кристаллического льда, которая, нарастая, образует льдины. Образование шуги присуще главным образом .порожистым рекам с бурным течением, каменистым дном и большими скоростями. В Сибири особенно шугоносны Ангара, Енисей, Томь, Кондома, Ульба, Бия, Катунь и другие реки, в меньшей степени - Обь и Иртыш, особенно в среднем и нижнем течении. На некоторых реках шуга образуется в течение всей зимы; при наличии незамерзающих участков образовавшаяся здесь шуга, подплывал к кромке льда, легко увлекается течением под ледяной покров. Количество шуги в осенне-зимний период порой бывает так велико, что она, всплывая, идет толстым слоем, иногда заполняя большую часть живого сечения. Так, например, на Томи, Ангаре, Бии, Катуни и других реках зашугованность доходит до 75 % и более, что приводит к образованию зажоров [8], [10]. После установления ледостава процессы образования и роста шуги прекращаются. Естественно, что образование шуги, движение ее по реке мощным слоем, возникновение зажоров и осенние ледоходы могут создавать шуголедовые затруднения на водозаборных сооружениях и нарушать их нормальную работу. В связи с тем, что ледотермические процессы весьма сложны и определяются многими факторами, необходимы детальные исследования для каждой отдельной реки и каждого пункта водозабора. Рассмотрим работу водозаборных сооружении в нижнем бьефе Новосибирской ГЭС, расположенных на участке 20 30 км ниже плотины. Возведение Новосибирской ГЭС в 1957 г. и образование водохранилища (которое было наполнено до нормального подпорного уровня в 1959 г.) существенно изменили естественный режим Оби в нижнем бьефе в непосредственной близости к стволу гидросооружения. Образование устойчивого ледяного покрова в нижнем бьефе наблюдается и сейчас, но продолжительность ледоставного периода сократилась. Процессы замерзания и вскрытия реки приобрели иной характер. Образование шуги наблюдается и теперь, а в некоторые годы вследствие сочетания гидрометеорологических факторов шуговые массы достигают значительных величин. По данным съемки 17-23 декабря 1958 г. (рис. 1), слой шуги достигал наибольшей толщины 1,3 м у правого берега профиля № 23, расположенного на 6,9 км ниже ГЭС; на профиле № 45 у Новосибирска - 22,7 км ниже ГЭС, максимальная толщина шуги доходила до 2,3 м, средняя - 0,72 м; на профиле № 24 в 69 км ниже ГЭС максимальная толщина слоя шуги достигала уже 3,6 м; средняя была равна 1,63 м. По данным съемки 26 февраля-3 марта 1959 г., шуга на рассматриваемом участке почти полностью исчезла, за исключением профиля № 45 у Новосибирска, где максимальная величина ее оставалась равной 1,5 м, а средняя - 0,2 м.
Рис. 1. Ледомерная съемка 17-23 декабря 1958 г. Таким образом, можно утверждать, что в нижнем бьефе Новосибирской ГЭС образуется внутриводный лед и шуга и в отдельные годы в довольно значительных объемах. Образование внутриводного льда наблюдается, как правило, наиболее интенсивно в вечерние и ночные часы. Это может быть связано как с сокращением сброса воды ГЭС, так и с понижением температуры воздуха. На ледотермический режим нижнего бьефа оказывает существенное влияние полынья, которая сохраняется в течение всей зимы ниже плотины. Длина полыньи не остается постоянной, а меняется в зависимости от хода температуры и расхода воды, поступающего в нижний бьеф, от скоростей течения, температуры воздуха и других климатических и морфологических условий. С повышением температуры воды, поступающей из водохранилища, температуры воздуха и с увеличением расходов воды через створ ГЭС кромка полыньи отступает от плотины, а при понижении температур воды, воздуха и уменьшении расходов кромка приближается к ГЭС. Гидравлические условия нижнего бьефа в зимний период определяются неравномерным режимом работы гидротурбин ГЭС, что приводит не только к колебаниям среднесуточных расходов и уровней (рис. 2 и 3), но и к колебаниям в течение суток. Так, в зиму 1962/63 г. (с ноября по май) среднесуточные расходы воды изменились от 300 до 1790 м3/сек, а среднесуточные горизонты воды имели колебания в 2,14 м. В зиму 1963/64 г. за тот же период среднесуточные расходы изменялись от 200 до 2290 м3/сек, а колебания уровней составили 2,42 м. Суточные колебания уровней у плотины ГЭС доходили до 1,6-1,8 м. Температуру воды, поступающей в нижний бьеф, за рассматриваемый период систематически не измеряли. Имеются лишь отдельные наблюдения и данные В. М. Самочкина [3], на основании которых можно считать температуру поступающей воды в нижний бьеф равной +0,5; +1,2°С (для зимы 1959/60 г.). В начале зимы, после ледостава в водохранилище, наблюдается наиболее низкая температура воды, затем она повышается до февраля за счет прогревания воды в водохранилище, а к весеннему периоду заметна тенденция к понижению. Весной же вследствие интенсивной сработки верхнего бьефа она снова повышается. Рис. 2. Совмещенный график изменения гидрометеорологических элементов в нижнем бьефе Новосибирской ГЭС. Зима 1962/63 г.: 1 - осадки; 2 - температура воздуха; 3 - наблюденная длина полыньи; 4 - шуголедовые затруднения по датам на водозаборе «Камешек»; 5 - расходы воды в створе ГЭС; 6 - уровень воды нижнего бьефа у плотины над нулем графика. Осадки и температура воздуха по данным метеостанции с. Огурцово После сооружения ГЭС в нижнем бьефе осенний ледоход здесь образуется самостоятельно. Вода, поступающая из водохранилища, охлаждается и на некотором расстоянии от плотины приобретает температуру около 0°С, затем начинается ее переохлаждение, ледообразование и ледоход (рис. 4). Участок ледообразования и ледохода находится между нулевой изотермой, разграничивающей зоны с положительными и отрицательными температурами воды и кромкой льда, где уже наступил ледостав. В зоне переохлажденной воды образуется внутриводный лед, который, всплывая, приводит к появлению шуговых венков и ковров. Находящаяся на поверхности шуга смерзается, покрывается коркой кристаллического льда, которая, постепенно нарастая, образует льдины. Кроме того, особенно в начале льдообразующего участка, плывет сало, блинчатый лед, снежура, все это смерзается, образуются ледяные поля и более или менее мощные ледоходы. Рис. 3. Совмещенный график изменения гидрометеорологических элементов в нижнем бьефе Новосибирской ГЭС. Зима 1963/64 г. Обозначении 1-6 см на рис. 2 Весь этот ледовый материал подходит к нижней кромке полыньи, часть его подныривает под лед, а часть уплотняется, смерзается, образуя ледяной покров, и кромка полыньи перемещается вверх. Иногда кромка полыньи в связи с подъемом горизонтов воды и повышением температуры взламывается и перемещается вниз, изменяя и положение нулевой изотермы. На все изменения температуры воды и воздуха нулевая изотерма реагирует быстрее, чем кромка полыньи; ее положение определяется процессами теплоотдачи с открытой водной поверхности реки и запасом тепла в потоке. Следовательно, чем ниже температура воды и воздуха и чем меньше расход воды, тем быстрее происходит передвижение нулевой изотермы. Таким образом, как кромка полыньи, так и нулевая изотерма постоянно находятся в движении, что и определяет льдообразование и ледовой режим нижнего бьефа.
Рис. 4. Схема расположения полыньи и нулевой изотермы в нижнем бьефе ГЭС: 1 - ледяной покров; 2 - участок ледообразования и ледохода; 3 - открытая поверхность; 4 - кромка полыньи; 5 - нулевая изотерма Например, кромка полыньи (см. рис. 2 и 3) в зиму 1962/63 г. приблизилась на 3 км (7 января 1963 г.); передвижение ее к ГЭС обусловилось резким понижением температуры воздуха в ночь на 7 января. В зиму 1963/64 г. кромка льда 24 декабря 1963 г. приблизилась на 1 км, а 7 февраля 1964 г. - всего на 0,5 км от ГЭС; это можно объяснить резким уменьшением расходов с 1480 до 732 м3/сек. Кроме того, в этот период наблюдались низкие температуры воздуха: 7 февраля 1964 г. среднесуточная температура была - 25,2°С. Лед, окаймляющий полынью, в ряде случаев имеет ровную поверхность, чаще торосистую, а иногда образуются навалы льда высотой до 2 м. Форма полыньи разная; обычно это полоса, стесненная заберегами, с шириной, равной 1/3-1/5 ширины реки, реже - узкая длинная промоина, ширина которой доходит всего до 50 м. Полынья, как правило, заканчивается рядом ледовых перемычек. Ниже кромки полыньи существуют еще отдельные замкнутые полыньи разных размеров, иногда отдаленные от кромки на значительные расстояния. Полынья часто наблюдается у водозабора «Камешек» ближе к левому берегу. Вдоль берегов в течение всей зимы на протяжении полыньи наблюдаются забереги. Ширина их различна - по правому берегу у плотины они больше, а по левому доходят всего до 5 м. Ниже они расширяются и занимают большую часть ширины реки. Объясняется это тем, что турбины и водосливная часть плотины расположены у левого берега. Забереги образуются у берегов, где глубина и скорости невелики. Значительные колебания уровней воды в нижнем бьефе иногда приводят к образованию заберегов высотой до 2 м. Для иллюстрации ледового режима в нижнем бьефе Новосибирской ГЭС приведем некоторые записи из дневника наблюдений [9]. 5 января 1963 г. 12 ч (t°воз = -12,2°С) В нижнем бьефе имеется полынья длиной 10 км. На этом участке вдоль берегов есть забереги шириной от 5 м в начале участка и до 250 м в конце. Забереги торосистые, высота торосов до 0,5-1,0 м. Ниже д. Юный Ленинец (5,4 км от ГЭС) 2/3 ширины реки покрыты льдом; на 11 км ниже кромки льда - ледостав с отдельными полыньями, далее сплошной лед. Ледяной покров торосистый. 13 января 1963 г. 10 ч (t°воз = -10,9°С) Уровень воды низкий, начиная от с. Огурцово (3,1 км от ГЭС), по реке ледоход 8 баллов; плывет лед, который образовался в ночь на 13 января, ледяные поля достигают площади до 200 м2, толщина плывущего льда от 2 до 5 см. Кромка льда от ГЭС в 14 км. Участок реки 10-14 км постепенно забивается плывущим льдом. 17 ч. На протяжении 12 км от ГЭС на реке чисто, вдоль берегов забереги. Нижняя часть полыньи протяженностью около 2 км забита льдом. 15 января 1963 г. 14-13 ч (t°воз = -24,6°С) Вследствие резкого понижения температуры воздуха над водой стоит густой туман; на реке слышен шум от плывущего льда. Кромка льда в 13 км от ГЭС, далее ниже по реке ледостав, лед торосистый, против водозабора «Камешек» - полынья. 16 января 1963 г. 10-18 ч (t°воз = -30,6°С) На реке ледоход по всей открытой части. Плывущий лед имеет толщину 2-5 см, площади льдин достигают 50-300 м2. На 11-м километре от ГЭС плывущий лед останавливается, нижняя часть полыньи постепенно заполняется льдом, шугой, поверхность останавливающегося льда получается торосистой с отдельными навалами льда до 2 м. К 14 ч кромка льда находилась в 10 км от ГЭС. Из проведенного анализа можно заключить, что местные ледоходы в нижнем бьефе наблюдаются с момента наступления холодов и продолжаются всю зиму. Они бывают и весной (март, частично апрель) в то время, когда температура воздуха еще отрицательна. И только в апреле, в связи с повышением температуры воздуха до 0°С и выше, местные ледоходы исчезают. Так как ледовый материал из водохранилища не поступает, весенних ледоходов в обычном смысле слова, которые были раньше на Оби у Новосибирска, в нижнем бьефе не наблюдается. Процесс вскрытия при положительных температурах воздуха начинается с появления отдельных промоин. В дальнейшем происходит разрушение ледяных перемычек, разделяющих промоины, и образование открытых каналов с последующим соединением их с полыньей. Лед постепенно тает, полынья удлиняется и расширяется за счет разрушения заберегов. Так как ледяная кромка перемещается вверх и вниз, то начало окончательного движения кромки льда вниз по течению и следует считать моментом вскрытия Оби в нижнем бьефе. Ледовые затруднения у водозаборов В нижнем бьефе Новосибирской ГЭС находится свыше десяти расположенных двумя группами водозаборов различных ведомств и предприятий. Первая группа находится ближе к ГЭС: водозабор «Камешек» на правом берегу в 14 км, левобережный городской водозабор в 15,5 км от ГЭС и строящийся ковш на .правом берегу, между водозаборами «Камешек» и левобережным. Вторая группа водозаборов, расположенных на обоих берегах Оби, находится в черте города на участке от 19-го (городской правобережный водозабор ниже устья р. Ини) до 30-го километра от створа ГЭС. Водозаборы первой группы находятся в зоне, где больше сказывается влияние гидростанции; во второй же группе ледотермический режим нижнего бьефа не так заметно влияет на работу водозаборов. Рассматривая шуголедовые затруднения на водозаборах и ледотермический режим нижнего бьефа, приходим к выводу, что затруднения возникают в период, когда река свободна от ледяного покрова и в районе водозабора наблюдается ледоход (см. рис. 4). В других случаях, т.е. когда в районе водозабора имеется устойчивый ледяной покров или водозабор находится в зоне с температурами выше нуля (выше нулевой изотермы), шуголедовых затруднений водозаборы обычно не испытывают. В связи с тем, что ГЭС меньше влияет на водозаборы второй группы, шуголедовые затруднения здесь хотя и возникают, но определяются общими ледовыми условиями Оби; влияние полыньи сказывается меньше. В этом районе ледовый покров устанавливается, но продолжительность ледостава значительно сокращается по сравнению с незарегулированной рекой. Для характеристики в таблице приведены некоторые данные по водопосту «Новосибирск» за период 1962-1964 г.г.
В период осеннего шугохода наблюдается образование внутриводного льда и шуги, которые забивают решетки водоприемников. Меры борьбы - электрообогрев, обратная промывка водоприемных водоводов, устройства шугоотбойных запаней и коробов. Шуголедовых затруднений в весенний период бывает значительно меньше и они не приносят существенных неприятностей. На многих водозаборах благодаря их удачному расположению, особенностям конструкций и своевременным мероприятиям по борьбе с шугой шуголедовых помех не бывает. Рассмотрим ледовые затруднения на самом нижнем водозаборе, находящемся в 30 км от ГЭС. Водозабор расположен на правом берегу, имеет ряжевый оголовок, вынесенный на 300 м в реку; раструбы самотечных линий ограждены решетками, на которых в начале был сделан электрообогрев. В последующем электрообогрев был снят, а прутья решетки гуммированы - покрыты слоем резины. Водозабор испытывал значительные затруднения от шуги, шуга закупоривала приемные решетки, а иногда попадала в приемные аванкамеры, что приводило к перерывам и перебоям в водоснабжении. Причина шуголедовых помех (по наблюдениям) - приносная (транзитная) шуга; образования внутриводного льда на решетках водоприемных устройств не наблюдалось. Шуга на данном участке реки идет мощным слоем, доходящим до 2 м и более, и благодаря направлению струй шуговые ковры прижимаются к оголовку. Кроме того, господствующие ветры (рис. 5), дующие с левого берега, еще больше способствуют прижатию шуги к правому берегу. С ростом заберега, как только он закрывал оголовок, шуголедовые помехи прекращались. В 1963 г. по наблюдениям водолазов осенью были забиты не только приемные решетки, но и весь оголовок был покрыт массой шуги и представлял собой, по рассказам водолазов, «гору» шуги. Скопление шуги было размыто гидропушкой, а решетки очищены обратной промывкой. Рассматриваемый водозабор начал испытывать шуголедовые затруднения после постройки ГЭС, что связано с более низкими горизонтами воды в нижнем бьефе в период осеннего ледохода. Шуга, идущая мощным слоем, захватывала оголовок. В качестве мер борьбы применяли шугоотбойники и обратную промывку. Электрообогрев нужного эффекта не давал. В настоящее время оголовок перенесен дальше в реку, находится на большей глубине и шуголедовых помех не испытывает.
Рис. 5. Расположение водозабора и роза ветров Трудно оценивать влияние ГЭС на работу водозаборов в нижнем бьефе. Некоторые водозаборы попали в более сложные условия и испытывают затруднения, для других же, наоборот, условия оказались более благоприятными. В целом шуголедовые помехи первой группы водозаборов благодаря их конструктивным особенностям, расположению и мероприятиям против шуги значительных затруднений в водоснабжении не приносят. Наиболее значительный интерес представляют работы водозаборов первой группы, расположенных в зоне влияния ГЭС. Водозабор «Камешек», левобережный городской водозабор находится всего около 1,5 км друг от друга, но благодаря расположению, морфологическим особенностям русла, а также климатическим условиям сезона условия их работы резко отличаются. Левобережный водозабор в настоящее время имеет русловый оголовок с выносом в реку на 76 м. Оголовок имеет четыре приемных окна высотой 1,25 м, верх окон расположен на глубине 1,6 м от наинизшего горизонта воды, а низ - на 0,8 м от дна. Окна ограждены металлическими решетками с электрообогревом. Через приемные окна вода по самотечным линиям поступает в приемные камеры. Хотя водозабор находится часто в одно время с водозабором «Камешек», в ледообразующем участке, однако шуголедовых помех не испытывает. Объясняется это, во-первых, расположением водозабора (см. рис. 3). Ось потока, идущая от водозабора «Камешек», ударяясь в левый берег, выше водозабора, отражается и проходит, отжимаясь от водозабора, ниже у водозабора и ниже у берега наблюдается заводь, которая быстро замерзает. Оголовок же находится в зоне потока, но плывущая шуга и снежура струями к оголовку не прижимаются. По розе ветров (см. рис. 5), которая построена по данным метеостанции с. Огурцово, находящейся на 3,1 км от ГЭС (за период ноябрь 1962 и 1963 гг., а также февраль, март 1963 и 1964 г.г., т.е. за время интенсивного шуго- и ледообразования осеннего и весеннего ледохода), видно, что господствующими ветрами являются южные и юго-западные, а они отжимают плывущую шугу от водозабора. В результате этого шуга и снежура не приносят помех водозабору. Для устранения помех от внутриводного льда, образующегося у оголовка, применен электрообогрев решеток. Обогрев решеток - эффективное мероприятие. В период редких вынужденных неполадок с обогревом сразу сокращается подача воды в камеры. Водозабор у мыса «Камешек», построенный в 1960 г., имеет ряжевый оголовок, вынесенный в реку на 137 м. Оголовок имеет три аванкамеры, из которых вода забирается тремя самотечными трубопроводами (с поднятыми вверх раструбами и с огражденными металлическими решетками с просветом 3 см). Оголовок загружен камнем, а сверху закрыт настилом. С противоположных сторон от раструба самотечной линии, т.е. с речной и береговой сторон, вода поступает в каждую аванкамеру через два окна размером 2´2 м каждое. На оголовке все шесть приемных окон, защищенных металлическими решетками с просветом в 5 см, расположены в ряже таким образом, что их верх находится на глубине 2,6 м от низких горизонтов воды, а низ - около 2 м от дна. Концы раструбов самотечных линий находятся примерно против середины приемных окон. Предусмотренный проектом электрообогрев сороудерживающих решеток как мероприятие по борьбе с внутриводным льдом пока не осуществлен. Вода по самотечным линиям поступает в аванкамеру берегового водоприемника и, пройдя плоские сетки, поступает к насосам. Сетки, две крайние с ячейками 2´2 см, а средняя 1´1 см, съемные и могут по пазам подниматься вверх. Данный водозабор очень часто и много страдает от шуголедовых помех, при этом уменьшается поступление воды в аванкамерах водоприемника, а решетки или самотечные трубы иногда полностью забиваются шугой, что вызывает остановку работы насосной станции: агрегаты выключаются из работы последовательно один за другим или по нескольку одновременно и станция останавливается. Продолжительность полной остановки станции - до 5 ч и более. В данной статье рассмотрены шуголедовые затруднения в зимы 1962/63 и 1963/64 г.г. За этот период неполадки в водоснабжении по срокам распределились следующим образом. Осенью 1962 г. в конце октября и начале ноября были срывы подачи воды. Весной 1963 г. (с 15 февраля по 20 апреля) количество остановок насосов, вызванных забивкой шугой, достигло 23. Осенью в 1963 г. затянулся осенний ледоход и ледостав наступил в районе водозабора лишь 18 декабря, за этот период было более 20 помех в водоснабжении. Весной 1964 г. помехи наблюдались в апреле. На этой насосной станции не всегда регистрировали помехи в водоснабжении, поэтому число их, вероятно, было больше указанного. Мера борьбы с шуголедовыми помехами - обратная промывка самотечных линий - давала положительные результаты. Количество промывок доходило до 6-10 в сутки, а продолжительность каждой промывки составляла 10-15 мин. Как видно из сказанного, водозабор «Камешек» испытывает значительные ледовые затруднения. Выше водозабора, у правого берега в заливе и у островов, находятся мели, которые быстро закрываются заберегами (см. рис. 5), и вся плывущая сверху шуга прижимается к правому берегу - ударяется в водозабор. Кроме того, этому способствуют господствующие в осенний и весенний периоды южные и юго-западные ветры, дующие с левого берега. На данном участке образуется внутриводный лед, а шуга движется у правого берега мощным слоем, доходящим до 2 м и более. Усугубляет шуголедовые помехи и снежура, которая во время больших метелей играет значительную роль. Из анализа помех (см. рис. 2 и 3) следует, что ледовые затруднения наблюдаются при наличии кромки полыньи ниже водозабора и часто совпадают с днями метелей, с южными и юго-западными ветрами. Юго-западные ветры, дующие под углом к течению снизу, не только прижимают снежуру и шугу к водозабору, но и сдерживают их движение, создавая подпор и тем самым увеличивая толщину слоя шуги. Известны случаи, когда даже одна снежура может доставить значительные затруднения в водоснабжении. Так, например, в ноябре 1956 г. на р. Ине (район Новосибирска), когда не было ледохода, выпало много снега и образовался мощный слой снежуры, которая забила водоприемные сооружения на водозаборах некоторых железнодорожных станций. Случаи перебоев в водоснабжении, вызванные снежурой, наблюдались и на водозаборе «Камешек» и других водозаборах нижнего бьефа Новосибирской ГЭС. На помехи оказывают влияние и неблагоприятное сочетание гидрометеорологических условий, малые расходы и низкие горизонты воды, низкие температуры воздуха и воды и др. Из сказанного следует, что помехи в водоснабжении вызываются транзитной шугой, снежурой и образующимся внутриводным льдом. Шуга и снежура, идущие мощным слоем, прижимаются и заносятся к водоприемным окнам, закупоривая решетки. Хотя на водозаборе «Камешек» решетки были поставлены на приемных окнах ряжа и раструбах самотечных линий, а в одной камере на приемных окнах не было решеток, тем не менее забивались все три самотечные линии. Следовательно, решетки забиваются на самотечных линиях; подтверждением этому служит ликвидация закупорок обратной промывкой: Промыть решетки окон водоприемных аванкамер ряжа, имеющих размер 2´2 м, невозможно. Таким образом, шуга и снежура проникают через решетки окон и забивают решетки самотечных линий, на них, возможно, образуется и внутриводный лед. Летом 1965 г. решетки на раструбах самотечных линий были срезаны и в течение осени водозабор работал без них; закупорок не наблюдалось, зато шуга поступала в аванкамеры водоприемника и здесь забивала плоские сетки, особенно с размером ячеек 1´1 см. В практике водоснабжения используют различные мероприятия по борьбе с шуголедовыми помехами на водозаборах, которые можно рекомендовать для их ликвидации. Сложные вопросы защиты водозаборов от ледовых помех должны быть рассмотрены особо, после проведения дополнительных натурных наблюдений. ЛИТЕРАТУРА 1. Альтберг В.Я. Подводный лед. М.-Л., 1939. 2. Альтберг В.Я. Защита водозаборов от льда. М., Стройиздат, 1939. 3. Самочкин В.М. Ледотермический режим верхней Оби в естественном и регулируемом состоянии. Труды НИИЖТа, вып. XLIV. Новосибирск, 1965. 4. Дерюгин А.Г. К вопросу о ледовом режиме нижнего бьефа Нижне-Свирской ГЭС. Труды ГГИ, вып. 103, Л., 1963. 5. Нежиховский Р.А. Расчеты и прогнозы стока шуги и льда в период замерзания рек. Труды ГГИ, вып. 103. Л., 1963. 6. Макеров Н.С. Влияние водохранилища на работу водозабора в нижнем бьефе. Известия вузов. Серия «Строительство и архитектура», № 7, Новосибирск, 1964. 7. Кузуб Г.Я. Ковшовые водозаборы на реках Сибири. Труды НИИЖТ, вып. XXXVI. Новосибирск, 1963. 8. Готлиб Я.Л., Займин Е.Е., Раззоренов Ф.Ф., Цейтлин Б.С. Ледотермика Ангары. Л., 1964. 10. Образовский А.С. Гидравлика водоприемных ковшей. М., 1962. 11. Бибиков Д.Н., Петруничев Н.Н. Ледовые затруднения на гидростанциях. М., Госэнергоиздат, 1950. 12. Ергин В.П. Перемещение кромки ледостава в нижнем бьефе Новосибирской ГЭС. Труды ТЭИ СО АН СССР, вып. 15, Новосибирск, 1964. 13. Горюнов И.В. Испытание решеток на устойчивость против обмерзания. Журнал «Водоснабжение и санитарная техника» № 1, 1964. 14. Ховард Берг (Норвегия). Образование шуги в реках. Доклад на XI конгрессе МАГИ. Л., 1965. Инж. А.Е. ЯКУНИНРАСЧЕТ ЛЕДЯНОГО ПОКРОВА С УЧЕТОМ ИЗМЕНЕНИЯ МОДУЛЯ ДЕФОРМАЦИИ ПО ЕГО ТОЛЩИНЕВ настоящее время при расчете несущей способности ледяного покрова по теории изгиба пластинок модуль деформации Е и коэффициент Пуассона v принимают постоянными по его толщине независимо от строения и температуры отдельных слоев льда. Для этих условий дифференциальное уравнение изгиба ледяного покрова имеет вид где w - прогиб ледяного покрова; q (х, у) - нагрузка; k - постоянный коэффициент, равный объемному весу воды; D - цилиндрическая жесткость, находится но формуле
здесь h - толщина ледяного покрова. Однако экспериментами установлено, что значения Е и v в той или иной мере зависят от температуры льда, ориентации усилия относительно осей кристаллов и других факторов. Влияние температуры на величину Е изучалось рядом исследователей. В.Н. Пинегин [1] для речного льда при температуре -5,9°С получил значение Е, равное 1,2·104 кг/см2, а при температуре от -15 до -19°С в среднем 2,1·104 кг/см2. По данным П.А. Писарева [2], с понижением температуры от 0 до -20°С Е возрастает пропорционально от 2·104 до 4,3·104 кг/см2 (рис. 1). Увеличение значения Е пресного льда с понижением температуры отмечалось Б.П. Вейнбергом [3], Б.Д. Карташкиным [4] и другими авторами. Рис. 1. Изменение модуля деформации в зависимости от температуры: 1 - по данным П.А. Писарева для пресного льда; 2 - по данным А.М. Баталина для соленого льда Зависимость модуля деформации морского льда от температуры (см. рис. 1) изучалась А.М. Баталиным [5]. Для льда, имеющего соленость 5-6 ‰, он получил формулу для Е (в т/см2)
где θ - среднесуточная температура за период, непосредственно предшествовавший испытанию, взятая со знаком минус. Зависимость модуля деформации от ориентации кристаллов исследовал К.R. Koch [6]. Он установил, что модуль деформации озерного льда в направлении, параллельном оптическим осям кристаллов при температуре -8°С, на 10 % больше модуля деформации в направлении, перпендикулярном осям кристаллов. Примерно такие же результаты были получены И.П. Бутягиным [7]. Коэффициент Пуассона v также зависит от температуры и структурных свойств льда, но в незначительной степени. Поэтому при расчете ледяного покрова его величина может быть принята постоянной. Согласно определениям Б.Д. Карташкина [4] v в среднем равен 0,34, а Б.А. Савельева [8] - 0,36. Ледяной покров по своему температурному режиму и строению неоднороден. Его нижняя поверхность, соприкасающаяся с водой, имеет температуру, близкую к 0°С, температура верхней и средней частей зависит от температуры наружного воздуха, а также от толщины снеговых отложений. Верхние слои ледяного покрова вследствие влияния ледохода, ветра и течения имеют неправильное мелкокристаллическое строение, а нижние - шестоватую структуру [9]. При спокойном замерзании воды сначала образуются кристаллы, оптические оси которых преимущественно направлены параллельно поверхности замерзания. По мере нарастания ледяного покрова ориентация осей меняется. В озерном ледяном покрове [8] кристаллы с оптическими осями, параллельными поверхности замерзания, встречаются примерно на глубине 17 см, а ниже все кристаллы имеют оптические оси, перпендикулярные плоскости замерзания. Ледяной покров имеет включения воздуха и газов, которые неравномерно распределяются по его толщине. Кроме того, слои льда могут содержать и воду. В соответствии с температурой и строением отдельных слоев льда изменяется и модуль деформации (рис. 2).
Рис. 2. Эпюры изменения модуля деформации по толщине ледяного покрова в зависимости от температуры. Пунктиром показано изменение модуля деформации согласно теоретическим формулам. Распределение температуры принято по данным Г.Я. Кузуба [11], а зависимость Е от температуры - по рис. 1 Отсутствие экспериментальных данных не дает возможности построить эпюры изменения Е в зависимости от строения отдельных слоев ледяного покрова. Можно только указать, что в верхних слоях льда при спокойном замерзании воды модуль деформации будет несколько больше (приблизительно на 10 %), чем в нижних слоях. Таким образом, величина Е не постоянна по толщине ледяного покрова, а изменяется от точки к точке в зависимости от температуры и структурных свойств льда. С целью оценки влияния этого фактора на несущую способность ледяного покрова были произведены теоретические исследования, результаты которых изложены в данной статье. В общем случае ледяной покров можно рассматривать как трансверсально-изотропную пластинку с переменными Е и v по ее высоте. Физические уравнения для такой пластинки будут иметь вид:
где E, v - модуль деформации и коэффициент Пуассона в плоскостях, параллельных поверхности замерзания, являются функциями z; E', v' - модуль деформации и коэффициент Пуассона в плоскостях, перпендикулярных поверхности замерзания, также зависит от z. Однако расчет ледяного покрова при такой постановке вопроса представляет сложную задачу [16]. Поэтому введем допущения, которые принимаются в технической теории изгиба пластинок [17]: 1) совокупность точек, лежащих до деформации пластинки на какой-либо прямой; перпендикулярной к серединной плоскости, остается на прямой, нормальной к упругой поверхности деформированной пластинки, что равносильно предположению равенства нулю:
2) напряжения σz, возникающие вследствие взаимного нажима горизонтальных слоев друг на друга, не оказывают существенного влияния на σх , σy и τху, так что ими можно пренебречь. Кроме того, коэффициент Пуассона будем считать постоянным. При этих допущениях изгиб трансверсально-изотропного ледяного покрова сводится к изгибу изотропного ледяного покрова с переменным по высоте E, а уравнения (4), разрешенные относительно напряжений, будут иметь вид:
Связь между компонентами деформаций и прогибами w выражается формулами:
Подставляя значения εх, εу и γxy в (4а), получим:
При переменном Е нейтральный слой будет смещен относительно серединной плоскости. Его положение определится из равенства нулю усилий, действующих параллельно оси х или у по отношению где h1 и h2 - расстояния от нижней и верхней поверхностей ледяного покрова до нейтрального слоя (рис. 3).
Рис. 3. Расчетная схема ледяного покрова: 1 - срединная плоскость; 2 - нейтральный слой Изгибающие и крутящие моменты Мх, Му, Мху и Mуx., приходящиеся на единицу сечения, будут равны:
где
Подставляя значения Мх, Му и Мxy в уравнение равновесия элемента пластинки [15] и полагая р (х, y) = q(x, у) - kw, получим следующее дифференциальное уравнение:
Это уравнение по форме совпадает с уравнением (1), следовательно, для получения необходимых расчетных зависимостей можно воспользоваться решениями уравнения (1), подставляя в них значения D' вместо D. Таким образом, задача расчета ледяного покрова с учетом изменения Е по его толщине сводится к решению дифференциального уравнения (9), определению положения нейтрального слоя и жесткости по формулам (6) и (8). Для получения конкретных расчетных зависимостей необходимо располагать законом изменения модуля деформации по толщине ледяного покрова. Анализ экспериментальных данных показывает, что для зимнего периода, когда температура верхней поверхности ледяного покрова ниже температуры нижележащих слоев, этот закон может быть принят в следующем виде: где Е1 и Е2 - модули деформации соответственно нижней и верхней поверхностей ледяного покрова. Чтобы
определить коэффициент n,
требуется знать величину Е в
какой-нибудь промежуточной точке. Возьмем эту точку в серединной плоскости с координатой,
равной
Разрешая это уравнение относительно n, получим
Формула (10) дает удовлетворительные результаты при n ≥ 0,5, поэтому если по расчету n окажется меньше 0,5, то его следует принимать равным 0,5. Расстояние h1 до нейтрального слоя из условия (6) будет равно
Подставляя значение Е в формулу (8) и интегрируя, найдем следующее выражение для жесткости:
Зависимость (10) применима, если E2 > Eср > Е1 однако наблюдаются случаи, когда Е2 ≤ Еср > Е1, например в весенний период или при значительном повышении температуры зимой. Для этих условий изменение Е по толщине ледяного покрова может быть описано: 1) при значениях z от 0 до h1 2) при z от 0 до -h2
где Eн - модуль деформации нейтрального слоя; n1, n2 - целые числа больше единицы. Знак плюс в выражении (14) соответствует нечетному значению n2, а знак минус - четному. Нейтральный слой при изменении Е по формулам (13) и (14) смещается относительно серединной плоскости на небольшую величину, при этом разница между Eн и Еср получается незначительной. В целях упрощения расчетов можно принять Eн = Eср, тогда положение нейтрального слоя и жесткость будут определяться формулами:
При n1 = n2 = n и Е2 = Е1 модуль деформации изменяется симметрично относительно серединной плоскости. Жесткость в этом случае будет равна
Значения n1, n2 и n в практических расчетах можно принять равными соответственно 2, 3 и 2. Эпюры изменения Е согласно формулам (10) и (13), (14) даны на рис. 4. Принятые законы позволяют находить положение нейтрального слоя и вычислять жесткость ледяного покрова, если известны E1, Е2 и Eср. Для их определения необходимо иметь данные о температуре и строении соответствующих слоев ледяного покрова. В практических расчетах температура нижней поверхности ледяного покрова может быть принята равной 0°С, а верхней - в соответствии с температурой наружного воздуха. При наличии снега необходимо учитывать его теплоизоляционные свойства. Температура серединной плоскости принимается на основании экспериментальных данных, а при отсутствии последних может быть принята равной средней температуре ледяного покрова, которая согласно исследованиям Г.Я. Кузуба [11] находится на глубине (0,46 ÷ 0,54) h от верхней поверхности, т.е. весьма близко от серединной плоскости.
Pиc. 4. Теоретические эпюры изменения модуля деформации по толщине ледяного покрова Изменение модуля деформации согласно формулам (10) и (13), (14) дано на рис. 2 пунктирными линиями. Сравнение эпюр показывает, что принятые законы вполне удовлетворительно аппроксимируют опытные кривые. Чтобы дать количественную оценку влияния изменения модуля деформации на несущую способность ледяного покрова, рассмотрим две задачи. 1. Изгиб неограниченного ледяного покрова при действии нагрузки Р, равномерно распределенной по площади круга радиусом α. Уравнения прогибов, удовлетворяющие граничным условиям и дифференциальному уравнению (8), выраженному в цилиндрических координатах, будут иметь вид:
где q - интенсивность нагрузки; f1(ρ), f2(ρ), f3(ρ), f4(ρ) - цилиндрические функции. Свойства этих функций, а также их таблицы даны С.А. Бернштейном [12] и Б.Г. Кореневым [13], где они соответственно обозначены Z1(x), Z2(x), Z3(x), Z4(x) и u0(ξ), v0(ξ), f0(ξ), g0(ξ); В1, В2, B3 и В4 - постоянные интегрирования, имеющие следующие значения:
где
Подробный вывод уравнении (18) опубликован в [13], [11]. Напряжения в зоне распределения нагрузки могут быть представлены следующими формулами:
Под центром нагрузки σr и σθ равны и имеют максимальные значения:
Подставляя
значения В2, и
обозначив через получим
Напряжения в плоскости нижней поверхности ледяного покрова при z = h1 будут равны
В плоскости верхней поверхности при z = -h2
Экспериментами установлено, что разрушение ледяного покрова начинается с нижних слоев льда путем образования радиальных трещин, поэтому для определения нагрузки, способной вызвать эти трещины, необходимо исходить из формулы (21). Полагая, что σ1max = σи, где σи - предел прочности нижней поверхности ледяного покрова, получим следующую формулу:
Коэффициент В(α) зависит только от α, его значения находят по графику (рис. 5).
Рис. 5. График для определения коэффициента В(α) Для случая E = const формула (23) будет иметь вид
Если в ней принять h в метрах, σи - в т/м2, a B(α) выразить через С(α),.т.е. В(α) = 5С(α), то она будет совпадать с известной формулой С.А. Бернштейна [12]. Графики
изменения несущей способности речного и морского ледяного покрова в зависимости
от температуры согласно формулам (23) и (24) даны на рис. 6. Исходные данные
при вычислении нагрузок были приняты следующие: толщина ледяного покрова
Рис. 6. Изменение несущей способности бесконечного ледяного покрова в зависимости от температуры (σи - const, разрушение начинается с нижних слоев льда): а - ледяной покров из пресного льда; б - то же из соленого; в - температура верхней поверхности ледяного покрова; θcp - то же серединной плоскости Анализ
графиков показывает, что несущая способность ледяного покрова при E = φ(z) с понижением температуры верхней поверхности θ1 и срединной плоскости
θcp возрастает, а при E = const
уменьшается.
Максимальные расхождения в величинах нагрузки составляют: при θ1 = Полученные результаты относятся к случаю, когда ледяной покров разрушается с нижних слоев льда; однако при определенных условиях он может разрушаться и с верхних слоев. В связи с этим рассмотрим вторую задачу. 2. Изгиб
полубесконечного ледяного покрова при действии нагрузки интенсивностью q,
приложенной к его кромке. Для получения расчетных зависимостей в этом случае
достаточно рассмотреть полоску шириной
где C - постоянная интегрирования, равная при
Напряжения определятся формулой
Максимальные σ возникают в сечении при х = π/4β и будут равны
Подставляя
значения С, β и
Напряжения в нижней поверхности при z = h1 будут
В верхней при z = -h2
При данной схеме загружения ледяного покрова его разрушение начинается с верхних слоев льда, поэтому для нахождения предельной нагрузки следует исходить из формулы (28). Полагая в ней σ2max = σи, где σи -предел прочности льда верхней поверхности ледяного покрова, получим формулу
При E = const формула будет иметь вид
Изменения несущей способности ледяного покрова в зависимости от температуры согласно формулам (29) и (30) показаны на рис. 7.
Рис. 7. Изменение несущей способности полубесконечного ледяного покрова в зависимости от температуры (σи - const, разрушение начинается с верхних слоев льда): а - ледяной покров из пресного льда; б - то же из соленого; θ1 - температура верхней поверхности ледяного покрова, θcp - то же серединной плоскости Исходные данные приняты те же, что и в предыдущем случае, в том числе и предел прочности льда, поскольку его величина при оценке влияния Е на несущую способность ледяного покрова не играет роли. Анализ
графиков показывает, что несущая способность ледяного покрова с понижением
температуры θ1 как в
случае E = φ(z), так и в случае Е = const уменьшается. Однако
степень изменения различна. Так, с понижением θ1 от 0 до -20°С при θcp = -15°С несущая
способность ледяного покрова из пресного льда с переменным Е уменьшилась на 66 %, из соленого
льда - на 94 %, а при E
= const - соответственно только па 7 и 8 %. Далее с
понижением θcp
несущая способность при E
= φ(z)
возрастает,
а при E = const
уменьшается.
Максимальные расхождения в величинах нагрузки составляют: при θ1 = Таким образом, предельная нагрузка, действующая на ледяной покров, существенно зависит от характера изменения Е по его толщине. В случае когда разрушение происходит с нижних слоев льда, нагрузка при E = φ(z) получается больше, чем при E = const, а в случае разрушения с верхних слоев льда она или больше, или меньше. Поэтому ледяной покров при оценке его несущей способности необходимо рассчитывать с учетом изменения модуля деформации по его толщине. В связи с этим требуется детальное изучение зависимости величины Е от температуры и структурных свойств льда, а также более подробное исследование строения и температурного режима ледяного покрова. ЛИТЕРАТУРА 1. Пинегин В.Н. Предварительные сообщения об исследованиях прочности речного льда в связи с температурными изменениями. Вестник сибирских инженеров, т. IV, № 5, Томск, 1923. 2. Писарев П.А. Работа льда на изгиб. Диссертация, 1944. 3. Вейнберг Б.П. Лед. Гостехиздат, М.-Л., 1940. 5. Песчанский И.С. Ледоведение и ледотехника. Изд-во «Морской транспорт», Л., 1963. 6. Koch К.R. Uber die Elastizität der Eises Ann der Physik, Leipzig B. 41, 1913 (709-727), B. 45, 1914 (237-258). 7. Бутягин И.П. Прочность ледяного покрова. Изд-во «Наука», Сибирское отд., Новосибирск, 1966 10. Войтковский К.Ф. Механические свойства льда. М, Изд-во Академии наук, 1960 12. Бернштейн С.А. Ледяные переправы. XVIII сборник отдела инженерных исследований Научно-технического комитета НКПС, М., 1929. 13. Коренев Б.Г. Вопросы расчета балок и плит на упругом основании. М , 1954. 14. Scheicher F. Kreisplatten auf eiosticher 15. Тимошенко С. П. Пластинки и оболочки. М., Физматгиз, 1963. Проф. К.Н. КОРЖАВИН, инж. Ф.И. ПТУХИНВЛИЯНИЕ СКОРОСТИ НАГРУЖЕНИЯ НА ОЦЕНКУ ПРОЧНОСТИ ЛЬДА В РАСЧЕТАХ ЛЕДОВЫХ НАГРУЗОКСтроительство крупных гидротехнических и транспортных сооружений различного назначения в районах с длительным зимним периодом часто вызывает необходимость определения ледовых нагрузок, действующих на сооружения во время весенних ледоходов. Это требует знания механических свойств ледяного покрова и их изменения в зависимости от различных факторов. В частности, одним из наиболее существенных показателей механических свойств ледяного покрова, определяющих величину возможных нагрузок на сооружения, является его предел прочности. Ныне действующие технические условия определения ледовых нагрузок на речные сооружения (СН 76-59) рекомендуют вполне определенные расчетные величины прочности льда. Имеются такие данные и в проекте новых норм. Однако как действующие, так и разрабатываемые нормы рекомендуют для ответственных сооружений уточнять величины расчетной прочности ледяного покрова непосредственными экспериментальными измерениями с учетом конкретных условий предполагаемого района строительства. Эти уточнения неизбежны для районов Заполярья и низовьев сибирских рек, в связи с чем большое значение приобретают вопросы разработки методики объективной оценки пределов прочности льда по испытаниям его образцов с учетом факторов, непосредственно связанных со способом экспериментального определения прочности. Известно по данным экспериментальных определений, что наряду с другими факторами на оценку прочности льда оказывает существенное влияние скорость деформирования или нагружения испытуемых образцов ледяного покрова. При переменных напряжениях, быстро растущих до значений предела прочности, скорость деформирования и продолжительность действия нагрузки в большой степени будут определяться скоростью возрастания напряжений. Вследствие этого как изменение скорости деформирования, так и скорости нагружения должно качественно одинаково влиять на изменение прочности. Очевидно, поэтому в равной мере часто оба эти показателя рассматриваются в качестве характеристики скоростного режима нагружения. При разрушении образцов льда с достаточно высокими значениями названных показателей скоростного режима нагружения рядом авторов [1-5] были получены противоречивые результаты. В одних случаях было отмечено увеличение предела прочности с возрастанием величин показателей скоростного режима нагружения образца, в других - предел прочности, наоборот, становился меньше. Независимо от характера изменения прочности льда влияние скорости нагружения существенно сказывается в диапазоне скоростей нагружения при испытаниях образцов на различных испытательных машинах. Поэтому учет влияния скорости нагружения, особенно имея в виду отсутствие стандартной методики испытаний, регламентирующей скоростной режим, имеет важное значение как для объективной оценки прочности льда по данным разрушения образцов на испытательных машинах, так и для разработки стандартной методики таких испытаний. Последнее значительно облегчило бы теоретическое обобщение данных многих исследователей и выбор расчетных значений прочности льда на его основе. Выяснение причин получения противоречивых результатов при исследовании влияния на прочность льда рассматриваемых факторов требует детального анализа условий экспериментирования. Это не всегда можно сделать по данным публикаций из-за отсутствия подробного описания методики опытов. Во всяком случае можно полагать, что различие результатов объясняется прежде всего существенно отличными скоростями нагружения. При относительно малых скоростях нагружения лед ведет себя как большинство упруго-вязких тел, и если скорость его нагружения не превышает некоторого предела, прочность возрастает с увеличением скорости нагружения. Этот вывод подтверждается [1] и хорошо иллюстрируется [3] графиками (рис. 1), на которых нетрудно видеть, что превышение некоторого «критического» значения скорости нагружения ведет к уменьшению предела прочности с увеличением скорости нагружения. Рис. 1. Зависимость предела прочности на сжатие от скорости нагружения для погребенного льда естественной структуры по данным Л.С. Хомичевской: 1 - при температуре -10°С; 2 - то же 5°С; 3 - то же 2,5°С; 4 - то же 0°С В свое время были выполнены опыты [4, 5] по установлению зависимости предела прочности льда на сжатие от скорости деформирования, причем в исследованном диапазоне скоростей деформирования, которые определялись исходя из скорости хода подвижной траверсы испытательной машины, было получено уменьшение величины предела прочности с увеличением скорости деформирования. Следует оговориться, что дальнейшие исследования показали условность определения скорости деформирования исходя из скорости холостого хода подвижной траверсы пресса, поскольку оно выполняется без учета изменения скорости ее движения, связанного с соотношением жесткостей испытательной машины и деформируемого образца. Как показало осциллографирование процесса нагружения, скорость деформирования, оставаясь постоянной вплоть до разрушения образца, существенно отличается по величине от скорости, в основу определения которой положена величина скорости холостого хода траверсы пресса. Поэтому данные, полученные в зависимости от условных скоростей деформирования, пригодны лишь для сопоставления результатов опытов, полученных на машинах с примерно одинаковыми рабочими характеристиками. В дальнейшем нами были выполнены исследования изменения прочности льда в зависимости от скорости нагружения. Использование этого показателя в качестве скоростной характеристики режима нагружения имеет некоторые методические преимущества перед скоростью деформирования. Во-первых, фиксировать скорости нагружения образцов при работе с осциллографом можно проще и с меньшими искажениями, чем искажения скорости деформирования. Во-вторых, при определении фактического давления ледяных полей на сооружения (опоры мостов или другие) скорость изменения нагрузки, а следовательно, и напряжений легко может быть зафиксирована осциллографированием при монтаже датчиков на динамометрических плитах типа предложенных В.К. Моргуновым [6]. Непосредственное же измерение скорости деформирования ледяного поля при взаимодействии его с сооружением практически невыполнимо. Измерение фактического давления на сооружение с записью изменения нагрузки во времени на осциллограф была бы весьма полезно. Результаты таких исследований позволили бы сопоставить данные лабораторных и натурных наблюдений и дали бы экспериментальный материал для разработки зависимостей для пересчета данных от лабораторных к натурным условиям и уточнения зависимости прочности льда от скорости нагружения в области весьма высоких скоростей нагружения. В настоящее же время для рассмотрения противоречий, существующих по данному вопросу, вынужденно пользуемся результатами преимущественно лабораторных исследований. Причина существования двух отмеченных видов зависимости прочности льда от скорости нагружения, по-видимому, кроется в особенности внутренних процессов деформирования и перераспределения внутренних напряжений между компонентами материала, т.е. между отдельными его «зернами», имеющими различные реологические свойства. В случае приложения нагрузки распределение внутренних напряжений в ледяном поле будет следовать не только закону поля напряжений, созданному внешней нагрузкой. В силу различия свойств смежных «зерен» величина напряжений в каждом элементарном объеме материала будет отклоняться от рассчитанной в предположении его идеальной однородности и сплошности. Кроме того, это должно усугубляться наличием различного рода посторонних включений и нарушений строения ледяного тела (минеральные частицы, трещины и т.п.), которые служат концентраторами напряжений. Неравномерность распределения внутренних напряжений, вызываемая перечисленными факторами, не может оставаться постоянной во времени в силу протекания внутренних процессов в нагружаемом теле [1, 7]. Снижение предела прочности льда с увеличением скорости нагружения не противоречит тому представлению о механизме деформирования поликристаллического льда, которое дается К.Ф. Войтковским [7]. Согласно этому представлению процесс деформирования состоит из двух противоположных процессов: нарушения внутренних связей и расслабления ледяного тела; восстановления этих связей и упрочнения. Если напряжения не ведут к нарушению сплошности образца и процесс деформирования достаточно длителен (малые скорости нагружения), то наряду с нарушением связей происходит восстановление их, залечивание нарушений. В результате местных внутри- и межкристаллических сдвигов и скольжений напряжения в перенапряженных точках релаксируют, уменьшаются местные градиенты напряжений. При больших скоростях возрастания напряжений из-за недостатка времени для выравнивания внутренних напряжений неоднородность их распределения будет возрастать. Будут расти местные напряжения и градиенты напряжений в элементарных объемах материала, что в результате должно повести к быстрому накоплению нарушений в слабых и перенапряженных местах образца. Равновесие процессов нарушения и восстановления связей будет нарушено, образец разрушится. При этом среднее разрушающее напряжение, определенное для единицы площади сечения образца, может быть тем меньшим, чем быстрее возрастает неоднородность распределения внутренних напряжений и чем быстрее растут местные градиенты напряжений. Весь процесс носит деформационно-релаксационный характер. С целью феноменологического описания поведения тела под нагрузкой во времени его свойства обычно аппроксимируются свойствами соответствующей реологической модели [8, 9]. Это приводит к большей или меньшей идеализации как самого тела, так и его свойств, но дает возможность получить математические зависимости между напряжениями и деформациями, а также скоростями их изменения, которые позволяют проанализировать поведение тела при различных скоростях режима нагружения. Лед обычно относится к категории упруго-вязких тел и свойства его аппроксимируются свойствами реологических моделей, усложняющихся по мере необходимости описать возможно большее число особенностей деформирования (начальная упругая стадия, неустановившаяся ползучесть, последействие при разгрузке и т.д.). Из рассматривавшихся реологических моделей льда наиболее проста модель тела Максвелла и наиболее сложна модель, состоящая из последовательно соединенных реологических тел Максвелла и Кальвина (Фойхта) [10]. Последняя модель, поведение которой под нагрузкой описывается линейным дифференциальным уравнением второго порядка, очевидно, в качественном отношении наилучшим образом отвечает поведению льда под нагрузкой. Однако с целью качественного воспроизведения закономерностей изменения прочности в зависимости от скорости нагружения удобно принять модель (см. ниже рис. 3), состоящую из параллельно работающих чисто упругого элемента (с малым модулем упругости) и тела Шведова (Бингама). Она в достаточной мере качественно хорошо воспроизводит особенности деформирования льда. При определенных предположениях об условиях ее прочности эта модель дает возможность показать, что изменение прочности с изменением скорости нагружения будет иметь особенности, отмеченные при экспериментальном исследовании льда. Связь между действующими напряжениями, деформациями и скоростями их изменения для предлагаемой модели может быть выражена дифференциальным уравнением
где Е - длительный модуль упругости; Е1 + Е = Н - мгновенный модуль упругости; n - период релаксации напряжений; σ - напряжение в модели;
ε - относительная деформация модели;
σт - напряжение в элементе модели, имитирующее внутреннее сухое трение, по достижении которого начинается развитие вязкой деформации.
Рис 2 Осциллограмма деформирования образца ледяного покрова при сжатии: 1 - нагрузка Р = f(t); 2 - деформация ∆l = f2(t) Уравнение (1) может быть решено для различных условий нагружения [8, 9] как относительно σ, так и относительно ε. В приложении к рассматриваемому вопросу прежде всего представляет интерес решение приведенного уравнения при условии постоянной скорости нагружения. Такие режимы нагружения проведены при испытаниях образцов льда (рис. 2) В этом случае решение уравнения (1) в конечном итоге дает следующее выражение для связи между деформацией, скоростью и продолжительностью нагружения:
где εт - деформация модели, обеспечивающая достижение величины σт. В уравнении
(2) деформация Рис. 3. Теоретический график изменения прочности реологической модели льда и зависимости от скорости нагружения и схемы реологической модели В классической теории сопротивления материалов для идеально однородного тела условия прочности в соответствии с различными гипотезами могут быть выражены одним из следующих соотношений:
В случае если материал и его свойства представлены реологической моделью типа принятой, естественно предположить, что прочность модели в целом будет зависеть от прочности отдельных ее элементов. Условия же прочности каждого из элементов модели могут быть записаны аналогично одному из приведенных выше. В состав модели входят элементы, свойства которых зависят от продолжительности нагружения и скорости изменения напряжений, что отражено в математических выражениях. В процессе нагружения такой модели в зависимости от длительности действия или скорости приложения нагрузки будет происходить перераспределение напряжений между отдельными элементами модели. В связи с этим достижение предельных деформаций или напряжений в том или ином элементе модели, а следовательно, ее прочность в целом будут определяться скоростью нагружения. Обычно различают хрупкое и вязкое разрушение материала. Хрупкое разрушение происходит, как правило, при незначительных по величине деформациях с мгновенным разделением образца на части. Вязкое же разрушение, наоборот, предполагает большие деформации и зачастую потерю образцом способности сопротивляться нагрузке еще до разделения на части. Следовательно, для того чтобы проанализировать возможное изменение прочности принятой модели в зависимости от скорости нагружения, следует задаться частными условиями прочности отдельных элементов модели. Этими условиями могут быть:
Первое из
записанных условий прочности представляет собой как условие мгновенной
прочности модели в том случае, если мгновенно приложенное напряжение вызывает
деформацию Второе условие прочности обусловливает как длительную прочность модели при постоянных напряжениях, меньших мгновенной прочности, так и при напряжении, возрастающем с постоянной скоростью, меньшей «критической». Следует отметить, что наряду со вторым условием прочности может быть записано еще одно условие прочности в виде
Это третье условие прочности аналогично второму с той лишь разницей, что второе предполагает переменную полную предельную деформацию, зависящую от скорости нагружения, в то время как третье приводит к независимости полной предельной деформации от режима нагружения при сохранении такой зависимости для прочности. Кроме
указанных условий, предполагается, что предельная деформация при соблюдении
двух последних условий прочности должна превышать по величине предельную
деформацию при соблюдении первого условия прочности, иначе
Напряжение в упруго-вязкой части модели
Выражая деформации элементов модели через действующие в них напряжения и используя первое условие прочности, в результате необходимых преобразований получим формулу для прочности модели
Эта формула непосредственно связывает прочность модели со скоростью ее нагружения и имеет смысл в пределах изменения скорости нагружения от любого значения первое условие прочности утрачивает свое значение. Характер разрушения должен изменяться от хрупкого к вязкому и прочность будет определяться вторым условием прочности.
При использовании второго условия прочности в результате соответствующих выкладок получим уравнение
Это уравнение не дает возможности выразить прочность модели непосредственно через скорость нагружения, его удобно решить графически. В результате выполненных вычислений при заданных показателях реологических свойств модели получен график изменения прочности модели зависимости от скорости нагружения (см. рис. 3), причем правая ветвь графика построена по формуле (6), левая же отвечает уравнению (7). Нетрудно видеть, что изменение прочности предлагаемой модели качественно отвечает экспериментальным результатам, представленным ранее графиками (см. рис. 1). Таким образом, в известной мере объясняется существующее противоречие в полученных различными исследователями экспериментальных результатах. По-видимому, предлагаемое решение окажется полезным для разработки методических положений дальнейших исследований: вопроса и для получения более простых расчетных приемов оценки влияния скорости нагружения на прочность льда, особенно в диапазоне скоростей, отвечающих правой ветви полученного графика (см. рис. 3). Вследствие
характера проводимых исследований нет возможности привести экспериментальные
результаты, отвечающие левой ветви кривой σr = f( Остановимся коротко на некоторых условиях проведения опытов. При испытании образцов фиксировали следующие показатели: - скорость нагружения на основании данных осциллографирования; - величину разрушающей нагрузки; - температуру образца в момент опыта; - продолжительность нагружения до момента разрушения образца. Все опыты проводили на образцах льда, строение которого не подвергалось значительным изменениям в процессе таяния. При этом подбирали одинаковые по наличию видимых особенностей строения группы образцов, чтобы по возможности уменьшить их влияние на результаты опытов в различных скоростных режимах нагружения. Испытывали в лабораторных помещениях при положительных температурах воздуха, а образцы перед опытом выдерживали в оборудованном контейнере, где с помощью ледосоляной смеси поддерживался необходимый термический режим. Температуру льда контролировали с помощью термопар, вмороженных в контрольные образцы. Измерения показали, что температура образцов льда во время испытания мало отличалась в отдельных образцах и ее колебания не могли повлиять на результаты определения прочности в различных скоростных режимах нагружения.
Приведенные в таблице результаты опытов ясно свидетельствуют о снижении предела прочности образцов льда с повышением скорости нагружения. Характер кривой изменения прочности (рис. 4) качественно отвечает характеру правой ветви теоретической кривой; это позволяет надеяться, что при накоплении большего количества экспериментальных данных можно определить необходимые параметры теоретических зависимостей для льда.
Рис 4. Зависимость предела прочности льда на сжатие от скорости нагружения При оценке предела прочности льда по данным кратковременных испытаний образцов на стандартных испытательных машинах, безусловно, следует учитывать скоростной режим их нагружения. Нагружение при опытах было скоростным, но все же статическим, т.е. не имело характера ударного нагружения. Имея в виду асимптотический характер зависимостей между прочностью и скоростью нагружения, можно предполагать, что в диапазоне ударных скоростей нагружения они не будут уже оказывать существенного влияния на оценку прочности. Однако это предположение требует экспериментального подтверждения путем уже упоминавшихся динамометрических измерений давления льда на сооружения с осциллографированием его изменения во времени. Для определения динамических нагрузок впредь до проведения таких исследований расчетную прочность льда следует принимать по данным испытаний образцов с возможно высокими скоростями нагружения. ЛИТЕРАТУРА 2. Цытович Н.А, Сумгин М.И. Основания механики мерзлых шунтов. М., изд-во АН СССР, 1937. 4. Коржавин К.Н. Воздействие льда на инженерные сооружения. Изд-во СО АН СССР. Новосибирск, 1962. 7. Войтковский К.Ф. Механические свойства льда. М , изд-во АН СССР, 1960. 8. Рейнер М. Реология. М., изд-во «Наука», 1965. Канд. техн. наук У.С. РОСЬИЗМЕНЕНИЕ ПРИВЕДЕННОГО КОЭФФИЦИЕНТА ШЕРОХОВАТОСТИ В ЗАВИСИМОСТИ ОТ ГЛУБИНЫ ПОТОКА ПОД ЛЕДЯНЫМ ПОКРОВОМВ гидравлике открытых русел под профилем скоростей по вертикали понимают график изменения продольных осредненных скоростей в функции от координаты у. Направление этой координатной оси выбирается обычно вертикальным от дна к свободной поверхности. В свое время Базен и Бахметев опытами установили, что максимальная скорость находится на поверхности открытого потока при отношении ширины его к наполнению b/h ≥ 5. Из опытов В.Н. Гончарова следует, что даже при b/h = 10 максимальная скорость находится ниже свободной поверхности. Поэтому рекомендация считать поток плоским при определенных значениях b/h зависит в основном от той точности, которая обеспечена при определении пропускной способности лотков. Безусловно, влияние боковых стенок на распределение скоростей по вертикали проявляется при самых различных отношениях b/h. При большем наполнении лотка это влияние распространяется на большее расстояние от стенок. Подобное влияние оказывает и шероховатость боковых стенок: чем больше коэффициент шероховатости стенок, тем сильнее проявляется их влияние (рис. 1).
Рис. 1. Изотахи дна лотка: а - со стеклянными стенками, б - с шероховатыми стенками из керамзитовых шариков Теперь представим себе, что периметр лотка имеет неоднородную шероховатость. Это могут быть потоки под ледяным покровом, где коэффициент шероховатости ледяного покрова и русла потока неодинаков. В этом случае на протекание потока влияние периметров с различной шероховатостью будет проявляться с неодинаковой силой. Поэтому приведенный коэффициент шероховатости nпр таких русел будет зависеть от соотношения периметров с различной шероховатостью, а для прямоугольных потоков - в конечном итоге от глубины наполнения. Как показали опыты, зависимость эта имеет сложный характер. Опыты проводили для исследования некоторых вопросов гидравлики потока под ледяным покровом. Для исследования этого вопроса необходимо обоснованно выбрать расчетную схему. Возможны две схемы: - ледяной покров не связан с берегами, т.е. свободно плавает на поверхности и следует за колебаниями горизонта воды; - при известных условиях ледяной покров может смерзаться с берегами. В
большинстве случаев более обоснована первая схема. Известно, что сцепление с
берегами зависит от местных особенностей и их характера. В то же время, как
показали наблюдения В.Н. Гончарова [1]
и других авторов, сила сцепления льда с берегами относительно мала. Например,
при быстром увеличении глубины всего на В процессе проведения опытов соотношение шероховатостей ледяного покрова и русла меняли в пределах 0,5-2,37, что наиболее часто встречается в натурных данных. Методика определения опытов и схема установки известны [2]. Опыты проведены в квадратичной области турбулентной зоны. На основании опытных данных показано изменение nпр (рис. 2) от глубины равномерного режима для нескольких серий опытов, выполненных при определенных значениях nл/nпр.
Рис. 2. Зависимость nпр от глубины потока в лотке: V-XII - номера серий опытов Поскольку не ставили цели определения истинной величины nпр, а лишь на основании опытов устанавливали характер зависимости nпр в потоках под ледяным покровом при изменении глубины наполнения, то значения коэффициентов nпр, nл и nр подсчитывали по формуле Маннинга, хотя в течение последних лет появился ряд новых формул для коэффициента Шези. На графиках изменения nпр вертикальной линией отделены друг от друга две области, имеющие различный характер. Первая область на рис. 2 находится слева от вертикальной линии, а на рис. 3 эта же область находится справа от вертикальной линии. Большинство точек этой области получено путем экстраполяции. Первая область характеризуется тем, что для всех серий опытов кривые имеют одинаковую тенденцию, а именно: значение nпр увеличивается с увеличением глубины равномерного режима, или, что то же самое, с уменьшением соотношения χл/χр.
Рис. 3. Зависимость nпр от соотношения периметров χл/χр: V-XII - номера серий опытов Увеличение
приведенного коэффициента шероховатости следует отнести за счет потерь,
происходящих в результате образования вихрей и усиленной турбулентности в потоке.
Возрастание коэффициента шероховатости за счет вихревых возмущений происходит
до определенной глубины. Дальнейшее увеличение глубины приведет к тому, что
слой воды в лотке будет настолько велик, что вихревые движения у боковых стенок
сблизятся до соприкосновения друг с другом, поэтому они уже не окажут столь
значительного влияния на увеличение приведенного коэффициента шероховатости.
Такое явление ранее было подмечено [3,
4].
По этой причине значение приведенного коэффициента шероховатости возрастает до глубины h = Во второй области (справа от вертикальной линии на рис. 2 и слева на рис. 3) зависимость приведенного коэффициента шероховатости от наполнения лотка довольно сложная. Для некоторых серий опытов увеличение наполнения лотка приводит к увеличению nпр, а для других к уменьшению значения nпр. В этой области на изменении nпр, видимо, начинает сказываться соотношение периметров χл/χр , имеющих различную шероховатость. Другими словами, удельное влияние периметра лотка с увеличением глубины превышает влияние периметра ледяного покрова. Так, для опытов серий V, VI и IX во второй области увеличение глубины в лотке приводит к уменьшению nпр. В этом случае коэффициент шероховатости щитов больше, чем у лотка, поэтому увеличение глубины наполнения ведет к увеличению периметра с меньшим коэффициентом шероховатости. Для опытов серий VIII, X, для которых nл/nпр < 1, увеличение глубины потока способствует дальнейшему увеличению коэффициента nпр. Здесь опять проявляется удельное влияние периметра лотка, коэффициент шероховатости которого больше, чем у ледяного покрова. Для опытов серий XI и XII влияние боковых стенок с увеличением глубины в лотке проявляется значительно слабее, так как коэффициент шероховатости дна и стенок лотка очень мал (стеклянный лоток). Поэтому при тех расходах, а следовательно, и глубинах потока, которые были охвачены опытами, приведенный коэффициент шероховатости, хотя и незначительно, но увеличивается. И только при расходах Q = 60÷65 л/сек начинает проявляться влияние периметра лотка, которое можно уловить при глубинах, соответствующих указанным расходам. Таким образом, тенденция изменения приведенного коэффициента шероховатости при изменении глубины равномерного режима зависит от соотношения коэффициентов шероховатости nл/nпр. При nл/nпр < 1 значение nпр уменьшается с увеличением глубины, при nл/nпр > 1 значение nпр увеличивается с увеличением глубины. Однако изменения эти ограничены. Как бы ни изменялось значение nпр, всегда наблюдается: при nл/nпр > 1 nпр > nр; при nл/nпр < 1 nпр < nр. Следовательно, изменение приведенного коэффициента шероховатости в зависимости от глубины равномерного режима объясняется удельным влиянием периметров с различной шероховатостью. Это явление было подмечено [5] для открытых потоков с неоднородной шероховатостью. Итак, установлено, что nпр находится в сложной зависимости от соотношения периметров с различной шероховатостью, а для прямоугольных русел в конечном счете от глубины потока. Однако в настоящее время существует ряд формул, рекомендуемых для определения nпр в потоках под ледяным покровом [2]. Эти формулы в основном были получены из условия широкого прямоугольного русла. Только формула А.А. Сабанеева [2] рекомендуется для расчета русел любой формы. Чтобы убедиться, насколько эти формулы отражают тенденцию изменения nпр в зависимости от глубины потока, сопоставим их с опытными данными (рис. 4 и 5).
Так
как опытная установка позволяла менять глубины наполнения в диапазоне от 7 до Анализ существующих зависимостей показал, что наиболее близко совпадают с опытными данными формулы средневзвешенной шероховатости и А.А. Сабанеева для русел любой формы. Их расхождение с опытными данными не превышает 12 %. Эти формулы отвечают общей закономерности изменения nпр в зависимости от глубины потока при различных отношениях nл/nр. Общая формула хотя дает незначительные отклонения (до 20 %) от опытных данных, но не отражает общей закономерности изменения nпр от глубины потока. Она удовлетворительно согласуется [1] с опытными и натурными данными для широких русел, где можно принимать R = h/2. На графиках (см. рис. 4 и 5) не приведена формула П.Н. Белоконя, так как она дает значительные отклонения (до 10 %) от опытов. Формула же Лоттера не отражает общей тенденции изменения nпр при увеличении глубины для различных значений nл/nр. Таким образом, на основании опытных данных для потоков конечной ширины можно рекомендовать формулу средневзвешенной шероховатости и формулу А.А. Сабанеева при определении значений nпр. ЛИТЕРАТУРА 1. Гончаров В.Н. Наблюдения над зимним режимом южных рек. Вестник ирригации» № 1, 1928. 3. Пикалов Ф.И. Быстротоки с искусственной шероховатостью. Труды ВНИИГим, т. XIII, 1935. 4. Фалькович А.Я. Быстротоки с ботовой и комбинированной шероховатостью. Труды ВНИИГим, т. XIII, 1935. Канд. техн. наук И.К. ПОКЛОНСКИЙПРИМЕНЕНИЕ ПОВЫШЕННОЙ ШЕРОХОВАТОСТИ В ОТВОДЯЩИХ РУСЛАХ МАЛЫХ ИСКУССТВЕННЫХ СООРУЖЕНИЙОпределение типа и размеров укреплений отводящих русел, предназначенных для защиты мостов или труб от размыва, - одна из важных задач проектирования малых искусственных сооружений. При этом общей тенденцией является применение пассивного способа защиты, состоящего в том, что укрепление дается такой длины, при которой за ним уже не могут возникнуть опасные размывы. Так, по
разработанным в Однако в
случае устройства укрепления в отводящем русле, сложенном из несвязаных грунтов
(песок, мелкий гравий) глинистых (связных) грунтов, глубина размыва за
рисбермой, не исключена и по расчетным данным может достигнуть Размывающая способность потока в отводящем русле за гидравлическим прыжком определяется степенью шероховатости укрепления. Если сравнить размывающую способность потока [1] при различной шероховатости русла: 0,014 и 0,03, то окажется, что в случае бетонного русла интенсивная размывающая способность сохраняется на значительном участке и прекращается при длине его l = 20hбыт, где hбыт - бытовая глубина в отводящем русле. При шероховатом отводящем русле (n = 0,03 - каменное мощение) интенсивность размыва резко снижается и всякий размыв прекращается при l = 8hбыт. Следовательно, для уменьшения размывающей способности потока в отводящем русле и уменьшения размеров типовых укреплений, устраиваемых из железобетонных плит, целесообразна повышенная шероховатость. В частности, в некоторых проектах труб Сибгипротранса уже предусмотрена такая искусственная шероховатость. В гидравлической лаборатории НИИЖТа в содружестве с отделом мостов Сибгипротранса были проведены экспериментальные исследования условий протекания потока в отводящих руслах. Модель
искусственного сооружения была установлена в лотке шириной При проведении опытов трубкой Пито-Ребока измеряли скорости в различных сечениях: на выходе потока из сооружения, в сечении максимальной ширины растекания потока в отводящем русле и других характерных сечениях. Для определения глубин в этих сечениях измеряли отметки свободной поверхности потока и дна лотка. Вначале исследовали протекание потока в гладком отводящем русле (дно и стенки лотка стеклянные), потом в русле с повышенной шероховатостью (из брусков) и при одинаковых расходах проводили соответствующие измерения. Это давало возможность устанавливать эффективность гашения скорости потока при конкретном типе шероховатости. Протекание
потока в отводящем русле с повышенной шероховатостью за водопропускной трубой
прямоугольного сечения. Модель прямоугольной трубы отверстием Рис. 1. Схема модели трубы и отводящего русла с повышенной шероховатостью (первый вариант - бруски 6×8 мм): 1-4 - продольный разрез модели с укреплением участков русла разной длины (lш ) Рис. 2. Схема модели трубы и отводящего русла с повышенной шероховатостью (второй вариант - бруски 8×12 мм): 1-4 - см. рис. 1 Кроме того, для сравнения эффективности гашения энергии при том или ином типе шероховатости измеряли параметры потока в гладком отводящем русле модели трубы (повышенная шероховатость отсутствовала). Основные параметры потока определяли во всех опытах данной серии при трех расходах: 12,3; 19,8 и 28,3 л/сек. Протекание потока в отводящем русле было свободным, т. е. без подтопления со стороны нижнего бьефа. Эффективность гашения энергии в отводящем русле трубы, но дну которого создана повышенная шероховатость брусками сечением 6×8 мм, иллюстрируется на рис. 3. Точки 1-4 кривой I дают среднее значение скорости потока соответственно 1-4 участков, показанных на рис. 1; точки 1'-4' - среднюю величину скорости в тех же сечениях участков, но при гладкой поверхности русла, т. е. при отсутствии брусков шероховатости. Кривая II (см. рис. 3) характеризует изменение средней скорости от сечения полного растекания в отводящем русле и далее по длине потока, протекающего за сооружением в гладком отводящем русле. Здесь средняя величина скорости изменяется очень плавно, так как поток на этом участке протекает в бурном состоянии, причем глубины изменяются очень незначительно. Установка брусков шероховатости (см. рис. 1) приводит к резкому изменению картины протекания потока: скорости уменьшаются, глубины возрастают. Это видно на кривой I (см. рис. 3), характеризующей величины средней скорости по сечениям, измеренным в потоке при том же расходе, что и для кривой II, но при наличии шероховатости в отводящем русле.
Рис. 3. Эффективность гашения скоростей в отводящем русле с помощью искусственной шероховатости (Q = 12,3 л/сек) В
частности, при длине участка с повышенной шероховатостью lш =
Рис. 4. Эффективность гашения энергии при различных расходах Сравнивая данные на рис. 3 и 4 для одного и того же расхода (12,3 л/се/с), видим, что отличительная особенность данных этих двух графиков - различное сечение брусков шероховатости (6×8 и 8×12 мм), длина их и расстояние, на котором они устанавливались. Несмотря на то, что сечение брусков шероховатости больше, эффект гашения скорости в первом случае оказывается ниже. Это свидетельствует о том, что увеличение расстояния между отдельными брусками и их рядами (см. рис. 4) привело к снижению эффекта гашения скорости. Протекание потока в отводящем русле с повышенной шероховатостью за мостом. Модель имела необтекаемые конусы и поперечное трапецеидальное сечение русла в пределах моста. В отводящем
русле обеспечивали повышенную шероховатость прямоугольными брусками сечением
6×8 и 8×12 мм, длиной
В отводящем
русле бруски устанавливали вразбежку, т.е. в шахматном порядке с расстоянием
между брусками и отдельными их рядами по Бруски шероховатости сечением 8×12 см устанавливали аналогично указанному на рис. 5. В опытах данной серии через сооружение (мост) пропускали расходы: 5,8; 12,3; 19,8 и 28,3 л/сек. Поток в отводящем русле протекал по схеме свободного истечения, т. е. без подтопления со стороны нижнего бьефа.
Рис. 5. Схема модели моста и отводящего
русла с повышенной шероховатостью. Бруски сечением 6×8 мм, длиной Относительная
высота шероховатости представляет собой величину σ/н - где σ - высота бруска шероховатости; н - подпор перед сооружением (мостом).
Анализируя влияние относительной высоты шероховатости на степень гашения
скоростей в отводящем русле при различной длине участка шероховатости (рис. 6)
и σ =
Рис. 6. Влияние относительной высоты шероховатости σ/н на степень гашения скоростей в отводящем русле при различной длине участков повышенной шероховатости Сравнивая
положение кривых II и III, следует отметить, что
увеличение длины участка шероховатости lш после определенного предела приводит к
незначительному снижению скорости за укреплением.
В данном случае кривая II, соответствующая длине lш = В
частности, для кривой II скорости в среднем
больше на 6 %, чем для кривой I. Для случая, когда
высота бруска шероховатости σ =
Рис. 7. Влияние относительной высоты
выступов шероховатости на степень гашения скоростей (lш = Рассмотрим
эффективность гашения скоростей для брусков шероховатости сечением 6×8 мм, устанавливаемых через
Рис. 8. Степень гашении скоростей в отводящем русле с повышенной шероховатостью при разных расходах Можно
отметить следующее. При lш = Для
выяснения эффективности гашения скоростей измеряли скорости в сечении
отводящего русла, расположенном в
Аналогичный
эффект гашения скоростей наблюдался и для модели прямоугольной трубы отверстием
При проведении опытов было исследовано также зигзагообразное (с разрывами) расположение тех же брусков шероховатости в отводящем русле. Эффект гашения скорости при этом не повысился по сравнению с типом, упомянутым выше. В целях применения в натурных условиях полученных экспериментальных данных необходимы соответствующие пересчеты с учетом коэффициента масштаба моделей. Для малого
моста с необтекаемыми конусами и трапецеидальным поперечным сечением
подмостового русла в нашем случае на модели отверстие было Длина участка шероховатости в отводящем русле определяется соответственно выражением lш(н) = lш(м)10. Параметры потока, протекающего в отверстии моста и отводящем русле, определяются известными формулами: для
скорости Для прямоугольной трубы на модели величина отверстия была ЗАКЛЮЧЕНИЕ Повышенная шероховатость в отводящем русле из железобетонных сборных плит целесообразна, так как в этом случае: - эффект гашения скоростей увеличивается в 1,5-2 раза по сравнению с гладким руслом; -
снижение скоростей, обусловленное наличием повышенной шероховатости, позволяет
уменьшить длину укрепления отводящего русла для моста или трубы до 5- Бруски
шероховатости целесообразно располагать в шахматном порядке с расстоянием между
отдельными брусками и рядами, равным ЛИТЕРАТУРА 2. Рахманов А.Н. Размывающая способность потока в донном гидравлическом
прыжке при сильно шероховатом водобое. Известия ВНИИГ, т.
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/56240
На эту страницу сайта можно сделать ссылку:
На правах рекламы: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|