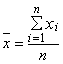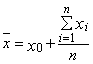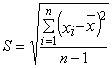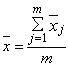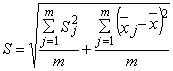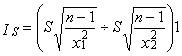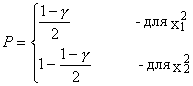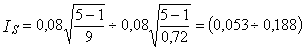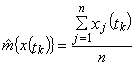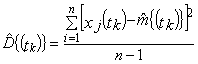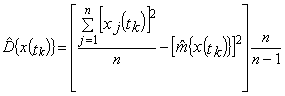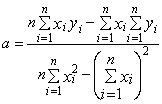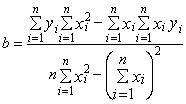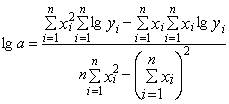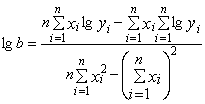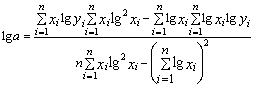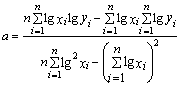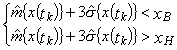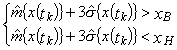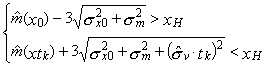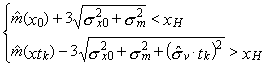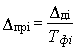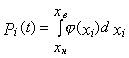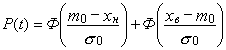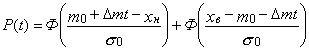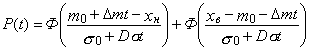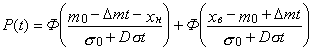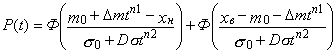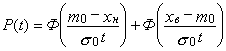
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"ГОСТ 27.202-83 Надежность в технике. Технологические системы. Методы оценки надежности по параметрам качества изготовляемой продукции.
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР НАДЕЖНОСТЬ В ТЕХНИКЕ ТЕХНОЛОГИЧЕСКИЕ СИСТЕМЫ МЕТОДЫ ОЦЕНКИ НАДЕЖНОСТИ ПО ПАРАМЕТРАМ КАЧЕСТВА ИЗГОТОВЛЯЕМОЙ ПРОДУКЦИИ ГОСТ 27.202-83 ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ Москва ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
Постановлением Государственного комитета СССР по стандартам от 28 февраля 1983г. № 980 срок введения установлен с 01.07.84 Настоящий стандарт устанавливает технические требования к методам оценки надежности технологических систем по параметрам качества изготовляемой продукции в отраслях машиностроения и приборостроения при технологической подготовке производства, а также при разработке и внедрении мероприятий по совершенствованию действующих технологических процессов и операций. Термины и определения - по ГОСТ 3.1109-82, ГОСТ 14.004-83, ГОСТ 27002-83, ГОСТ 15895-77, ГОСТ 18322-78, ГОСТ 15467-79, ГОСТ 16504-81. 1. ОБЩИЕ ПОЛОЖЕНИЯ1.1. Цели, общие требования и задачи оценки надежности технологических систем (ТС) - по ГОСТ 27.203-83. 1.2. Оценка надежности ТС по параметрам качества изготовляемой продукции содержит: выбор номенклатуры показателей надежности; определение фактических значений показателей; сравнение фактических значений с требуемыми или базовыми значениями. 1.3. Оценку надежности ТС по параметрам качества изготовляемой продукции следует производить при проведении работ, указанных в пп. 1.3.1-1.3.8. 1.3.1. Разработка технологических процессов на этапе технологической подготовки производства. 1.3.2. Управление технологическими процессами. 1.3.3. Определение периодичности подналадок технологического оборудования. 1.3.4. Выбор методов и планов статистического регулирования технологических процессов (операций). 1.3.5. Уточнение требований к качеству материалов и заготовок. 1.3.6. Выбор и корректировка планов испытаний и технического контроля готовой продукции. 1.3.7. Замена, модернизация или ремонт средств технологического оснащения. 1.3.8. Совершенствование ТС в части повышения их надежности и качества изготовляемой продукции. 1.4. В зависимости от цели и задач оценки надежности ТС по параметрам качества изготовляемой продукции используют следующие основные исходные данные: требуемые или базовые значения показателей надежности ТС; структуру и состав ТС; вид продукции, продолжительность процесса ее изготовления; объем производства; характеристики технического уровня и надежности технологического оборудования и оснастки; параметры точности заготовок; данные о нарушениях технологической дисциплины; предельные значения параметров изготовляемой продукции; точностные характеристики используемых методов и средств контроля; результаты предшествующих оценок; статистические данные, полученные в процессе внедрения и эксплуатации ТС; данные отдела технического контроля и других служб предприятия о качестве продукции. 1.5. При выборе методов оценки надежности ТС по параметрам качества изготовляемой продукции необходимо различать четыре вида (уровня рассмотрения) ТС: ТС технологической операции; ТС технологического процесса; ТС, действующие в пределах отдельного производственного подразделения (цех, участок и др.); ТС предприятия. 1.6. В зависимости от вида ТС все показатели надежности по параметрам качества изготовляемой продукции подразделяют на четыре группы: по точности (технологического процесса и средств технологического оснащения); по технологической дисциплине; по выполнению заданий по качеству (по параметрам качества продукции); комплексные показатели. Применение групп показателей надежности ТС указано в табл. 1. Таблица 1
Примечание. Знак «+» означает возможность применения группы показателей для ТС данного вида. 1.7. Продолжительность и периодичность оценки показателей надежности ТС - по ГОСТ 27.203-83. 1.8. Для оценки показателей надежности по параметрам качества изготовляемой продукции в зависимости от вида ТС и целей оценки следует использовать расчетные, опытно-статистические, регистрационные или экспертные методы. Для предварительной оценки надежности ТС по параметрам точности следует использовать также метод квалитетов. 1.9. Расчетные методы основаны: на использовании математических моделей изменения параметров качества изготовляемой продукции или параметров технологического процесса, с учетом физики отказов (качественной природы процессов износа, старения, температурных деформаций и т.п.) и имеющихся априорных данных о свойствах технологических систем данного класса; на использовании данных о закономерностях изменения во времени факторов (износ инструмента, температурные и упругие деформации и т.п.), влияющих на один или одновременно несколько параметров качества изготовляемой продукции. 1.10. Опытно-статистические (измерительные) методы основаны на использовании данных измерений параметров качества изготовляемой продукции, полученных в результате специального выборочного обследования ТС и (или) специальных испытаний ТС и ее элементов. Методы оценки показателей по опытно-статистическим данным - по ГОСТ 27.503-81, ГОСТ 11.005-74, ГОСТ 11.006-74 и ГОСТ 11.007-75. 1.11. Регистрационные методы не требуют проведения специального выборочного обследования и основаны на анализе информации, регистрируемой в процессе управления предприятием по технической документации, утвержденной в установленном порядке (результаты контроля точности технологических процессов, число принятых партий, дефектов и т.п.). Эта информация должна удовлетворять требованиям достоверности и однородности по ГОСТ 16468-79, а также быть достаточной для оценки значения искомого показателя. 1.12. Экспертные методы основаны на использовании результатов опроса экспертной группы, располагающей информацией о надежности данной технологической системы и факторах, влияющих на качество изготовляемой продукции. 1.12.1. Экспертные методы следует применять при невозможности или нецелесообразности использования расчетных, опытно-статистических или регистрационных методов (недостаточное количество информации, необходимость разработки специальных технических средств и т.п.). 1.12.2. Состав экспертной группы и методика опроса - по ГОСТ 23554.0-79. 1.13. Метод квалитетов основан на сравнении требуемых значений параметров ТС с их предельными возможными значениями, установленными в справочной и нормативно-технической документации (НТД) в зависимости от квалитетов (классов) точности применяемых. средств технологического оснащения и предметов производства. 2. ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К МЕТОДАМ ОЦЕНКИ НАДЕЖНОСТИ ТЕХНОЛОГИЧЕСКИХ СИСТЕМ ПО ПАРАМЕТРАМ ТОЧНОСТИ2.1. Целью оценки надежности ТС по параметрам точности является: определение возможности применения рассматриваемого технологического процесса для изготовления продукции с определенными параметрами качества; оценка изменений точностных характеристик ТС во времени и определение их соответствия требованиям, установленным в НТД; получение информации для регулирования технологического процесса (операции). 2.2. Оценку надежности по параметрам точности следует производить по результатам контроля точности ТС технологических процессов (операций). 2.3. Вид контроля, номенклатуру контролируемых параметров и номенклатуру показателей точности ТС следует определять в процессе анализа точности и стабильности технологических процессов (операций) и устанавливать в НТД предприятия с учетом условий, вида и объема производства. 2.3.1. В процессе анализа точности и стабильности технологических процессов (операций) определяют или уточняют: модели формирования погрешностей обработки; модели изменения точности ТС во времени; оценки параметров точности ТС; зависимости между параметрами изготовляемой продукции и параметрами ТС; зависимости между погрешностями обработки на различных операциях рассматриваемого технологического процесса; основные факторы, изменяющие точностные характеристики ТС; пути и средства повышения точности ТС в процессе эксплуатации; оптимальные стратегии технического обслуживания и ремонта средств технологического оснащения. 2.3.2. При проведении анализа точности и стабильности технологических процессов (операций) следует использовать методы прикладной статистики, теории планирования эксперимента корреляционного и регрессионного анализа. 2.4. Контроль точности ТС следует производить по альтернативному или количественному признаку. 2.5. При контроле по альтернативному признаку проверяют соответствие оснащения требованиям, установленным в НТД. 2.5.1. Контроль точности ТС по альтернативному признаку следует производить в случаях, указанных в пп. 1.3.1 и 1.3.2. 2.6. При контроле по количественному признаку определяют значения показателей точности. Основные показатели точности ТС указаны в пп. 2.6.1-2.6.4. 2.6.1. Коэффициент точности (по контролируемому параметру):
где w - поле рассеяния или разность максимального и минимального значений контролируемого параметра за установленную наработку ТС, определяемые с доверительной вероятностью g по выражению: w=l(g)·S; l(g) - коэффициент, зависящий от закона распределения контролируемого параметра и величины g. Определение поля рассеяния контролируемого параметра для доверительной вероятности g, равной 0,9973, - по справочному приложению 1; S - среднее квадратическое отклонение контролируемого параметра, определяемое по справочному приложению 2; Т - допуск на контролируемый параметр. 2.6.2. Коэффициент мгновенного рассеяния (по контролируемому параметру):
где w(t) - поле рассеяния контролируемого параметра в момент времени t. 2.6.3. Коэффициент смещения (контролируемого параметра):
где
где x0 - значение параметра, соответствующее середине поля допуска (при симметричном поле допуска значение x0 совпадает с номинальным значением параметра xном). 2.6.4. Коэффициент запаса точности (по контролируемому параметру): Kз(t)=0,5-Kс(t)-0,5Kp(t). 2.6.5. Контроль точности ТС по количественному признаку следует производить в случаях, указанных в пп. 1.3.1, 1.3.4, 1.3.7 и 1.3.8. 2.7. Для обеспечения надежности ТС по параметрам точности необходимо, чтобы в любой момент времени (в пределах установленной наработки) выполнялись требования, указанные в пп. 2.7.1, 2.7.2 и 2.7.3. 2.7.1. При контроле точности ТС по альтернативному признаку значения контролируемых параметров должны соответствовать требованиям, установленным в НТД. 2.7.2. При контроле точности ТС по количественному признаку с использованием коэффициента точности по п. 2.6.1 должно выполняться условие: Кт=Кто<1, где Кто - нормативное (предельное технически обоснованное) значение Кт. 2.7.3. При контроле точности по количественному признаку с использованием коэффициентов по пп. 2.6.2-2.6.4 должно выполняться условие: Кз(t)>0 2.8. Правила выбора средств технологического оснащения процессов контроля точности - по ГОСТ 14.306-73, средств испытаний объектов производства - по нормативно-технической документации. 2.9. При контроле точности ТС по альтернативному признаку на этапе подготовки производства следует отдавать предпочтение методу квалитетов. Примеры и условия использования метода квалитетов даны в справочном приложении 3. 2.10. При контроле точности ТС по количественному признаку на этапе подготовки производства следует использовать, главным образом, расчетные методы. Основные расчетные методы приведены в справочном приложении 4. 2.11. При контроле точности ТС на этапе изготовления продукции следует использовать, главным образом, опытно-статистические методы. Основные опытно-статистические методы определения значений параметров и показателей точности ТС приведены, соответственно, в справочных приложениях 2 и 5. 3. ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К МЕТОДАМ ОЦЕНКИ НАДЕЖНОСТИ ТЕХНОЛОГИЧЕСКИХ СИСТЕМ ПО ПАРАМЕТРАМ ТЕХНОЛОГИЧЕСКОЙ ДИСЦИПЛИНЫ3.1. Целью оценки надежности ТС по параметрам технологической дисциплины является определение уровня технологической дисциплины и характера его изменения во времени. 3.2. Оценка надежности ТС по параметрам технологической дисциплины следует производить в случаях, указанных в пп. 1.3.4 и 1.3.6, по результатам контроля технологической дисциплины. 3.3. Основные положения, планирование и порядок проведения контроля технологической дисциплины - по РД 50-540-85. 3.4. В число объектов контроля технологической дисциплины следует включать: технологические процессы, с выполнением которых связано появление брака, дефектов или возвратов продукции; технологические процессы изготовления особо ответственной продукции. 3.5. Основными показателями надежности ТС по параметрам технологической дисциплины являются средние значения соответствующих показателей технологической дисциплины за установленную наработку. Показатели технологической дисциплины по технологическому процессу, производственному подразделению и предприятию в целом - по РД 50-540-85. 3.6. Показатели технологической дисциплины следует определять регистрационным методом по РД 50-540-85. 3.7. При выборе объектов контроля, получении предварительных оценок и базовых значений допускается использовать экспертные методы. 4. ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К МЕТОДАМ ОЦЕНКИ ВЫПОЛНЕНИЯ ЗАДАНИЙ ПО ПАРАМЕТРАМ КАЧЕСТВА ИЗГОТОВЛЯЕМОЙ ПРОДУКЦИИ4.1. Оценку выполнения заданий по параметрам качества изготовляемой продукции производят с целью определения вероятности того, что ТС обеспечит изготовление продукции в соответствии с требованиями НТД. 4.2. Оценка выполнения заданий должна производиться для технологических процессов (операций), оказывающих решающее влияние на качество готовой продукции, а также по которым получены неудовлетворительные результаты оценок по разд. 2 и 3. 4.3. Оценку выполнения заданий следует производить в случаях, указанных в пп. 1.3.1; 1.3.3; 1.3.4; 1.3.6 и 1.3.8. 4.4. При оценке выполнения заданий для ТС технологических операций следует использовать, в основном, показатели, указанные в пп. 4.4.1 и 4.4.2, а для ТС производственных подразделений - показатель по п. 4.4.3. 4.4.1. Вероятность выполнения задания по одному (i-му) параметру изготовляемой продукции - вероятность выполнения требований НТД по этому параметру для единицы продукции, изготовленной в момент времени t. Pi(t)=P{xн i £ xi(t) £xв i}, где xi(t), xвi, xнi - соответственно, фактическое, верхнее и нижнее значения i-го контролируемого параметра. 4.4.2. Вероятность выполнения заданий ТС по п параметрам изготовляемой продукции - вероятность выполнения требований нормативно-технической документации одновременно по п параметрам для единицы продукции, изготовленной в момент времени t. Р1 . . . n(t) = P{xн1 £ x1(t) £ x01; . . . xн n £ xn(t) £ xв n}. 4.4.3. Коэффициент выполнения заданий по параметрам изготовляемой продукции.
где п - количество контролируемых параметров. 4.5. Наряду с показателями по пп. 4.4.1-4.4.3 допускается использовать их средние значения за установленную наработку ТС. 4.6. Значения показателей выполнения заданий для разрабатываемых ТС следует определять, главным образом, расчетными методами. Основные расчетные методы для ТС технологических операций и процессов приведены, соответственно, в справочных приложениях 6 и 7. 4.7. Значение показателей выполнения заданий для действующих ТС в общем случае следует проводить расчетными или опытно-статистическими методами. Основные опытно-статистические методы определения значений показателей выполнения заданий по параметрам качества изготовляемой продукции приведены в справочном приложении 8. 4.8. Значения показателей выполнения заданий для действующих ТС в случае выполнения условий, указанных в п. 1.1, следует определять регистрационными методами. Основные регистрационные методы определения значений показателей выполнения заданий по параметрам качества изготовляемой продукции приведены в справочном приложении 9. 5. ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К МЕТОДАМ ОЦЕНКИ КОМПЛЕКСНЫХ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ТЕХНОЛОГИЧЕСКИХ СИСТЕМ5.1. Комплексные показатели надежности ТС по параметрам качества изготовляемой продукции характеризуют надежность ТС и качество продукции, изготовленной за установленную наработку или определенный промежуток времени. 5.2. Оценку комплексных показателей надежности ТС по параметрам качества изготовляемой продукции следует производить в случаях, указанных в пп. 1.3.1; 1.3.2; 1.3.6 и 1.3.8. 5.3. Оценку надежности по комплексным показателям следует производить для всех ТС технологических процессов, производственных подразделений и предприятия в целом. 5.4. При проведении оценки следует использовать показатели, указанные в пп. 5.4.1-5.4.3. 5.4.1 Показатели надежности ТС по критериям дефектности 5.4.1.1. Коэффициент дефектности для ТС технологического процесса (производственного подразделения или предприятия) - среднее значение коэффициента (индекса) дефектности продукции, изготовленной за установленную наработку (рассматриваемый календарный промежуток времени). Коэффициент и индекс дефектности продукции - по ГОСТ 15467-79. 5.4.1.2. Вероятность соблюдения норматива по дефектности - вероятность того, что значение показателя по п. 5.4.1.1 не превысит нормативного (технико-экономически обоснованного) значения. 5.4.2. Показатели надежности ТС по критериям возвратов продукции 5.4.2.1. Коэффициент возвратов для ТС технологического процесса (производственного подразделения) - отношение объема продукции, имеющей устранимые дефекты и возвращенной на доработку с последующих, технологических процессов (из смежных производственных подразделений) по отношению к объему всей продукции, изготовленной за установленную наработку (за рассматриваемый календарный промежуток времени). Устранимый дефект - по ГОСТ 15467-79. 5.4.2.2. Процент сдачи продукции с первого предъявления для ТС технологического процесса (производственного подразделения или предприятия) - среднее значение процента сдачи с первого предъявления продукции, изготовленной за установленную наработку (за рассматриваемый календарный промежуток времени). Процент сдачи продукции с первого предъявления - по технической документации, утвержденной в установленном порядке. 5.4.2.3. Вероятность соблюдения норматива по возвратам продукции - вероятность того, что показатель по п. 5.4.2 не превысит нормативно (технико-экономически обоснованного) значения. 5.4.2.4. Вероятность соблюдения норматива по сдаче продукции с первого предъявления - вероятность, что значение соответствующего показателя по п. 5.4.2.1 будет не менее нормативного (технико-экономического обоснованного) значения. 5.4.3. Показатели надежности ТС по критериям брака 5.4.3.1. Коэффициент брака для ТС технологического процесса (производственного подразделения или предприятия) - отношение объема продукции, имеющей неустранимые критические дефекты, к объему всей продукции, изготовленной за установленную наработку (за рассматриваемый календарный промежуток времени). Критический дефект - по ГОСТ 15467-79. 5.4.3.2. Вероятность соблюдения норматива по браку - вероятность того, что значение соответствующего показателя по п. 5.4.3.1 не превысит нормативного (технико-экономически обоснованного) значения. 5.5. Возможные методы определения значений показателей по п. 4.5 указаны в табл. 2 знаком (+) Таблица 2
5.6. При выборе методов определения значений показателей по п. 5.4 следует отдавать предпочтение регистрационным методам. 5.7. Расчетные методы следует применять преимущественно на этапе технологической подготовки производств. 5.8. Экспертные методы следует применять преимущественно для предварительной оценки искомых величин. ПРИЛОЖЕНИЕ 1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
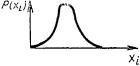
Закон распределения |
Графическое изображение |
Поле рассеяния |
Условия, при которых наблюдается данный закон |
|
Нормальный закон |
|
w=6S |
Центры рассеяния параметров во времени не смещаются |
|
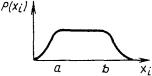
Композиция нормального закона и закона равной вероятности |
|
w= lbS |
Центры рассеяния параметров смещаются во времени по линейной зависимости |
|
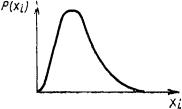
Композиция нормального закона и закона равномерно возрастающей вероятности |
|
w=(l'b+ l''b)S |
Центры рассеяния параметров смещаются по параболической зависимости |
|
Закон Максвелла |
|
w=5,25 S |
Центры рассеяния во времени не смещаются и погрешности образуются за счет несоосности, эксцентриситета и т.д. |
Значения коэффициентов lb, l'b и l''b даны в табл. 2 в зависимости от величины b, которую определяют по выражению:
![]()
где а и b - параметры плотности распределения закона равной вероятности

или закона равномерно-возрастающей вероятности
![]()
Значения коэффициентов lb, l'b, l''b
|
Коэффициенты |
В |
|||||||||||
|
3,0 |
2,4 |
2,1 |
1,8 |
1,5 |
1,2 |
1,0 |
0,8 |
0,6 |
0,4 |
0,2 |
0 |
|
|
lb |
2,00 |
2,10 |
2,15 |
2,23 |
2,30 |
2,40 |
2,50 |
2,60 |
9,70 |
2,80 |
2,90 |
3,00 |
|
L'b |
2,75 |
2,83 |
2,85 |
2,88 |
2,92 |
2,95 |
2,95 |
2,98 |
3,09 |
3,09 |
3,09 |
3,00 |
|
L''b |
- |
1,90 |
1,95 |
2,05 |
2,15 |
2,30 |
2,40 |
2,50 |
2,65 |
2,75 |
2,90 |
3,00 |
ПРИЛОЖЕНИЕ 2
Справочное
ОПЫТНО-СТАТИСТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ТОЧНОСТИ ТС ТЕХНОЛОГИЧЕСКИХ ОПЕРАЦИЙ
1. Определение параметров точности ТС опытно-статистическими методами производится на основе статистической обработки мгновенных выборок.
2. Расчет среднего значения и среднего квадратического отклонения по одной выборке.
2.1. Среднее значение или центр рассеяния определяют по формуле
если результаты измерения xi записаны в абсолютных значениях параметра, и по формуле
если результаты измерения хi записаны в отклонениях от заданного начала отсчета х0.
2.2. Пример. При обработке вала по диаметру 13,3h8-0,27 на токарном автомате в мгновенной выборке, состоящей из пяти деталей, были получены отклонения диаметра от начала отсчета, которое было принято равным 13 мм; 0,25; 0,28; 0,26; 0,1; 0,14 мм.
По формуле (2) определяем
![]()
2.3. Среднее квадратическое отклонение определяют по формуле
или по формуле
где R=xmах-xmin - величина размаха в мгновенной выборке;
xmах-xmin - максимальное и минимальное значения в мгновенной выборке;
dn - коэффициент, изменяющийся в зависимости и от объема n мгновенной выборки и определяемый по табл. 1.
|
n |
dn |
n |
dn |
|
2 |
1,12 |
12 |
3,258 |
|
3 |
1,693 |
13 |
3,336 |
|
4 |
2,059 |
14 |
3,407 |
|
5 |
2,326 |
15 |
3,472 |
|
6 |
2,534 |
16 |
3,532 |
|
7 |
2,704 |
17 |
3,588 |
|
8 |
2,847 |
18 |
3,640 |
|
9 |
2,970 |
19 |
3,689 |
|
10 |
3,078 |
20 |
3,735 |
|
11 |
3,173 |
|
|
2.4. Пример. Определить среднее квадратическое отклонение по данным п. 2.2. По формуле (3) определяем
![]() .
.
По формуле (4) определяем ту же величину
![]() ,
,
Где величину 2,326=dn определяем по табл. 1 для n=5.
3. Расчет среднего значения и среднего квадратического отклонения по нескольким мгновенным выборкам
3.1. Среднее значение рассчитывают по формуле
где хj - среднее значение j-й мгновенной выборки;
m - число мгновенных выборок.
3.2. Пример. Определить среднее значение контролируемого параметра по данным четырех мгновенных выборок, полученных при обработке вала диаметром 13,3h8-0,27 и приведенных в табл. 2.
По формуле (1) рассчитывают среднее значение хj контролируемого параметра для каждой мгновенной выборки. Результаты расчета приведены в нижней строке табл. 2.
|
Номер детали в выборке |
Номер выборки |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
13,25 |
13,18 |
13,19 |
13,13 |
|
2 |
13,28 |
13,22 |
13,20 |
13,13 |
|
3 |
13,26 |
13,14 |
13,22 |
13,29 |
|
4 |
13,10 |
13,20 |
13,28 |
13,21 |
|
5 |
13,14 |
13,25 |
13,25 |
13,20 |
|
хj |
13,206 |
13,178 |
13,228 |
13,192 |
По формуле (5) определяем искомое среднее значение
![]() .
.
3.3. Среднее квадратическое отклонение по нескольким мгновенным выборкам одинакового объема рассчитывают по формуле
где Sj - среднее квадратическое отклонение в j-й мгновенной выборке, определяемое по п. 2.3.
3.4. Пример. Определить среднее квадратическое отклонение по данным п. 3.2 (табл. 2).
Определяем величину sj для каждой мгновенной выборки по формуле (3) п. 2.3.
Результаты расчетов сведены в табл. 3.
Таблица 3
|
Номер выборки |
1 |
2 |
3 |
4 |
|
sj |
0,080 |
0,033 |
0,037 |
0,066 |
По формуле (6) определяем искомую величину
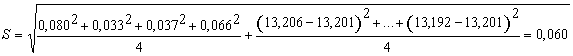
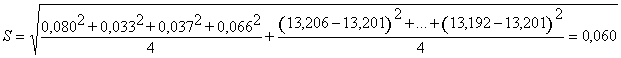
3.5. В некоторых случаях среднее квадратическое отклонение с достаточной для практики точностью можно определить методом размахов. В этом случае используют формулу
![]() ,
,
где Rj - величина размаха в j-й мгновенной выборке.
3.6. Пример. Определить среднее квадратическое отклонение методом размахов по данным п. 3.2 (табл. 2). Определяем величины Rj как разность максимального и минимального значений параметра в j-й мгновенной выборке. Результаты расчетов сведены в табл. 4.
Таблица 4
|
Номер выборки |
1 |
2 |
3 |
4 |
|
Rj |
0,18 |
0,08 |
0,09 |
0,13 |
Определяем искомую величину по формуле (7):
![]()
4. Оценку достоверности полученных значений параметров точности по пп. 2 и 3 следует производить методом доверительных интервалов, исходя из общего объема выборки n.
4.1. Доверительным интервалом для величины х будет интервал
![]() , (8)
, (8)
в котором e определяют по формуле
где tg - квантиль распределения Стьюдента, определяемый для заданной доверительной вероятности g, по табл. 5 в зависимости от уровня значимости а=1-g и числа степеней свободы k=n-1;
S - среднее квадратическое отклонение в выборке.
Значения квантилей распределения Стьюдента tg
|
К |
Уровень значимости а |
||||||
|
0,80 |
0,40 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
|
|
1 |
0,325 |
1,376 |
3,078 |
6,314 |
12,706 |
31,821 |
63,657 |
|
2 |
0,289 |
1,061 |
1,886 |
2,920 |
4,303 |
6,965 |
9,925 |
|
3 |
0,277 |
0,978 |
1,638 |
2,353 |
3,182 |
4,541 |
5,841 |
|
4 |
0,271 |
0,941 |
1,533 |
2,132 |
2,776 |
3,747 |
4,604 |
|
5 |
0,267 |
0,920 |
1,476 |
2,015 |
2,571 |
3,365 |
4,032 |
|
6 |
0,265 |
0,906 |
1,440 |
1,943 |
2,447 |
3,143 |
3,707 |
|
7 |
0,263 |
0,896 |
1,415 |
1,895 |
2,365 |
2,998 |
3,499 |
|
8 |
0,262 |
0,889 |
1,397 |
1,860 |
2,306 |
2,896 |
3,355 |
|
9 |
0,261 |
0,883 |
1,383 |
1,833 |
2262 |
2,821 |
3,250 |
|
10 |
0,260 |
0,879 |
1,372 |
1,812 |
2,228 |
2,764 |
3,169 |
|
11 |
0,260 |
0,876 |
1,363 |
1,796 |
2,201 |
2,718 |
3,106 |
|
12 |
0,259 |
0,873 |
1,356 |
1,782 |
2,179 |
2,681 |
3,055 |
|
13 |
0,259 |
0,870 |
1,350 |
1,771 |
2,160 |
2,650 |
3,012 |
|
14 |
0,258 |
0,868 |
1,345 |
1,761 |
2,145 |
2,624 |
2,977 |
|
15 |
0,258 |
0,866 |
1,341 |
1,753 |
2,131 |
2,602 |
2,947 |
|
16 |
0,258 |
0,865 |
1,337 |
1,746 |
2,120 |
2,583 |
2,921 |
|
17 |
0,257 |
0,863 |
1,333 |
1,740 |
2,110 |
2,567 |
2,898 |
|
18 |
0,257 |
0,862 |
1,330 |
1,734 |
2,101 |
2,552 |
2,878 |
|
19 |
0,257 |
0,861 |
1,328 |
1,729 |
2,093 |
2,539 |
2,861 |
|
20 |
0,257 |
0,860 |
1,325 |
1,725 |
2,086 |
2,528 |
2,845 |
|
21 |
0,257 |
0,859 |
1,323 |
1,721 |
2,080 |
2,518 |
2,831 |
|
22 |
0,256 |
0,858 |
1,321 |
1,717 |
2,074 |
2,508 |
2,819 |
|
23 |
0,256 |
0,858 |
1,319 |
1,714 |
2,069 |
2,500 |
2,807 |
|
24 |
0,256 |
0,857 |
1,318 |
1,711 |
2,064 |
2,492 |
2,797 |
|
25 |
0,256 |
0,856 |
1,316 |
1,708 |
2,060 |
2,485 |
2,787 |
|
26 |
0,256 |
0,856 |
1,315 |
1,706 |
2,056 |
2,479 |
2,779 |
|
27 |
0,256 |
0,855 |
1,314 |
1,703 |
2,052 |
2,473 |
2,771 |
|
28 |
0,256 |
0,855 |
1,313 |
1,701 |
2,048 |
2,467 |
2,763 |
|
29 |
0,256 |
0,854 |
1,311 |
1,699 |
2,045 |
2,462 |
2,756 |
|
30 |
0,256 |
0,854 |
1,310 |
1,697 |
2,042 |
2,457 |
2,750 |
|
40 |
0,255 |
0,851 |
1,303 |
1,684 |
2,021 |
2,423 |
2,704 |
|
60 |
0,254 |
0,848 |
1,296 |
1,671 |
2,000 |
2,390 |
2,660 |
|
120 |
0,254 |
0,845 |
1,289 |
1,658 |
1,980 |
2,358 |
2,617 |
|
¥ |
0,253 |
0,842 |
1,282 |
1,645 |
1,960 |
2,326 |
2,576 |
4.2. В случае, если параметр х распределен по нормальному закону, его доверительный интервал определяют по формуле
где величины ![]() и
и ![]() (значения критерия
согласия Пирсона) определяют по табл. 6 в зависимости от числа k=n-1 и
вероятности Р
(значения критерия
согласия Пирсона) определяют по табл. 6 в зависимости от числа k=n-1 и
вероятности Р
Таблица 6
Значения х2 в зависимости от Р и k=n-1
|
k |
Р |
|||||
|
0,005 |
0,025 |
0,05 |
0,95 |
0,995 |
0,999 |
|
|
1 |
7,80 |
5,00 |
3,80 |
0,004 |
0,001 |
0,00 |
|
3 |
13,00 |
9,30 |
7,80 |
0,35 |
0,20 |
0,01 |
|
5 |
17,00 |
12,70 |
11,00 |
1,10 |
0,83 |
0,15 |
|
7 |
20,50 |
16,00 |
14,00 |
2,20 |
1,70 |
0,60 |
|
10 |
25,00 |
20,50 |
18,50 |
4,00 |
3,20 |
1,50 |
|
15 |
33,00 |
27,50 |
25,00 |
7,40 |
6,20 |
3,40 |
|
20 |
40,00 |
34,00 |
31,00 |
11,00 |
9,60 |
6,00 |
|
25 |
47,00 |
40,50 |
38,00 |
14,50 |
13,00 |
8,60 |
|
30 |
54,00 |
47,00 |
44,00 |
18,50 |
16,70 |
11,50 |
|
36 |
62,00 |
54,00 |
51,00 |
23,00 |
20,21 |
15,00 |
|
40 |
66,00 |
60,00 |
66,00 |
26,00 |
24,00 |
18,00 |
|
46 |
74,00 |
66,00 |
62,00 |
31,00 |
29,00 |
21,00 |
|
50 |
78,00 |
72,00 |
68,00 |
35,00 |
32,00 |
24,00 |
|
56 |
86,00 |
78,00 |
74,00 |
40,00 |
37,00 |
28,00 |
|
60 |
92,00 |
84,00 |
78,00 |
41,00 |
40,00 |
31,00 |
|
66 |
98,00 |
90,00 |
86,00 |
48,00 |
46,00 |
36,00 |
|
70 |
104,00 |
95,00 |
90,00 |
52,00 |
48,00 |
39,00 |
Доверительная вероятность g обычно принимается достаточно большой и равной 0,9; 0,95; 0,99 в зависимости от уровня требований, предъявляемых к качеству изготовляемой продукции.
4.3. Пример. Определить доверительный интервал для величин
![]() =13,206 и
=13,206 и
S=0,08,
рассчитанных в пп. 2.2 и 2.4 при общем объеме выборки n=5.
4.4.1. Определяем доверительный интервал для ![]() по выражению (8)
по выражению (8)
![]() .
.
Задаваясь доверительной вероятностью g=0,9, определяем уровень значимости
а=1-g=0,1.
По табл. 5 для а=0,1 и k=n-1=4 находим значение квантиля распределения Стьюдента tg=2,132.
Рассчитываем величину e по формуле (9):
![]() .
.
Следовательно, Iх=(13,121¸13,291).
4.4.2. Определяем доверительный интервал для S по выражению (10)
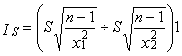 ,
,
Задаваясь доверительной вероятностью g=0,9, определяем вероятности Р по выражению (11)
![]() ;
; ![]() .
.
По табл. 6 для k=n-1=4 находим значения критериев согласия Пирсона
![]() =9,
=9, ![]() =0,72.
=0,72.
Следовательно,
ПРИЛОЖЕНИЕ 3
Справочное
ОЦЕНКА ТОЧНОСТИ ТЕХНОЛОГИЧЕСКОЙ СИСТЕМЫ МЕТОДОМ КВАЛИТЕТОВ
1. Оценка точности технологической системы методом квалитетов производится на этапе технологической подготовки производства при наличии справочной или нормативно-технической документации (базовой документации), регламентирующей возможные значения параметров качества изготовляемой продукции в зависимости от квалитетов (классов точности) применяемых средств технологического оснащения и предметов производства.
2. Оценка точности технологических систем технологической операции считается удовлетворительной при выполнении следующих условий:
требуемые значения параметров точности изготовляемой продукции должны принадлежать области их возможных значений, установленных (регламентированных) в базовой документации (например, соответствовать допустимым отклонениям аналогичных параметров образца-изделия при проверке точности средств технологического оснащения в работе);
условия функционирования ТС (температура, влажность, уровень вибраций и т.п.), техническое состояние применяемых средств технологического оснащения (биение шпинделя, жесткость и т.п.) и параметры используемых предметов производства (твердость материала, шероховатость поверхности и т.п.) должны соответствовать требованиям, установленным в базовой документации (в части условий получения регламентированных значений параметров точности изготовляемой продукции).
3. Допускается применять метод квалитетов при отдельных нарушениях требований по п. 2, если эти нарушения не влияют на точность обработки, а также если известная максимальная величина отклонения рассматриваемого параметра в следствии указанных нарушений и скорректированная на эту величину область возможных значений параметра удовлетворяет требованиям НТД.
4. Пример. Оценить точность ТС токарной операции методом квалитетов.
4.1. Исходные данные. Операцию производят на автомате продольного точения мод. 1П16 класса точности П; в качестве заготовки используют пруток диаметром 16 мм из автоматной прутковой стали; максимальное возможное смещение режущей кромки резца (из-за его износа, тепловых деформаций и т.п.) по справочным данным не превосходит 7 мкм; допуск на обработку контролируемого параметра диаметром 14h8 равен 27 мкм.
4.2. По ГОСТ 8831-79 находим, что допуск на диаметр образца-изделия в поперечном сечении равен 8 мкм.
4.3. Определяем область возможных отклонений контролируемого параметра по п. 3 (равную сумме допуска на диаметр образца-изделия и удвоенной абсолютной величины смещения режущей кромки резца):
dS=8+2·7=22 мкм.
4.4. Сравнивая величину dS с допуском на обработку контролируемого параметра диаметром 14h8, в соответствии с п. 2 делаем вывод о том, что точность рассматриваемой ТС следует считать удовлетворительной.
ПРИЛОЖЕНИЕ 4
Справочное
РАСЧЕТНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ ТОЧНОСТИ ТЕХНОЛОГИЧЕСКИХ СИСТЕМ
1. Метод случайных функций
1.1. Определение показателей точности ТС технологических операций методом случайных функций производится расчетом характеристик случайного процесса изменения контролируемого параметра x(t): математического ожидания m{x(t)} и дисперсии D{x(t)}.
1.2. Исходные данные для определения величин m{x{t)} и D{x(t)} получают в ходе выборочного обследования не менее десяти реализации технологического процесса.
1.2.1. Полученные в результате обследования значения контролируемых параметров деталей заносят в таблицу (см. табл. 1), в которой через t1, t2, ..., tk, ..., t1 ..., tm обозначают номера последовательно обрабатываемых деталей одной партии (или моменты времени проведения измерений), а через x1(t), x2(t), xn(t) обозначают отдельные реализации технологического процесса (партии или выборки из партии).
|
x(t) |
t |
|||||||
|
t1 |
t2 |
… |
tk |
… |
t1 |
... |
(tm) |
|
|
x1(t) |
x1(t1) |
x1(t2) |
… |
x1(tk) |
… |
x1(t1) |
… |
x1(tm) |
|
x2(t) |
x2(t1) |
x2(t2) |
… |
x2(tk) |
… |
x2(t1) |
… |
x2(tm) |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
xj(t) |
xj(t1) |
xj(t2) |
… |
xj(tk) |
… |
xj(t1) |
… |
xj(tm) |
|
… |
|
|
… |
|
… |
|
… |
|
|
xn(t) |
xn(t1) |
xn(t2) |
… |
xn(tk) |
… |
xn(t1) |
… |
xn(tm) |
1.2.2. Значения t1, t2, .., tm следует задавать равноотстоящими (t2-t1=t3-t2=tm-tm-1).
1.2.3. В зависимости от объема партий разность следует брать таким образом, чтобы количество измеряемых деталей m в одной партии или реализации было не менее, десяти.
1.2.4. Оценки математических ожиданий ![]() {x(tk)} и дисперсий
{x(tk)} и дисперсий ![]() {x(tk)} вычисляют по формулам:
{x(tk)} вычисляют по формулам:
или
где xj(tk) - значение j-й реализации в момент tk;
n - количество реализации.
1.2.5. Вычисленные по формулам
(1), (2), (3) значения ![]() {x{tk)},
{x{tk)}, ![]() {x{tk)} следует выравнивать по формулам, приведенным в табл. 2.
{x{tk)} следует выравнивать по формулам, приведенным в табл. 2.
1.2.6. Если мгновенное поле рассеяния контролируемого параметра постоянно в процессе обработки партии деталей, а уровень настройки постоянный или смещается по линейной зависимости, каждую реализацию следует представлять линейной функцией вида
![]() (tk)=uj·tk+x0j, (4)
(tk)=uj·tk+x0j, (4)
где tk=t1; t2; …, tm - момент окончания обработки k-й детали;
![]() (tk) - значение уровня настройки в tk-й момент
времени;
(tk) - значение уровня настройки в tk-й момент
времени;
x0j - случайная величина погрешности настройки j-й реализации;
uj - случайная величина скорости смещения уровня настройки, численно равная тангенсу угла наклона прямой.
1.2.7. Для. любого tk по всем реализациям находят оценки: среднего квадратического отклонения случайной погрешности
![]() , (5)
, (5)
где Sm - оценка среднего квадратического отклонения
математического ожидания погрешности настройки ![]() (х0), характеризующего фактический уровень
настройки
(х0), характеризующего фактический уровень
настройки
![]() ; (6)
; (6)
|
Функция |
Формулы для определения постоянных по способу наименьших квадратов |
График функций |
|
|
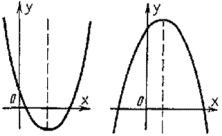
y=ax+b |
|
|
|
|
y=ax2+bx+c |
|
|
|
|
y=abx или lgy=lga+xlgb |
|
|
|
|
y=axb или lgy=lga+blgx |
|
|
|
дисперсии погрешности настройки
![]() ; (7)
; (7)
математического ожидания ![]() (u) скорости
смещения уровня настройки
(u) скорости
смещения уровня настройки
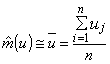 ; (8)
; (8)
дисперсии скорости смещения уровня настройки
![]() . (9)
. (9)
1.3. Коэффициент точности ТС технологической операции вычисляют по формуле, приведенной в п. 2.6.1 настоящего стандарта. При этом w определяют по следующим формулам:
при смещении уровня настройки к верхнему предельному отклонению контролируемого параметра
![]() ; (10)
; (10)
при смещении уровня настройки к нижнему предельному отклонению контролируемого параметра
![]() . (11)
. (11)
1.4. Коэффициент точности ТС технологической операции для случаев, когда каждую реализацию представляют линейной функцией, вычисляют по формуле, приведенной в п. 2.6.1 настоящего стандарта. При этом w (для любых случаев смещения уровня настройки) определяют по формуле
![]()
![]() . (12)
. (12)
1.5. Для обеспечения надежности ТС технологической
операции по точности при определении функции ![]() {x(t)} и
{x(t)} и ![]() {x(t)} по п. 1.2.4, необходимо, чтобы в моменты tk выполнялись следующие неравенства:
{x(t)} по п. 1.2.4, необходимо, чтобы в моменты tk выполнялись следующие неравенства:
при смещении уровня настройки к верхней границе поля допуска
где хв, хн - соответственно, верхнее и нижнее предельные значения контролируемого параметра;
![]() - среднее квадратическое отклонение
контролируемого параметра, вычисленное для момента времени tk по всем реализациям;
- среднее квадратическое отклонение
контролируемого параметра, вычисленное для момента времени tk по всем реализациям;
при смещении уровня настройки к нижней границе поля допуска
1.6. Для обеспечения надежности ТС технологической операции
по точности при определении функций ![]() {x(t)} и
{x(t)} и ![]() {x(t)} по пп. 1.2.6 и 1.2.7
необходимо, чтобы в моменты tк, выполнялись следующие неравенства:
{x(t)} по пп. 1.2.6 и 1.2.7
необходимо, чтобы в моменты tк, выполнялись следующие неравенства:
при смещении уровня настройки к верхней границе поля допуска
при смещении уровня настройки к нижней границе поля допуска
1.7. В случае единичного и мелкосерийного производства для обеспечения надежности ТС технологической операции по точности в выражения (13), (14), (15), (16) в качестве исходных данных {xj(tk), j=1...n; k=1...m} следует подставлять значения приведенных отклонений, определяемые по справочному приложению 5.
1.8. Пример. Определить коэффициент точности ТС токарной операции по данным выборочного обследования десяти реализации, указанным в табл. 3, и для допуска Т=30 мкм.
1.8.1. Определяем значения ![]() {х(tk)}
и
{х(tk)}
и ![]() {х(tk)}
по формулам
(1) и (3) и среднее квадратическое отклонение из
выражения
{х(tk)}
по формулам
(1) и (3) и среднее квадратическое отклонение из
выражения ![]() для каждого момента
времени tk (R=1... 10).
для каждого момента
времени tk (R=1... 10).
Результаты вычислений ![]() {х(tk)}
и
{х(tk)}
и ![]() {х(tk)}
даны в табл. 3.
{х(tk)}
даны в табл. 3.
|
x(t) |
t |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
x1(t) |
18 |
18 |
16 |
14 |
10 |
7 |
4 |
2 |
2 |
2 |
|
x2(t) |
18 |
14 |
16 |
10 |
10 |
6 |
7 |
2 |
3 |
2 |
|
x3(t) |
15 |
10 |
10 |
6 |
7 |
3 |
4 |
2 |
3 |
1 |
|
x4(t) |
20 |
15 |
13 |
8 |
9 |
5 |
5 |
2 |
3 |
2 |
|
x5(t) |
16 |
10 |
9 |
6 |
7 |
1 |
3 |
1 |
3 |
2 |
|
x6(t) |
16 |
14 |
9 |
8 |
4 |
4 |
2 |
3 |
2 |
5 |
|
x7(t) |
14 |
13 |
9 |
8 |
4 |
4 |
1 |
2 |
1 |
8 |
|
x8(t) |
11 |
11 |
6 |
6 |
2 |
3 |
1 |
1 |
5 |
6 |
|
x9(t) |
17 |
13 |
10 |
11 |
6 |
7 |
4 |
6 |
5 |
9 |
|
x10(t) |
18 |
18 |
13 |
13 |
9 |
9 |
7 |
9 |
8 |
11 |
|
|
16,3 |
16,6 |
11,1 |
9,0 |
6,8 |
4,9 |
3,8 |
3,0 |
3,5 |
4,8 |
|
|
2,53 |
2,87 |
3,28 |
2,88 |
2,77 |
2,72 |
2,14 |
2,54 |
2,02 |
3,54 |
1.8.2. Рассчитываем коэффициент точности по п. 1.6.
![]()
2. Метод элементарных погрешностей
2.1. Оценка показателей точности ТС технологической операции методом элементарных погрешностей производится на основе расчета суммарной погрешности контролируемого параметра. При этом исходными данными являются значения величин элементарных погрешностей (погрешность установки детали в приспособлении, геометрическая погрешность технологического оборудования, погрешность настройки оборудования, погрешности, вызываемые тепловыми деформациями и т.д.).
2.2. Данный метод следует применять на этапе технологической подготовки производства, когда нецелесообразно производить выборочно обследование технологического процесса.
2.3. Если элементарные погрешности взаимно независимы, суммарную погрешность dS контролируемого параметра определяют по формуле
где D1, D2,..., Dn - предельные значения элементарных погрешностей;
К - коэффициент риска;
l1, l2,…, ln - коэффициенты, учитывающие закон распределения элементарных погрешностей.
2.3.1. Коэффициент риска К, выбирают в зависимости от принятого риска Р.
При нормальном законе распределения элементарных погрешностей и равновероятном их выходе за обе границы поля допуска значение Р связано со значением функции Лапласа Ф(К) формулой
Р=100[1-2Ф(K)]%. (18)
Ряд значений коэффициента К приведен в табл. 4.
|
Р, % |
32,00 |
10,00 |
4,50 |
1,00 |
0,27 |
0,10 |
0,01 |
|
K |
1,00 |
1,65 |
2,00 |
2,57 |
3,00 |
3,29 |
3,89 |
2.3.2. Коэффициенты l1, l2,…, ln рассчитывают по ГОСТ 19415-74 при наличии фактических данных о законе распределения элементарных погрешностей.
При нормальном законе распределения коэффициента l1, l2,…, ln равны 0,111.
2.4. Для обеспечения надежности ТС технологической операции по точности необходимо, чтобы соблюдалось неравенство:
dS<Т.
2.5. Коэффициент точности ТС технологической операции вычисляют по формуле, приведенном в п. 2.6.1 настоящего стандарта, причем за величину w принимают суммарную погрешность dS.
2.6. Пример. Определить коэффициент точности ТС операции обработки корпусной заготовки, закрепленной в приспособлении на столе вертикально-фрезерного станка, торцевой фрезой, установленной в шпинделе (при помощи оправки).
2.6.1. Исходные данные. В соответствии со схемой фрезерования суммарная погрешность контролируемого параметра включает следующие элементарные погрешности:
геометрическую погрешность станка D1=30 мкм;
погрешность базирования D2=0 (вследствие совпадения измерительной и установочной базы);
погрешность закрепления D3=20 мкм;
погрешность изготовления приспособления D4==20 мкм;
погрешность изготовления инструмента D5=0 (предполагаем, что настройку на размер ведут по наиболее выступающему зубу фрезы, а, следовательно, биение зубьев не влияет на контролируемый параметр);
погрешность настройки фрезы на размер D6=40 мкм;
погрешность, связанная с размерным износом инструмента D7=0 (считаем, что ее можно компенсировать поднастройкой фрезы);
погрешность измерений D8=90 мкм;
погрешность, вызванная отжатием фрезы от заготовки под действием сил резания D9=30 мкм.
Допуск на контролируемый параметр Т равен 200 мкм.
2.62. Определяем величину суммарной погрешности контролируемого параметра dS.
При этом значения коэффициентов l1,…, l9 принимаем равными 0,111, полагая, что условия обработки заготовки таковы, что распределение элементарных погрешностей будет близким к закону Гаусса.
Принимаем риск Р=1% и по табл. 4 находим значение К=2,57.
Определяем искомую величину dS по формуле (17)
![]() мкм.
мкм.
2.6.3. Определяем коэффициент точности по п. 2.5:
![]()
ПРИЛОЖЕНИЕ 5
Справочное
ОПЫТНО-СТАТИСТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ ТОЧНОСТИ ТЕХНОЛОГИЧЕСКИХ СИСТЕМ
1. Метод точечных диаграмм
1.1. Контроль точности по альтернативному признаку для ТС технологической операции по методу точечных диаграмм производят построением графиков (точечных диаграмм), на которых по оси абсцисс откладывают условные номера обрабатываемых заготовок в последовательности их обработки (или время окончания их обработки), по оси ординат - измеренные значения контролируемого параметра и сравнением их с заданными предельными значениями XВ и ХН.
Графики строятся по данным протоколов измерений.
1.2. В зависимости от цели исследования и вида технологического процесса на один график наносят заданные предельные значения контролируемого параметра и результаты измерения деталей выборок.
1.2.1. Выборки производятся из одной партии деталей, последовательно обработанных на одной единице технологического оборудования при одной настройке. Схематическое изображение одной точечной диаграммы случайного процесса изменения значений контролируемого параметра x(t) приведено на черт. 1.
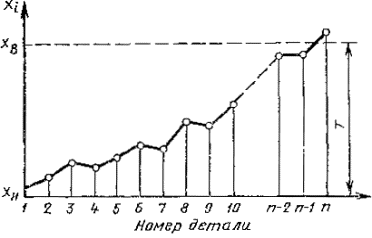
Т - допуск на контролируемый параметр
Черт. 1
По данному графику проводится контроль точности одной конкретной реализации технологического процесса.
1.2.2. Выборки производят из нескольких партий деталей, полученных в результате обработки деталей на одной единице технологического оборудования при различных ее настройках или заменах инструмента.
В этом случае на график наносят несколько реализации случайного процесса изменения значений контролируемого параметра x(t), полученных на одной единице технологического оборудования, схематическое изображение которых приведено на черт. 2.
По данному графику проводится контроль точности ТС технологической операции.
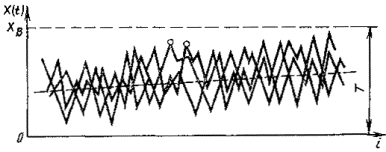
Черт. 2
1.2.3. Выборки производятся из нескольких партий деталей, полученных в результате различной обработки одноименных деталей при различных настройках на нескольких единицах технологического оборудования, выполняющих одинаковую операцию.
В данном случае на график наносят несколько реализации случайного процесса изменения значений контролируемого параметра x(t), полученных на нескольких единицах технологического оборудования.
По данному графику можно проводить контроль точности применительно ко всей совокупности единиц технологического оборудования, выполняющих данную операцию.
1.3. При построении графиков по п. 1.2 за одну реализацию следует принимать значения контролируемого параметра, полученные при постоянных условиях обработки (одна партия, одна настройка, один инструмент и т.п.).
2. Метод мгновенных выборок
2.1. Определение показателей точности ТС производят путем отбора мгновенных выборок из потока продукции. Мгновенная выборка - по ГОСТ 15395-70.
2.2. Определение показателей точности ТС технологической операции, в общем случае, проводится по данным объединенной выборки, состоящей из серий мгновенных выборок, взятых через определенные интервалы времени изготовления партии установленного объема при различных уровнях факторов, влияющих на точностные характеристики ТС.
При этом, в зависимости от целей проверки, за партию установленного объема принимают:
партию деталей, обработанных при одной настройке на одной единице технологического оборудования;
партию деталей, обработанных при нескольких настройках на одной единице технологического оборудования;
партию деталей, обработанных при нескольких настройках на нескольких единицах технологического оборудования, выполняющих одинаковую операцию.
2.3. Коэффициент точности ТС определяют по п. 2.6.1 настоящего стандарта.
При этом величину и вычисляют по формуле
w=xmax-xmin,
где - xmax, xmin - максимальное и минимальное значения контролируемого параметра в объединенной выборке.
3. Метод приведенных отклонений
3.1. Контроль точности ТС по альтернативному признаку методом приведенных отклонении производится расчетом приведенных отклонений (под которыми понимается отклонение контролируемого параметра относительно его номинального значения, выраженное в относительных единицах) и проверкой соответствия их требуемым значениям.
3.2. Данный метод применяют в условиях единичного и мелкосерийного производства, когда количество обрабатываемых одноименных деталей меньше объема, необходимого для определения показателя точности ТС расчетными методами.
3.3. Расчет приведенных отклонений производится по выборкам. В одну выборку должны включаться детали, характеризующиеся конструктивным подобием, общностью технологического процесса обработки (методы обработки применяемое технологическое оборудование и оснастка, материал заготовки и т.д.) и отличающиеся номинальными значениями контролируемого параметра (размера).
3.4. Измеренные отклонения размеров деталей, объединенных в одну выборку, приводят к единому масштабу вычислением приведенных отклонений.
3.5. Приведенные отклонения (Dпpi) вычисляют по формулам:
при расчете относительно нижнего предельного отклонения Dнi (см черт. 3), соответствующего данному номинальному размеру
где Dпрi - приведенное отклонение размера i-й детали;
Dдi - действительное отклонение размера i-й детали;
Dнi - нижнее предельное отклонение размера i-й детали;
Ti - допуск на размер i-й детали;
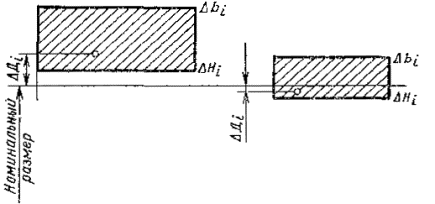
при расчете относительно верхнего предельного отклонения Dвi, соответствующего данному номинальному размеру
при расчете относительно координаты середины поля допуска Dоi, соответствующей данному номинальному размеру
Расчет приведенных отклонений одной выборки следует проводить только по одной из приведенных выше формул.
3.6. Приведенные отклонения для параметров формы и расположения поверхностей деталей, объединенных в одну выборку, вычисляют по формуле
где Тфi – допуск на параметр формы или расположения поверхностей i-й детали.
3.7. Точность ТС технологической операции считается удовлетворительной при выполнении одного из следующих условий:
3.7.1. Если приведенное отклонение рассчитано по формулам (1), (2), (4):
0 £ Dпрi £ 1. (5)
3.7.2. Если приведенное отклонение рассчитано по формуле (3):
-1 £ Dпрi £ 1. (6)
3.8. Пример. Произвести контроль точности ТС технологической операции методом приведенных отклонений.
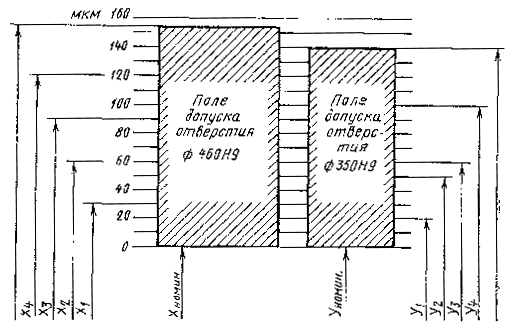
3.8.1. Исходные данные. В результате измерения размеров отверстий диаметром 450Н9 и диаметром 350Н9 получены следующие восемь значений:
x1 = 460,03 мм;
х2 = 460,06 мм;
х3 = 460,09 мм;
х4 = 460,12 мм;
y1 = 350,02 мм;
y2 = 350,05 мм;
y3 = 350,06 мм;
y4 = 350,10 мм.
На черт. 4 показано расположение отклонений измеренных размеров в пределах своих полей допусков.
3.8.2. Определяем приведенные отклонения по формуле (1):
для отверстия диаметром 460Н9:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
для отверстия диаметром 350Н9:
![]() ;
;
![]() ;
;
![]() ;
;
![]()
3.8.3. Поскольку рассчитанные приведенные отклонения удовлетворяют условию (5), то, в соответствии с п. 3.7, точность ТС следует считать удовлетворительной.
ПРИЛОЖЕНИЕ 6
Справочное
РАСЧЕТНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ ВЫПОЛНЕНИЯ ЗАДАНИЙ ПО ПАРАМЕТРАМ КАЧЕСТВА ИЗГОТОВЛЯЕМОЙ ПРОДУКЦИИ ДЛЯ ТЕХНОЛОГИЧЕСКИХ ОПЕРАЦИЙ
1. Показатели выполнения заданий по параметрам качества изготовляемой продукции определяют по известным законам и функциям распределения этих параметров.
2. В общем случае вероятность выполнения задания ТС технологической операции по i-му параметру качества изготовляемой продукции в фиксированный момент времени t определяют по формуле
где j(xi) - плотность распределения i-го параметра в момент времени t;
xв, xн - соответственно верхнее и нижнее предельные значения контролируемого параметра.
2.1. Если контролируемый параметр распределен по нормальному закону с плотностью
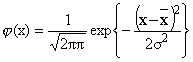 , (2)
, (2)
где ![]() , s - соответственно, среднее значение и среднее квадратическое отклонение
контролируемого параметра, определяемые по справочному приложению 2, то искомый показатель вычисляют по
формуле.
, s - соответственно, среднее значение и среднее квадратическое отклонение
контролируемого параметра, определяемые по справочному приложению 2, то искомый показатель вычисляют по
формуле.
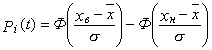 , (3)
, (3)
где
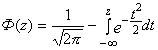 .
.
Значения функции Ф(z) приведены в табл. 1.
Таблица 1
Значения функции нормального распределения j(z)
|
z |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0,0 |
,5000 |
,5040 |
,5080 |
,5120 |
,5160 |
,5199 |
,5239 |
,5279 |
,5319 |
,5359 |
|
0,1 |
,5398 |
,5438 |
,5478 |
,5517 |
,5557 |
,5596 |
,5636 |
,5675 |
,5714 |
,5753 |
|
0,2 |
,5793 |
,5832 |
,5871 |
,5910 |
,5948 |
,5987 |
,6026 |
,6064 |
,6103 |
,6141 |
|
0,3 |
,6179 |
,6217 |
,6255 |
,6293 |
,6331 |
,6368 |
,6406 |
,6443 |
,6480 |
,6517 |
|
0,4 |
,6554 |
,6591 |
,6628 |
,6664 |
,6700 |
,6736 |
,6772 |
,6808 |
,6844 |
,6879 |
|
0,5 |
,6915 |
,6950 |
,6985 |
,7019 |
,7054 |
,7088 |
,7123 |
,7157 |
,7190 |
,7224 |
|
0,6 |
,7257 |
,7291 |
,7324 |
,7357 |
,7389 |
,7422 |
,7454 |
,7486 |
,7517 |
,7549 |
|
0,7 |
,7580 |
,7611 |
,7642 |
,7673 |
,7703 |
,7734 |
,7764 |
,7794 |
,7823 |
,7852 |
|
0,8 |
,7881 |
,7910 |
,7939 |
,7967 |
,7995 |
,8023 |
,8051 |
,8078 |
,8106 |
,8133 |
|
0,9 |
,8159 |
,8186 |
,8212 |
,8238 |
,8264 |
,8289 |
,8315 |
,8340 |
,8365 |
,8389 |
|
1,0 |
,8413 |
,8438 |
,8641 |
,8485 |
,8508 |
,8531 |
,8554 |
,8577 |
,8599 |
,8621 |
|
1,1 |
,8643 |
,8665 |
,8686 |
,8708 |
,8729 |
,8749 |
,8770 |
,8790 |
,8810 |
,8830 |
|
1,2 |
,8849 |
,8869 |
,8888 |
,8907 |
,8925 |
,8944 |
,8962 |
,8980 |
,8997 |
,9015 |
|
1,3 |
,9032 |
,9049 |
,9066 |
,9082 |
,9099 |
,9115 |
,9131 |
,9147 |
,9162 |
,9177 |
|
1,4 |
,9192 |
,9207 |
,9222 |
,9236 |
,9251 |
,9265 |
,9279 |
,9292 |
,9306 |
,9319 |
|
1,5 |
,9332 |
,9345 |
,9357 |
,9370 |
,9382 |
,9394 |
,9406 |
,9418 |
,9429 |
,9441 |
|
1,6 |
,9452 |
,9463 |
,9474 |
,9484 |
,9495 |
,9505 |
,9515 |
,9525 |
,9535 |
,9545 |
|
1,7 |
,9554 |
,9564 |
,9573 |
,9582 |
,9591 |
,9599 |
,9608 |
,9616 |
,9625 |
,9633 |
|
1,8 |
,9641 |
,9649 |
,9656 |
,9664 |
,9671 |
,9678 |
,9686 |
,9693 |
,9699 |
,9706 |
|
1,9 |
,9713 |
,9719 |
,9726 |
,9732 |
,9738 |
,9744 |
,9750 |
,9756 |
,9761 |
,9767 |
|
2,0 |
,9772 |
,9778 |
,9783 |
,9788 |
,9793 |
,9798 |
,9803 |
,9808 |
,9812 |
,9817 |
|
2,1 |
,9821 |
,9826 |
,9830 |
,9834 |
,9838 |
,9842 |
,9846 |
,9850 |
,9854 |
,9857 |
|
2,2 |
,98в1 |
,9864 |
,9868 |
,9871 |
,9875 |
,9878 |
,9881 |
,9884 |
,9887 |
,9890 |
|
2,3 |
,9893 |
,9896 |
,9898 |
,9901 |
,9904 |
,9906 |
,9909 |
,9911 |
,9913 |
,9916 |
|
2,4 |
,9918 |
,9920 |
,9922 |
,9925 |
,9927 |
,9929 |
,9931 |
,9932 |
,9934 |
,9936 |
|
2,5 |
,9938 |
,9940 |
,9941 |
,9943 |
,9945 |
,9946 |
,9948 |
,9949 |
,9951 |
,9952 |
|
2,6 |
,9953 |
,9955 |
,9956 |
,9957 |
,9959 |
,9960 |
,9961 |
,9962 |
,9963 |
,9964 |
|
2,7 |
,9965 |
,9966 |
,9967 |
,9968 |
,9969 |
,9970 |
,9971 |
,9972 |
,9973 |
,9974 |
|
2,8 |
,9974 |
,9975 |
,9976 |
,9977 |
,9977 |
,9978 |
,9979 |
,9979 |
,9980 |
,9981 |
|
2,9 |
,9981 |
,9982 |
,9982 |
,9983 |
,9984 |
,9984 |
,9985 |
,9985 |
,9986 |
,9986 |
|
3,0 |
,9987 |
,9990 |
,9993 |
,9995 |
,9997 |
,9998 |
,9998 |
,9999 |
,9999 |
1,0000 |
2.1.1. При задании односторонних границ на контролируемый параметр искомый показатель вычисляют по формулам:
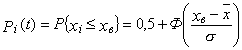 , (4)
, (4)
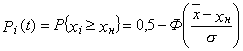 . (5)
. (5)
2.1.2. Нормальное распределение имеет место, как правило, у показателей, определяющих диаметральные и линейные размеры, полученные после обработки металла резанием, если погрешность настройки существенно меньше допуска на обработку или распределена по закону, близкому к нормальному.
В этом случае за х, s в формулах (1)-(3) следует принимать значения:
![]() ; (6)
; (6)
![]() , (7)
, (7)
где М(х), sx - математическое ожидание и среднее квадратическое отклонение мгновенной погрешности обработки;
М(х0), sн - математическое ожидание и среднее квадратическое отклонение погрешности настройки.
2.1.3. Если известны или определены по результатам анализа точности технологических процессов функции смещения центра группирования размеров mx(t) и изменения мгновенной погрешности, определяемой через среднее квадратическое отклонение sх(t), вероятность выполнения задания ТС вычисляют по выражению
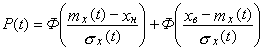 . (8)
. (8)
Выражения для расчета P(t) при различных функциях изменения mx(t) и sx(t) приведены в табл. 2.
Таблица 2
|
Функция изменения mx(t) и sx(t) |
Выражение для расчета вероятности выполнения задания |
|
mx(t)=m0=const |
|
|
sx(t)=s0=const |
|
|
mx(t)=m0+Dmt |
|
|
sx(t)=s0=const |
|
|
mx(t)=m0+Dmt |
|
|
sx(t)=s0+Dst |
|
|
mx(t)=m0-Dmt |
|
|
sx(t)=s0+Dst |
|
|
mx(t)=m0+Dmtn1 |
|
|
sx(t)=s0+Dstn2 |
|
|
mx(t)=m0=const |
|
|
sx(t)=s0t |
За m0 и s0 следует принимать, соответственно, среднее значение начального уровня настройки и начальное значение среднего квадратического отклонения.
2.2. Вероятность выполнения задания на основе закона распределения модуля разности следует рассчитывать в тех случаях, когда исследуемым параметром является случайная величина.
r=|x1-x2|, (9)
где x1, x2 - нормально распределенные независимые случайные
величины со средними значениями ![]() , и
, и ![]() и дисперсией
и дисперсией ![]() .
.
2.2.1. Закону распределения модуля разности может подчиняться распределение следующих параметров:
отклонение от симметричности поверхностей, имеющих общую ось или плоскость симметрии;
отклонение от параллельности осей в общей плоскости двух цилиндрических поверхностей;
отклонение от параллельности оси цилиндрической поверхности до базовой поверхности;
отклонение от параллельности поверхностей при симметрии последних относительно собственной оси или плоскости симметрии до базовой плоскости (расстояние определяется в фиксированной плоскости, перпендикулярной осям или плоскостям симметрии);
отклонение от параллельности осей цилиндрических плоскостей;
отклонение от параллельности двух плоскостей, номинально параллельных оси, и отклонение от параллельности оси и плоскости;
отклонение от перпендикулярности двух осей;
отклонение от пересечения осей (номинально пересекающихся);
отклонение угла наклона оси в фиксированной плоскости без учета отклонений;
отклонение от круглости (овальность, огранность и т.п.), определяемое как наибольшее расстояние от точек реальной поверхности до прилегающей окружности;
радиальное биение, измеренное в одном определенном торцевом сечении.
2.2.2. Вероятность выполнения задания по i-му параметру качества изготовляемой продукции в рассматриваемом случае определяют по формуле
Pi(t)=F(xв)-F(xн), (10)
где
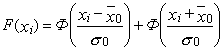 ; (11)
; (11)
![]() .
.
2.3. Закон Релея имеет место, если контролируемый параметр представляется в виде
![]() , (12)
, (12)
где X1, X2 - нормально распределенные независимые случайные
величины со средними ![]() и дисперсия s1 и s2
соответственно.
и дисперсия s1 и s2
соответственно.
2.3.1. Распределение Релея может иметь место для следующих параметров:
несоосность двух номинально соосных цилиндрических поверхностей (эксцентриситет, биение и т.д.);
непараллельность образующих двух цилиндрических поверхностей (конусность), если плоскость не фиксирована;
непараллельность двух плоскостей;
неперпендикулярность двух плоскостей или оси к плоскости;
разностенность (направление не задано).
2.3.2. Вероятность выполнения задания в рассматриваемом случае определяют по формуле
![]() , (13)
, (13)
где
![]() , (14)
, (14)
3. В общем случае вероятность выполнения задания по i-му параметру качества изготовляемой продукции за установленную наработку ty определяют по формуле
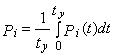 . (15)
. (15)
3.1. Если в процессе обработки мгновенное распределение контролируемого параметра не изменяется во времени, искомый показатель следует рассчитывать по выражениям, приведенным в пп. 2.1-2.3.
3.2. Если мгновенное распределение контролируемого параметра подчиняется нормальному закону, его дисперсия не изменяется во времени, а среднее значение (центр группирования) имеет вид
![]() , (16)
, (16)
искомый показатель вычисляют по формуле
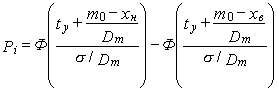 . (17)
. (17)
3.3. Если мгновенное распределение контролируемого параметра подчиняется нормальному закону, его дисперсия не изменяется во времени, а центр группирования имеет вид:
![]() , (18)
, (18)
искомый показатель вычисляют по формуле
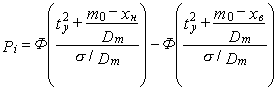 . (19)
. (19)
3.4. В случае нормального распределения контролируемого параметра при постоянном центре группирования х0 и при линейной зависимости величины мгновенного рассеяния от времени обработки
s0(t)= s0+2lt, (20)
где
![]() ;
;
smax, s0 - соответственно, максимальное и начальное значения величины среднего квадратического отклонения контролируемого параметра, искомый показатель вычисляют по формуле
Pi=F(z1l)-F(z2l), (21)
где
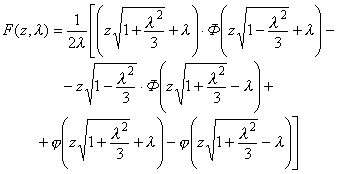 ; (22)
; (22)
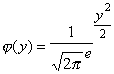 ; (23)
; (23)
![]() ; (24)
; (24)
![]() ; (25)
; (25)
![]()
Значения функции F(z, l) приведены в табл. 3.
Таблица 3
|
z |
F (z, l) при l |
z |
F (z, l) при l |
||||||
|
3 |
6 |
10 |
25 |
3 |
6 |
10 |
25 |
||
|
0,00 |
0,0000 |
0,0000 |
0,0000 |
0,0000 |
1,00 |
0,3194 |
0,3002 |
0,2930 |
0,2894 |
|
0,05 |
0,0166 |
0,0150 |
0,0146 |
0,0145 |
1,05 |
0,3333 |
0,3151 |
0,3076 |
0,3028 |
|
0,10 |
0,0332 |
0,0304 |
0,0293 |
0,0289 |
1,10 |
0,3466 |
0,3299 |
0,3223 |
0,3188 |
|
0,15 |
0,0498 |
0,0451 |
0,0433 |
0,0434 |
1,15 |
0,3595 |
0,3445 |
0,3369 |
0,3328 |
|
0,20 |
0,0664 |
0,0601 |
0,0586 |
0,0579 |
1,20 |
0,3719 |
0,3589 |
0,3515 |
0,3472 |
|
0,25 |
0,0830 |
0,0751 |
0,0732 |
0,0723 |
1,25 |
0,3837 |
0,3731 |
0,3662 |
0,3617 |
|
0,30 |
0,0995 |
0,0901 |
0,0879 |
0,0868 |
1,30 |
0,3949 |
0,3869 |
0,3807 |
0,3762 |
|
0,35 |
0,1161 |
0,1052 |
0,1025 |
0,1013 |
1,35 |
0,4055 |
0,4003 |
0,4952 |
0,4906 |
|
0,40 |
0,1325 |
0,1202 |
0,1172 |
0,1157 |
1,40 |
0,4155 |
0,4130 |
0,4094 |
0,4051 |
|
0,45 |
0,1489 |
0,1352 |
0,1318 |
0,1302 |
1,45 |
0,4248 |
0,4251 |
0,4254 |
0,4196 |
|
0,50 |
0,1652 |
0,1502 |
0,1464 |
0,1447 |
1,50 |
0,4335 |
0,4364 |
0,4367 |
0,4340 |
|
0,55 |
0,1815 |
0,1653 |
0,1611 |
0,1592 |
1,55 |
0,4415 |
0,4468 |
0,4192 |
0,4485 |
|
0,60 |
0,1976 |
0,1803 |
0,1758 |
0,1736 |
1,60 |
0,4489 |
0,4562 |
0,4607 |
0,4627 |
|
0,65 |
0,2136 |
0,1953 |
0,1994 |
0,1881 |
1,65 |
0,4555 |
0,4646 |
0,4707 |
0,4762 |
|
0,70 |
0,2295 |
0,2103 |
0,2051 |
0,2026 |
1,70 |
0,4616 |
0,4719 |
0,4891 |
0,4873 |
|
0,75 |
0,2495 |
0,2253 |
0,2197 |
0,2170 |
1,75 |
0,4670 |
0,4781 |
0,4558 |
0,4948 |
|
0,80 |
0,2605 |
0,2403 |
0,2344 |
0,2315 |
1,80 |
0,4719 |
0,4833 |
0,4908 |
0,4985 |
|
0,85 |
0,2787 |
0,2554 |
0,2490 |
0,2460 |
1,85 |
0,4762 |
0,4875 |
0,4844 |
0,4997 |
|
0,90 |
0,2906 |
0,2703 |
0,2637 |
0,2604 |
1,90 |
0,4800 |
0,4908 |
0,4992 |
0,5000 |
|
0,95 |
0,3032 |
0,2853 |
0,2749 |
0,2749 |
1,95 |
0,4833 |
0,4535 |
0,4983 |
|
3.5. Если мгновенное распределение контролируемого параметра подчиняется закону Релея с параметром s0(t), который изменяется по линейному закону
s0(t)=s0+Kt·t, (26)
искомый показатель Pi рассчитывают по формуле
![]() . (27)
. (27)
4. Пример. Для операции резания на автомате
продольного точения погрешность обработки детали по диаметру ![]() задана в виде суммы
нормально распределенной погрешности настройки с параметрами m=10 мм, s=0,002 мм и смещения центра группирования по линейному
закону со скоростью u=0,002
мм/ч.
задана в виде суммы
нормально распределенной погрешности настройки с параметрами m=10 мм, s=0,002 мм и смещения центра группирования по линейному
закону со скоростью u=0,002
мм/ч.
Определить вероятность выполнения задания P(t) по указанному диаметру для момента времени t=3 ч.
4.1. По условию задачи плотность распределения погрешности обработки имеет вид
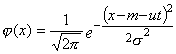 .
.
4.2. Подставляем искомую вероятность согласно выражению (1) в виде
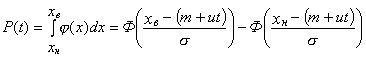 ,
,
где 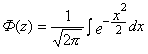 - функция нормального
распределения.
- функция нормального
распределения.
4.3. Подставляем в последнее выражение верхнее предельное значение хв=10,01 мм, нижнее предельное значение хн=9,955 мм и параметры m, s и u из условия задачи:
![]() .
.
ПРИЛОЖЕНИЕ 7
Справочное
РАСЧЕТНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ ВЫПОЛНЕНИЯ ЗАДАНИЯ ПО ПАРАМЕТРАМ КАЧЕСТВА ИЗГОТОВЛЯЕМОЙ ПРОДУКЦИИ ДЛЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
1. Определение показателей выполнения заданий по параметрам качества изготовляемой продукции для ТС технологического процесса расчетными методами производится по результатам оценки аналогичных показателей для ТС технологических операций.
2. При независимости погрешностей обработки на последовательно выполняемых операциях технологического процесса, показатели выполнения заданий по r-му параметру качества изготовляемой продукции, следует определять по формуле
![]() , (1)
, (1)
где ![]() - соответствующий
показатель выполнения задания по r-му
параметру качества изготовляемой продукции для i-й технологической операции;
- соответствующий
показатель выполнения задания по r-му
параметру качества изготовляемой продукции для i-й технологической операции;
n - количество операций, выполняемых по данному технологическому процессу.
3. При независимости между погрешностями обработки на двух операциях (черт. 1) вероятность выполнения задания по одному r-му параметру качества изготовляемой продукции вычисляют по формуле
![]()
где ![]() ,
, ![]() - соответственно,
вероятность выполнения задания по r-му
параметру для первой и для второй операций;
- соответственно,
вероятность выполнения задания по r-му
параметру для первой и для второй операций;
Kпд(1, К; 2, К) - коэффициент передачи дефекта с первой операции на вторую по r-му параметру.
Коэффициент передачи дефекта характеризует стохастическую связь между погрешностями обработки на двух операциях и позволяет оценить практическую значимость и необходимость учета этой связи в расчетах надежности (в отличие от коэффициента корреляции между погрешностями, знание которого не достаточно для оценки вероятности «переноса» дефекта с предыдущей операцию на последующую).
3.1. В общем случае коэффициент передачи дефекта с первой операции по l-му параметру на вторую по r-му параметру определяют по опытно-статистическим данным по формуле
![]() , (3)
, (3)
где n - количество изготовленных единиц продукции, проверенных после первой операции по l-му параметру и после второй операции по r-му параметру;
d(1, l;) - количество единиц продукции, дефектных по l-му параметру после первой операции;
d(2, К)- количество единиц продукции, дефектных по r-му параметру после второй операции;
d(1, l; 2, К) - количество единиц продукции, дефектных по l-му параметру после первой операции и имеющих дефект по r-му параметру после второй операции.
Если Kпд(1, К; 2, K)=0, то выражение (2) принимает вид
![]() .
.
Если Kпд(1, К; 2, K)=0, то выражение (2) принимает вид
![]() .
.
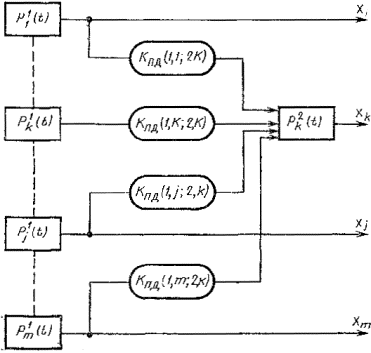
Черт. 2
4. При зависимости между погрешностями обработки на двух операциях по m параметрам качества изготовляемой продукции (см. черт. 2) искомый показатель по r-му параметру вычисляют по формуле
5. При зависимости между погрешностями обработки на n последовательно выполняемых операциях по m параметрам качества изготовляемой продукции искомый показатель вычисляют по рекурентной формуле
![]() ; (5)
; (5)
![]() ;
;
![]() ;
;
![]() для i=1…m.
для i=1…m.
6. При проведении расчетов по пп. 2-5 показатели выполнения задания по качеству для технологических операций должны быть заданы с учетом возможной отбраковки дефектных деталей в процессе операционного контроля, т.е. распределение контролируемого параметра х на выходе ТС операции обработки следует рассматривать после завершения контрольной операции, а вероятность выполнения задания по j-му параметру качества продукции на рассматриваемой операции вычисляют по формуле
Pj(t)=1-Pj, 0(t)dj(t)-[1-Pj, 0(t)]bj(t),
где Рj0(t) - вероятность выполнения задания по j-му параметру качества при отсутствии контрольной операции;
dj(t); bj(t) - соответственно риск поставщика и риск потребителя, определяемые по ГОСТ 15895-77.
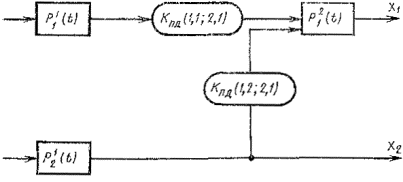
Черт. 3
Пример. Определить вероятность выполнения задания на токарной операции 2 (чистовая обработка) по диаметру x1, с учетом передачи дефектов по диаметрам x1 и x2 с операции 1 (черновая обработка) в соответствии с черт. 3.
Исходные данные:
![]() ,
,
Kпд(1,1; 2,1)=0,32; Kпд(1,2; 2,1)=0,4.
Определяем искомый показатель по формуле (4):
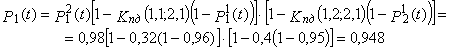 .
.
ПРИЛОЖЕНИЕ 8
Справочное
ОПЫТНО-СТАТИСТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ ВЫПОЛНЕНИЯ ЗАДАНИЙ ПО ПАРАМЕТРАМ КАЧЕСТВА ИЗГОТОВЛЯЕМОЙ ПРОДУКЦИИ
1. В общем случае оценку вероятности выполнения задания по одному (j-му) или одновременно по n параметрам качества опытно-статистическими методами следует производить по результатам выборочного обследования N единиц изготовленной продукции по формулам:
где dj(t) - количество дефектных по i-му параметру единиц продукции;
d(t) - количество дефектных, хотя бы по одному из n контролируемых параметров.
2. Оценку дисперсии оценки искомого показателя производят по формуле
![]() ,
,
где Р - оценка искомого показателя, рассчитанная по формуле (1) или (2)
3. Если общее количество измеренных единиц продукции не превосходит 10% от объема всей изготовленной продукции (за рассматриваемый промежуток времени) и значение искомого показателя надежности Р не менее 0,9, доверительные границы имеют вид
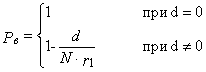
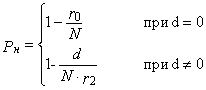
где d - количество обнаруженных дефектных единиц продукции (по рассматриваемым показателям качества);
Рв, Pн - верхняя и нижняя доверительные границы оцениваемого показателя;
r0, r1, r2 - коэффициенты, определяемые по ГОСТ 11.005-74 (табл. 2, 6 и 7) в зависимости от числа дефектных единиц m=d и доверительной вероятности g.
4. Пример. В результате проведения выборочного обследования сборочного участка из ста проверенных изделий восемь имели отклонения от установленных требований к качеству сборки.
Определить вероятность выполнения задания сборочным участком по параметрам качества изготовляемой продукции и ее доверительные границы при доверительной вероятности g=0,95.
4.1. Определяем искомую вероятность по п. 1:
![]() .
.
Определяем дисперсию величины Р по п. 2.
![]() ,
,
4.3. Определяем доверительные границы Рв и Рн по п. 3 при доверительной вероятности g=0,95.
![]() ;
;
![]() .
.
ПРИЛОЖЕНИЕ 9
Справочное
РЕГИСТРАЦИОННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ ВЫПОЛНЕНИЯ ЗАДАНИЙ ПО ПАРАМЕТРАМ КАЧЕСТВА ИЗГОТОВЛЯЕМОЙ ПРОДУКЦИИ
1. В общем случае оценку вероятности выполнения задания по одному или нескольким параметрам качества изготовляемой продукции регистрационными методами следует производить по формуле
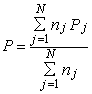 , (1)
, (1)
где Рj - оценка искомого показателя Р по информации, содержащейся в событии Aj;
nj - объем изготовленной продукции, соответствующей событию Aj;
N - число событий Aj.
2. Если известна плотность априорного распределения искомого показателя. fp(x) (полученное, например, расчетным методом), то величину Pj следует определять по формуле
где Р(Аj/х) - условная вероятность появления события Aj при условии, что Р=х.
3 Если произошло событие Аj и известна зависимость вероятности его появления как функции от искомого показателя Р, L(P) (функция правдоподобия), то величину Рj, следует определять по методу максимального правдоподобия из уравнения
3.1. Если событие Aj представляет собой забракование m из n изготовленных изделий, а искомым показателем Р является вероятность выполнения задания по качеству, функция правдоподобия имеет вид
![]() .
.
При этом Pj следует определять в соответствии с выражением (3) по формуле
![]() .
.
3.2. Если событие Аj представляет собой приемку партий готовой продукции из общего числа М партий, причем каждая партия подвергалась статистическому контролю и принималась при отсутствии дефектных единиц в выборке, а искомым показателем Р является вероятность выполнения задания по качеству, функция правдоподобия имеет вид:
![]() ,
,
где n - объем контрольной выборки.
При этом величину Р следует определять в соответствии с выражением (3) по формуле
![]() .
.
4. Если регистрируемое событие Аj представляет собой результат статистического приемочного контроля, вероятность выполнения задания по j-му (одному) или по n (одновременно нескольким) параметром качества изготовляемой продукции следует определять по формуле
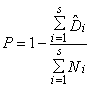 ,
,
где ![]() - оценка числа
дефектных (соответственно, только по j-му или по любому из параметров) единиц продукции в i-й партии;
- оценка числа
дефектных (соответственно, только по j-му или по любому из параметров) единиц продукции в i-й партии;
Ni - объем i-й партии продукции;
s - количество партий, поступивших на контроль за рассматриваемый промежуток времени.
При этом дисперсия оценки искомого показателя имеет вид
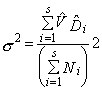 ,
,
где ![]() - дисперсия оценки
числа дефектных единиц продукции в партии.
- дисперсия оценки
числа дефектных единиц продукции в партии.
Значения ![]() и
и ![]() определяют в
зависимости от плана приемочного контроля и его результатов.
определяют в
зависимости от плана приемочного контроля и его результатов.
4.1. При одноступенчатом контроле без последующей разбраковки его план П (n, с) характеризуется объемом выборки и приемочным числом с (с<n), а по результату контроля выборки партия объемом N принимается, если число дефектных изделий в выборке у с, и забраковывается, если у>с. Результатом контроля партии являются обнаруженные в партии число дефектных изделии Y=y и число годных изделий х=n-у.
В этом случае оценки для числа предъявленных дефектных
изделий ![]() и дисперсии
и дисперсии ![]() равны
равны
![]() ; (4)
; (4)
![]() . (5)
. (5)
4.2. При одноступенчатом контроле с разбраковкой его план П (n, с) характеризуется объемом выборки n и приемочным числом с, а по результату контроля выборки партия объемом N принимается, если число дефектных изделий в выборке y£c, и подвергается сплошному контролю, если y>с. Результатом контроля партии являются обнаруженные в партии число дефектных изделий Y и число годных изделий X, причем
![]()
![]()
где D - число дефектных изделий в партии, обнаруженных при сплошном контроле
B этом случае оценки ![]() и
и ![]() принимают вид:
принимают вид:
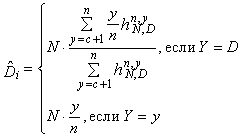 .
.
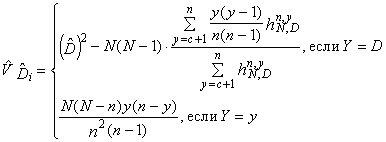 ,
,
где ![]() - гипергеометрическая
вероятность, вычисляемая по формуле
- гипергеометрическая
вероятность, вычисляемая по формуле
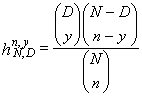 . (6)
. (6)
5. При одноступенчатом контроле с последующим сплошным контролем план контроля П (n, с) характеризуется объемом выборки n и приемочным числом с, а по результату контроля выборки партия объемом N подвергается сплошному контролю, если число дефектных изделий в выборке у£с, и забраковывается, если у>с. Результатом контроля партии являются обнаруженные в партии число дефектных изделий Y и число годных изделий X, причем
![]()
![]() ,
,
где D - число дефектных изделий в контролируемой партии.
В этом случае оценки ![]() и
и ![]() могут быть вычислены
по формулам:
могут быть вычислены
по формулам:
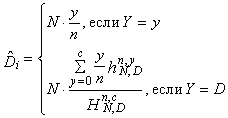 . (7)
. (7)
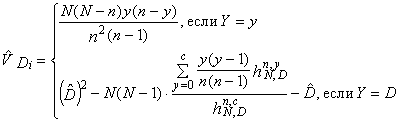
где ![]() .
.
6. При одноступенчатом контроле с условной разбраковкой план контроля П (n, с, c1) характеризуется объемом случайной выборки n, приемочным и браковочным числами с, c1 (с<c1<n), а по результату контроля выборки партия объемом N принимается, если число дефектных изделий в выборке y£c, подвергается сплошному контролю, если с<у<с1, и забраковывается, если в партии число дефектных изделий y£c1. Результаты контроля партии являются обнаруженные в партии число дефектных деталей Y и число годных изделий X, причем:
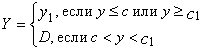 .
.
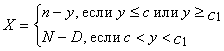 .
.
В этом случае ![]() и
и ![]() имеют вид:
имеют вид:
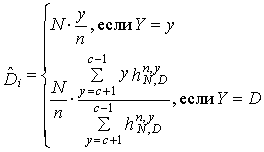
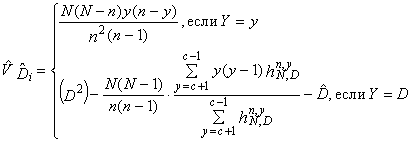
7. Пример. В процессе выборочного приемочного контроля одна из трех партий деталей, прошедших термическую обработку, была забракована.
Партия принималась в случае, если в выборке объема n=5 не было ни одной дефектной детали и браковалась в противном случае. Объем партии N=1000 шт.
Определить вероятность выполнения задания Р по параметрам качества продукции, если известно, что эта величина лежит в пределах
0,956 £ Р £ 1.
7.1. Из условия задачи задаемся априорной плотностью распределения величины Р:
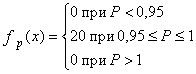
7.2. Представляем искомую вероятность согласно выражению (2) в виде
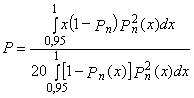
где Рn(х) - вероятность приемки партии при фиксированном значении Р=х.
7.3. Подставляя в последнюю формулу выражение вероятности приемки Рn(х) для заданного плана контроля в случае N³nPn(x)=x5 будем иметь
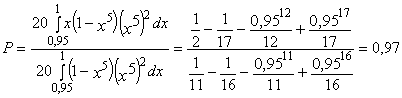 .
.
СОДЕРЖАНИЕ
Приложение 1 справочное Определение поля рассеяния контролируемого параметра. 8
Приложение 3 справочное Оценка точности технологической системы методом квалитетов. 15
Приложение 4 справочное Расчетные методы определения показателей точности технологических систем.. 15
Приложение 5 справочное Опытно-статистические методы оценки точности технологических систем.. 21
Приложение 6 справочное Расчетные методы определения показателей выполнения заданий по параметрам качества изготовляемой продукции для технологических операций. 26
Приложение 7 справочное Расчетные методы определения показателей выполнения задания по параметрам качества изготовляемой продукции для технологических процессов. 32
Приложение 8 справочное Опытно-статистические методы определения показателей выполнения заданий по параметрам качества изготовляемой продукции. 34
Приложение 9 справочное Регистрационные методы определения показателей выполнения заданий по параметрам качества изготовляемой продукции. 36
| Расположен в: |
|---|
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/7743
На эту страницу сайта можно сделать ссылку:
На правах рекламы:
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|