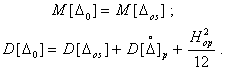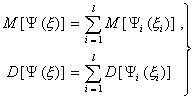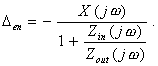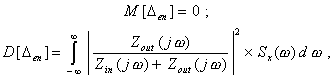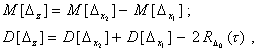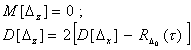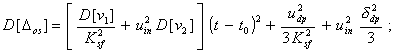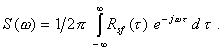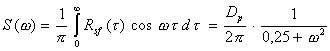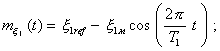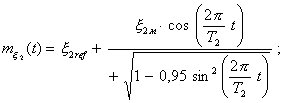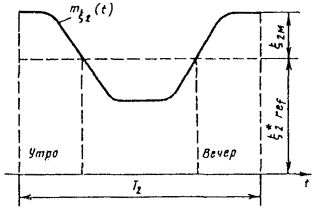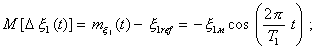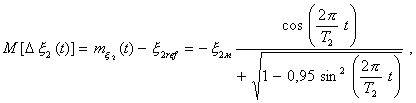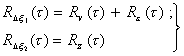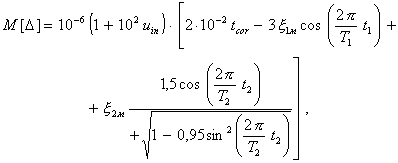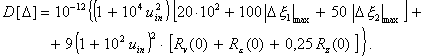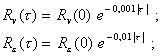
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"Методический материал по применению ГОСТ 8.009-84 "ГСИ. Нормируемые метрологические характеристики средств измерений".МЕТОДИЧЕСКИЙ МАТЕРИАЛ «ГСИ. НОРМИРУЕМЫЕ МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ» Цель методического материала - разъяснение положений ГОСТ 8.009-84 и рассмотрение ряда практических вопросов, связанных с его применением. 1. НЕОБХОДИМОСТЬ РАЗРАБОТКИ СИСТЕМЫ НОРМИРОВАНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ. ТРЕБОВАНИЯ К НОРМИРОВАННЫМ МЕТРОЛОГИЧЕСКИМ ХАРАКТЕРИСТИКАМ СРЕДСТВ ИЗМЕРЕНИЙ.Развитие науки и техники, повышение требований к качеству продукции и эффективности производства привели к радикальному изменению требований к измерениям. Один из основных аспектов этих требований - обеспечение возможности достаточно достоверной оценки погрешности измерений. Отсутствие данных о точности измерений или недостаточно достоверные ее оценки полностью или в значительной степени обесценивают информацию о свойствах объектов и процессов, качестве продукции, об эффективности технологических процессов, о количестве сырья, продукции и т. п., получаемую в результате измерений. Некорректная оценка погрешности измерений чревата большими экономическими потерями, а иногда и техническими последствиями. Заниженная оценка погрешности измерений ведет к увеличению брака продукции, неэкономичному или неправильному учету расходования материальных ресурсов, неправильным выводам при научных исследованиях, ошибочным решениям при разработке и испытаниях образцов новой техники. Завышенная оценка погрешности измерений, следствием чего, как правило, является ошибочный вывод о необходимости применения более точных средств измерений (СИ), вызывает непроизводительные затраты на разработку, промышленный выпуск и эксплуатацию СИ. Стремление максимально приблизить оценку погрешности измерений к ее действительному значению так, чтобы она при этом оставалась в вероятностном смысле «оценкой сверху», - одна из характерных тенденций развития современной практической метрологии. Эта тенденция приобретает особенно большое практическое значение там, где требуемая точность измерений приближается к точности, которую могут обеспечивать образцовые СИ и где повышение корректности оценок точности измерений по существу является одним из резервов повышения точности измерений. Погрешность измерений обусловлена, в общем случае, рядом факторов. Она зависит от свойств применяемых СИ, способов использования СИ (методик выполнения измерений), правильности калибровки и поверки СИ, условий, в которых производятся измерения, скорости (частоты) изменения измеряемых величин, алгоритмов вычислений, погрешности, вносимой оператором, и др. Следовательно, задача оценки погрешности измерений в современных условиях, в частности, технических измерений - сложная комплексная задача. В соответствии с назначением ГОСТ 8.009-84 в настоящем методическом материале рассматриваются только те проблемы, которые связаны с составляющей погрешности измерений, обусловленной свойствами применяемых СИ. Эта составляющая названа инструментальной составляющей погрешности измерений. При подготовке к измерениям, при проектировании различных процессов (например, технологических процессов производства, процессов контроля качества продукции и др.), в которых используются измерения, необходимо обращать внимание не только на выбор СИ и связанную с ними инструментальную составляющую погрешности измерений, но и на другие факторы, влияющие на погрешность измерений. Только тогда сможет быть достигнута конечная цель - высокое качество измерений, требуемая точность измерений. Инструментальная составляющая погрешности измерений состоит, в свою очередь, из ряда составляющих, обусловленных собственными свойствами элементов и материалов, используемых в СИ; реакцией СИ на изменения влияющих величин и на скорость (частоту) изменения измеряемых величин; воздействие СИ на объект измерений; способностью СИ различать малые изменения измеряемых величин во времени или в пространстве (разрешающая способность) и т. п. Для современной измерительной техники характерно усложнение условий эксплуатации и повышение скорости изменения измеряемых процессов. Изменяющиеся внешние воздействия со стороны окружающей среды и изменяющиеся воздействия на вход СИ во многих случаях становятся факторами, вносящими основной вклад в погрешность измерений. В этих случаях оценка инструментальной составляющей погрешности измерений оказывается весьма сложной. Она может производиться только на основании информации о свойствах СИ, характере изменений измеряемых величин, некоторых свойствах объекта измерений, определяющих реакцию объекта измерений на подключение к нему СИ. Основное необходимое условие оценки инструментальной составляющей погрешности измерений - информация о свойствах СИ, влияющих на результаты и погрешности измерений, т. е. информация о метрологических характеристиках (MX) СИ. Эта информация используется не только для оценки инструментальной составляющей погрешностей измерений. На ее основе решается и ряд других задач, связанных с применением СИ. Основными задачами, решаемыми с использованием данных о MX СИ, являются следующие: 1. Оценка инструментальной составляющей погрешности измерений. Специфика ее в том, что погрешность, особенно для технических измерений, следует оценивать до проведения измерений, на стадии проектирования измерительных процессов. При этом должны учитываться не только MX СИ, но и все другие факторы, влияющие на инструментальную составляющую погрешности измерений: изменения влияющих величин (температуры окружающей среды, напряжения питания, воздействия электромагнитных полей и других неинформативных параметров входного сигнала), свойства объекта измерений, скорость (частота) изменения измеряемых величин, входные свойства устройств, подключаемых к выходу СИ, выходные свойства устройств (первичных или промежуточных измерительных преобразователей), к выходу которых подключается СИ, и др. Примечание. При оценке погрешности измерений необходимо помнить о том, что кроме инструментальной составляющей, имеются еще другие составляющие погрешности измерений. Поэтому при решении любых задач, связанных с погрешностями измерений, нельзя ограничиваться оценкой только их инструментальных составляющих, следует учитывать и все другие составляющие, вносящие заметный вклад в погрешность измерений. 2. Выбор СИ, MX которых обеспечивали бы требуемое качество измерений при известных условиях применения СИ. Эта задача в известной мере является обратной по отношению к задаче оценки инструментальной составляющей погрешности измерений. 3. Сравнение СИ различных типов по MX. Необходимость решения этой задачи возникает на стадии как разработки, так и эксплуатации СИ. Решают ее, как правило, с учетом условий применения СИ, которые в большей или меньшей степени известны. При разработке СИ обычно известны лишь граничные условия их применения, в то время как внутренняя структура этих условий (законы изменения воздействующих факторов) большей частью остается неизвестной. В этом случае MX СИ, по существу, - единственные исходные данные для построения критериев сравнения. 4. Разработка сложных измерительных систем (ИС). Обоснованная разработка ИС связана с необходимостью выбора отдельных компонентов, входящих в ИС, исходя из требований, предъявляемых к ИС в целом. Одно и то же требование к ИС может быть удовлетворено при различном соотношении MX измерительных устройств, ее комплектующих. Очевидно, что «распределение требований» между отдельными компонентами ИС должно быть технически и экономически целесообразным. MX СИ должны позволять обоснованно решать и эту задачу. 5. Оценка погрешности ИС. Для успешности наладки и эксплуатации ИС необходимо знать, с какой погрешностью измеряется или преобразуется соответствующая величина. В большинстве случаев определение погрешности сложных систем экспериментальным путем сопряжено с большими трудностями, а иногда практически невозможно, поскольку отдельные компоненты ИС могут работать в отличающихся друг от друга и случайно изменяющихся внешних условиях. Бывает целесообразно, а нередко и единственно возможно, решать эту задачу расчетным путем, принимая за исходные данные MX СИ, образующих систему. При проектировании ИС, когда они еще не смонтированы, также необходимо оценивать предполагаемые погрешности ИС. Здесь оценка погрешности ИС может быть получена только расчетным путем на основе MX компонентов ИС. Основное условие возможности решения всех указанных задач - наличие связи между MX СИ и инструментальными составляющими погрешностей измерений или погрешностями ИС. Сведения о MX СИ, как правило, получают из нормативно-технических документов (НТД) на СИ. Лишь в случаях, когда данных о нормированных типовых MX недостаточно для эффективного использования СИ, экспериментально исследуют конкретные экземпляры СИ с целью определения их индивидуальных MX. Очевидно, что этот путь определения MX СИ является исключительным, возможным лишь в редких случаях. Из изложенного следует исключительная важность номенклатуры и способов выражения нормированных метрологических характеристик (НМХ). Этими характеристиками пользуются потребители СИ и измерительной информации, разработчики СИ, ИС, систем автоматического управления, проектировщики производственных процессов (измерительных процессов и процессов управления). Из рассмотрения задач можно сделать вывод о противоречивости вытекающих из них требований к НМХ СИ. Для решения 1 и 2-й задач наиболее целесообразно, чтобы метрологические свойства СИ были описаны одной комплексной НМХ, позволяющей непосредственно определять инструментальную составляющую погрешности измерений. Для решения 3 и 4-й задач целесообразно, чтобы метрологические свойства СИ были описаны комплексом НМХ, каждая из которых определяла бы одно существенное с метрологической точки зрения свойство СИ. При этом весь комплекс НМХ должен содержать исчерпывающие характеристики всех метрологических свойств СИ и каждая из НМХ должна, по возможности, отражать определенное физическое свойство СИ, с целью облегчения решения 3-й задачи. При дифференцированном нормировании MX для решения 1, 2, 4, 5-й задач должны быть выполнены следующие условия: между НМХ и инструментальной составляющей погрешности измерений должна быть установлена определенная связь, учитывающая другие характеристики измерительного процесса; НМХ СИ должны быть такими, чтобы можно было установить связь между ними и MX ИС, представляющих собой комбинацию различных СИ. Кроме того должна быть обеспечена практическая возможность достаточно простого контроля СИ на соответствие НМХ. В случае нормирования одной комплексной MX, отражающей все метрологические свойства СИ, контроль СИ будет весьма сложным, да и сама возможность установления такой MX вызывает сомнение. В случае нормирования комплекса MX, каждая из которых отражает одно определенное физическое свойство СИ, контроль может быть более простым, и его результаты позволят делать выводы не только о соответствии СИ нормам, но в случае отрицательных результатов и о причинах неисправности СИ. Вместе с тем необходимо учитывать, что при таком нормировании может оказаться, что количество контролируемых характеристик будет достаточно велико и трудоемкость контроля может оказаться существенной. Изложенные соображения приводят к выводу, что целесообразно нормировать комплекс MX, который, с одной стороны, не должен быть чрезмерно большим, а с другой - каждая из НМХ должна отражать конкретные физические свойства СИ. НМХ должны быть выражены в такой форме, чтобы по ним можно было обоснованно решать изложенные выше задачи и одновременно достаточно просто осуществлять контроль СИ на соответствие НМХ. Характерной особенностью современной измерительной техники и техники управления является широкое распространение измерительных процессов, в которых одновременно участвуют СИ разных физических величин, основанные на разных принципах действия. Это вызывает необходимость построения методов нормирования MX СИ разных принципов действия и различного назначения на единой принципиальной основе. Поскольку НМХ СИ используются при оценках инструментальных составляющих погрешности измерений, проводимых в различных условиях, при сравнении между собой различных СИ в этих же условиях применения, при контроле качества СИ и т. п. НМХ должны отражать свойства только самого СИ, т. е. должны быть инвариантны к условиям применения и режиму работы СИ. При рассмотрении требований к НМХ необходимо учитывать, что метрологические свойства экземпляра СИ определенного типа отличаются от метрологических свойств всей совокупности СИ данного типа. Например, для данного экземпляра СИ систематическая погрешность - детерминированная величина, а для всей совокупности СИ данного типа - случайная величина, меняющаяся от экземпляра к экземпляру СИ. Из перечисленных выше задач, для решения которых используют НМХ СИ, основными являются оценка инструментальной составляющей погрешности измерений и выбор СИ. Решение этих задач основано на взаимосвязи между инструментальной составляющей погрешности измерений и НМХ СИ с учетом характеристик влияющих величин, отражающих условия эксплуатации СИ, и характеристик входного сигнала СИ, обусловливающих режим работы СИ. Характерной особенностью этой взаимосвязи является то, что инструментальная составляющая погрешности измерений, в свою очередь, содержит ряд составляющих, каждая из которых обусловливается определенными метрологическими свойствами СИ. Таким образом, инструментальная составляющая погрешности измерений может быть определена лишь как сумма (объединение) определенных составляющих. Типичными для общего случая являются четыре составляющие погрешности измерений, обусловленные свойствами СИ, т. е. четыре составляющие инструментальной составляющей погрешности измерений: 1) погрешность обусловленная неидеальностью собственных свойств СИ, т. е. отличием действительной функции преобразования СИ в нормальных условиях от номинальной функции преобразования или для меры, обусловленная отличием действительного значения выходной величины меры в нормальных условиях от номинального значения этой величины. Эта составляющая называется основной погрешностью СИ; 2) погрешность, обусловленная реакцией СИ на изменения внешних влияющих величин и неинформативных параметров входного сигнала относительно их нормальных значений. Эта составляющая зависит как от свойств СИ, так и от изменений влияющих величин, она называется дополнительной погрешностью СИ; 3) погрешность, обусловленная реакцией СИ на скорость (частоту) изменения входного сигнала. Эта составляющая, определяющая динамическую погрешность измерений, зависит как от динамических свойств СИ, так и от частотного спектра входного сигнала, она называется динамической погрешностью СИ. Примечание. Режим измерений, при котором динамическая составляющая погрешности измерений вносит заметный вклад в общую погрешность измерений, является динамическим режимом измерений. Таким образом, режим измерений (статический или динамический) определяется соотношением между скоростью изменения входного сигнала и динамическими свойствами СИ; 4) погрешность, обусловленная взаимодействием СИ и объекта измерений. Подключение СИ к объекту измерений во многих случаях приводит к изменению значения измеряемой величины относительно того значения, которое имела измеряемая величина до подключения СИ к объекту измерений и определение которого является целью измерений. Эта составляющая зависит от свойств как СИ, так и объекта измерений. Первые две составляющие представляют собой статическую погрешность СИ. Третья составляющая представляет собой динамическую погрешность СИ. Выделение статической и динамической погрешностей СИ, как суммируемых составляющих, допустимо не всегда. В общем случае при измерении изменяющейся величины погрешность СИ зависит от скорости (частоты) изменения измеряемой величины таким образом, что выделить независимую от скорости (частоты) составляющую погрешности СИ, обусловленную только неидеальностью элементов СИ и воздействием на их параметры влияющих величин, не представляется возможным. Выделение динамической погрешности СИ, как суммируемой составляющей, допустимо только в частном, правда, весьма распространенном случае, когда можно считать, что СИ - линейное динамическое звено. Можно показать, что при данном условии, а также учитывая, что погрешности обычно достаточно малы, погрешность СИ допустимо приближенно представлять как сумму двух независимых составляющих - статической и динамической. При измерении постоянной или весьма медленно меняющейся величины погрешности СИ равна только одной из составляющих - статической, динамическая погрешность при этом равна нулю. Такое представление погрешности СИ не необходимо, но весьма удобно. Если погрешность СИ является суммой двух независимых составляющих, то удобнее нормировать эти составляющие раздельно. При этом упрощаются методы контроля характеристик погрешностей на соответствие нормам. Например, если СИ представляет собой линейное динамическое звено и для него отдельно нормированы динамические характеристики, то при поверке конкретных экземпляров СИ эти характеристики часто можно не контролировать. Если же нормируются характеристики полной погрешности СИ без выделения динамической и статической составляющих, то их придется контролировать при поверке, что весьма усложнит методику поверки, повысит ее трудоемкость. Поэтому тогда, когда это допустимо, целесообразно представлять погрешность СИ как сумму статической и динамической составляющих. Для СИ, представляющих собой линейные динамические звенья, такое приближенное представление допустимо. Рассмотрим это на примере измерительного преобразователя. Погрешность измерительного преобразователя по выходу - это, по определению, разность между истинной и номинальной функциями преобразования. Истинная функция преобразования измерительного преобразователя, на вход которого воздействует изменяющийся сигнал х(t), определяется его амплитудно-фазовой характеристикой G(jw) и некоторой аддитивной составляющей Da, не зависящей от входного сигнала, и в частотной области выражается формулой*
Тогда приведенная к выходу погрешность преобразователя при воздействии на его вход изменяющегося сигнала выражается формулой где Ksf - номинальный коэффициент преобразования. Амплитудно-фазовая характеристика линейного динамического звена, как известно, может быть представлена в виде
Можно представить где asf - номинальное значение коэффициента a0; Da0 - погрешность этого коэффициента, обусловленная собственными статическими свойствами преобразователя, не связанными с его динамическими свойствами. *Общий список обозначений приведен в приложении 1. Предположение о малости погрешности преобразователя сводится, в частности, к предположению о близости a0 к Кsf. Тогда можно принять Кsf = asf. Теперь (1.2) можно переписать в виде
Следствием предположения о малости погрешности преобразователя является также справедливость неравенства
Окончательно можно написать Первый член (1.7) представляет собой произведение не зависящей от w величины на х. С какой бы скоростью (или частотой) не изменялся x(t), это произведение от скорости (или частоты) изменения сигнала x(t) не зависит, а прямо пропорционально значению x(t). Фактически в этом произведении w не является аргументом. Для того, чтобы подчеркнуть это обстоятельство, этот аргумент при х не обозначен. При таком написании (1.7) свойства погрешности показаны более ясно. Если аргумент w при х написать, суть дела не изменится, но внешне формула будет выглядеть так, будто ее первый член зависит от w, чего в действительности нет. Первое слагаемое в (1.7) - это мультипликативная погрешность преобразователя, обусловленная неидеальностью собственных статических свойств преобразователя и воздействием влияющих величин, не связанная с динамическими свойствами преобразователя. Первые два слагаемых (1.7) определяют погрешность преобразователя, не зависящую от его динамических свойств. Их сумму можно назвать статической погрешностью преобразователя - Dsf. Коэффициенты третьего слагаемого можно, аналогично (1.4), представить как
Учитывая, что (1.7) есть приближенное выражение погрешности, и пренебрегая величинами второго порядка малости, (1.7) можно записать в виде
Выражение (1.9) представляет собой сумму трех слагаемых. Два первых - это статическая погрешность преобразователя, а третье зависит только от номинальных параметров преобразователя и от значения и частоты изменения измеряемого сигнала, т.е. определяется динамическими свойствами преобразователя и может быть названо динамической погрешностью Ddyn преобразователя
Таким образом, для СИ, представляющих собой линейные динамические звенья, при условии, что погрешность СИ является малой величиной по сравнению с выходным сигналом СИ, погрешность СИ может быть представлена суммой двух независимых составляющих: статической и динамической погрешностями СИ. Такое представление недопустимо для СИ, являющихся нелинейными динамическими звеньями. При оценке четырех составляющих инструментальной составляющей погрешности измерений, перечисленных выше, необходимо учитывать важную принципиальную особенность НМХ СИ. Нормы, регламентированные в НТД на СИ, отражают свойства не одного отдельно взятого экземпляра СИ, а свойства всей совокупности СИ данного типа. MX любого отдельно взятого экземпляра СИ данного типа могут быть любыми в пределах области значений, определяемой нормами. Это значит, что MX СИ данного типа должна быть рассмотрена как случайная величина; стохастические свойства генеральной совокупности этой случайной величины определяются нормами, регламентированными в НТД на СИ данного типа. Следовательно, указанные выше четыре составляющие инструментальной составляющей погрешности измерений являются случайными величинами. Дополнительная и динамическая погрешности случайны еще и потому, что влияющие величины и входной сигнал часто представляют собой случайные процессы. Таким образом, инструментальная составляющая погрешности измерений определяется как сумма случайных величин, т. е. как статистическая сумма (объединение) составляющих. Необходимо обратить внимание на то, что здесь не были учтены стохастические свойства отдельного экземпляра СИ, т. е. предполагалось, что метрологические свойства каждого отдельного экземпляра СИ вполне детерминированы и постоянны. Следовательно, даже если СИ не обладают случайными погрешностями, и все MX отдельных экземпляров СИ постоянны, инструментальная составляющая погрешности измерений, оцениваемая по НМХ СИ, должна рассматриваться как случайная величина. Учет случайных погрешностей СИ усложняет расчет погрешности измерений, но общий подход к расчету, т. е. необходимость статистического объединения, остается. Из изложенного вытекает основное необходимое свойство НМХ СИ: они должны быть такими, чтобы, пользуясь ими, можно было оценивать соответствующие составляющие инструментальной составляющей погрешности измерений как случайные величины (процессы) в форме, пригодной для статистического объединения. Рассматривая традиционно регламентируемые в НТД (до введения ГОСТ 8.009-84) MX СИ и формы их выражения, нетрудно установить, что они не удовлетворяют этому основному требованию. Нормирование MX СИ, как правило, было построено по следующей схеме. По отдельности нормировались пределы допускаемых значений: 1) основной статической погрешности; 4) времени изменения выходного сигнала, вызванного скачкообразным изменением входного сигнала от некоторого одного до некоторого другого уровня, как характеристики динамических свойств СИ. Кроме того, для СИ, входным сигналом которых является колебательный процесс с различными частотами, в той или иной форме нормировали частотные характеристики. При нормировании пределов допускаемых значений характеристик по пп. 1; 2; 3 научно обоснованное суммирование соответствующих составляющих может быть только арифметическим. В отношении получаемой при этом оценки погрешности измерений можно считать, что она будет «наибольшей возможной». Но эта «оценка сверху» практически всегда будет весьма далекой от действительности, так как практически невероятно, что при реальном применении СИ все суммируемые составляющие имеют свои наиболее допускаемые значения с одинаковым знаком. Поэтому подобный способ оценки погрешности измерений практически не используют. Иногда применяется квадратичное суммирование составляющих, однако оно в общем случае неправильно и может использоваться только в некоторых частных обоснованных случаях. Попытки использовать традиционно нормируемые MX СИ для оценки погрешности измерений, осуществляемых в современных реальных условиях, приводят к совершенно неправдоподобным, заведомо неверным результатам. Как следует из изложенного, это неизбежно вытекает из того обстоятельства, что, как правило, традиционные MX типов СИ не отражают статистических свойств совокупности экземпляров СИ, для которых их нормируют. Кроме того, в традиционных методах нормирования MX СИ не учитывают стохастический характер как влияющих величин. так и измеряемых величин (при измерениях меняющихся величин). Таким образом, традиционно применяемые способы нормирования MX СИ не позволяют ни достаточно достоверно оценивать инструментальную составляющую погрешности измерений, ни устанавливать соответствие СИ заданным допускаемым погрешностям измерений. Кроме того, для СИ различных видов обычно нормировали разные MX, в общем случае между собой не связанные, так что комплекс нормируемых характеристик не позволял обоснованно сравнивать между собой СИ различных видов, в частности, различные компоненты определенной ИС. Характеристики, предназначенные для отражения возможных случайных погрешностей СИ, во-первых, нормировали так, что оценить случайные погрешности измерений не представляется возможным, и, во-вторых, для разных СИ нормировали разные характеристики. Например, для электроизмерительных приборов нормировали вариацию показаний, а для приборов измерения давления и некоторых преобразователей - вариацию выходного сигнала и его непостоянство, причем хотя последние две характеристики нередко отражают одни и те же физические закономерности, тем не менее значения этих характеристик нормировались в отрыве друг от друга и сопоставить их было невозможно. Нормирование времени изменения выходного сигнала, как динамической характеристики, не позволяет оценить действительные погрешности измерений меняющихся величин. Возможно, что с таким положением в какой-то степени можно мириться в отношении лабораторных СИ, используемых для статических измерений в условиях весьма малых внешних воздействий и не являющихся компонентами ИС. Что же касается всех технических СИ, включая ИС, необходима была перестройка применяемых способов нормирования MX СИ, разработка единой системы нормирования MX СИ, удовлетворяющей необходимым требованиям. Этого требуют современные задачи развития народного хозяйства, неразрывно связанные с повышением эффективности измерений во всех областях, эффективности использования измерительной техники, чего невозможно добиться, не оценивая достаточно правильно погрешности технических измерений и выбирая СИ без удовлетворительных обоснований. 2. ГРУППЫ MX СИ.В соответствии с указанным выше в основу ГОСТ 8.009-84 положена следующая исходная предпосылка: НМХ СИ должны быть такими, чтобы в необходимых случаях было возможным статистическое объединение всех составляющих погрешностей СИ, отражаемых этими характеристиками, имеющихся в реальных условиях эксплуатации СИ. Эта предпосылка делает ГОСТ 8.009-84 строго и полностью применимым лишь для таких СИ, которые можно рассматривать как линейные. Для существенно нелинейных СИ ГОСТ 8.009-84 может быть и не пригоден. Для таких СИ надо применять специфические методы нормирования MX СИ, но также удовлетворяющие основному требованию - обеспечению возможности оценки инструментальной составляющей погрешности измерений в реальных условиях применения СИ по НМХ СИ. При разработке стандарта дополнительно учитывалось также важное требование о том, что НМХ должны отражать определенные физические свойства СИ и быть практически контролируемыми. С учетом этих основных требований в ГОСТ 8.009-84 регламентированы следующие новые группы MX СИ: 1) характеристики систематической и случайной составляющих погрешности СИ как случайных величин; спектральная плотность (нормализованная автокорреляционная функция) случайной составляющей погрешности и (для целей контроля) регламентированы наибольшие допускаемые значения систематической составляющей; 2) функции влияния влияющих величин на НМХ СИ и (в случае необходимости) функции совместного влияния нескольких влияющих величин; 3) динамические характеристики СИ - вид оператора и его коэффициенты; 4) характеристики СИ, отражающие их потенциальную способность к взаимодействию с любым из подключенных к их входу или выходу компонентов, таких как объект измерения, СИ и т. п., когда такое взаимодействие влияет на инструментальную составляющую погрешности измерений, например входные и выходные импедансы линейных измерительных преобразователей; 5) неинформативные параметры выходного сигнала СИ. Необходимо учитывать то важнейшее обстоятельство, что математически строгое решение сформулированной выше основной задачи нормирования MX СИ практически вряд ли возможно, по крайней мере, в настоящее время. Назначение ГОСТ 8.009-84 - создать предпосылки для получения более близких к действительности оценок инструментальной составляющей погрешности измерений, чем это можно делать по MX СИ, традиционно нормируемым. Задача обеспечения возможности определения по НМХ СИ идеально строгих оценок инструментальной составляющей погрешности измерений в настоящее время практически вряд ли может быть решена. Поэтому решалась задача нахождения компромисса между обеспечением возможности определения по НМХ СИ инструментальной составляющей погрешности измерений с практически достаточной достоверностью и требованием практической реализуемости необходимых методов установления и контроля НМХ СИ, а также методов оценки необходимых характеристик условий эксплуатации СИ и характеристик измеряемых процессов. Реализация указанного компромисса проявляется в учете всех влияющих технических и экономических факторов. Поэтому конкретные характеристики и нормы, а также методы испытаний для всех СИ не могли быть регламентированы в данном общем стандарте. В нем лишь даны общие требования к НМХ и методам испытаний СИ. Эта общая регламентация позволяет при разработке НТД на конкретные виды и типы СИ найти компромисс между указанными выше требованиями, обеспечивающий высокую эффективность СИ. Принципиальная особенность регламентированных в ГОСТ 8.009-84 новых пяти групп MX СИ заключается в том, что они позволяют определять не математически идеально строгие, а приближенные, но достаточно достоверные оценки инструментальной составляющей погрешности измерений в реальных условиях эксплуатации СИ. Конкретные причины такого подхода к регламентации номенклатуры НМХ СИ различны для разных групп характеристик, однако, как правило, они вытекают из двух основных обстоятельств. Подход к оценке характеристик СИ, учитывающий, что все свойства СИ данного типа являются стохастическими, основан на представлении о типе СИ, как о некоторой генеральной совокупности объектов, обладающих случайными свойствами. Все нормируемые характеристики СИ данного типа должны, следовательно, отражать свойства данной генеральной совокупности. Математически строгий подход к установлению и оценке всех нормируемых характеристик привел бы к чрезвычайно сложным экспериментальным и расчетным работам, как при разработке технической документации на СИ, так и при контроле СИ на соответствие нормам при выпуске из производства и находящихся в эксплуатации (при испытаниях и при поверке). Однако строгий математически подход в данном случае не оправдан практической необходимостью. Во-первых, рассматриваемые характеристики предназначены для оценки инструментальных составляющих погрешностей измерений, т. е. величин, малых по сравнению с результатами измерений. Погрешности оценок характеристик являются величинами второго порядка малости. Во-вторых, различные характеристики СИ могут иметь разную степень рассеяния и, следовательно, учет этого рассеяния может давать как ощутимые, так и малоощутимые результаты. В-третьих, строгость математических расчетов в рассматриваемых практических задачах нередко лишь кажущаяся. Известно, что математический аппарат, используемый при подобных строгих расчетах, справедлив при довольно узких ограничительных условиях, буквальное соблюдение которых на практике редко имеет место. Кроме того, достаточно строго проверить соблюдение этих условий чрезвычайно трудно. Второе обстоятельство, препятствующее реализации математически строгого подхода к установлению ряда характеристик СИ, заключается в следующем. ГОСТ 8.009-84 не распространяется на СИ, свойства которых не позволяют оценивать погрешность измерений по характеристикам, устанавливаемым этим стандартом; Здесь в основном имеются в виду СИ, являющиеся существенно нелинейными звеньями. Однако, практически подавляющее большинство реальных систем, в том числе СИ, которые по назначению должны быть линейными, в действительности лишь приближенно могут считаться линейными. Отличие их реальных свойств от свойств идеальных линейных звеньев приводит к тому, что строгие методы расчета инструментальных составляющих погрешностей измерений, в частности, динамических погрешностей, или учета входных свойств СИ, все равно приводят к не вполне точным результатам. На основании изложенного номенклатура характеристик, установленных стандартом, основана на приближенных представлениях о свойствах СИ данного типа. Методы нормирования MX СИ, предлагаемые в ГОСТ 8.009-84, можно рассматривать как существенное продвижение вперед по сравнению с методами, принятыми прежде. Предлагаемые новые методы нормирования направлены на удовлетворение насущных практических нужд измерительной техники. Однако нельзя считать, что эти методы являются окончательным и полным решением проблемы нормирования MX СИ. 2.1. Характеристики погрешности СИ.Первая группа характеристик отражает погрешности СИ, обусловленные собственными свойствами СИ. Если эти характеристики для СИ данного типа существенно изменяются при воздействии на СИ влияющих величин, то их нормируют для нормальных условий, т. е., как характеристики основной погрешности. Если же эти характеристики для СИ данного типа при указанных условиях изменяются незначительно по сравнению с нормированными значениями, то их нормируют для рабочих условий применения СИ. В этом случае основная погрешность и, следовательно, ее характеристики не выделяются. Поскольку первая ситуация является более характерной для современных СИ, при дальнейшем изложении будем полагать, что в первую группу входят характеристики основной погрешности. Моменты систематической составляющей D0s основной погрешности D0 - математическое ожидание М[D0s] и дисперсия D[D0s] или среднее квадратическое отклонение s[D0s] - характеристики, позволяющие при расчете характеристик инструментальной составляющей погрешности измерений по НМХ СИ приближенно учитывать разброс значений систематической погрешности для различных экземпляров СИ данного типа. Конечно, при строгом учете этого случайного разброса надо было бы использовать закон распределения вероятностей величины D0s. Однако это привело бы к неоправданному чрезвычайному усложнению методов расчета погрешностей измерений и контроля СИ на соответствие нормам. Характеристики М[D0s] и s[D0s] отражают свойства не каждого отдельного экземпляра СИ, а всей совокупности СИ данного типа, для которого они нормированы. Следовательно, они не могут служить критериями качества отдельных экземпляров СИ. При установлении нормируемых характеристик, отражающих основную погрешность каждого отдельного экземпляра СИ данного типа, необходимо выбрать ее математическую модель. Параметры этой модели и должны представлять собой НМХ, отражающие, с одной стороны, свойства, а с другой - требования к основной погрешности СИ. В основу
выбора математической модели основной погрешности СИ положено предположение о
том, что основные погрешности отдельных экземпляров СИ относятся к таким
нестационарным случайным процессам D0(t) которые в общем случае могут быть представлены суммой
математического ожидания М[D0] (или
систематической погрешности D0s), случайного стационарного центрированного
эргодического процесса D0(t) и случайной центрированной величины *Для аналого-цифровых
преобразователей и цифровых измерительных приборов в состав погрешности Такое представление является приближенным, однако если ввести некоторую условность в определение систематической погрешности D0s (см. ниже), оно будет достаточно хорошо отражать общие физические свойства СИ. С другой стороны, такое представление основной погрешности СИ позволяет установить относительно простые характеристики свойств СИ. Усложнение математической модели основной погрешности, существенно не улучшая оценки инструментальных составляющих погрешностей измерений, привело бы к весьма значительному усложнению как системы нормирования MX СИ, так и методов их контроля. Условность определения систематической погрешности D0s заключается в следующем. Обычно под систематической понимают погрешность, являющуюся постоянной, либо изменяющейся по известному закону, детерминированной величиной. Ее оценивают как среднее определенного количества реализации погрешности. При этом, если систематическая погрешность - функция времени, то реализации погрешности, усреднением которых определяют значение систематической погрешности в некоторый момент времени t, должны учитываться в течение такого небольшого интервала времени Dt, чтобы изменением систематической погрешности за этот интервал времени можно было пренебречь. В приведенном выше определении математической модели основной погрешности СИ как нестационарной случайной функции вся «нестационарность» отнесена к
составляющей D0s(t), поскольку
составляющая Однако, сфера практического использования понятия «систематическая погрешность» в общепринятом смысле, т. е. как детерминированной величины, крайне ограничена. Действительно, если эта погрешность определена как детерминированная величина и ее значение известно, то ее просто исключают введением поправки. Другого способа использования систематической погрешности как детерминированной величины быть не может. Если из физических соображений ясно, что некоторая составляющая погрешности постоянна или закономерно изменяется, т. е. по определению является систематической, но ее значение неизвестно, а известны лишь некоторые пределы, в которых это значение может находиться (так чаще всего и бывает), то учитывать эту погрешность можно только как случайную величину, лежащую в определенных пределах. В ГОСТ 8.009-84 характеристики систематической погрешности регламентированы, исходя из несколько усложненной трактовки ее свойств. Ее характеристики регламентированы как характеристики случайной величины, лежащей в определенных пределах: М[D0s]; s[D0s]; D0sp - пределы допускаемых значений. Первые две характеристики используются при расчетах характеристик инструментальных составляющих погрешностей измерений, характеристику D0sp контролируют при поверках. В этих характеристиках в общем случае не отражена нестационарность погрешности СИ, которая, как указано выше, в принятой модели отнесена к систематической погрешности. В случае целесообразности, характеристики М[D0s] и s[D0s] могут выражаться как функции времени. Однако вряд ли такое представление окажется целесообразным во многих случаях. Следовательно, в отношении практического учета нестационарности погрешности СИ почти полностью сохраняется положение, сложившееся в действующих НТД на СИ. Это связано с тем, что, как правило, отражение нестационарности погрешности СИ в НМХ привело бы к практически нереализуемым методам испытаний СИ. Эта нестационарность имеет, как известно, такой характер, что соответствующие изменения погрешности происходят весьма медленно - в течение месяцев. Контролировать их практически невозможно. Кроме того, использовать соответствующие MX СИ при расчете характеристик инструментальной составляющей погрешности измерений на практике вряд ли возможно. Рассматриваемое свойство погрешностей СИ в необходимых случаях предполагается учитывать лишь заданием характеристик М[D0s] и s[D0s] как функций времени. Надо отметить, что нестационарность погрешности СИ следует практически учитывать при назначении межповерочного интервала. Он должен устанавливаться исходя из того, чтобы вероятность выхода MX (в основном, характеристик погрешности) СИ за пределы допускаемых значений в течение межповерочного интервала не превышала заданного значения. Физический смысл составляющих в формуле (2.1) следующий. Составляющая D0s(t) включает в себя постоянные и настолько медленно, в том числе случайно, изменяющиеся во времени погрешности, что их изменением можно пренебречь за максимально возможное время проведения опытов, при которых применяют СИ данного типа. Таким образом, предполагается, что в течение обычной для СИ данного типа продолжительности опытов составляющая D0s(t) погрешности СИ является постоянной (для СИ, для которых это предположение несправедливо, характеристики систематической погрешности М[D0s] и s[D0s] могут регламентироваться как функции времени). Кроме того, при контроле погрешности СИ данную составляющую оценивают путем усреднения ряда реализаций погрешности, полученных за некоторый малый интервал времени. Вследствие этих двух обстоятельств составляющая D0s(t) и отнесена к систематическим. Составляющая D0s(t) основной погрешности СИ обусловлена неточностью градуировки и регулировки СИ, а также медленными временными изменениями (типа временного старения) свойств материалов и элементов; из которых состоит СИ. Составляющая
и Удобство такого разделения погрешности D0(t) обусловлено следующими соображениями. По способам использования выходных сигналов СИ все измерения могут быть разделены на две группы. Первая группа, которую условно можно назвать группой простых измерений, характеризуется тем, что каждое значение выходного сигнала (результат измерения) используют по отдельности, различные результаты измерений не подвергают никакой совместной обработке. Вторая группа, условно называемая группой сложных измерений, характеризуется тем, что отдельные результаты измерений подвергают какой-либо совместной обработке с целью получения конечного результата, являющегося функцией отдельных первичных результатов измерений [1]. Во вторую группу входят, например, косвенные измерения. За окончательную оценку погрешности измерений обычно принимают интервал, за границы которого с заданной вероятностью погрешность не выходит. Для оценки этого интервала при измерениях первой группы можно пользоваться первыми двумя моментами распределения погрешности измерений - математическим ожиданием (систематической погрешностью) и дисперсией. Для оценки интервала погрешности при измерениях второй группы знания первых двух моментов распределения недостаточно. Необходимо вводить в расчет также параметр двумерного распределения погрешности - автокорреляционную функцию погрешности [2]*. * Если конечный результат измерений получается обработкой данных, полученных с помощью различных СИ, необходимо пользоваться не автокорреляционной, а взаимно-корреляционной функцией погрешности. Здесь этот вопрос не рассматривается, так как нормировать взаимно-корреляционную функцию погрешностей даже только двух СИ невозможно. Однако при оценке погрешности ИС даже при измерениях первой группы также необходимо знать автокорреляционные функции (или однозначно с ней связанные спектральные плотности) основных погрешностей СИ, входящие в ИС. Таким образом, при оценке характеристик инструментальных составляющих погрешностей измерений в общем случае необходимо знать автокорреляционную функцию основной погрешности СИ. Из
определений составляющих погрешности D0(t)
по формуле (2.2) ясно, что подход к определению автокорреляционных
функций разных составляющих должен быть различным. Очевидно, что реализации
составляющих Далее очевидно, что в пределах возможных длительностей опытов коэффициент корреляции между реализациями составляющей D0s(t) при отдельных измерениях практически не отличается от единицы (систематическая погрешность). Для нее, следовательно, определять автокорреляционную функцию нет необходимости. Для составляющей В большинстве случаев
составляющую Математическая модель (2.3) основной погрешности СИ включает:
Dоs - систематическую погрешность, представляющую собой настолько медленно изменяющийся случайный процесс, что в течение обычной продолжительности опытов она может быть принята постоянной; ее характеристика - предел допускаемых значений D0sр *. * Необходимо обратить внимание на следующее обстоятельство. В любом случае, когда нормируют «предел допускаемых значений» какой-либо величины (основной систематической погрешности СИ, погрешности СИ, вариации выходного сигнала (показания) СИ и др.), под этим «пределом» следует понимать интервал, если значение величины может иметь только один знак (плюс или минус) или половину интервала, если значение величины с одинаковой вероятностью может иметь знаки (плюс или минус), в котором с вероятностью, равной единице, находится действительное значение величины. Кроме изложенных особенностей принятой математической модели основной погрешности СИ, в стандарте учтены еще два принципиальных предположения о свойствах основной погрешности всей совокупности СИ, объединяемых понятием «тип СИ», т. е. совокупности СИ, имеющих одинаковое назначение, одинаковые схему и конструкцию и удовлетворяющих одним и тем же техническим требованиям, регламентированным в технических условиях на СИ данного типа. 1. Основные погрешности отдельных экземпляров СИ одного и того же типа между собой несколько различаются. Указанные выше характеристики всех трех составляющих модели (см. формулу 2.3) должны рассматриваться, в свою очередь, как случайные величины, для каждого экземпляра СИ данного типа проявляющиеся своими отдельными реализациями, а для всего типа СИ представляющие генеральные совокупности. Следовательно, для каждой из характеристик составляющих модели следовало бы нормировать свои статистические характеристики, например, математическое ожидание и среднее квадратическое отклонение систематической составляющей погрешности Dos; математическое ожидание и среднее квадратическое отклонение среднего квадратического отклонения некоррелированной составляющей погрешности Douc и т. д. Однако из физических соображений можно предположить, что разброс характеристик случайных составляющих погрешности СИ для различных экземпляров СИ одного и того же типа меньше самих этих характеристик. Поэтому характеристики разброса (между отдельными экземплярами СИ данного типа) характеристик случайных составляющих погрешности СИ приняты за величины второго порядка малости. Например, среднее квадратическое отклонение средних квадратических отклонений случайной погрешности для СИ данного типа принимается пренебрежимо малым и не регламентируется. Разброс же систематической погрешности для различных экземпляров СИ одного и того же типа существенен по сравнению с самой систематической погрешностью для каждого экземпляра СИ. Исходя из стремления к максимально возможному упрощению системы нормирования MX СИ, для среднего квадратического отклонения случайной составляющей погрешности в ГОСТ 8.009-84 регламентирован только предел допускаемых значений, а для систематической погрешности также ее математическое ожидание и среднее квадратическое отклонение по совокупности СИ данного типа. Такое упрощение системы нормирования приводит к некоторому завышению расчетных значений инструментальных составляющих погрешностей измерений, подсчитываемых по нормированным характеристикам СИ, поскольку при расчете будут учитываться максимально возможные (допускаемые), а не средние для данного типа СИ характеристики случайной погрешности. Несмотря на это принят именно такой подход к нормированию, так как в противном случае как система нормирования, так и способы контроля (испытаний и поверки) СИ весьма существенно усложнились бы. 2. При обосновании модели по
формуле (2.3)
основной погрешности СИ не учитывались наблюдаемые в различных СИ явления типа
трения, люфта, гистерезиса и т. п. Как показано в [3], эти явления можно учесть, если
приближенно принять, что случайная погрешность СИ, вызываемая этими явлениями,
представляет собой случайную величину Для СИ, обладающих трением, люфтом, гистерезисом и т. п., математическая модель основной погрешности должна быть записана в виде где Таким образом, правая часть
формулы (2.4) содержит систематическую
составляющую основной погрешности СИ (D0s), две случайные
составляющие основной погрешности СИ ( В качестве характеристики
случайной погрешности Таким образом, окончательная
модель основной погрешности СИ, для которой регламентируются характеристики,
имеет вид (2.4). Отдельно
регламентированы характеристики составляющих D0s - (М[D0s], s[Dоsр], D0s) и Что касается составляющих Нормируемые характеристики
следует экспериментально определять или контролировать. Это значит, что по
отдельности необходимо определять характеристики систематической составляющей Dоs, суммы
составляющих ( При наличии гистерезиса
эксперимент осуществляется сначала при подходе к контролируемой точке х
диапазона измерений со стороны меньших, а затем - со стороны больших значений
(или наоборот). При этом получаются два множества реализации погрешности,
группирующихся вокруг двух разных центров, обусловленных наличием гистерезиса
(вариации). Это вызывает определенное затруднение в определении характеристик
составляющих погрешности. Для преодоления этого затруднения вводят
предположение о том, что при подходе с одной стороны разброс реализации
погрешности вокруг соответствующего центра группирования подчиняется тому же
закону распределения вероятностей, что и разброс вокруг другого центра (при
подходе с другой стороны). Это предположение может считаться обоснованным
потому, что оба центра группирования практически расположены настолько близко,
что систематическая составляющая Dоs и закон распределения случайной составляющей ( Последовательность этапов при вычислениях следующая: 1)
имеются реализации погрешности 2)
определяются центры группирования 3)
определяются центрированные реализации в каждой группе 4)
определяется оценка 5)
определяется оценка 6)
определяется оценка Этим формулам соответствуют формулы приложения 2 к ГОСТ 8.009-84. В изложенных рассуждениях пренебрегали некоторым отличием центров группирования реализации погрешности (при подходе снизу и сверху) от соответствующих математических ожиданий, которые остаются неизвестными. Это пренебрежение можно считать допустимым, поскольку при достаточно большом п указанные отличия будут незначительными и к практически заметным последствиям приводить не будут. Вместе с тем, при указанном пренебрежении, общий подход и обоснования практической правильности расчетных формул получаются достаточно простыми и ясными. ГОСТ 8.009-84 допускает при
малой случайной составляющей 2.2. Характеристики дополнительной погрешности СИ (чувствительности к влияющим величинам).Дополнительная погрешность СИ обусловлена изменениями влияющих величин относительно своих нормальных значений. Она проявляется постольку, поскольку параметры материалов и элементов, из которых состоит СИ, и конструктивные параметры СИ зависят от значений влияющих величин. Следовательно, дополнительная погрешность является функцией влияющих величин. Для каждого экземпляра СИ эта функция имеет определенный вид и определенные значения параметров. Наиболее представительной характеристикой дополнительной погрешности является функция зависимости характеристик погрешности от влияющих величин, имеющая определенные параметры, т. е. функция влияния. Для разных экземпляров СИ данного типа могут различаться как вид рассматриваемой функции, так и ее параметры. Однако в принципе, для всех экземпляров СИ данного типа эти функции должны быть подобны, а их параметры близки. Поэтому в качестве основной характеристики дополнительной погрешности принята некоторая средняя для СИ данного типа функция зависимости погрешности СИ от изменения влияющих величин с указанием ее параметров. Такая функция названа номинальной функцией влияния. Кроме того, должны также нормироваться пределы допускаемых отклонений функций влияния относительно номинальной функции, в которых должны находиться функции влияния всех экземпляров СИ данного типа. Для некоторых типов СИ характерно то обстоятельство, что функции влияния для различных экземпляров СИ данного типа существенно между собой различаются. Это иногда наблюдается для таких СИ, в схемах которых применена компенсация влияния влияющих величин, например, температуры. Для типов СИ, характеризующихся существенными различиями видов и параметров функций влияния для разных экземпляров СИ, нормирование номинальных функций влияния, по-видимому, не имеет смысла. В этих случаях целесообразно нормировать или граничные функции влияния (и тогда для каждого экземпляра СИ потребитель должен определять индивидуальную функцию влияния, которой затем он сможет пользоваться для оценки инструментальной составляющей погрешности измерений в реальных условиях применения СИ) или другую характеристику дополнительной погрешности, относящуюся к группе традиционных характеристик, - пределы допускаемых значений дополнительной погрешности, т. е. изменений погрешности. Влияющие величины могут вызывать изменения не только погрешности СИ, но и других MX СИ. Поэтому для необходимых случаев целесообразно предусмотреть нормирование функций влияния и на другие MX СИ. Особенности нормирования функций влияния не зависят, в общем случае, от того, на какую характеристику функции влияния нормируются. Функции влияния Y(x) определены как зависимости изменений MX СИ от изменений влияющих величин в рабочих условиях применения СИ. Их следует нормировать для тех MX, которые нормируются для нормальных условий. Если некоторые MX нормируют для рабочих условий применения СИ, то соответствующие функции Y(x) не нормируют. Пусть, например, характеристики погрешности СИ нормируют следующим образом. Для нормальных условий: М[Dos], s[Dos], Dosp - характеристики
систематической составляющей основной погрешности Для рабочих условий: Следовательно, функции влияния должны быть нормированы для систематической погрешности и среднего квадратического отклонения случайной погрешности, а для автокорреляционной функции и вариации функции влияния не нормируют. То же относится к любым другим НМХ СИ. Необходимо, однако, заметить что, далеко не все MX должны нормироваться для нормальных условий. Поскольку почти все MX влияют лишь на погрешность измерений, можно считать, что изменения большинства из них под воздействием влияющих величин вызывают изменения погрешности измерений второго порядка малости. Тогда соответствующие MX следует нормировать для рабочих условий применения СИ, а функции влияния на них не нормировать. В этом отношении, по-видимому, будет в большинстве случаев справедлива существующая практика, когда нормируют изменения под воздействием влияющих величин только погрешности СИ, а остальные MX нормируют для рабочих условий применения СИ. Важен вопрос о том, почему и в каких случаях от традиционного нормирования пределов допускаемых дополнительных погрешностей необходимо перейти к нормированию функции влияния. Учитывая сделанные выше замечания о том, для каких MX следует нормировать функции влияния, в дальнейшем будем рассматривать функции влияния на погрешность СИ. Однако все изложенное ниже в равной степени справедливо и для функции влияния на другие MX СИ. Характеристиками, традиционно определяющими влияние влияющих величин на погрешность СИ, являются наибольшие допускаемые изменения (пределы допускаемой дополнительной погрешности) ± Dср погрешности, имеющие место при изменении влияющей величины на некоторое установленное значение ± Dx относительно нормального значения. Если в реальных условиях эксплуатации влияющая величина может принимать разные значения в пределах от xн до xв, причем xн < xref < xв, где xref - нормальное значение влияющей величины, то при традиционном нормировании можно определить лишь наибольшие возможные изменения погрешности СИ.
При оценке инструментальной
составляющей погрешности измерений в реальных условиях применения СИ, вызванной
воздействием данной влияющей величины, имеется только одна возможность: учесть
наибольшее возможное
или
Погрешность D СИ в реальных условиях может быть определена лишь как арифметическая сумма предела допускаемой основной погрешности Dор и наибольших допускаемых изменений погрешности СИ, вызванных влияющими величинами x1, x2, ..., xl: По причинам, подробно рассмотренным в разд. 1, значение D, определенное по формуле (2.6), практически всегда будет весьма существенно превышать значения действительной погрешности. Таким образом, характеристика дополнительной погрешности СИ, традиционно регламентируемая, не позволяет оценивать действительную погрешность СИ в реальных условиях применения с приемлемой достоверностью. Функции влияния Y(x) определяют дополнительную погрешность как функциональную связь между погрешностью СИ и вызывающими ее изменениями влияющих величин. Обозначим Dx = x - xref, (2.7) где x - текущее значение влияющей величины в реальных условиях применения СИ. Тогда для погрешности СИ в реальных условиях справедливо выражение D = D0 + Dс, где Dс - дополнительная погрешность, вызванная влияющими величинами x. Функции влияния определяют зависимость статистических характеристик дополнительной погрешности Dс от величины Dx. Математическое ожидание (систематическая составляющая) и дисперсия дополнительной погрешности выражаются, соответственно,
где Очевидно, что характеристики погрешности выражаются (для простоты считаем, что вариация отсутствует) как В формулы (2.10) и (2.11) входят величины, нормируемые для СИ данного типа. Поэтому по ним определяют характеристики погрешности любого экземпляра СИ данного типа. Если для конкретного экземпляра СИ известно значение его основной систематической погрешности Dos, то
В такой удобной форме дисперсия
погрешности может быть записана в случае, если нормирована функция влияния
именно на дисперсию случайной погрешности. В ГОСТ 8.009-84 предусмотрено
нормирование в качестве характеристики случайной погрешности ее среднего
квадратического отклонения где Ys(x) - функция влияния на среднее квадратическое отклонение случайной составляющей погрешности. В приведенном виде формулы (2.10) -
(2.15) справедливы в тех случаях, когда величины Dx учитываются как известные
детерминированные отклонения влияющих величин от нормальных значений. Если же
величины Dx
учитываются как случайные величины или функции, обладающие своими
математическими ожиданиями и характеристиками разброса, то формулы (2.10) -
(2.15) должны быть изменены. При этом условии функции влияния перестают быть
детерминированными функциями, а становятся функциями случайных аргументов. Это
обстоятельство особенно существенно для функции влияния на систематическую
погрешность, т. е. для функции
а в формуле (2.11) - дополнительный член В отношении функции влияния на
дисперсию На основании изложенного
рекомендуется при случайном характере изменений величины x
рассматривать функции влияния на дисперсию Таким образом, при случайном характере величин x формула (2.17) принимает вид:
Аналогично видоизменятся формулы (2.14) и (2.15) Определим величины Функции влияния могут иметь различный вид. В простейшем случае они являются линейными
Тогда
где Если то
Аналогично находим и Для более сложных функций влияния необходимые их статистические характеристики могут быть определены по правилам нахождения подобных характеристик функций случайного аргумента. Таким образом, нормирование
функций влияния Наиболее просто задача решается для таких СИ, для которых функции влияния разных величин (например, температуры и напряжения питания) взаимно независимы. На практике могут встречаться СИ, для которых функции влияния разных величин взаимно зависимы. Тогда нормируют функцию совместного влияния нескольких величин Y(x1, x2, …, xl), которую и используют при расчетах характеристик инструментальной составляющей погрешности измерений. 2.3. Динамические характеристики.Динамические характеристики, регламентированные в ГОСТ 8.009-84, отражают динамические свойства СИ. Традиционно эти свойства представляют, как правило, двумя характеристиками: временем установления показаний (выходного сигнала) и амплитудно-частотной (редко фазово-частотной) характеристикой. Первая характеристика не может быть использована при расчете динамической составляющей погрешности измерений. Ею можно оценить лишь время, необходимое для проведения единичного измерения. Частотные характеристики, если их нормируют в том или ином виде, выражаются как наибольшие допускаемые изменения амплитуды или фазы синусоидального выходного сигнала СИ при изменении частоты входного синусоидального сигнала, с постоянными амплитудой и фазой. Эти характеристики могут позволить оценить наибольшую возможную динамическую составляющую погрешности измерений при граничных значениях частоты входного сигнала, но только лишь для тех случаев, когда входной сигнал - синусоидальный. Это весьма частный случай современной измерительной техники. Поэтому практически частотные характеристики в таком виде, как их традиционно нормируют, являются скорее качественными характеристиками и для расчета динамической составляющей погрешности измерений при входном сигнале, характеризуемом некоторым спектром частот, непригодны. Динамические свойства СИ влияют не только на динамическую составляющую погрешности измерений. В тех случаях, когда СИ комплектуют в ИС, динамические свойства СИ влияют и на статическую погрешность ИС. В любой ИС имеется последовательное соединение нескольких СИ. Последующие в этом соединении СИ преобразуют (трансформируют) статические погрешности предыдущих СИ. Как показано выше, статическая погрешность СИ в общем случае представляет собой случайный процесс, т. е. характеризуется некоторым частотным спектром. При нормировании погрешности это свойство отражается автокорреляционной функцией или спектральной плотностью. Следовательно, преобразование статической погрешности предыдущего в системе СИ последующим СИ будет зависеть и от динамических свойств последующего СИ. Для оценки статической погрешности ИС необходимо иметь возможность определить влияние динамических свойств некоторого СИ на преобразование им статической погрешности (случайного процесса) другого СИ, включенного в ИС перед ним. Частотные характеристики, традиционно нормируемые, такой возможности не дают, поэтому наряду с характеристиками динамических свойств СИ, традиционно нормируемыми, пригодными в указанных выше частных случаях, в ГОСТ 8.009-84 предусмотрены другие характеристики, более полно отражающие динамические свойства СИ. Надо отметить, что по этим «новым» динамическим характеристикам достаточно просто могут быть определены и указанные выше характеристики, нормируемые традиционно. В ГОСТ 8.009-84 предусмотрено нормирование таких динамических характеристик СИ, которые позволяют оценивать искажения СИ любых изменяющихся сигналов, поступающих на их вход - исследуемых при измерениях (динамическая составляющая погрешности измерений), и сигналов, эквивалентных статической погрешности СИ, предвключенных к данному СИ в ИС (статическая погрешность ИС). Для линейных СИ такими характеристиками являются передаточная функция (или амплитудно-фазовая характеристика), переходная, импульсная и т. п. характеристики. Все они относятся к группе так называемых полных динамических характеристик, представляющих собой функции, связывающие между собой изменяющийся во времени входной сигнал и вызываемый им выходной сигнал СИ. Эти характеристики для линейных звеньев между собой связаны однозначно, поэтому в каждом конкретном случае следует нормировать ту из них, которой в данном случае удобнее пользоваться и которую удобнее экспериментально оценивать (контролировать). Полные динамические характеристики линейных аналоговых СИ однозначно связаны между собой следующими соотношениями: переходная характеристика импульсная переходная характеристика
амплитудно-фазовая характеристика
где А(w) и j(w) - амплитудно- и фазово-частотная характеристики, соответственно; передаточная функция
Если СИ обладает амплитудно-фазовой характеристикой минимально-фазового типа, то его фазово-частотная характеристика однозначно связана с логарифмической амплитудно-частотной характеристикой
где и = ln(w*/w), w* - переменная интегрирования, имеющая размерность круговой частоты. Если динамические свойства СИ описываются дифференциальным уравнением
с нулевыми начальными условиями, то передаточная функция и амплитудно-фазовая характеристика имеют дробно-рациональное представление с коэффициентами из уравнения (2.32)
Для оценки инструментальной составляющей погрешности измерений наиболее удобна амплитудно-фазовая характеристика, однако, она не всегда может быть экспериментально определена с помощью прямых методов измерений. С точки зрения экспериментального определения наиболее удобными динамическими характеристиками являются переходная и амплитудно-частотная характеристики. В самом деле, при подаче на вход СИ испытательного ступенчатого сигнала единичного размера можно с помощью прямых измерений выходного сигнала получить отсчеты (или запись) переходной характеристики. Амплитудно-частотная характеристика также может быть получена с помощью прямых измерений амплитуды выходных гармонических сигналов при действии на входе гармонических сигналов требуемой частоты и единичной амплитуды. Однако здесь возникает трудность, связанная с ограниченными возможностями точного воспроизведения формы сигналов тех или иных измеряемых величин. Например, затруднительно воспроизвести гармоническое изменение температуры, концентрации компонентов сложных веществ, влажности, расхода и других измеряемых величин. С другой стороны, скачкообразное изменение таких величин, как, например, скорости, ускорения и других, воспроизвести труднее, чем гармоническое. Все перечисленные обстоятельства следует учитывать при выборе той или иной динамической характеристики для нормирования. Нормировать рекомендуется такую характеристику, которая может быть экспериментально определена с помощью наиболее простых методов измерений. Допустим, что в конкретном случае для датчика температуры выбрана в качестве нормируемой переходная характеристика, которая непосредственно не может быть использована для вычисления динамической составляющей погрешности измерений. В таком случае, наряду с нормируемой характеристикой, которая должна контролироваться при испытаниях СИ, целесообразно в качестве справочной указывать ту характеристику, которую использовать удобнее. Эта характеристика не должна контролироваться при испытаниях, потому что между динамическими характеристиками существует однозначная связь, поэтому, если нормируемая характеристика оказывается в норме, то и справочная характеристика также соответствует записанной в НТД. Для определения справочной характеристики обычно пользуются номинальной нормированной характеристикой и по ней находят требуемую характеристику. Для моделирования динамической составляющей погрешности измерений наиболее удобны импульсная переходная и амплитудно-фазовая характеристики, а также передаточная функция. Импульсная переходная характеристика используется при цифровом моделировании путем приближенного вычисления выходного сигнала СИ Амплитудно-фазовая характеристика и передаточная функция используются для моделирования СИ как на аналоговых, так и на цифровых вычислительных машинах. Для расчета MX измерительных каналов ИС, состоящих из последовательно соединенных СИ (усилителей, коммутаторов, аналого-цифровых преобразователей и т. п.), наиболее приемлемы передаточная функция и амплитудно-фазовая характеристика. Так, передаточная функция последовательно соединенных преобразователей равна произведению передаточных функций отдельных преобразователей. При параллельном соединении передаточная функция такого соединения равна сумме передаточных функций составляющих. Известны правила вычисления передаточных функций звеньев, охваченных обратной связью. Такими же свойствами обладает амплитудно-фазовая характеристика. Что касается импульсной переходной характеристики, то для последовательного соединения она равна свертке импульсных переходных характеристик отдельных блоков, а для параллельного соединения - сумме импульсных характеристик. Основной задачей является определение измеряемой величины по известному выходному сигналу и известной динамической характеристике. По сути дела, решение этой задачи приводит к частичной компенсации динамической составляющей погрешности. Если известна импульсная переходная характеристика, то задача сводится, к нахождению x(t) из интегрального уравнения (2.35). Следует отметить, что принятые в ГОСТ 8.009-84 динамические характеристики СИ до настоящего времени получили небольшое распространение лишь в НТД на СИ. В теории и практике автоматического регулирования и управления, автоматических устройств, в теории и практике связи, передачи информации, т. е. в областях, где измерительная техника и СИ являются важнейшей составной частью, подходы к оценке динамических погрешностей, на которых основан ГОСТ 8.009-84 и принятые в нем динамические характеристики СИ, применяют в течение многих лет и в мировой практике давно стали классическими. Примеры нормирования динамических характеристик следующие. Пример 1. Для СИ температуры и других СИ теплового действия (например, термоанемометров) характерным динамическим свойством, вызывающим динамическую составляющую погрешности измерения, является тепловая инерция. Поэтому, как правило, эти СИ являются динамическими звеньями первого порядка. Примеры графического представления номинальных динамических характеристик и наибольших допускаемых отклонений приведены на рис. 1. Номинальные динамические характеристики отмечены индексом sf. На рис. 2 приведены примеры нормирования динамических характеристик путем указания граничных динамических характеристик. Индексом R на рисунке отмечена реальная динамическая характеристика конкретного экземпляра СИ. Нормированные номинальные динамические характеристики в аналитическом виде (в виде функции) выражаются следующим образом: переходная характеристика импульсная переходная характеристика амплитудно-фазовая характеристика передаточная функция амплитудно-частотная характеристика фазово-частотная характеристика где Т - постоянная времени; Ksf - номинальный статический коэффициент преобразования (при w0 = 0). Частная динамическая характеристика tr указана на рис. 1, а и 2, а. Рис. 1. Номинальные динамические характеристики и наибольшие допускаемые отклонения от них для СИ, являющихся динамическими звеньями первого порядка: а - переходные; б - импульсные переходные; в - амплитудно-фазовые; г - амплитудно- и фазово-частотные. Пример 2. Пример графического представления номинальной переходной характеристики и наибольших допускаемых отклонений от нее для газоанализатора, основанного на эффекте переноса нагретых ионов кислорода в магнитном поле, представлен на рис. 3, где через td обозначено время транспортирования пробы газа (чистого запаздывания) из среды в чувствительный элемент газоанализатора. Рис. 2. Пример нормирования динамических характеристик путем указания граничных динамических характеристик для СИ, являющихся динамическими звеньями первого порядка. Обозначения те же, что на рис. 1. Пример 3. Если
выходной сигнал СИ теплового действия усиливается измерительным усилителем,
обладающим передаточной функцией Ga(S), то передаточная
функция образованного таким образом составного СИ равна произведению Амплитудно-фазовая характеристика определяется аналогично:
где Остальные характеристики выражаются следующим образом:
Здесь динамические характеристики с индексом а относятся к усилителю. Рис. 3. Переходная характеристика газоанализатора. Пример 4. Наиболее распространены СИ, динамические свойства которых описываются дифференциальными уравнениями второго порядка: пьезоэлектрические и потенциометрические акселерометры, сейсмические и маятниковые виброметры и др. Примеры графического представления номинальных динамических характеристик этих СИ и наибольших допускаемых отклонений приведены на рис. 4. При нормировании эти характеристики в аналитическом виде (в виде функций) выражаются следующим образом: переходная характеристика
импульсная переходная характеристика
амплитудно-фазовая характеристика
Рис. 4. Номинальные динамические
характеристики и наибольшие допускаемые отклонения от них для СИ, являющихся
динамическими звеньями второго порядка (пьезоэлектрические и потенциометрические
акселерометры, сейсмические и маятниковые виброметры и т. п.). Рис. 4. Продолжение. передаточная функция
амплитудно-частотная характеристика
фазово-частотная характеристика
где Ksf - номинальный коэффициент преобразования; Т - постоянная времени; g - коэффициент демпфирования. Обозначения на рис. 4 те же, что на рис. 1. Как видно из представленных характеристик, эти СИ не реагируют на постоянную во времени измеряемую величину: при w = 0, G(jw) = 0. К другой группе СИ, описываемых дифференциальными уравнениями второго порядка, относятся, например, осциллографические гальванометры, измерительные усилители, СИ силы, давления и др. Примеры графического представления номинальных динамических характеристик этих СИ и наибольших допускаемых отклонений приведены на рис. 5. При нормировании эти характеристики в аналитическом виде (в виде функций) выражаются следующим образом: переходная характеристика
импульсная переходная характеристика
амплитудно-фазовая характеристика
передаточная функция
амплитудно-частотная характеристика
фазово-частотная характеристика
где Ksf - номинальный коэффициент преобразования; Т - постоянная времени; g - коэффициент демпфирования. Обозначения на рис. 5 те же, что на рис. 1 и 4. На рис 6 приведены примеры графического представления граничных динамических характеристик средств измерений второго порядка. Обозначения те же, что и на рис. 2. Пример 5. Более высокий порядок динамических характеристик СИ может возникать, например, при последовательном соединении различных устройств. Например, наличие трубки, отводящей давление от места измерения к чувствительному элементу СИ давления эквивалентно включению перед этим СИ динамического звена первого порядка. Если постоянная времени этого звена больше постоянной времени СИ давления, то примером номинальной амплитудно-частотной характеристики такого соединения может быть:
Графически эта характеристика представлена на рис. 7. Такой же вид имеют, например, амплитудно-частотные характеристики осциллографических гальванометров с капельным успокоением растяжек. Размерности нормируемых динамических характеристик: переходной, амплитудно-фазовой характеристики, передаточной функции и амплитудно-частотной характеристики: размерность [y(t)] размерность [x(t)] импульсной переходной характеристики: размерность [y(t)] размерность [tx(t)] фазово-частотной характеристики - угловые единицы. Рис. 5. Номинальные динамические характеристики и наибольшие допускаемые отклонения от них для СИ, являющихся динамическими звеньями второго порядка (осциллографические гальванометры, измерительные усилители и т. п.). Обозначения те же, что на рис. 1.
Рис. 5. Продолжение.
Рис. 6. Примеры нормирования динамических характеристик путем указания граничных динамических характеристик для СИ, являющихся динамическими звеньями второго порядка: а - переходные; б - импульсные; в - амплитудно-частотные. Рис. 7. Номинальная амплитудно-частотная характеристика и наибольшие допускаемые отклонения от нее для СИ, являющихся динамическими звеньями третьего порядка. Возможности применения динамических характеристик для оценки динамической погрешности СИ кратко, проиллюстрируем на примере передаточной функции. Передаточная функция G(S) СИ может быть нормирована, например, в виде
Должны быть нормированы вид
функции (2.36), номинальные значения На вход СИ подается сигнал x(t). Выходной сигнал в операторной форме выражается. Y(S) = G(S) · X(S), (2.37) где X(S) - операторное выражение входного сигнала. Номинальная статическая функция преобразования СИ может быть принята в виде
Тогда динамическая погрешность СИ по выходу в операторной форме выражается формулой где Динамическая погрешность СИ по входу выражается формулой Выражения (2.40) и (2.42) позволяют по нормированной динамической характеристики Gsf(S) оценить динамическую составляющую погрешности измерений данным СИ величины x(t), частотные свойства которой должны быть ориентировочно известны. Пусть, например, измеряемая величина представляет собой стационарный центрированный случайный процесс, спектральная плотность которого Sx(w) приближенно известна*. Тогда математическое ожидание динамической погрешности СИ равно нулю, а ее дисперсия выражается формулой * В ГОСТ 8.009-84 и во всех связанных с ним НТД под
спектральной плотностью понимается функция Если измеряемая величина
представляет собой мгновенное значение гармонического сигнала
т. е. Ddyn.in представляет собой также гармонический сигнал с амплитудой
Математическое ожидание этой погрешности равно нулю, а дисперсия На практике встречаются также случаи, когда измеряемая величина может практически рассматриваться как гармонический сигнал фиксированной частоты, но со случайно изменяющимися амплитудой АM и фазой j:
При некоторых довольно общих условиях такой сигнал является стационарным и его автокорреляционная функция выражается как [4]:
где Спектральная плотность такого сигнала выражается как в [5]
где d(w - w1); d(w + w1) - дельта-функции Дирака, если
Математическое ожидание динамической составляющей погрешности измерений такого сигнала равно нулю, а дисперсия (2.43) выражается как:
или в соответствии с правилами интегрирования дельта-функций Выражение (2.41) может быть представлено в виде амплитудно-фазовой характеристики
где Asf(w) - амплитудно-частотная и jsf(w) - фазово-частотная характеристики СИ, нормируемые в том или ином виде иногда и в действующей НТД. Таким образом, по передаточной функции могут быть определены частотные характеристики, установленные в действующей НТД. По нормированной передаточной
функции можно определить и время установления выходного сигнала (показания) tr СИ при
скачкообразном изменении измеряемой величины. Действительно, по функции G(jw)
можно найти импульсную переходную характеристику СИ - формула (2.28) - g(t) = По переходной характеристике, задаваясь наибольшим допускаемым отклонением eр выходного сигнала СИ от установившегося значения, можно определить время tr. Пусть, например, СИ является звеном первого порядка. Тогда
Переходная характеристика такого СИ имеет вид Отсюда нетрудно определить Таким образом, по передаточной функции могут быть найдены все характеристики, отражающие динамические свойства СИ в действующей НТД. В отличие от описанных выше полных динамических характеристик, по частным динамическим характеристикам нельзя вычислить динамическую составляющую погрешности измерений. Используя их, можно лишь ориентировочно сопоставить свойства СИ с условиями измерений. В некоторых случаях достаточно нормировать частные динамические характеристики. Например, для стрелочных приборов, предназначенных для измерений постоянных или очень медленно меняющихся величин, указания времени реакции достаточно для того, чтобы указать оператору время считывания показаний при подаче измеряемой величины на вход прибора. Для цифроаналоговых преобразователей (ЦАП) и многозначных управляемых мер, которые, по существу, также являются ЦАП, может нормироваться переходная характеристика или время реакции, поскольку при использовании этих СИ обычно необходимо знать, через какое время после подачи сигнала управления и запуска можно считывать установившееся значение выходной величины. Особую группу СИ составляют аналого-цифровые преобразователи (АЦП), у которых выходной сигнал изменяется дискретно в темпе запуска. Обычно АЦП проектируют так, чтобы все переходные процессы во входных цепях и процесс преобразования заканчивались за время, которое меньше интервала времени между двумя измерениями при максимальном темпе измерений. Поэтому и для этих СИ часто достаточно нормировать время реакции. При длительных переходных процессах во входных цепях (например, при наличии фильтров), когда время реакции АЦП больше интервала времени между двумя измерениями, соответствующего максимально возможной для АЦП данного типа частоте (скорости) измерений, в качестве динамических характеристик подобных АЦП целесообразно нормировать динамические характеристики эквивалентной аналоговой части АЦП, т. е. такие же, как для аналоговых СИ. Кроме того, важной характеристикой является характеристика неопределенности соответствия значения измеряемой величины, зафиксированного в выходном коде, тому моменту времени, который приписывается полученному значению кода. Для АЦП различного принципа действия эта неопределенность (погрешность датирования отсчета) должна отсчитываться от момента запуска. В погрешность датирования отсчета, иногда называемую апертурным временем, может входить время задержки запуска, время автоматического выбора полярности и пределов измерения, время преобразования и т. д. В частном случае, когда на входе АЦП имеется устройство выборки и запоминания, погрешность датирования отсчета будет определяться только временем задержки запуска и динамическими параметрами этого устройства. Определенная таким образом погрешность датирования отсчета представляет собой характеристику, необходимую для метрологического анализа ИС, в которые входит АЦП. Заметим, что при работе АЦП в составе системы, его связь с ЭВМ осуществляется с помощью программ и специальных устройств, вызывающих задержку запуска АЦП. Рис. 8. Возникновение динамической составляющей погрешности измерений в результате наличия погрешности датирования отсчета АЦП. Рассмотрим происхождение
динамической составляющей погрешности измерений Ddyn из-за наличия погрешности
датирования отсчета (рис.
8). На этом рисунке x(t)
- изменяющаяся во времени измеряемая величина; t1, t2, … , t8 - моменты
запуска АЦП, привязанные к оси времени (например, с помощью программируемого
таймера в ИС). Из-за наличия погрешности датирования отсчета Отметим, что при постоянной во времени измеряемой величине описанная составляющая погрешности будет отсутствовать. Легко видеть, что погрешность датирования отсчета не является временем чистого запаздывания, поскольку, по определению МЭК, время чистого запаздывания - это задержка начала реагирования СИ на скачкообразное изменение входного сигнала. Вследствие того, что погрешность датирования отсчета у одного экземпляра АЦП может не быть постоянной (например, может зависеть, от измеряемой величины, может быть переменной во времени и т. п.), при нормировании целесообразно указывать ее статистические характеристики. 2.4. Взаимодействие между объектом измерений и СИ.Известно, что одним из важных процессов, влияющих на погрешность измерений, является взаимодействие между объектом измерения и соединенными с ним СИ, а также между двумя (или более) СИ, последовательно соединенными в ИС. Потребление энергии или мощности СИ от объекта измерения или от предвключенного СИ проводит к изменению значения величины, подлежащей измерению, и следовательно, к появлению соответствующей составляющей погрешности измерений. В настоящее время это явление хорошо изучено и отражено соответствующими характеристиками в действующих НТД лишь в отношении СИ электрических и радиотехнических величин. Однако оно имеет большое значение и для многих СИ других физических величин. Например, на погрешность измерения температуры каких-либо объектов при помощи термопар или термометров сопротивления существенно влияет обмен тепловой энергией между объектом измерения и соответствующим преобразователем температуры. Этот обмен может быть двусторонним. Подсоединение термопары к объекту с малой теплоемкостью может привести к настолько существенному понижению температуры объекта, что пренебречь им при оценке погрешности измерений нельзя. При подсоединении к объекту термометра сопротивления температура объекта может как понижаться вследствие отбора термометром энергии от объекта, так и повышаться, поскольку термометр сопротивления имеет собственный начальный нагрев, и при достаточно большой собственной мощности нагрева может отдавать энергию объекту. Так же обстоит дело с любыми СИ, при работе которых происходит обмен энергии с объектом измерения, с предвключенным, с послевключенным СИ или другим устройством. Таким образом, для СИ, работа которых характеризуется обменом энергией между ними и подключенными к их входу или выходу объектами, необходимо нормировать некоторые характеристики, отражающие свойство СИ отбирать или отдавать энергию через свои входные и выходные цепи. Такие характеристики часто называют импедансами. Нормирование входных и выходных импедансов СИ электрических величин не является новым. При нормировании их необходимо большее внимание обращать на то, чтобы нормируемые характеристики действительно позволяли оценивать соответствующую составляющую погрешности измерений и погрешности ИС. Сложнее обстоит дело с СИ неэлектрических величин. В этой области явление обмена энергией, входные и выходные импедансы СИ изучены недостаточно, поэтому может оказаться, что при разработке способов нормирования и контроля входных и выходных импедансов конкретных видов и групп СИ различных неэлектрических величин потребуется проводить теоретические и экспериментальные исследования для установления наиболее целесообразных способов выражения и методов контроля данных характеристик. Взаимодействия СИ между собой и объектами измерений, вызывающие изменения измеряемых или воспроизводимых величин, могут носить и другой характер. Например, при соединении между собой нескольких концевых мер длины общая длина соединения не будет точно равна сумме длин всех мер, участвующих в соединении. При радиотехнических измерениях на СВЧ волноводные соединения могут вызывать изменения параметров электромагнитных колебаний в линии. Аналогичные искажения электромагнитных колебаний могут вызываться и коаксиальными соединениями. Во всяком случае взаимодействия между СИ, а также взаимодействия СИ с объектами измерений, вызывающие изменения измеряемых величин, могут быть самыми разнообразными. Поэтому необходимо нормировать MX СИ, отражающие способность СИ к подобным взаимодействиям. Необходимо исследовать данные свойства СИ, так как при отсутствии НМХ, отражающих эти свойства СИ, невозможно полностью решить задачу об оценке инструментальных составляющих погрешностей измерений и погрешностей ИС. 2.5. Неинформативные параметры выходного сигнала.Неинформативные параметры выходного сигнала СИ не являются, строго говоря, MX - они определяют рабочую область значений тех параметров выходного сигнала, которые не содержат непосредственной информации о значении измеряемой величины. Однако они определяют возможность нормальной работы СИ и других устройств, подключаемых к выходу данного СИ. Например, выходным сигналом преобразователя напряжения в среднюю частоту следования импульсов является последовательность импульсов. Для определения значения измеряемого напряжения к выходу преобразователя подключают частотомер. Для его нормальной работы необходимо, чтобы амплитуда и форма импульсов преобразователя, хотя они и не несут информации о значении измеряемого напряжения, удовлетворяли определенным требованиям. В противном случае частотомер будет измерять частоту следования этих импульсов с большой погрешностью или вообще перестанет реагировать на эту последовательность импульсов. Неинформативные параметры выходного сигнала преобразователя должны определять допускаемые границы амплитуды и формы импульсов. Аналогичная ситуация характерна для многих измерительных преобразователей. 3. ОСНОВЫ ВЫБОРА КОМПЛЕКСОВ НМХ СИ.Как неоднократно подчеркивалось выше, основное требование к НМХ СИ, положенное в основу ГОСТ 8.009-84, - обеспечение возможности оценки характеристик инструментальной составляющей погрешности измерений по НМХ СИ при известных характеристиках условий применения СИ (влияющих величин) и характере изменений измеряемых величин (частотный спектр). Практически эта оценка может производиться лишь тем или иным объединением отдельных составляющих инструментальной составляющей погрешности измерений. Чрезвычайно большое разнообразие видов и групп СИ делает невозможной регламентацию конкретных комплексов MX для каждого из видов и групп СИ в одном документе. Вместе с тем регламентировать для всех СИ единый комплекс НМХ было бы также неправильно, поскольку, с точки зрения выполнения основного требования к НМХ, все СИ не могут характеризоваться единым комплексом НМХ, даже если он представлен в самой общей форме. Изучение вопроса о рациональной классификации СИ по комплексам НМХ, общим для каждой классификационной группы, при условии что сами эти группы также должны быть достаточно общими, привело к следующему выводу. С одной стороны, такие общие группы в принципе выделить можно. Для этих групп СИ могут быть назначены общие комплексы НМХ. Однако вследствие весьма широкого разнообразия назначений и условий применения СИ при практическом отнесении того или иного типа СИ к одной из выделенных групп неизбежны затруднения и исключения. Тем не менее можно дать некоторые рекомендации по группированию СИ при нормировании MX. Основным признаком разделения СИ на подобные группы является тот общий комплекс НМХ, который необходим в каждой группе для определения инструментальных составляющих погрешностей измерений или MX ИС, характерных для данной группы. С этой точки зрения СИ могут быть разделены на две общие группы: 1. СИ, используемые совместно с другими устройствами, т. е. такие, к выходу которых могут быть подсоединены другие СИ, ЭВМ, печатающие машинки, регулирующие устройства и т. п. К этой группе СИ относятся измерительные преобразователи и меры; 2. СИ, используемые отдельно, т. е. такие, к выходу которых не могут быть подсоединены другие устройства. К ним относятся показывающие измерительные приборы, имеющие шкалу или другое отсчетное устройство и не имеющие другого выхода, а также регистрирующие измерительные приборы. Для большей конкретизации даже общих подходов СИ первой группы оказывается целесообразным разделить еще на две группы, комплексы MX для которых удобно рекомендовать по отдельности. Это измерительные преобразователи и меры (включая ЦАП). Тогда СИ разделяются на три функциональные группы (их удобно расположить по степени усложнения комплексов НМХ): 1) меры и ЦАП; 2) измерительные (и регистрирующие) приборы; 3) измерительные преобразователи. Для СИ третьей группы в отличие от первой и второй групп, должны нормироваться: номинальная функция преобразования (в СИ второй группы ее заменяет шкала или другое градуированное отсчетное устройство); полные динамические характеристики. Для третьей и первой групп СИ в отличие от второй должны нормироваться: характеристики взаимодействия СИ с устройствами, подключаемыми к выходу СИ; неинформативные параметры выходного сигнала. Перечисленные характеристики для СИ второй группы не имеют смысла, за исключением регистрирующих измерительных приборов, для которых целесообразно нормировать полные динамические характеристики. Целесообразно остановиться на полных динамических характеристиках, так как положение с остальными характеристиками, по-видимому, не вызывает вопросов. Полная динамическая характеристика определяет функцию связи между изменяющимися во времени информативными параметрами входного и выходного сигналов. Она удобна для расчетов погрешности первичных или промежуточных преобразователей, работающих в ИС как динамические звенья. Для показывающих измерительных приборов со шкалой или с другим устройством визуального отсчета показание не может фиксироваться, если оно быстро изменяется во времени, поэтому для данных СИ полные динамические характеристики не имеют практического смысла. Для подобных СИ регламентируются частные динамические характеристики. Что касается регистрирующих измерительных приборов, то их выходной сигнал может представлять собой график, отражающий изменение во времени измеряемой величины. Для оценки отличия этого графика от действительного изменения во времени измеряемой величины, т. е. для оценки динамической погрешности подобного регистрирующего измерительного прибора, необходима его полная динамическая характеристика. Как было отмечено, нормирование MX СИ должно обеспечить возможность оценки по НМХ СИ характеристик отдельных составляющих инструментальной составляющей погрешности измерений в такой форме, чтобы их можно было статистически объединять. Однако нельзя исключать из рассмотрения такие СИ, при применении которых статистическое объединение отдельных составляющих инструментальной составляющей погрешности измерений не вызывается необходимостью и, следовательно, приводит к неоправданному усложнению нормирования MX и методик оценки погрешности измерений. Такими СИ являются, например, лабораторные СИ, измеряющие весьма медленно изменяющиеся величины в условиях, близких к нормальным, а также большинство таких образцовых СИ, при использовании которых не производят многократные наблюдения с усреднением результатов. К ним могут быть отнесены также и некоторые промышленные показывающие измерительные приборы, измеряющие весьма медленно изменяющиеся величины в достаточно стабильных внешних условиях (которые целесообразно принять за нормальные) или в условиях, когда изменения внешних влияющих величин вызывают пренебрежимо малые изменения MX СИ. Общим для этих СИ является то обстоятельство, что при оценке инструментальной составляющей погрешности измерений, производимых с их помощью, не требуется применять статистические методы объединения ее отдельных составляющих. За погрешность таких СИ в рабочих условиях может быть принята их основная погрешность или величина, определяемая как арифметическая сумма наибольших возможных значений отдельных составляющих погрешности СИ. Последнее, очевидно, допустимо тогда, когда получаемая таким образом сумма не превышает наибольшей допускаемой инструментальной составляющей погрешности измерений при использовании данных СИ и, следовательно, подобная оценка не приводит к необоснованным выводам о том, что применяемый тип СИ недостаточно «точен» для выполнения тех измерений, для которых он предназначен. Для подобных СИ, как правило, приемлемы в основном способы нормирования MX, регламентируемые традиционно. Необходимо отметить, что арифметическое суммирование наибольших возможных значений отдельных составляющих, при котором в качестве НМХ СИ используются пределы допускаемых основной и дополнительных погрешностей СИ и наибольшее возможное значение динамической погрешности СИ (иногда оно может быть определено по частной нормированной динамической характеристике СИ), приводит к получению интервала суммарной инструментальной составляющей погрешности измерений, которому неизбежно следует приписать вероятность нахождения в нем инструментальной составляющей погрешности измерений, равную единице. Важно отметить, что оценка инструментальной составляющей погрешности измерений путем арифметического суммирования наибольших возможных значений ее составляющих обязательно дает интервал с вероятностью, равной единице, хотя об этом предпочитают умалчивать и практически никогда это не указывают. Статистическое же объединение позволяет оценить интервал с любой требуемой вероятностью. Казалось бы, получение интервала погрешности с вероятностью, равной единице, предпочтительно. Однако интервал с этой вероятностью практически представляет собой грубую оценку сверху искомого интервала погрешности, охватывающую все возможные, в том числе весьма редко реализующиеся, значения погрешности. В действительности, для подавляющего большинства измерении реализация такой наибольшей возможной погрешности практически невероятна, так как практически невероятно одновременное появление всех составляющих погрешности СИ с одинаковым знаком и наибольшими допускаемыми для них значениями. Поэтому требование расчета интервала погрешности, соответствующего вероятности, равной единице, приводит к существенному, часто практически неоправданному ужесточению требований к MX СИ. Такое требование следует предъявлять к наиболее ответственным измерениям, например, связанным со здоровьем и жизнью людей, с возможностью катастрофических последствий неверных измерений и т. п. Арифметическое суммирование наибольших возможных значений составляющих инструментальной составляющей погрешности измерений следовательно, включение в комплекс нормируемых MX СИ пределов допускаемой погрешности СИ, а не ее статистических моментов, допустимо также для СИ, применяемых в условиях, когда число этих составляющих, каждая из которых определяется по отдельной НМХ СИ, не превышает трех. В этом случае расчетные оценки инструментальной составляющей погрешности измерений, полученных арифметическим суммированием наибольших возможных значений ее составляющих и полученные статистическим суммированием характеристик составляющих (при вероятности, хотя и меньшей, но достаточно близкой к единице), практически различаться не будут. Именно этим обусловлены отмеченные выше исключения, когда возможно нормирование не статистических моментов составляющих основной погрешности СИ и других MX СИ, допускающих статистическое объединение составляющих инструментальной составляющей погрешности измерений, а пределов допускаемых значений основной и дополнительной погрешностей СИ: лабораторные СИ, некоторые образцовые СИ, некоторые рабочие показывающие измерительные приборы и т. п. Таким образом, можно выделить две группы MX СИ: 1-я позволяет рассчитывать интервал инструментальной составляющей погрешности измерений, соответствующий заданной вероятности, хотя и близкой, но меньшей единицы; 2-я позволяет рассчитывать наибольший возможный интервал инструментальной составляющей погрешности измерений, в котором она находится с вероятностью, равной единице. Вместе с тем даже при выделении трех указанных выше групп СИ и двух групп MX СИ полностью однозначно рекомендовать комплекс НМХ в каком-либо общем нормативном документе не представляется возможным, так как необходимо учитывать различные конкретные свойства определенных типов СИ и некоторые другие факторы. Поэтому для каждого конкретного типа СИ необходимо устанавливать комплекс НМХ с учетом соображений, изложенных выше. При этом следует руководствоваться более конкретными указаниями и рекомендациями, излагаемыми в ГОСТ 8.009-84 и разд. 6 настоящего методического материала. Могут встретиться случаи, когда НМХ, регламентированных в ГОСТ 8.009-84, будет недостаточно для оценки инструментальной составляющей погрешности измерений с требуемой достоверностью. Для этих случаев предусмотрена возможность нормирования дополнительных к установленным в ГОСТ 8.009-84 MX. 4. ОСНОВЫ ОПРЕДЕЛЕНИЯ ИНСТРУМЕНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ В РЕАЛЬНЫХ УСЛОВИЯХ НА НМХ СИ.По ГОСТ 8.009-84 погрешность СИ в реальных условиях применения может не нормироваться. Это вызвано тем, что отдельные экземпляры СИ одного и того же типа могут применяться в резко различающихся условиях, хотя и лежащих в пределах нормированных для них рабочих условий. Нормирование при такой ситуации погрешности СИ в заданных предельных рабочих условиях привело бы к тому, что нормированное значение в подавляющем большинстве случаев намного превышало бы действительное значение погрешности СИ в реальных условиях их применения. Надо отметить, что имеются предложения (например, рекомендация Подкомитета 13 с МЭК - публикация 359, 1971 г.) о нормировании пределов погрешности СИ для всех значений влияющих величин, т. е. о нормировании погрешности СИ в рабочих условиях применения. Однако если это понимать как нормирование погрешности в худших условиях, то это приведет к последствиям, указанным выше. Если же это понимать как нормирование, определяющее погрешность СИ в любых реальных условиях в пределах рабочих условий применения, то это может привести к чрезвычайно большой трудоемкости испытаний. Поэтому для общего случая в ГОСТ 8.009-84 предусмотрено нормирование MX СИ, позволяющих найти отдельные составляющие погрешности СИ в реальных условиях их применения. При рассмотрении вопроса об определении инструментальной составляющей погрешности измерений в реальных условиях применения СИ необходимо остановиться на том, кто, когда и по каким данным должен это определение проводить. При разработке ГОСТ 8.009-84 исходили из того, что это определение может проводить только потребитель, так как он знает реальные условия применения применяемых им СИ. Во избежание недоразумений уточним, кто понимается здесь под термином «потребитель». Технические измерения характеризуются, как правило, тем, что их проводят по заранее установленным методикам заранее выбранными СИ. Эти методики и применяемые СИ регламентированы в различных документах: в проектах технологических процессов, проектах предприятий и объектов, технологических картах, методиках контроля изделий и т. п. Эти документы разрабатываются по заданным исходным данным: наибольшей допускаемой погрешности измерений; известным с большей или меньшей конкретностью условиям применения СИ; виду, характеру и диапазону изменений измеряемых величин. Оператор, проводящий измерения (если измерения проводятся с участием оператора) или принимающий решения по результатам измерений, действует по установленным в документах правилам. При технических измерениях в его функции не входит оценка погрешностей измерений и их учет. Методика измерений и применяемые СИ, регламентированные в соответствующих документах, должны быть такими, чтобы погрешность измерений не превышала заданного наибольшего допускаемого значения с заданной вероятностью. Правила, которыми руководствуется оператор при принятии решений по результатам измерений, учитывают, что погрешности измерений могут лежать в пределах допускаемых значений с известной вероятностью. Очевидно, что в данной ситуации потребителями СИ, т.е. лицами, выбирающими СИ, оценивающими погрешности измерений, решающими вопрос о выборе схемы и методики измерений и т. п., являются не операторы, непосредственно производящие измерения и принимающие конкретные решения по их результатам, а разработчики технологических процессов, проектов предприятий и объектов, методов испытаний и контроля качества изделий и т. п. Именно они и понимаются под термином «потребитель». Необходимо отметить, что специалисты, разрабатывающие НТД на методики измерений, по выбору СИ, методам оценки погрешностей измерений и т.п., должны обладать весьма высокой квалификацией и большим опытом. Они должны учитывать разнообразные и иногда трудно поддающиеся учету факторы, влияющие на погрешность измерений. Кроме того, следует учитывать, что оценки погрешностей измерений всегда бывают приближенными, и на погрешности измерений могут влиять какие-то факторы, изменяющиеся в процессе проведения измерений. Если возможно, то практически всегда целесообразно экспериментально проверять правильность или степень надежности оценок погрешностей измерений, получаемых при использовании регламентированных методов определения этих оценок, для реальных условий осуществления регламентированных методик измерений. Подобная экспериментальная проверка должна проводиться на стадии разработки соответствующих НТД до их окончательного утверждения. Если экспериментальная проверка невозможна, необходимо каким-либо другим способом контролировать допустимость использования в конкретных случаях методик измерений и методов оценки погрешности измерений, установленных соответствующими НТД. Таким образом, инструментальную составляющую погрешности технических измерений потребитель оценивает по известным ему реальным условиям и режиму эксплуатации СИ и по MX СИ, нормированным в технических условиях на СИ данного типа. Эти оценки потребитель проводит, пользуясь методами, которые, в свою очередь, должны быть регламентированы в НТД и (или) в эксплуатационных документах на СИ данного типа. Конкретные методики оценки погрешности СИ данного типа должны быть установлены разработчиками СИ, поскольку они зависят от свойств СИ данного конкретного типа. Рассмотрим общий подход к оценке характеристик инструментальных составляющих погрешностей измерений на НМХ СИ, которым следует руководствоваться при установлении конкретных методик подобных оценок. Как отмечалось выше, инструментальная составляющая погрешности измерений состоит из основной, дополнительной и динамической погрешностей СИ и погрешности, обусловленной взаимодействием СИ с объектом измерений. Эти составляющие образуют инструментальную составляющую погрешности измерений в реальных условиях. Поскольку эта составляющая погрешности измерений, как указано выше в разд. 1, 2, является случайной, то определить ее - значит найти интервал, в котором с заданной вероятностью Р находится погрешность. Этот интервал можно оценивать, например, в три этапа: 1) определение математического ожидания М[Di] и дисперсии D[Di] каждой из четырех составляющих; 2) определение математического ожидания М[Dinstr] и дисперсии D[Dinstr] инструментальной составляющей погрешности измерений: 3) оценка интервала, в котором с вероятностью P лежит инструментальная составляющая погрешности измерений:
где
К - коэффициент, зависящий от вида закона распределения погрешности и от заданной вероятности P. На первом этапе математическое
ожидание и дисперсия основной погрешности D0 СИ
определяются по математическому ожиданию M[Dos] и дисперсии D[Dos] систематической
составляющей, по дисперсии
Естественно, что при отсутствии нормирования некоторых членов формулы (4.3), их принимают равными нулю, так как отсутствие нормирования какой-либо характеристики СИ означает, что для СИ данного типа эта характеристика пренебрежимо мала. * Автокорреляционная функция (спектральная плотность) используется при условиях, указанных на с. 61, 62, 105, 106. Несколько сложнее обстоит дело с оценкой математического ожидания и дисперсии дополнительной погрешности, поскольку для этого необходимо знать не только нормированные вид и коэффициенты функции влияния Y(x), но и статистические характеристики аргументов этой функции - влияющих величин x. Для полевых и промышленных условий могут быть установлены типичные характеристики условий применения для различных групп предприятий. В частности, в ГОСТ 16350-80 определены статистические характеристики климатических условий для различных зон территории СССР. Во всяком случае некоторые характеристики реальных условий применения СИ в том или ином виде должны быть известны потребителю. От того, какие характеристики реальных условий применения СИ потребителю известны, зависят достоверность получаемых им оценок инструментальной составляющей погрешности измерений. При рассмотрении функций влияния были изложены соображения и правила, которыми следует руководствоваться при оценке математического ожидания и дисперсии дополнительной погрешности. Если для СИ нормированы функции влияния Yi(xi) каждой влияющей величины xi отдельно, то математическое ожидание и дисперсия суммарной дополнительной погрешности М[Y(x)] и D[Y(x)] определяются как
где l - число внешних влияющих величин x. Если же нормирована функция совместного влияния нескольких влияющих величин Y(x1, x2, … , xl), то ее математическое ожидание и дисперсию находят по известным правилам определения статистических характеристик функций нескольких случайных величин. Таким образом определяют математическое ожидание и дисперсию функций влияния на те характеристики погрешности СИ, для которых они нормированы в НТД на СИ. Необходимо отметить, что если функция влияния на случайную погрешность нормируется в виде функции влияния на среднее квадратическое отклонение случайной погрешности, а не на дисперсию, то выделять отдельно дисперсию этой функции нецелесообразно. В этом случае следует пользоваться дисперсией, равной квадрату суммы среднего квадратического отклонения случайной составляющей основной погрешности и максимального значения функции влияния на среднее квадратическое отклонение случайной составляющей погрешности - см. формулы (2.19) и (2.20). Далее следует определить математическое ожидание и дисперсию динамической погрешности СИ при известном характере изменения измеряемой величины. Выше при рассмотрении динамических характеристик был описан общий подход к определению динамических погрешностей. Для трех часто встречающихся видов измеряемой величины были определены математическое ожидание M[Ddyn] (в рассмотренных случаях равные нулю) и дисперсия D[Ddyn] динамической составляющей погрешности - см. формулы (2.43), (2.45) и (2.48). Конкретные способы оценки составляющих, обусловленных взаимодействием СИ с объектом измерений, зависят от характера этого взаимодействия и от вида характеристики СИ, отражающей его способность к взаимодействию. В распространенном случае, когда взаимодействие заключается в потреблении энергии СИ от объекта измерений и когда соответствующее свойство СИ отражается его входным импедансом, составляющая погрешности измерений Den, обусловленная этим взаимодействием, может быть найдена следующим образом. Пусть величина, подлежащая измерению, есть Х(jw), а выходной импеданс объекта измерений, включая импеданс линии связи объекта с СИ, - Zout(jw). На вход СИ будет поступать величина
где Zin(jw) - входной импеданс СИ. Составляющая Den = X*(jw) - Х(jw) или Поскольку структура (4.6) подобна структуре (2.42), нетрудно для конкретного вида сигнала Х(jw) получить соотношения, определяющие М[Den] и D[Den], аналогичные подобным соотношениям для динамической погрешности. Например, если Х(jw) - стационарный центрированный случайный процесс, то
где Sx(w) - спектральная плотность процесса Х(jw). Таким образом, закончен первый этап - определены математические ожидания М[Di] и дисперсии D[Di] четырех составляющих инструментальной составляющей погрешности измерений в реальных условиях: основной погрешности D0, дополнительной погрешности (функции влияния Y(x), динамической погрешности Ddyn и погрешности Den, обусловленной взаимодействием СИ с объектом измерений. На втором этапе определяют математическое ожидание и дисперсию инструментальной составляющей Dinstr погрешности измерений в реальных условиях по формулам (4.1). На третьем этапе для оценки интервала, в котором с заданной вероятностью Р находится инструментальная составляющая погрешности измерений в реальных условиях, необходимо выбрать значение коэффициента К. Как отмечалось выше, для его выбора необходимо знать вид закона распределения погрешности Dinstr. Например, если есть основания полагать, что этот закон - нормальный, то известно, что К = 3 при Р = 0,997. Однако во многих случаях допустима достаточно приближенная оценка искомого интервала. Точно эту оценку получить весьма трудно, а в большинстве случаев и не нужно. Тогда, если есть основания полагать, что плотность распределения вероятностей погрешности Dinstr - усеченная, одномодальная, симметричная функция, находящаяся в широкой области плотностей распределения от равномерной до весьма «острой» (см. рис. 9), можно выбрать значение коэффициента Kcp по графику, показанному на рис. 10 [6]. Этот график показывает зависимость от вероятности Р среднего значения коэффициента K для данной группы плотностей распределения. На рис. 10 заштрихована область возможных действительных функций зависимости К от Р. При увеличении вероятности отклонение границ этой области от Кcр возрастает, так что при Р = 0,95 погрешность коэффициента К лежит в границах ± 16 %, а при Р = 0,99 - в границах ± 30 %. Нередко проводят измерения, окончательным результатом которых является результат математической обработки значений выходных сигналов измерительных преобразователей. В таких случаях погрешность измерений зависит от вида математической обработки и некоторых MX СИ, которые выше в расчет инструментальной составляющей погрешности измерений не входили. Рис. 9. Типовые функции плотности распределения вероятностей погрешности. Рис. 10. Зависимость коэффициента К от вероятности Р. Часто встречающийся вид математической обработки наблюдений - вычитание. Он применяется при определении зависимости свойств каких-либо объектов от изменений некоторых влияющих факторов, т. е. при разнообразных испытаниях материалов, изделий и т. п. Например, при испытаниях механических свойств материалов определяют зависимость деформации образца материала от приложенной к нему механической нагрузки. При этом измеряют размер x1 образца при некоторой нагрузке F1, затем прикладывают другую нагрузку F2 и измеряют изменившийся размер х2. Определяемое свойство образца характеризуется разностью x2 - x1, полученной при данной разности F2 - F1. По такой же схеме проводят и многие другие испытания. Погрешность измерения в данном случае есть погрешность измерения разности z = x2 - x1. (4.8) Математическое ожидание и дисперсия погрешности Dz этой разности, как известно, определяются по формулам где Dx1, Dx2, Dz - погрешности
измерений величин x1;
x2, z, соответственно; В простейшем случае в качестве погрешностей Dx можно принять основную погрешность СИ. Тогда формулы (4.9) можно записать в виде где
В (4.10) предполагается, что автокорреляционная функция погрешности СИ одна и та же в точках диапазона измерений x1 и x2. Зависимость МХ М[Dx] и D[Dx] от точки диапазона измерений в соответствии с ГОСТ 8.009-84 нормируется. Если при испытаниях значение x2 мало отличается от x1, то формулы (4.10) можно записать в виде
или где
- нормализованная автокорреляционная функция основной погрешности СИ. Из
(4.12)
видна целесообразность учета при подобных измерениях автокорреляционной функции
погрешности СИ и, следовательно, необходимость ее нормирования. Если функцию В любом случае, когда математической обработке любого вида подвергают результаты отдельных наблюдений, проводимых последовательно во времени, учет автокорреляционной функции погрешности СИ позволяет уточнить оценку погрешности измерений. Учитывать
автокорреляционную функцию необходимо также при определении дисперсии или
среднего квадратического отклонения погрешности СИ в процессе испытаний СИ.
Определяя среднее квадратическое отклонение случайной составляющей погрешности
по общеизвестным формулам, например, по формулам (4) и (4а)
приложения 2 к ГОСТ 8.009-84, необходимо обеспечить при
эксперименте независимость отдельных наблюдений Di. С этой целью интервал времени между отдельными
наблюдениями должен быть не меньше интервала корреляции случайной составляющей
погрешности СИ (интервал корреляции - такое значение аргумента t, при котором функция Рекомендовать конечное число определенных расчетных формул, применимых для оценки инструментальной составляющей погрешности измерений для всех возможных условий, видов и методик измерений вряд ли возможно. В каждом конкретном случае необходимо учитывать все существенно влияющие факторы. В настоящем методическом материале определен общий подход к расчету инструментальной составляющей погрешности измерений. Более конкретные рекомендации по расчету погрешности СИ в реальных условиях применения даны в РД 50-453-84 «Методические указания. Характеристики погрешности средств измерений в реальных условиях эксплуатации. Методы расчета». 5. ПОДХОД К ВЫБОРУ КОМПЛЕКСА НМХ И ЗНАЧЕНИЙ НОРМ.Разработка любых СИ начинается с определения их назначения и условий применения. Во многих случаях этих данных достаточно для того, чтобы однозначно определить необходимый комплекс НМХ СИ. Однако иногда заданные назначение и условия применения СИ достаточно широки и разнообразны. Тогда разработчик должен проанализировать возможные способы нормирования MX для различных предусмотренных назначений и условий применения СИ, а также трудоемкость контроля характеристик при этих способах нормирования. В результате анализа может оказаться, что нормирование наиболее представительного комплекса характеристик, требующего особенно трудоемкого контроля, для всех СИ данного типа экономически нецелесообразно. Тогда могут быть предусмотрены их модификации, каждая из которых имеет более узкое назначение и условия применения, чем тип СИ в целом. При этом они могут различаться только комплексами НМХ. Вопрос о комплексе НМХ данного типа СИ должен решаться на стадии технического задания на разработку СИ. Однако не исключено, что по окончании разработки, после испытаний опытных образцов СИ окажется целесообразным изменить НМХ СИ. Например, в результате испытаний опытных образцов СИ, для которого первоначально были нормированы функции влияния и передаточная функция, может оказаться, что MX данного СИ таковы, что погрешности измерений, осуществляемых при его помощи, мало зависят от возможных реальных изменений влияющих величин, а также от скорости (частоты) изменений измеряемой величины в пределах возможных реальных значений. Поэтому целесообразно с целью упрощения нормирования MX и их контроля вместо функций влияния и передаточной функции нормировать наибольшее допускаемое изменение погрешности Dр(x) и амплитудно-частотную характеристику. Окончательное решение этого вопроса должно оставаться за потребителем, утвердившим техническое задание на разработку СИ, и Госстандартом СССР, осуществляющим надзор за качеством выпускаемых СИ. Таким образом, конкретный комплекс MX, нормируемых для данного типа СИ, в первом приближении устанавливают на стадии составления технического задания на разработку СИ. При установлении комплекса НМХ СИ данного типа необходимо исходить, помимо требований приложения 1 к ГОСТ 8.009-84, из общей тенденции ГОСТ 8.009-84 - обеспечения возможности оценки инструментальной составляющей погрешности измерений с достаточной достоверностью по НМХ СИ. При установлении комплекса НМХ для СИ данного типа необходимо учитывать еще одно обстоятельство. Для некоторых СИ может оказаться необходимым нормировать среднее квадратическое отклонение (или дисперсию) случайной составляющей погрешности, но не нужным нормирование ее автокорреляционной функции. Такая ситуация характерна для СИ, обладающих существенной случайной составляющей погрешности, в двух случаях. Во-первых, когда эта составляющая погрешности СИ, являясь случайным процессом, имеет настолько малый интервал корреляции, что погрешности любых двух последовательных наблюдений всегда будут взаимно некоррелированы. Во-вторых, когда случайная составляющая погрешности СИ является случайной величиной, а не случайным процессом. Если приведенная к выходу СИ случайная составляющая погрешности, являясь случайным процессом, обладает весьма малым интервалом корреляции (например, высокочастотный шум), но СИ предназначено для применения в качестве преобразователя в ИС, нормирование автокорреляционной функции погрешности или спектральной плотности является необходимым. Это вызвано тем обстоятельством, что частотный спектр погрешности СИ и в этом случае нужно учитывать при оценке погрешности ИС, в которую данное СИ входит как промежуточный компонент. Далее рассмотрим общие соображения, которыми следует руководствоваться при установлении значений норм на MX СИ. Правильный выбор значений норм оказывает существенное влияние на технико-экономическую эффективность производства СИ данного типа. В терминах статистики тип СИ представляет собой некоторую генеральную совокупность случайных объектов, обладающую определенными свойствами. Этот комплекс свойств генеральной совокупности отражается нормами на MX данного типа СИ. Исходя из этих представлений, операцию установления значений норм для данного типа СИ можно было бы представить следующим образом: 1. Берут достаточно представительную выборку из данной генеральной совокупности. Под выборкой в данном случае следует понимать некоторое число «исправных» экземпляров СИ данного типа. Понятие «исправные» экземпляры СИ в данном случае отличается от общепринятого, поскольку значения норм еще не установлены, и, следовательно, обычные критерии «исправности» пока отсутствуют. Поэтому здесь понятие «исправное» СИ следует понимать в том смысле, что оно соответствует общим свойствам генеральной совокупности или, говоря более конкретно, выбранные «исправные» СИ изготовлены при строгом соблюдении чертежей и требований установленного технологического процесса серийного производства. 2. С помощью принятых в статистике методов проверки статистических гипотез устанавливают такие значения норм, при которых при принятом «уровне значимости» удовлетворяется гипотеза о том, что экземпляры взятой выборки СИ входят в данную генеральную совокупность. При этом можно считать, что установленные таким образом значения норм достаточно хорошо отражают свойства «исправных», т.е. изготовленных в соответствии с чертежами и технологией производства, СИ. Эффективность производства, определяемая возможностью выпуска по чертежам и установленной технологии производства СИ как удовлетворяющих, так и не удовлетворяющих нормам, отражена принятым «уровнем значимости» при проверке гипотезы. Надо отметить, что подобная процедура является одинаково строгой при любых способах нормирования MX СИ. Однако практическая целесообразность применения описанной «строгой» процедуры на стадии разработки СИ вызывает серьезные сомнения. Во-первых, необходимо, как правило, достаточно большое количество «исправных» экземпляров СИ данного типа, во-вторых, описанная процедура весьма трудоемка и с учетом необходимости изготовления дополнительного количества экземпляров СИ приведет к существенному увеличению сроков и стоимости разработок СИ. Нельзя не учитывать то обстоятельство, что принятая в течение многих лет разработок СИ практика установления значений норм MX, не будучи строго научно обоснованной, не приводит, как правило, к существенно неудовлетворительным результатам. Принятую практику установления норм на MX СИ надо было бы признать неудовлетворительной в том случае, если бы она приводила к тому, что при серийном выпуске СИ наблюдался бы или недопустимо большой брак (т. е. слишком большое количество СИ, MX которых при выпуске из производства не удовлетворяют нормам), или слишком большой «запас» по значению MX относительно норм (т. е. большое количество СИ, MX которых при выпуске из производства значительно лучше, чем допускается нормами). В обоих случаях производство СИ было бы недостаточно экономически эффективным. Однако, как известно, при нормально организованном современном производстве подобная ситуация встречается редко. В тех отдельных случаях, когда она наблюдается, производится некоторое уточнение значений норм. На основании изложенного можно сделать вывод, что при установлении значений норм MX, соответствующих ГОСТ 8.009-84, нет причины отказываться от практики, принятой в настоящее время. Эта практика заключается в следующем. В процессе разработки СИ данного типа рассчитывают MX разработанной схемы и конструкции с учетом свойств и технических характеристик примененных материалов, элементов и комплектующих изделий. В результате такого расчета получают ориентировочные значения MX, которые уточняют при экспериментальном исследовании макетов и опытных образцов СИ. Затем на основании опыта и, в известной степени, инженерной интуиции разработчик с учетом известного ему уровня технологии и культуры серийного производства приборостроительных заводов выбирает из числа стандартизированных рядов (если они имеются) значения НМХ, правильность выбора которых контролируют при испытаниях образцов, изготовленных заводом с помощью оборудования и по технологии серийного производства. В отношении MX СИ, регламентируемых ГОСТ 8.009-84, необходимо применительно к рассматриваемому вопросу отметить следующее. ГОСТ 8.009-84 предусматривает более полное отражение свойств СИ, чем традиционно принятое. Поэтому в процессе разработки СИ потребуются более глубокие и детальные исследования свойств разрабатываемых СИ. Сюда, например, относится анализ динамических характеристик, функций влияния и некоторых других характеристик. Однако общий подход и последовательность работы по установлению значений норм на MX СИ целесообразно сохранить такими же, каковы они в настоящее время. Вместе с тем кратко упомянутые выше статистические методы нахождения объективных характеристик генеральной совокупности случайных объектов применительно к СИ весьма перспективны. Они являются инструментом, которым можно управлять эффективностью производства СИ. Вероятно, его целесообразно вводить в действие на той стадии производства, когда технология серийного производства СИ данного типа достаточно хорошо отработана и уже выпущено достаточно большое количество экземпляров СИ, MX которых регистрировались заводом-изготовителем перед отправлением СИ потребителям. Тогда, задаваясь необходимой эффективностью производства (допускаемой долей возврата СИ, забракованных при контроле, и целесообразным «запасом» MX выпускаемых СИ относительно норм), в принципе можно, пользуясь накопленными статистическими данными, установить соответствующие уточненные значения норм. В связи с этим необходимо обратить внимание на следующую характерную особенность двух. MX, регламентируемых в ГОСТ 8.009-84. М[Dos] и s[Dos] обладают существенной особенностью по сравнению с другими нормируемыми характеристиками СИ. Все остальные характеристики отражают свойства не только типа в целом, но и каждого отдельного экземпляра СИ данного типа, а характеристики М[Dos] и s[Dos] - свойства всей совокупности СИ данного типа в целом. По таким характеристикам нельзя определить исправность или неисправность СИ, поэтому они не могут служить критерием допустимости выпуска СИ в обращение или в эксплуатацию. Для потребителей они дают информацию о характере группирования систематических погрешностей СИ данного типа и позволяют обоснованно рассчитывать инструментальную составляющую погрешности технических измерений. Кроме того, они в некоторой степени отражают качество технологического процесса изготовления СИ, поэтому, если при контроле характеристик М[Dos] и s[Dos] окажется, что они не соответствуют установленным нормам в худшую сторону, следует обратить внимание завода-изготовителя на ухудшение качества технологического процесса. Когда же полученные при контроле характеристики существенно лучше установленных норм, то в технические условия и сопроводительную документацию должны быть внесены соответственно измененные значения М[Dos] и s[Dos]. Таким образом, регламентируемые в НТД значения М[Dos] и s[Dos] не являются жесткими нормами, определяющими качество отдельных экземпляров СИ, а представляют собой ориентировочные значения, приближенно характеризующие совокупность СИ данного типа. Поэтому эти характеристики на стадии разработки СИ можно определять не обязательно путем строгих статистических испытаний представительной выборки СИ данного типа, а приближенным анализом систем допусков на полуфабрикаты и комплектующие изделия, технологии изготовления и метода регулирования (градуировки) СИ данного типа. В частности, если есть основания полагать, что систематическая погрешность разных экземпляров СИ данного типа может принимать любое значение в пределах допуска с равной вероятностью, то можно принять, что закон распределения этой погрешности равномерный в пределах допуска ± Dosp и тогда
В дальнейшем в процессе серийного выпуска СИ и накопления статистических данных эти характеристики могут уточняться. 6. УСТАНОВЛЕНИЕ КРИТЕРИЕВ СУЩЕСТВЕННОСТИ СОСТАВЛЯЮЩИХ ПОГРЕШНОСТИ СИ.В ГОСТ 8.009-84 комплекс НМХ для СИ конкретного типа устанавливается на основании принятой для СИ данного типа модели его погрешности в реальных условиях применения. Для соответствующей модели и вида СИ устанавливаются следующие критерии существенности составляющих погрешности СИ: 1. Составляющие основной погрешности для модели I аналоговых СИ и ЦАП. В общем случае наибольшее значение D0max основной погрешности с вероятностью, близкой к единице, может быть определено по формуле Предел Dosp допускаемой систематической составляющей основной погрешности нормируется во всех случаях без исключения. Принимаем, что характеристики случайных составляющих основной погрешности СИ целесообразно нормировать при условии Принимаем, что любой член под корнем в формуле (6.3) считается пренебрежимо малым по сравнению с другим членом под корнем, если он составляет 0,1 другого члена. Следовательно: а) вариация Н0
считается пренебрежимо малой по сравнению с б) Характеристики Это означает, что если
характеристики случайных составляющих основной погрешности СИ нормироваться
должны, то при соблюдении условия (6.6) следует нормировать и Теперь рассмотрим критерии целесообразности нормирования характеристик случайных составляющих основной погрешности СИ. За базу принимается критерий (6.2). В случае соблюдения условия (6.4) можно записать
и критерий (6.2) принимает вид
В случае соблюдения условия (6.5) можно записать
и критерий (6.2) принимает вид
В случае соблюдения условия (6.6) e имеет вид (6.3) и критерий (6.2) приводится к виду
Таким образом, критерии рациональности нормирования характеристик случайных составляющих основной погрешности следующие: нормируется при нормируется Н0, а при нормируются и Если не соблюдается любое из
вторых неравенств (6.12) - (6.14) при соблюдении
соответствующих первых неравенств, ни 2. Составляющие основной погрешности для модели I цифровых измерительных и регистрирующих приборов (ЦИП) и АЦП. По аналогии с (6.1) наибольшее значение D0max основной погрешности ЦИП и АЦП c вероятностью, близкой к единице, может быть определено по формуле Так же, как и для аналоговых СИ,
предел Dosp допускаемой
систематической составляющей основной погрешности нормируется во всех случаях
без исключения. Однако для ЦИП и АЦП номинальная ступень квантования qsf (единица
наименьшего разряда кода) также нормируется во всех случаях без исключения
(ГОСТ 14014-82). Вопрос о целесообразности или нецелесообразности нормирования
значения qsf
вследствие ее малости по сравнению с остальными составляющими формулы (6.15)
рассматриваться не может. Существенное превышение слагаемых Такие ЦИП и АЦП не должны выпускаться, и, следовательно, вопрос о нормировании их MX не актуален. Из (6.15) видно, что H0 и qsf влияют на погрешность одинаково. Поскольку qsf нормируется во всех случаях, пользуясь теми же критериями, что в п. 1, будем считать, что вариацию можно считать пренебрежимо малой и не нормировать при соблюдении неравенства Из тех же соображений будем
считать
В случае, если неравенства (6.16) и
(или) (6.17) не соблюдаются, необходимо нормировать Н0 и
(или) Необходимо отметить, что в
данном случае, в отличие от аналоговых СИ, вопрос о нормировании Н0
и 3. Характеристики основной погрешности для модели II аналоговых СИ и АЦП. В случае, если для СИ данного типа нормируется 2-я группа характеристик погрешности (модель II), т. е. основная погрешность СИ нормируется в целом, без разделения ее не составляющие, одновременно с характеристиками основной погрешности часто дополнительно нормируют еще и вариацию Н. Тогда учитывая, что
по аналогии с (6.2) принимаем, что вариация признается существенной и, следовательно, нормируется при соблюдении условия
4. Характеристики основной погрешности для модели II ЦИП и АЦП. Для ЦИП и АЦП можем написать
Учитывая, что, как отмечено в п. 2, значение qsf нормируется всегда, принимаем по аналогии с (6.2), что характеристику случайной составляющей погрешности ЦИП и АЦП, обусловленной гистерезисом, т. е. вариацию, целесообразно нормировать при условии
5. Дополнительные и динамические погрешности СИ. В отношении дополнительных погрешностей СИ может иметь место одно из следующих двух условий: 1) наибольшие значения всех дополнительных погрешностей СИ, возможные при применении СИ в рабочих условиях, примерно соизмеримы между собой. Соизмеримыми здесь считаются погрешности, значения которых различаются не более чем на 30 %; 2) среди дополнительных погрешностей имеются такие, наибольшие возможные значения которых меньше, чем других, более чем на 30 %. Погрешности, значения которых различаются более чем на 30 %, считаются несоизмеримыми. Принимается, что при соизмеримых всех наибольших возможных значениях дополнительных погрешностей эти погрешности считаются существенными при условии, что сумма всех наибольших возможных значений дополнительных погрешностей равна или превышает 0,2 суммы наибольших возможных значений остальных составляющих погрешности СИ в рабочих условиях применения. Это соответствует соблюдению неравенства В случае, если среди наибольших возможных значений дополнительных погрешностей имеются несоизмеримые погрешности, выделяется группа «меньших» погрешностей. В группу «меньших» входят те из дополнительных погрешностей, сумма наибольших возможных значений которых составляет не более 0,2 суммы наибольших возможных значений остальных составляющих погрешности СИ в рабочих условиях применения СИ данного типа. Если такую группу «меньших» погрешностей можно выделить, то они считаются несущественными. Условие, при соблюдении которого эта часть дополнительных погрешностей считается несущественной, записывается в виде
Вопрос о существенности динамических погрешностей СИ решается аналогично вопросу о дополнительных погрешностях. В соответствии с изложенным выше, динамические погрешности считаются существенными при выполнении условия, подобного условию (6.22),
где Принятый здесь подход к установлению критериев существенности составляющих погрешности СИ и сами критерии применимы и для СИ, предназначенных для работы в составе ИС. 7. ПЕРЕХОД ОТ НОВЫХ MX СИ, РЕГЛАМЕНТИРОВАННЫХ В ГОСТ 8.009-84, К ТРАДИЦИОННЫМ MX.В ГОСТ 8.009-84 регламентированы некоторые MX СИ, которые до недавнего времени не нормировались. В большинстве документов рекомендуются для нормирования практически одни и те же традиционные MX СИ. Целесообразно рассмотреть вопрос о связи новых MX, регламентированных в ГОСТ 8.009-84, с традиционными MX. Основные различия ГОСТ 8.009-84 и традиционных документов заключаются в следующем: 1. В ГОСТ 8.009-84 предусмотрено нормирование ряда характеристик основной погрешности СИ, традиционно - только пределы допускаемой основной погрешности. 2. В ГОСТ 8.009-84 предусмотрено нормирование функций влияния, традиционно - пределов допускаемых значений дополнительных погрешностей в виде двузначной (±) зоны, в которой может лежать изменение выходного сигнала (показания) СИ, вызванное определенным значением изменения влияющей величины. 3. В ГОСТ 8.009-84 предусмотрено нормирование полных динамических характеристик СИ, традиционно нормируется так называемое время установления показания или амплитудно- и фазово-частотные характеристики. MX, регламентированные в ГОСТ 8.009-84, более полно и объективно отражают свойства СИ, чем MX, традиционно нормируемые. Между характеристиками, регламентированными в ГОСТ 8.009-84, и основными характеристиками, нормируемыми традиционно, существует известная связь. Зная первые, можно определить вторые (но не наоборот). По указанным трем группам характеристик это можно сделать следующим образом. 1. Пределы допускаемой основной
погрешности ± Dop - это интервал,
в котором находится значение основной погрешности СИ. Если СИ не обладает
случайной составляющей погрешности, т. е. При существенной случайной
составляющей погрешности СИ в состав MX, нормируемых по ГОСТ 8.009-84, помимо пределов допускаемой
систематической составляющей основной погрешности ± Dosp, входит предел
допускаемого среднего квадратического отклонения случайной составляющей
основной погрешности где К - коэффициент, зависящий от принятой вероятности Р. При P =0,96, можно принять К = 2, тогда
При наличии вариации
В тех редких случаях, когда коэффициент К не может быть принят равным двум, соответствующая зависимость К = f(P) все равно должна быть определена разработчиком для данного типа СИ с целью внесения ее в эксплуатационную документацию. Эта зависимость может быть использована и при расчете по формуле (7.1). 2. Функция влияния Y(x) определяет зависимость выходного сигнала (показания) СИ от изменения влияющей величины в пределах заданных рабочих условий применения СИ. Дифференцируя эту функцию, можно найти значение величины x, при котором скорость изменения этой функции максимальна. Тогда легко определить и наибольшее допускаемое изменение выходного сигнала (показания) СИ Dcp, вызываемое изменением Dx величины x
В частности, если функция Y(x) - линейная функция Y(x) = А · x, то Dcp = A · Dx. (7.4) 3. Нормируемые по ГОСТ 8.009-84 полные динамические характеристики СИ всегда могут быть приведены к передаточной функции G(S) или в другом виде записи к амплитудно-фазовой характеристике G(jw). В каком бы виде не нормировалась полная динамическая характеристика СИ, используя известные преобразования (с учетом того, что СИ - линейное звено), ее можно записать (2.29):
Таким образом, по полной динамической характеристике, нормируемой по ГОСТ 8.009-84, определяют частные характеристики, иногда традиционно нормируемые. С другой стороны, в каком бы виде не нормировалась полная динамическая характеристика СИ по ГОСТ 8.009-84, она может быть записана в виде переходной характеристики h(t), представляющей реакцию СИ на ступенчатое изменение входного сигнала. Время установления tr выходного сигнала (показания) СИ определяется как время, в течение которого выходной сигнал (показание) СИ изменится до значения, отличающегося от своего нового установившегося значения на некоторую малую величину vp при ступенчатом изменении информативного параметра входного сигнала от одного постоянного до другого постоянного значения. Зная переходную характеристику h(t), время tr можно определить из уравнения
где h(¥) и h(tr) - значения переходной характеристики при t = ¥ и при t = tr, соответственно. В частном случае (2.51) tr определяются формулой (2.52). Погрешность СИ в рабочих условиях также легко определить по MX СИ, установленном в ГОСТ 8.009-84. Таким образом, по более общим MX СИ, регламентированным в ГОСТ 8.009-84, достаточно просто можно найти любые частные MX, традиционно нормированные как в различных международных рекомендациях, так и в ряде НТД, действующих в СССР. В приложении 2 приведен пример определения НМХ конкретного типа СИ и расчеты но ним характеристик погрешности СИ в реальных условиях применения. ПРИЛОЖЕНИЕ 1
|
|
при uin = 0 |
при uin = 10 мВ |
|
M[D0] = 30 мкВ (0,3 %) |
M[D0] = 60 мкВ (0,6 %) |
|
s[D0] = 45 мкВ (0,45 %) |
s[D0] = 63 мкВ (0,6 %) |
|
M[Dc] = - 15 мкВ (0,15 %) |
M[Dc] = - 30 мкВ (0,3 %) |
|
s[Dc] = 60 мкВ (0,6 %) |
s[Dc] = 87 мкВ (0,9 %) |
|
M[D] = 14 мкВ (0,15 %) |
M[D] = 28 мкВ (0,3 %) |
|
s[D] = 75 мкВ (0,75 %) |
s[D] = 107 мкВ (1,1 %) |
Интервал, в котором находится погрешность усилителя в рабочих условиях применения, может быть выражен как
![]() (44)
(44)
Можно приближенно считать (см. разд. 4 настоящих методических указаний), что погрешность находится в данном интервале с вероятностью ~ 0,96.
Здесь и далее в % даны значения приведенной погрешности при нормирующем значении uin, равном 10 мВ.
При оценке характеристик погрешности СИ в реальных условиях их применения, конечно, необходимо проверить, насколько целесообразно учитывать изменения математического ожидания погрешности во времени. Это, очевидно, зависит от соотношения этих изменений с другими составляющими математического ожидания погрешности, а также с другими характеристиками погрешности с учетом интервала времени между регулировками (коррекциями) дрейфа погрешности СИ, если такие регулировки предусмотрены.
Интересно сравнить полученные результаты (45) с результатами, которые могли бы быть получены при традиционном нормировании MX усилителя. Для этого определим интервал, в котором будет находиться расчетное значение погрешности усилителя в указанных выше условиях, при использовании для расчета традиционно нормируемых характеристик - пределов допускаемых основной погрешности Dop и дополнительных погрешностей Dcp (на единицу изменения влияющей величины).
Примем, что пределы допускаемой основной погрешности выбраны равными
![]() (46)
(46)
Подобное соотношение логично принять потому, что оно определяет интервал, в котором в худшем случае погрешность усилителя в нормальных условиях будет находиться с достаточно большой вероятностью. Тогда в соответствии с принятыми свойствами усилителя можно найти пределы допускаемой основной погрешности, которые традиционно должны были бы нормироваться для усилителя данного типа, см. формулы (17) и (18)
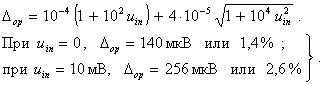 (47)
(47)
Пределы допускаемой дополнительной погрешности должны нормироваться равными - см. формулы (20) и (21)
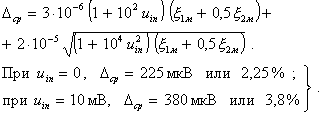 (48)
(48)
Тогда пределы, в которых находится погрешность усилителя в рабочих условиях, определяются по формуле
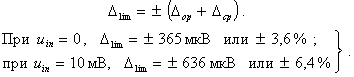 (49)
(49)
Сравнивая (49) и (45), видим, что оценки погрешности усилителя в рабочих условиях получаются значительно лучшими (интервал меньше в 2,5 - 3,0 раза) при использовании для ее расчета НМХ, принятых в рассматриваемом примере, т. е. статистических характеристик основной погрешности и функций влияния, чем при использовании традиционно нормируемых MX.
В примере обозначены:
un - приведенное к выходу напряжение аддитивного шума усилителя;
dn - относительное изменение коэффициента усиления, отражающее мультипликативный шум усилителя;
udr - приведенное к выходу напряжение дрейфа нулевого уровня усилителя;
ddr - относительное изменение коэффициента усиления, отражающее дрейф коэффициента усиления усилителя;
![]() - значение математического ожидания
составляющей напряжения ит, обусловленной собственным прогревом
усилителя, в момент включения усилителя;
- значение математического ожидания
составляющей напряжения ит, обусловленной собственным прогревом
усилителя, в момент включения усилителя;
![]() - значение математического ожидания
составляющей относительного изменения бг коэффициента усиления, обусловленной
собственным прогревом усилителя, в момент включения усилителя;
- значение математического ожидания
составляющей относительного изменения бг коэффициента усиления, обусловленной
собственным прогревом усилителя, в момент включения усилителя;
au, ad - коэффициенты, определяющие скорости изменений математических ожиданий напряжения дрейфа и относительного изменения коэффициента усиления под влиянием собственного прогрева усилителя;
t0 - момент времени последней корректировки погрешности усилителя;
tsw - момент времени включения усилителя;
v1 - математическое ожидание скорости изменения составляющей напряжения udr, обусловленной временным старением элементов усилителя;
v2 - математическое ожидание скорости изменения составляющей относительного изменения ddr коэффициента усиления, обусловленной временным старением элементов усилителя;
R1(t), R1sf(t) - истинная и номинальная автокорреляционные функции стационарной случайной составляющей напряжения иdr, соответственно;
R2(t), R2sf(t) - истинная и номинальная автокорреляционные функции стационарной случайной составляющей относительного изменения ddr, коэффициента усиления, соответственно;
uin - входное напряжение усилителя;
uin.sf - номинальное значение входного напряжения усилителя;
uout - выходное напряжение усилителя;
fsf - номинальная функция преобразования усилителя;
К - истинное значение коэффициента усиления усилителя;
Ksf - номинальное значение коэффициента усиления;
u0 - смещение нулевого уровня выходного напряжения усилителя;
dK - относительное изменение коэффициента усиления относительно номинального значения;
ud, dd - составляющие смещения нулевого уровня выходного напряжения и относительного изменения коэффициента усиления, обусловленные отклонениями параметров элементов усилителя от их номинальных значений;
udp - наибольшее (по модулю) допускаемое значение составляющей ud;
ddp - наибольшее (по модулю) допускаемое значение составляющей dd;
D0 - основная погрешность усилителя, приведенная ко входу;
Dos - систематическая составляющая основной погрешности усилителя;
![]() - случайная составляющая основной погрешности
усилителя;
- случайная составляющая основной погрешности
усилителя;
![]() - автокорреляционная функция случайной
составляющей основной погрешности усилителя;
- автокорреляционная функция случайной
составляющей основной погрешности усилителя;
tcor - интервал времени между коррекциями дрейфа нулевого уровня выходного напряжения и изменений коэффициента усиления, периодически проводящимися в процессе эксплуатации усилителя;
x1 - температура окружающего воздуха;
x2 - напряжение питания усилителя;
x1ref, x2ref - нормальные значения температуры окружающего воздуха и напряжения питания усилителя, соответственно;
Dx1, Dx2 - разности между реальными (в момент измерения) и нормальными значениями температуры окружающего воздуха и напряжения питания, соответственно;
![]() - функция влияния температуры окружающего
воздуха и напряжения питания усилителя на систематическую составляющую
погрешности усилителя;
- функция влияния температуры окружающего
воздуха и напряжения питания усилителя на систематическую составляющую
погрешности усилителя;
![]() - функция влияния температуры окружающего
воздуха и напряжения питания усилителя на дисперсию случайной составляющей
погрешности усилителя;
- функция влияния температуры окружающего
воздуха и напряжения питания усилителя на дисперсию случайной составляющей
погрешности усилителя;
d1, d2, l1, l2, f1, f2, g1, g2 - постоянные коэффициенты функций влияния;
S(w) - спектральная плотность случайной составляющей основной погрешности усилителя;
![]() - номинальная функция влияния;
- номинальная функция влияния;
![]() - предел (по модулю) допускаемых отклонений
функции влияния от номинальной функции влияния;
- предел (по модулю) допускаемых отклонений
функции влияния от номинальной функции влияния;
![]() - номинальная автокорреляционная функция
случайной составляющей основной погрешности;
- номинальная автокорреляционная функция
случайной составляющей основной погрешности;
![]() - предел (по модулю) допускаемых отклонений
автокорреляционной функции от номинальной автокорреляционной функции;
- предел (по модулю) допускаемых отклонений
автокорреляционной функции от номинальной автокорреляционной функции;
Dс - дополнительная погрешность усилителя;
Dop - предел (по модулю) допускаемой основной погрешности;
Dosp - предел (по модулю) допускаемой систематической составляющей основной погрешности;
Dcp - предел (по модулю) допускаемой дополнительной погрешности.
СПИСОК ЛИТЕРАТУРЫ
1. Земельман М. А. - Измерительная техника, 1973, № 4.
2. Земельман М. А. - Измерительная техника, 1966, № 11.
3. Земельман М. А., Кнюпфер А. П., Кузнецов В. П. - Измерительная техника 1969, № 2.
5. Тихонов В. И. Статистическая радиотехника, М.: Советское Радио, 1966, с. 95.
6. Земельман М. А. - Измерительная техника, 1985, № 6.
СОДЕРЖАНИЕ
2.1. Характеристики погрешности си. 9
2.2. Характеристики дополнительной погрешности си (чувствительности к влияющим величинам). 15
2.3. Динамические характеристики. 20
2.4. Взаимодействие между объектом измерений и си. 33
2.5. Неинформативные параметры выходного сигнала. 34
3. Основы выбора комплексов нмх си. 34
5. Подход к выбору комплекса нмх и значений норм. 43
6. Установление критериев существенности составляющих погрешности си. 45
7. Переход от новых mx си, регламентированных в гост 8.009-84, к традиционным mx. 49
Приложение 1 справочное Условные обозначения. 51
Приложение 2 справочное Пример установления некоторых нмх измерительного усилителя и их использования для расчета характеристик погрешности усилителя в реальных условиях его применения. 52
| Расположен в: |
|---|
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/7817
На эту страницу сайта можно сделать ссылку:
На правах рекламы:
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|


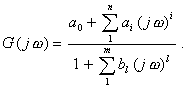
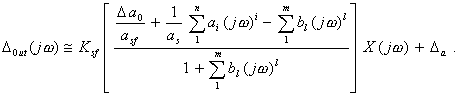
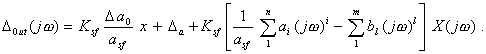
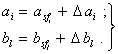
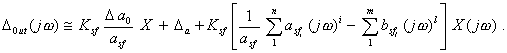
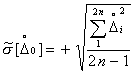 ;
;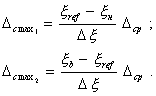
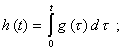
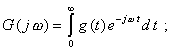
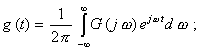
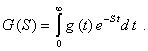
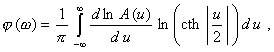
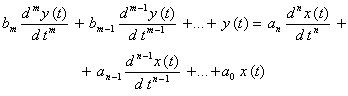
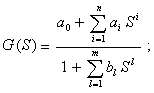
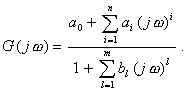
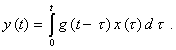
 ;
;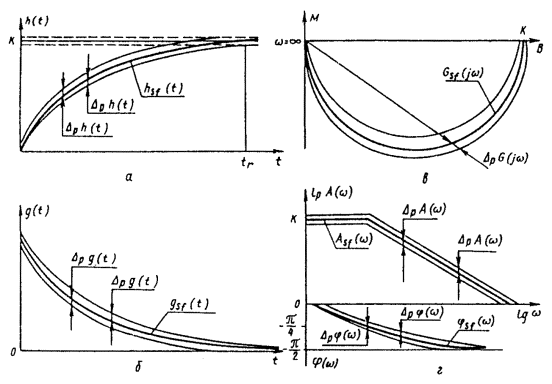
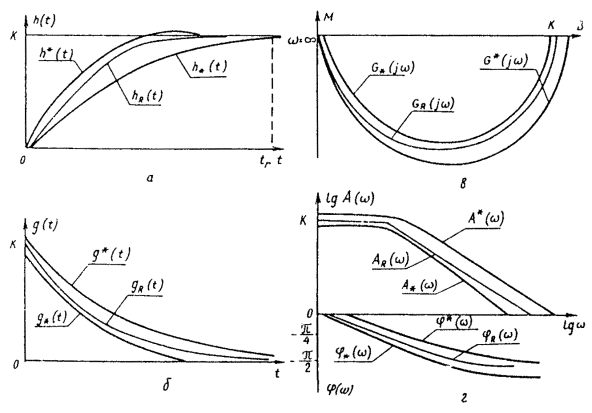
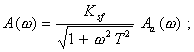
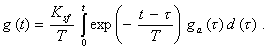
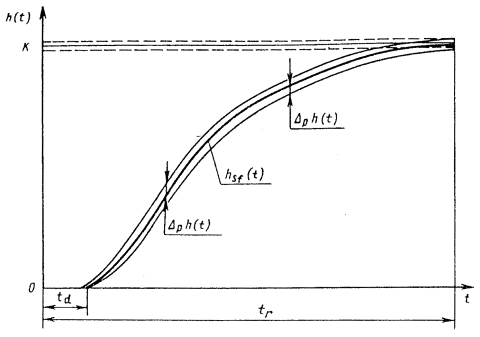
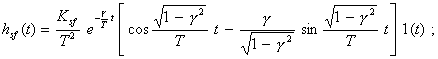
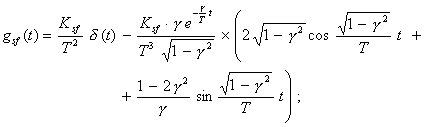
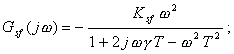
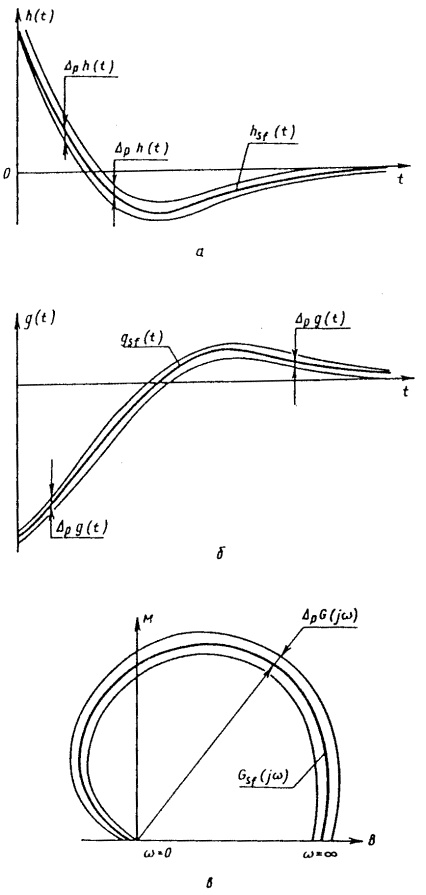
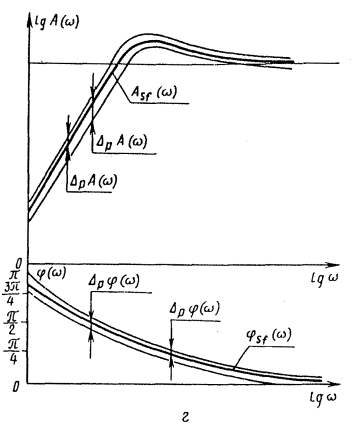
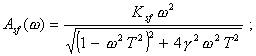
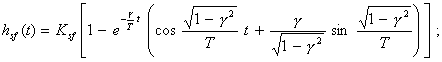
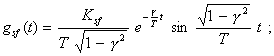
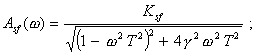
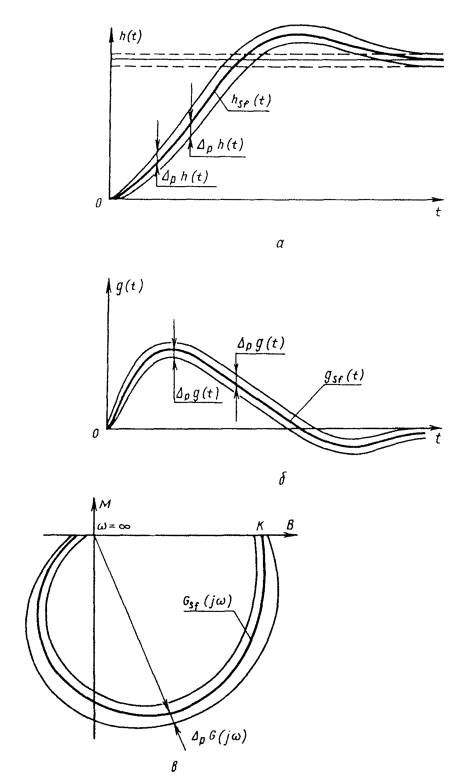
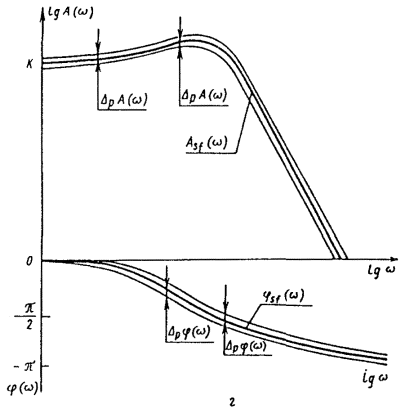
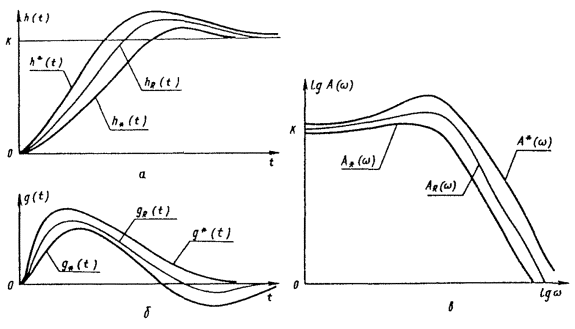
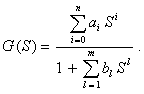
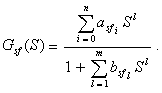
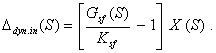
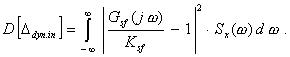
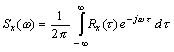 , где
, где 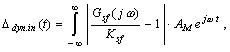
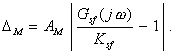
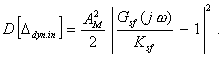
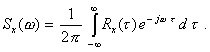
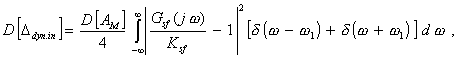
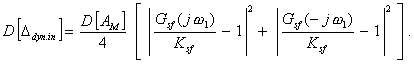
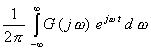 , а затем и переходную характеристику СИ - формула
, а затем и переходную характеристику СИ - формула 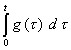 .
.