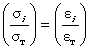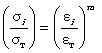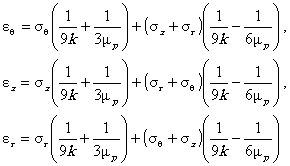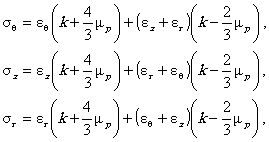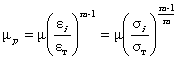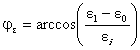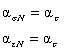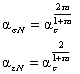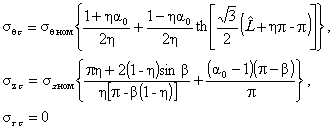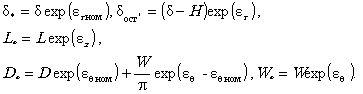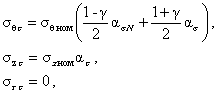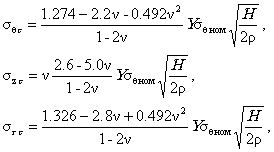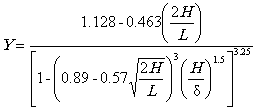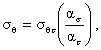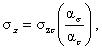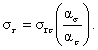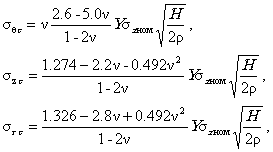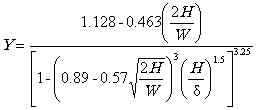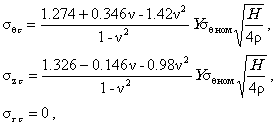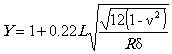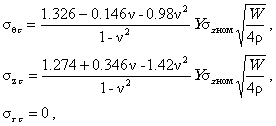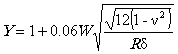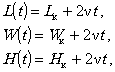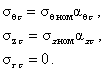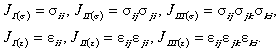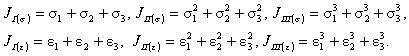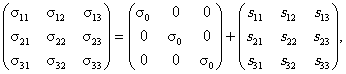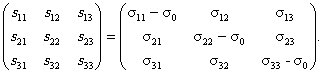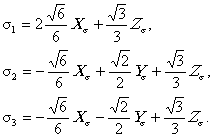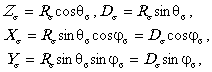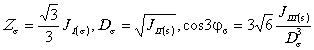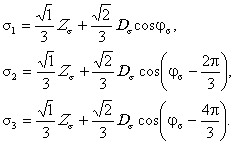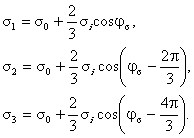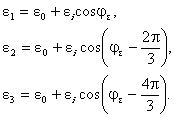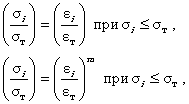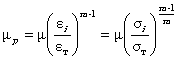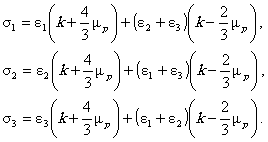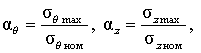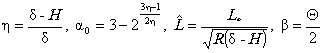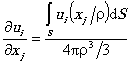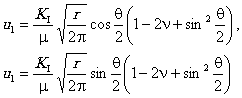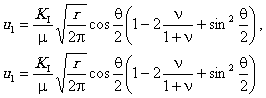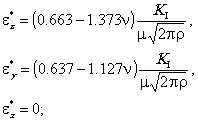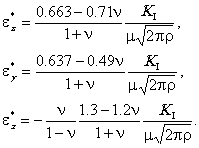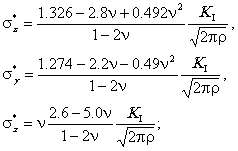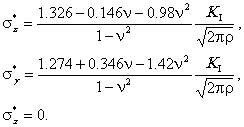
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"ВРД 39-1.10-004-99 Методические рекомендации по количественной оценке состояния магистральных газопроводов с коррозионными дефектами, их ранжирования по степени опасности и определению остаточного ресурса.
ОТКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО «ГАЗПРОМ» ВЕДОМСТВЕННЫЙ РУКОВОДЯЩИЙ ДОКУМЕНТ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО КОЛИЧЕСТВЕННОЙ ОЦЕНКЕ СОСТОЯНИЯ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ С КОРРОЗИОННЫМИ ДЕФЕКТАМИ, ИХ РАНЖИРОВАНИЯ ПО СТЕПЕНИ ОПАСНОСТИ И ОПРЕДЕЛЕНИЮ ОСТАТОЧНОГО РЕСУРСА ВРД 39-1.10-004-99 МОСКВА 2000
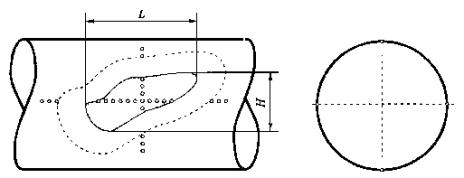
Система нормативных документов в газовой промышленности ВЕДОМСТВЕННЫЙ РУКОВОДЯЩИЙ ДОКУМЕНТ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО КОЛИЧЕСТВЕННОЙ ОЦЕНКЕ СОСТОЯНИЯ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ С КОРРОЗИОННЫМИ ДЕФЕКТАМИ, ИХ РАНЖИРОВАНИЯ ПО СТЕПЕНИ ОПАСНОСТИ И ОПРЕДЕЛЕНИЮ ОСТАТОЧНОГО РЕСУРСА ВРД 39-1.10-004-99 ОАО «ГАЗПРОМ» Производственное объединение Информационно-рекламный центр газовой промышленности Москва 2000 ПРЕДИСЛОВИЕ РАЗРАБОТАН Производственным объединением «Спецнефтегаз». ВНЕСЕН Управлением проектирования и экспертизы ОАО «Газпром». УТВЕРЖДЕН Членом Правления ОАО «Газпром» Б. В. Будзуляком 29 марта 1999г ВВЕДЕН В ДЕЙСТВИЕ Приказом ОАО «Газпром» от 15 февраля 2000 г. № 25 с 5 марта 2000 г сроком на три года. СОГЛАСОВАН Федеральным горным и промышленным надзором России от 16 ноября 1999 г. № 10-03/724, Управлением науки, новой техники и экологии, Управлением по транспортировке газа и газового конденсата ОАО «Газпром». ВВЕДЕН ВПЕРВЫЕ СОДЕРЖАНИЕ ВВЕДЕНИЕ «Методические рекомендации по количественной оценке состояния магистральных газопроводов с коррозионными дефектами, их ранжирования по степени опасности и определению остаточного ресурса» устанавливают правила и порядок проведения расчета степени опасности коррозионных повреждений труб магистральных трубопроводов в зависимости от размеров дефектов и действующих напряжений. Методические рекомендации предназначены для предприятий газовой промышленности и организаций, осуществляющих диагностический контроль и экспертизу технического состояния трубопроводов. Методические рекомендации разработаны в Управлении диагностики и ремонта ПО «Спецнефтегаз» (к. т. н. Мирошниченко Б. И., к. т. н. Аладинский В. В., к. т. н. Маханев В. О., к. т. н. Мельников В. Л.). ВРД 39-1.10-004-99 Система нормативных документов в газовой промышленности Ведомственный руководящий документ Методические рекомендации Дата введения 2000-03-05 1. ОБЩИЕ ПОЛОЖЕНИЯ1.1. Методика распространяется на линейные участки магистральных трубопроводов условным диаметром до 1400 мм включительно с избыточным давлением до 10 МПа, работающих в условиях статического нагружения и подверженных коррозионному воздействию внешней среды или транспортируемого продукта. 1.2. Методика содержит правила контрольного расчета и оценки остаточного ресурса участков трубопроводов с концентраторами напряжений в виде поверхностных коррозионных повреждений. 1.3. В методике принимается, что коррозионные дефекты могут как стабильно существовать, так и подрастать во времени. 1.4. Дефекты коррозионного происхождения подразделяются на следующие виды: 1.4.1. Общая коррозия - характеризуется квазиравномерной глубиной и значительной площадью поражения. 1.4.2. Язвенная коррозия - коррозия, локализованная на небольшой площади, но имеющая значительную глубину проникновения по толщине стенки труб. 1.4.3. Совмещение общей и язвенной коррозии - на фоне общей коррозии образование одной или множества «язвин» (наиболее распространенный тип коррозии). 1.4.4. Ручейковая коррозия - коррозия канавочного типа, образуется вдоль продольных и кольцевых швов, а также в местах расхождения стыков изоляционного покрытия труб. 1.5. Рассматриваются следующие состояния дефектов по степени их опасности (классы опасности): 1.5.1. Закритический дефект - дефект, при котором дальнейшая эксплуатация газопровода недопустима. 1.5.2. Критический дефект - дефект является допустимым только при создании до ремонта особых условий эксплуатации газопровода: снижение действующих нагрузок и ведение постоянного контроля за параметрами и состоянием дефекта методами наружной и внутритрубной дефектоскопии. 1.5.3. Докритический дефект - допустимый дефект при условии периодического контроля методами наружной и внутритрубной дефектоскопии. 1.5.4. Незначительный дефект - дефект, не оказывающий существенного влияния на надежность и долговечность эксплуатации газопровода; производится фиксация дефекта для последующих сравнений с результатами плановых обследований. 1.6. Основная цель методики - количественная оценка состояния дефектов и ранжирование их по степени опасности в соответствии с п. 1.5. 1.7. По результатам расчета данной методики производится принятие решений о следующих мероприятиях: - экстренная остановка эксплуатации газопровода; - проведение экстренного ремонта; - назначение срока ремонта; - снижение рабочего давления в газопроводе до заданной величины, определяемой расчетами, приведенными в методике; - назначение методов контроля за дефектом и его периодичности. 1.8. Методика не предназначена для проектных расчетов, так как она рассматривает те виды повреждений, которые не должны возникать при высококачественном ведении технологических процессов изготовления и контроля качества трубопроводов. 1.9. Уровни действующих нагрузок на участке газопровода с дефектами в каждом конкретном сечении труб определяются исходя из следующих приоритетов: - прямые измерения действующих напряжений в зоне дефекта (производится по специальной методике и средствами, приведенными в Приложении 1); - прямые измерения рабочего давления, произведенные внутритрубным снарядом-дефектоскопом, с последующим пересчетом напряженного состояния; - расчетные значения рабочего давления по длине газопровода по данным диспетчерских служб; - расчетные значения рабочего давления по длине газопровода в соответствии с нормативными документами [1]. 1.10. При проведении расчетов напряженно-деформированного состояния используются фактические данные о размерах трубы (диаметр и толщина стенки), размерах дефектов (длина, ширина, глубина), взаимном расположении дефектов и данные о механических свойствах, указанные в технических условиях на поставку труб, сертификационных документах или полученные экспериментально неразрушающими методами. 1.11. Коэффициенты запаса прочности, используемые в методике, назначаются как в соответствии с нормативными документами [1], так и на основании экспериментальных данных, полученных при натурных испытаниях труб и трубных секций. 1.12. Методика нормативно регламентируется для использования как временный документ, сроком на три года, по истечении которого будет произведено уточнение расчетных уравнений на основании статистической обработки накопленной базы данных. 1.13. Методика реализована в виде программного комплекса для ПК, рекомендованного к использованию при расчетах. 2. СХЕМАТИЗАЦИЯ НАГРУЗОК2.1. Расчеты по настоящей методике основываются на общепринятой схеме нагружения труб внутренним давлением (плоское напряженное и объемное деформированное состояние в стенке трубы). 2.2. В расчетах используются номинальные значения кольцевых sкц и продольных sпр напряжений. В цилиндрической системе координат, связанной с осью трубы, напряжения обозначаются sqном = sкц, szном = sпр. Радиальное напряжение srном принимается равным нулю. 2.3. Номинальные напряжения рассчитываются по значениям действующих на рассматриваемом участке трубопровода рабочего давления р, продольной силы Pпр, изгибающего момента Mпр:
где D и d - фактические значения внутреннего диаметра и толщины стенки трубопровода. 2.4. При известном значении давления р и неизвестных Pпр и Mпр кольцевое напряжение определяется по (2.1), а продольное принимается равным половине кольцевого: 2.5. Если величины давления р, продольной силы Pпр, изгибающего момента Mпр неизвестны, то кольцевое напряжение sкц задается по расчетному сопротивлению, которое определяется по [1] в зависимости от материала, условий работы, назначения трубопровода. В соответствии с [1] расчетное сопротивление R1 *) по условию прочности: *) В п. 2.5 используются обозначения, принятые в СНиП 2.05.06-85* [1]. Далее по тексту буквами т, R, k обозначены другие величины.
расчетное сопротивление R2 по условию деформативности:
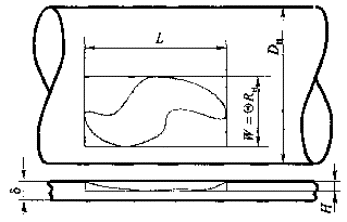
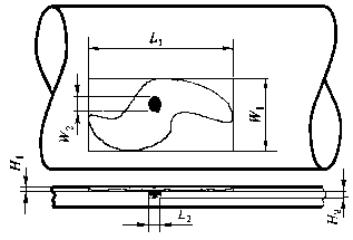
где 2.6. Для случая непосредственного измерения напряжений на участке трубопровода и в зоне дефекта в Приложении 1 приведена схема проведения измерений и последующего использования данных о напряжениях в расчетах. 3. СХЕМАТИЗАЦИЯ ДЕФЕКТОВ3.1. Исходными данными для схематизации дефектов являются результаты внутритрубной диагностики, непосредственных измерений или других неразрушающих способов контроля, получаемые по установленным методикам. 3.2. Поверхностный дефект в трубе с наружным диаметром Dн и толщиной стенки d представляется выемкой (рис. 3.1), глубиной Н, длиной L вдоль оси трубы и угловым размером Q в кольцевом направлении (ширина дефекта W равна QDн/2), под действием кольцевых (sqном, и продольных szном напряжений. Значения глубины Н, длины L, ширины W принимаются равными соответствующим наибольшим размерам дефекта. Рис. 3.1. Схематизация поверхностных дефектов 3.3. Дефект, представляющий собой явно выраженное одиночное глубокое повреждение («язва») на фоне общей коррозии - «совмещенный», заменяется двумя выемками (одна в другой) с размерами Н1, L1, W1 и H2,. L2, W2 (рис. 3.2). 3.3.1. Больший дефект с размерами Н1, L1, W1 рассматривается независимо. 3.3.2. Меньший дефект рассматривается как выемка с размерами H2,. L2, W2 в трубе с уменьшенной толщиной стенки d2:
и под действием увеличенных кольцевых sq1 и продольных sz1 напряжений (sq1 и sz1 - напряжения, вычисленные для дефекта 1 в соответствии с п. 4 с учетом возможного упруго-пластического деформирования). Рис. 3.2. Схематизация «совмещенных» дефектов 3.3.3. Данная схематизация
применяется, если размеры L2 и W2 - не превышают меньшее из
значений: 2d, 0.2L1, 0.2W1. В противном случае
проводится схематизация по п. 3.2 (глубина дефекта принимается равной
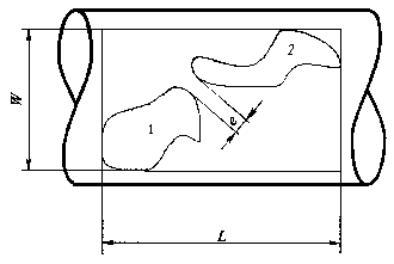
наибольшей глубине 3.3.4. Для нескольких близкорасположенных «язв» предварительно проводится анализ необходимости их объединения по п. 3.4. 3.4.1. Пусть в результате схематизации двух дефектов как одиночных (п. 3.2, п. 3.3.2) они имеют размеры L1, W1 и L2, W2. Расстояние eвл, на котором эти дефекты начнут влиять на напряженно-деформированные состояния друг друга равно
Если расстояние е между дефектами не превышает евл:
то дефекты объединяются и рассматриваются как
одиночный дефект с размерами H, L и W в
продольном и окружном направлениях (рис. 3.3). Глубина H
объединенного дефекта принимается равной наибольшей из Рис. 3.3. Схематизация близкорасположенных дефектов 3.4.2. Несколько близкорасположенных дефектов последовательно рассматриваются парами в соответствии с п. 3.4.1. 3.4.3. В процессе роста дефектов (п. 6) их размеры и взаимное расположение изменяются. В этом случае повторяется процедура проверки по п. 3.4.1 с объединением дефектов при необходимости. 3.5.
Узкие дефекты при 3.6.
Сквозные дефекты заменяются продольной трещиной длиной 4. РАСЧЕТ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ОБЛАСТИ ПОВРЕЖДЕНИЙ4.1. Анализ напряженно-деформированного состояния в зоне дефекта проводится с учетом возможного упруго-пластического деформирования. Для основных параметров напряженно-деформированного состояния используются следующие соотношения (Приложение 2). 4.1.1. Интенсивности напряжений и деформаций определяются по формулам: Связь между интенсивностями напряжений и деформаций принимается в виде степенной диаграммы деформирования: (4.2)
где sт - предел текучести, В соответствии с деформационной теорией пластичности [2] вводятся следующие уравнения, связывающие между собой компоненты деформаций и напряжений: или
где k - модуль объемного расширения, mp - упруго-пластический модуль сдвига: Упруго-пластический модуль сдвига mp в случае степенной диаграммы деформирования (4.2), равен mp = m при si £ sт (ei £ eт) (4.4б)
Помимо интенсивностей и компонентов деформаций и напряжений (4.1), (4.3) в расчетах используется объемная деформация e0: наибольшая деформация удлинения e1:
угол подобия девиатора деформаций je: 4.1.2. В области, содержащей
дефект, напряжения и деформации повышаются относительно номинальных.
Количественно это оценивается коэффициентами концентрации напряжений 4.1.3. Для локализованных
концентраторов (размеры дефектов сопоставимы с толщиной стенки трубы d), в то время как asи ae изменяются при
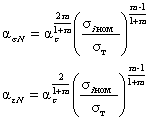
деформировании в упруго-пластической области, произведение asae по формуле Нейбера [3] остается постоянным и равным Используя (4.2) и (4.8), можно определить «Нейберовские» коэффициенты концентрации напряжений и деформаций во всем диапазоне нагрузок:
4.1.4. В общем случае коэффициенты концентрации напряжений и деформаций as, ae не равны asN, aeN , зависят от соотношений между размерами дефекта и трубы и соответствующим образом корректируются. 4.1.5. Для дефектов, имеющих в плане значительную площадь, в расчетах учитывается изменение размеров трубы и дефекта (увеличение диаметра, уменьшение толщины стенки), происходящее в процессе нагружения и ведущее к повышению фактически действующих в зоне дефекта напряжений. 4.2. Для поверхностных повреждений (рис. 3.1) расчет напряженно-деформированного состояния проводится по следующим уравнениям. 4.2.1. Условно-упругие компоненты напряжений рассчитываются в зависимости от размеров дефекта по формулам (Приложение 3): где
причем, размеры трубы и дефекта корректируются с учетом деформирования:
4.2.2. Интенсивность номинальных siном и местных упругих sie напряжений определяются в соответствии с (4.1), а упругий коэффициент концентрации ae: 4.2.3. По формулам (4.9) рассчитывается коэффициент концентрации asN. 4.2.4. Упруго-пластические компоненты напряжений в зоне дефекта равны: где 4.2.5. Компоненты деформаций eqном, ezном, erном и eq, ez, er, входящие в уравнения (4.10)-(4.12), связаны соотношениями (4.3) с соответствующими напряжениями sqном, szном, srном и sq, sz, sr. Таким образом, уравнения (4.10)-(4.12), с учетом (4.1)-(4.4) и (4.9), представляют собой систему нелинейных алгебраических уравнений относительно неизвестных напряжений sq, sz, sr и деформаций eq, ez, er, возникающих в зоне дефекта при приложении к трубе номинальных напряжений sqном, szном, srном. 4.2.6. Решение системы уравнений (4.10)-(4.12) осуществляется численными методами, реализованными в специализированном программном комплексе для ПК. 4.2.7. После определения напряженно-деформированного состояния в зоне дефекта по формулам (4.5)-(4.7) определяются другие параметры: объемная деформация e0, угол подобия девиатора деформаций je. 4.3. «Совмещенный» дефект (рис. 3.2). 4.3.1. Для большего дефекта (дефект 7) компоненты напряжений и деформаций определяются в соответствии с п. 4.2. 4.3.2. Для меньшего дефекта (дефект 2) расчет проводится по п. 4.2. с подстановкой в (4.10) вместо номинальных напряжений sqном и szном напряжений sq и sz, вычисленных в п. 4.3.1. При этом в соотношениях (4.10) размеры дефекта - L = L2, W= W2, H=H2, а толщина стенки принимается равной d - Н1 (рис. 3.2). 4.4. Продольная поверхностная трещина п. 3.5 4.4.1. Условно-упругие компоненты напряжений рассчитываются по формулам (Приложение 4):
где
r - характерный размер, отражающий чувствительность металла к концентрации напряжений [4, 5]; для современных трубных сталей r = 0.4-0.6 мм. 4.4.2. Интенсивности номинальных siном и местных упругих sie напряжений определяются по (4.1). 4.4.3. Упругий коэффициент концентрации ae определяется по формуле (4.11). 4.4.4. По формулам (4.9) определяется коэффициент концентрации напряжений as = aeN. 4.4.5. Упруго-пластические напряжения, действующие вблизи вершины трещины, равняются:
4.4.6. Используя (4.1)-(4.4), по полученным напряжениям вычисляются компоненты деформаций eq, ez, er, интенсивность деформаций ei. 4.4.7. По формулам (4.5)-(4.7) определяются объемная деформация e0 и угол подобия девиатора деформаций je. 4.5. Окружная поверхностная трещина (п. 3.5). 4.5.1. Условно-упругие компоненты напряжений рассчитываются по формулам (Приложение 4):
где
4.5.2. Далее расчет производится по пп. 4.4.2-4.4.7. 4.6. Продольная сквозная трещина (п. 3.6). 4.6.1. Условно-упругие компоненты напряжений рассчитываются по формулам (Приложение 4): где
4.6.2. Далее расчет производится по пп. 4.4.2-4.4.7. 4.7. Окружная сквозная трещина (п. 3.6). 4.7.1. Условно-упругие компоненты напряжений рассчитываются по формулам (Приложение 4): где
4.7.2. Далее расчет производится по пп. 4.4.2-4.4.7. 5. ПРЕДЕЛЬНЫЕ СОСТОЯНИЯ5.1. В данных методических рекомендациях расчет проводится по предельным состояниям, связанным с возникновением в наиболее нагруженной области дефекта такого уровня напряжений и деформаций, который приводит к нарушению сплошности металла. (Расчет по глобальным предельным состояниям, например, по условию потери устойчивости трубы должен осуществляться в соответствии с действующими нормативными документами). Применительно к наиболее нагруженной «точке» (на самом деле всегда подразумевается некоторый малый элемент металла, мысленно выделенный вокруг «точки») рассматриваются две основные категории предельных состояний: разрушение и исчерпание несущей способности (Приложение 5). В обоих случаях используются деформационные критерии предельных состояний и, соответственно, деформационные параметры (e0- объемная деформация, ei- интенсивность деформаций, e1 - наибольшая деформация удлинения, je- угол подобия девиатора деформаций) напряженно-деформированного состояния (п. 4.1). 5.1.1. Разрушение происходит при достижении предельной деформационной способности элемента металла: где e0f- - разрушающая объемная деформация, eif - разрушающая интенсивность деформаций. 5.1.2. Значительное формоизменение при упруго-пластическом деформировании может привести к уменьшению размеров и исчерпанию несущей способности элемента металла. Момент исчерпания несущей способности в значительной мере определяется степенью деформационного упрочнения металла. Предельная несущая способность достигается при условии (Приложение 5): где eiu - предельная равномерная деформация удлинения, первое слагаемое e0/e0u отражает влияние объемности деформированного состояния на уровень предельной равномерной деформации. Для степенной диаграммы деформирования eiu, примерно равна коэффициенту деформационного упрочнения т, коэффициент e0u равен - 0.5. 5.1.3. В качестве расчетного принимается то из предельных состояний (5.1), (5.2), которое наступает раньше. 5.1.4. Вычисление параметров e0, ei, je деформированного состояния, возникающего в области дефекта, осуществляется в соответствии с п. 4. 5.1.5. Критические деформации e0f, eif /и e0u, eiu, считаются характеристиками материала (Приложение 5). 5.2. Предельное состояние
одиночного дефекта (рис. 3.1) - течь в результате разрыва стенки (по
критериям 5.1.1 или 5.1.2) с образованием в зависимости от направления
наибольшей деформации удлинения продольного, длиной 5.3. В случае «совмещенного»
дефекта (рис.
3.3) анализ проводится раздельно для дефектов 1 и 2 по
п. 4.2
с учетом п.
3.3.2 для дефекта 2. Возможные предельные состояния: - для
дефекта 1 разрыв стенки (течь) с образованием сквозного дефекта, длиной 5.4. Предельное состояние несквозного трещиноподобного дефекта (п. 3.5) - течь в результате прорыва стенки с образованием продольного или окружного сквозного дефекта. Схематизация образовавшегося сквозного дефекта выполняется в соответствии с п. 3.6. 5.5. Предельное состояние сквозного трещиноподобного дефекта - страгивание трещины при достижении в вершине критического уровня деформаций (5.1) или (5.2), считающееся (в запас прочности) началом нестабильного протяженного разрушения участка трубопровода. 6. ПРОГНОЗИРОВАНИЕ РАЗВИТИЯ ДЕФЕКТА6.1. Коррозия приводит к росту повреждения в процессе эксплуатации. При этом концентрация напряжений и деформаций в области дефекта может интенсифицировать коррозионные процессы. Для оценки остаточного ресурса учитывается изменение размеров дефекта вплоть до предельных по п. 5. 6.2. Скорость роста дефекта в некоторой точке контура от коррозии под напряжением определяется по формуле [6]:
где n0 - скорость коррозии без напряжения, Сст и Сн - коэффициенты, характеризующие свойства стали и среды, ei - интенсивность деформаций, e0 - объемная деформация. 6.2.1. Для низкоуглеродистых и низколегированных сталей коэффициент Сст = 5-10. Коэффициент Сн допустимо вычислять по формуле [6]:
где k
- объемный
модуль упругости, V- мольный объем стали, 6.2.2. Деформации ei и e0 определяются в соответствии с п. 4. 6.3. В тех случаях, когда выполняется повторная дефектометрия для одного и того же поврежденного участка, скорость коррозии v вычисляется как
где DН - изменение размера дефекта за период времени Dt от одной до другой процедуры дефектометрии. 6.4. При недостаточном объеме информации о коррозионных свойствах металла и среды на данном участке трубопровода или об изменениях размеров дефекта во времени, скорость коррозии n принимается постоянной и равной 1 мм в год (выше наблюдаемых на практике скоростей коррозии, по крайней мере, на 40 %). 7. ПОРЯДОК ПРОВЕДЕНИЯ РАСЧЕТА7.1. Разделы 2-6 методики являются основой для проведения расчетов, однако порядок проведения конкретных расчетных работ существенно зависит как от цели расчета, так и от объема и достоверности имеющейся исходной информации. 7.2.1. По заданным размерам трубопровода (D, d) и механическим свойствам стали s02, sв (в данном расчете достаточно использовать типичные свойства трубных сталей, а не обязательно данные сертификата на поставку конкретной трубы) определяется проектное рабочее давление рраб (п. 2), соответствующее [I]. Схематизация дефекта проводится по п. 3.2. 7.2.2. Из системы уравнений (4.10)-(4.12) и условий (5.1), (5.2) определяются номинальные напряжения sqном, szном = sqном/2, далее определяется расчетное предельное давление ррасч: и расчетный коэффициент запаса по давлению np =ррасч/ pраб. 7.2.3. Если коэффициент запаса nр оказывается меньше допускаемого [np], то дефект считается закритическим (п. 1.5), необходимо снижение давления до безопасного уровня ррабnp /[np], решение вопроса о ремонте дефектного участка. 7.2.4. Выбор допускаемого коэффициента запаса [np] должен согласовываться с нормативными документами [1]. Для заданных размеров трубы введем давления р02 и рв, соответствующие возникновению в стенке трубы кольцевых напряжений, равных пределу текучести и прочности: Давление р02 - наибольшее допустимое по [1] давление при испытании линейных участков трубопроводов. Отношение давления рв к рабочему (нормативному) давлению рв / pраб(норм) представляет собой полный (проектный) коэффициент запаса в соответствии с [1]. Допускаемый коэффициент запаса [np] рекомендуется выбирать в диапазоне от р02 / pраб(норм) до рв / pраб(норм). В Приложении 6 приведены обобщенные номограммы допускаемых размеров дефектов с коэффициентами запаса [np] = р02 / pраб(норм) и [np] = рв / pраб(норм) и примеры их использования. 7.2.5. Если коэффициент запаса np превышает допустимый [np], то проводится расчет с учетом возможного развития дефекта. Принимается, что размеры дефекта изменяются во времени:
где Lк, Wк, Hк - размеры дефекта на момент контроля, v - постоянная скорость коррозии 1 мм/год (п. 6.4). Для системы уравнений (4.10)-(4.12), условий (5.1), (5.2), и соотношений (7.1), (7.2) находится значение tрасч такое, что выполняется
Расчетное время tрасч до образования предельно допустимого дефекта - остаточный ресурс (в условных годах) отражает степень опасности дефекта. Если время tрасч меньше 1 года, дефект считается критическим (п. 1.5). 7.2.6. Помимо остаточного ресурса tрасч при классификации дефектов по степени опасности учитываются возможные последствия разрыва стенки трубы в зоне дефекта. Считается, что после разрыва стенки образуется сквозной продольный или кольцевой дефект, который в зависимости от размеров может либо быть устойчивым, либо распространяться, приводя к разрушению участка трубопровода. Расчет таких дефектов проводится по п. 5.5 с применением уравнений (4.16) или (4.17) и схематизацией в соответствии с п. 3.6. Дефекты, для которых остаточный ресурс tрасч Д° разрыва стенки превышает 1 год, но существует опасность нестабильного распространения после разрыва стенки, считаются докритическими. Также докритическими считаются любые дефекты с ресурсом менее 5 лет. 7.2.7. Дефекты, для которых остаточный ресурс tрасч до разрыва стенки превышает 5 лет, и которые после разрыва стенки остаются в стабильном состоянии, считаются незначительными. 7.3. Определение уточненной оценки степени опасности вскрытого дефекта, его «живучести», уровня безопасного давления и т. д. проводится по п. 7.2 с использованием фактических параметров поврежденного участка. 7.3.1. Инструментальные измерения размеров и взаимного расположения вскрытых дефектов дают более высокую точность, чем внутритрубная диагностика. В частности, в этом случае возможно схематизация дефектов «совмещенными» (п. 3.3). 7.3.2. Механические свойства стали следует выбирать по данным сертификата на поставку труб или результатам неразрушающих испытаний. 7.3.3. Рабочее давление на участке трубопровода определяется прямыми измерениями внутритрубным снарядом или по данным диспетчерских служб. 7.3.4. По возможности, проводятся прямые измерения напряжений, действующих на поврежденном участке. 7.4. Общий порядок проведения работ по оценке опасности коррозионных дефектов описан в Приложении 7. Примеры расчетов представлены в Приложениях 8 и 9. ПРИЛОЖЕНИЕ 1. МЕТОДИКА ПРЯМЫХ ИЗМЕРЕНИЙ НАПРЯЖЕНИЙ, ДЕЙСТВУЮЩИХ В СТЕНКЕ ТРУБОПРОВОДАП1.1. Информация о величине действующих напряжений как на участке трубы, так и в зоне дефекта является основополагающей для количественной оценки работоспособности и ресурса участка газопровода с дефектами, поскольку позволяет ввести в расчеты фактические значения напряжений, действующие на конкретном дефекте, в конкретном месте участка трубопровода. Напряжения, действующие в трубопроводах, определяются совокупностью факторов таких, как внутреннее давление транспортируемого продукта, продольный изгиб трубопровода в вертикальной и горизонтальной плоскостях, поперечный изгиб стенки трубы (овальность, гофры, вмятины), температурные деформации, остаточные напряжения в зоне сварных швов, влияние концентраторов напряжений (несовершенства формы сварных стыков, технологические дефекты, повреждения, образовавшиеся в процессе эксплуатации). В зависимости от знака действующих от каждого фактора напряжений, они могут компенсироваться или суммироваться. В последнем случае возможно образование зон локального перенапряжения и протекание значительных пластических деформаций, (хотя давление транспортируемого продукта соответствует нормативному или ниже нормативного), что является основной причиной аварий на магистральных трубопроводах. П1.2. Средства измерений. П1.2.1. Значения действующих напряжений определяются с помощью ультразвукового измерителя напряжений «АСТ-2000». Измерения напряжений проводятся в соответствии с прилагаемой к прибору инструкцией по эксплуатации. П1.2.2. Прибор позволяет измерять как эквивалентные напряжения, так и в отдельности каждый из компонентов продольных и кольцевых напряжений в условиях плоского напряженного состояния. Значения действующих напряжений отражаются на экране дисплея в МПа. Погрешность измерений не превышает 5 % от предела текучести. П1.2.3. Прибор автоматически регистрирует толщину стенки трубы в зоне измерения с точностью ±0.01 мм, а также запас остаточной прочности в процентном отношении к пределу текучести стали трубы. П1.2.4. Все измеряемые параметры заносятся в память прибора, по окончании измерений возможна распечатка протокола. П1.3. Прямые измерения напряжений проводятся при обязательной шурфовке трубопровода, поскольку требуется контакт преобразователя измерителя с металлом трубы. Для этого производится снятие изоляции трубопровода в зоне измерений и зачистка с помощью шлифмашинки с автономным питанием. Площадь зачистки для каждого измерения составляет 50 ´ 50 мм2, диаметр контакта преобразователя прибора - 20 мм. Непосредственно перед измерением на рабочую поверхность преобразователя наносится акустоконтактная жидкость. П1.4. Место измерения в зависимости от вида дефекта определяется по следующей схеме (рис. П1.1):
Рис. П1.1. Точки измерения напряжений в зоне дефекта П1.4.1. Общая коррозия - в местах минимальной (по возможности) и максимальной остаточной толщины стенки трубы. П1.4.2. Язвенная коррозия - в околодефектной зоне. П1.4.3. Стресс-коррозия - в центре колонии и вблизи трещины наибольшей длины. П1.4.4. Линейные дефекты - в околодефектной зоне в середине длины дефекта. П1.4.5. Дефекты металлургического характера, в том числе расслоения - над центром площади дефекта. П1.4.6. Дефекты сварных соединений - по усилению сварного шва и околошовной зоне. П1.4.7. Дефекты геометрии сечения трубы - по центру площади деформации и далее по линии образующей трубы, проходящей через центр, с шагом 100 мм до конца деформированной зоны. Аналогично, от центра по линии периметра трубы. Независимо от шага, измерения проводятся в обязательном порядке в местах экстремального изгиба стенки в ортогональных направлениях относительно оси трубы. П1.4.8. Кроме непосредственно дефектных зон, проводится измерение напряжений, если имеется доступ, по бездефектному металлу трубы в 4-х диаметрально противоположенных точках по периметру трубы. П1.5. Обработка результатов и представление данных в программы расчета. П1.5.1. Определяются наибольшие значения действующих напряжений в зоне дефекта в кольцевом sqд и продольном szд направлениях. П1.5.2. Определяются напряжения, действующие в бездефектной зоне в кольцевом sqб и продольном szб направлениях, и соответствующее давление pизм=2sqбd ¤ D. П1.5.3. Определяются упругие коэффициенты концентрации напряжений в кольцевом aqe = sqб ¤ sqд и продольном aze = szб ¤ szд направлениях. П1.5.4. С учетом разницы между рабочим давлением рраб, при котором происходит эксплуатация трубопровода, и давлением ризм, при котором проводятся измерения, вычисляются кольцевые sqном = sqб(рраб ¤ ризм) и продольные szном = szб(рраб ¤ ризм)) номинальные напряжения. П1.5.5. Определяются условно-упругие компоненты напряжений в зоне дефекта (см. также п. 4.2.1):
П1.5.6. Далее проводится расчет по пп. 4.2.2-4.2.4 и 4.2.7. (В формуле (4.12б) можно использовать значения L, D, d, без учета их изменения при деформировании). ПРИЛОЖЕНИЕ 2. ПАРАМЕТРЫ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯП2.1. Напряженно-деформированное состояние в некоторой точке тела описывается симметричными второго ранга тензорами напряжений с компонентами sij и деформаций с компонентами еij. Для каждого симметричного тензора второго ранга можно выбрать оси координат таким образом, чтобы все составляющие с различающимися индексами i ¹ j обращались в нуль. Такие оси координат называются главными. В результате приведения тензора напряжений (деформаций) к главным осям ненулевыми остаются только диагональные компоненты s11, s22, s33 (e11, e22, e33) соответствующих тензоров. Обычно эти компоненты нумеруются в порядке убывания. s1 ³ s2 ³ s3 (e1 ³ e2 ³e3) Если около рассматриваемой точки тела выделить бесконечно малый прямоугольный параллелепипед с гранями, перпендикулярными главным осям тензора напряжений, то на него будут действовать только нормальные напряжения s1, s2, s3. Прямоугольный параллелепипед с гранями, перпендикулярными главным осям тензора деформаций, удлиняется (укорачивается) в направлениях главных осей в отношениях 1 + e1, 1 +e2, 1 +e3, но не искривляется, т. е. прямые углы остаются прямыми. Для тензоров sij, eij можно ввести систему инвариантов путем последовательной свертки тензорных произведений: Здесь и в дальнейшем подразумевается суммирование по повторяющимся индексам. В главных координатах инварианты (П2.1) выражаются через главные напряжения (деформации):
Наряду с инвариантами JI, JII, JIII или главными напряжениями (деформациями) могут быть введены и другие системы инвариантных величин, вполне определяющих соответствующий тензор и не зависящих от поворота осей координат. Инварианты одной системы могут быть выражены через инварианты другой. Тензор напряжений sij (равно как и любой симметричный тензор второго ранга) можно представить в виде суммы тензора гидростатического напряжения s0 и девиатора (отклонения от гидростатического состояния) sij: где
В главных осях гидростатические и девиаторные компоненты записываются в виде
Основными свойствами девиатора sij являются его независимость от гидростатической составляющей s0 и равенство нулю суммы диагональных компонент:
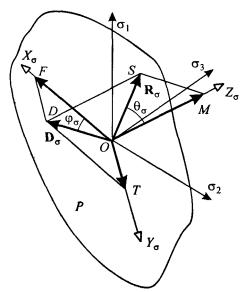
Рис. П2.1. Напряженное состояние в пространстве главных напряжений П2.2. Произвольному напряженному состоянию в пространстве главных напряжений соответствует точка S с координатами s1, s2, s3 (рис. П2.1) и вектор rs = OS. Проведем через начало координат ось Zs равнонаклоненную к каждой из осей s1, s2, s3 (гидростатическую ось) и плоскость Р перпендикулярную оси Zs - девиаторную плоскость. Введем в девиаторной плоскости Р оси Хs и Ys, причем ось Хs направим вдоль проекции оси s1 на девиаторную плоскость, а ось Ys перпендикулярно оси Хs так, чтобы Хs, Ys, Zs образовывали правую тройку. Вектор rs может быть представлен в виде суммы вектора ОМ, направленного вдоль гидростатической оси Zs, и вектора Ds = OD, лежащего в девиаторной плоскости Р. В свою очередь вектор Ds раскладывается на векторы OF и ОТ, направленные вдоль осей Хs и Ys соответственно. Проекции вектора Rs будут равны:
Проекции Ds, Хs, Ys, (П2.9)-(П2.11) содержат только компоненты девиатора, a Zs - только гидростатическую составляющую тензора напряжений. Главные напряжения выражаются через компоненты Хs, Ys, Zs в виде
Помимо системы Хs, Ys, Zs введем сферическую систему координат Rs, qs, js:
где Rs - длина вектора Rs, qs - угол между вектором Rs и гидростатической осью Zs, Ds - длина вектора Ds, js - угол между вектором Ds и осью Хs (угол подобия девиатора напряжений). Параметры Zs, Ds, js могут использоваться как система инвариантов тензора напряжений. Эти параметры определяются через инварианты JI, JII, JIII по следующим формулам:
Таким образом, Zs, Ds характеризуют уровень гидростатической и девиаторной составляющих тензора напряжений, а угол js - вид девиатора. Для главных напряжений запишем: Соотношения (П2.3)-(П2.16) полностью применимы и к тензору деформаций, и к любому другому симметричному тензору второго ранга. Во многих приложениях пользуются гидростатическим напряжением s0 (П2.4) и интенсивостью напряжений si, равной
В этом случае уравнения (П2.16) записываются, с учетом (П2.9), (П2.12), в виде
Интенсивность деформаций ei принято определять как
Здесь через е1, е2, е3 обозначены главные компоненты девиатора деформаций. Главные деформации будут равны:
П2.3. В нагруженном теле напряжения и деформации связаны друг с другом, причем в общем случае весьма сложным образом. При решении задач механики деформируемого твердого тела применяются различные теории, базирующиеся на тех или иных предположениях об уравнениях связи между напряжениями и деформациями (уравнениях состояния). Для металлических конструкций используются теория упругости, деформационная теория пластичности, теория течения. В дальнейшем мы будем ориентироваться на простейшие соотношения теорий упругости и упруго-пластических деформаций. Уравнения состояния сводятся к следующим:
где k - модуль объемного расширения. mp - упруго-пластический модуль сдвига:
определяемый по диаграмме деформирования si - ei. При напряжениях si меньших, чем предел текучести sт, т. е. при упругом деформировании, уравнение (1.22) записывается в виде
где m - упругий модуль сдвига. При si ³ sт связь между интенсивностью напряжений и интенсивностью деформаций для многих конструкционных материалов удовлетворительно описывается степенной функцией: где sт. - предел текучести, eт = sт ¤ 3m- интенсивность деформаций, соответствующая пределу текучести, m - коэффициент упрочнения. Для степенной диаграммы деформирования (П2.26) модуль сдвига mp равен: mp = m при si £ sт, (П2.27)
Используя уравнения (П2.21)-(П2.23) получаем соотношения, связывающие компоненты напряжений и деформаций:
Уравнения состояния могут быть существенно сложнее введенных формулами (П2.21)-(П2.23), однако общим остается функциональная (иногда в виде дифференциальных уравнений) связь между напряжениями и деформациями в нагруженном теле. ПРИЛОЖЕНИЕ 3. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ В ТРУБЕ С ПОВЕРХНОСТНЫМИ ДЕФЕКТАМИП3.1. Распределение напряжений и деформаций на участке трубы с поверхностным дефектом (рис. 3.1) оказывается весьма сложным и зависящим от многих параметров (диаметр трубы, толщина стенки, размеры дефекта, кольцевые и продольные номинальные напряжения). Аналитическое решение в общем случае получить невозможно, поэтому был проведен конечноэлементный анализ в широком диапазоне соотношений размеров труб и дефектов (d/R = 0.015... 0.030; L/R = 0.01... 3.0; Q = 1...3600; H/d = 10...90%) отдельно для кольцевых и продольных напряжений. Примеры такого анализа в виде уровней концентрации напряжений при d/R = 0.02; L/R = 1.4; Q = 24°; H/d = 50 % приведен на рис. П3.1 для кольцевых (рис. П3.1, а) и продольных напряжений (рис. П3.1, б). Рис. П3.1. Пример конечноэлементного решения о распределении напряжений в области дефекта в виде коэффициентов концентрации напряжений: а - кольцевых; б - продольных П3.2. Уровень нагруженности можно охарактеризовать коэффициентами концентрации кольцевых aq и продольных az напряжений, возникающих в дефектной зоне:
где sqmax и szном - наибольшие значения кольцевых и продольных напряжений соответственно. ПЗ.З. Зависимости коэффициентов концентрации кольцевых aq и продольных az напряжений от размеров дефектов приведены на рис. П3.2.
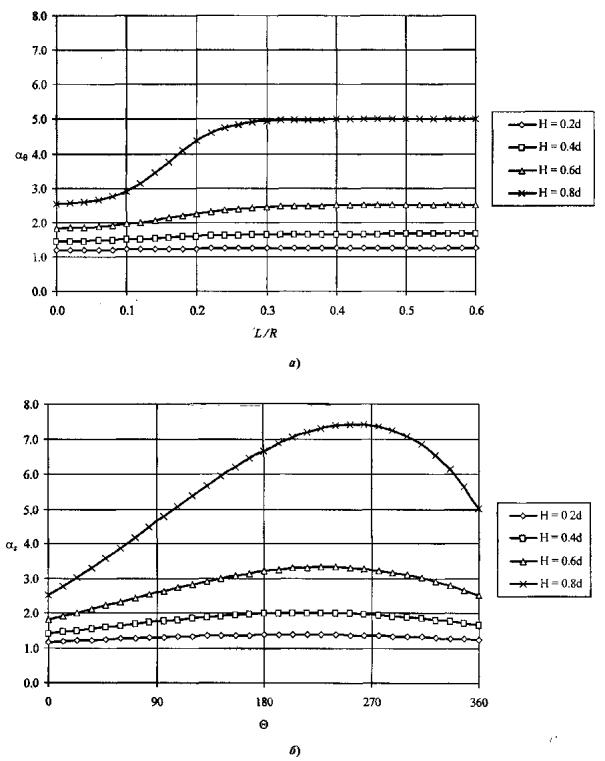
Рис. П3.2. Зависимости коэффициентов концентрации напряжений от размеров дефектов: а - кольцевые напряжения; б - продольные напряжения С достаточной точностью (погрешность не более 1 %) эти зависимости могут быть аппроксимированы формулами:
где
ПРИЛОЖЕНИЕ 4. ОПРЕДЕЛЕНИЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ У ВЕРШИНЫ ТРЕЩИНЫ МЕТОДОМ ЛОКАЛЬНЫХ ДЕФОРМАЦИЙП4.1. В методе локальных деформаций [4, 5] считается, что процессы деформирования, накопления повреждений, разрушения происходят в некотором небольшом, но конечном объеме металла (здесь существует аналогия с понятием «структурного элемента»). В качестве такого «элементарного объема» принят мысленно выделенный в металле шар радиуса r; r - характерный размер, отражающий чувствительность металла к концентрации напряжений. Считается, что напряженно-деформированное состояние шара контролируется перемещениями иi (i = 1,2, 3) его границы S. По значениям перемещений вычисляются осредненные по объему производные ¶ui ¤ ¶xj и деформации В общем случае определение перемещений иi и деформаций eij* требует применения численных методов, однако при рассмотрении области вблизи вершины трещины возможны некоторые упрощения. П4.2. Для трещины нормального отрыва перемещения вблизи вершины определяются по формулам [7] для случая плоской деформации или для плоского напряженного состояния. Здесь К1 - коэффициент интенсивности напряжений, m - модуль упругости при сдвиге, n - коэффициент Пуассона, r и q - полярные координаты рассматриваемой точки. Если центр шара расположен на продолжении трещины на расстоянии r, то при подстановке (П4.3) или (П4.4) в (П4.1) и (П4.2) получим для e* при плоской деформации:
при плоском напряженном состоянии:
По деформациям e* определяются соответствующие напряжения s* при плоской деформации при плоском напряженном состоянии: П4.3. Используемые в расчетах соотношения пп. 4.4-4.7 построены по формулам (П4.7), (П4.8) с учетом зависимости коэффициента интенсивности напряжений КI от формы и размеров трещины, размеров трубы, номинальных напряжений [7-9]. ПРИЛОЖЕНИЕ 5. КРИТЕРИИ ПРЕДЕЛЬНОГО СОСТОЯНИЯ МЕТАЛЛАП5.1. Выбор критериев предельных состояний материала состоит в построении некоторой функции от компонентов напряжений и деформаций и сопоставлении значений этой функции для действующего напряженно-деформированного состояния с критическими значениями, характеризующими свойства материала:
Когда определена связь между напряжениями и деформациями, для построения критерия достаточно только напряжений или только деформаций
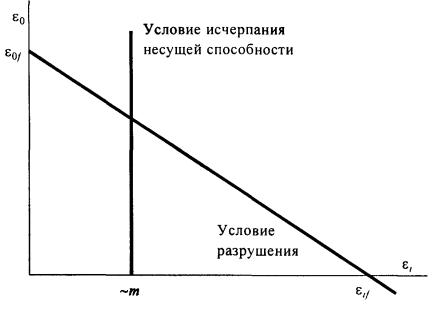
или Для пластичных металлов целесообразно использовать деформационные критерии (П5.1в). П5.2. При статическом нагружении разрушение металла связывают с исчерпанием его деформационной способности [3]. Основная доля деформирования приходится на пластические деформации, связанные с формоизменением (характеризуется интенсивностью пластических деформаций ei), однако уровень пластического деформирования, при котором происходит разрушение, весьма существенно зависит от объемности напряженно-деформированного состояния. Объемность напряженно-деформированного состояния можно оценивать различными параметрами [3], но наиболее естественным представляется объемная деформация e0. В таком случае, критерий разрушения можно представить в виде Анализ данных многочисленных экспериментов показывает, что с точностью, соответствующей точности определения механических свойств, связь между ei и e0 в (П5.2а) линейна, т. е. критерий (П5.2а) можно записать в виде уравнения прямой линии (рис.П5.1):
где e0f - разрушающая объемная деформация (при ei = 0), eif - разрушающая интенсивность деформаций (при e0 = 0). Рис. П5.1. Деформационные критерии предельных состояний металла П5.3. Значительное формоизменение при упруго-пластическом деформировании может привести к уменьшению размеров элемента металла и исчерпанию его несущей способности еще до разрушения (Типичный пример - образование «шейки» при одноосном растяжении). После того, как такое состояние достигнуто, дальнейшее деформирование происходит без увеличения нагрузки, неустойчиво. Очевидно, что, хотя металл еще некоторое время сохраняет свою целостность, момент исчерпания несущей способности, даже в ограниченном объеме металла, следует считать недопустимым предельным состоянием. П5.3.1. Рассмотрим элемент металла в виде кубика l0´l0´l0 под действием напряжений s1, s2, s3. В результате нагружения кубик превратится в параллелепипед с размерами l1´ l2´ l3. Усилие P1, передаваемое через элемент металла в направлении наибольшего напряжения s1, будет равно:
здесь учтено то, что по определению истинные деформации удлинения равны:
П5.3.2. Можно показать, что для степенной диаграммы деформирования (4.2) и в предположении «простого» нагружения усилие P1 достигает своего наибольшего значения при
или
где eiu = т, а e0u = -0.5. П5.4. При расчетах анализируется, какое из предельных состояний (П5.26) или (П5.46) наступает раньше, по нему и проводится расчет. П5.5. Ориентировочные значения механических свойств некоторых современных трубных сталей приведены в табл. П5.1. Табл. П5.1. Механические свойства трубных сталей
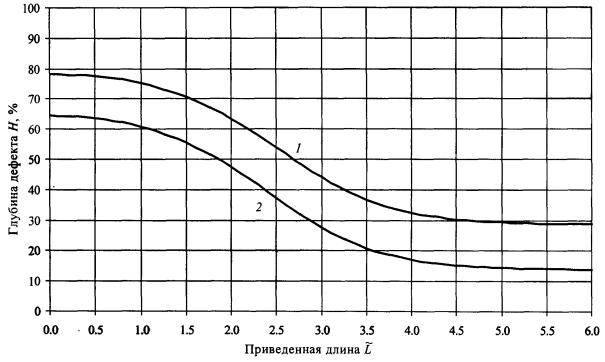
ПРИЛОЖЕНИЕ 6. НОМОГРАММЫ ДОПУСКАЕМЫХ РАЗМЕРОВ ДЕФЕКТОВП6.1. На рис. П6.1 - П6.8 приведены обобщенные
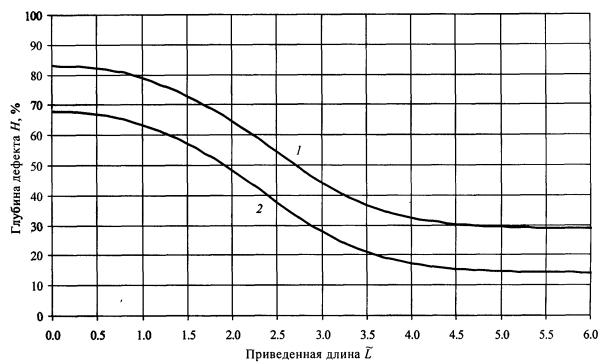
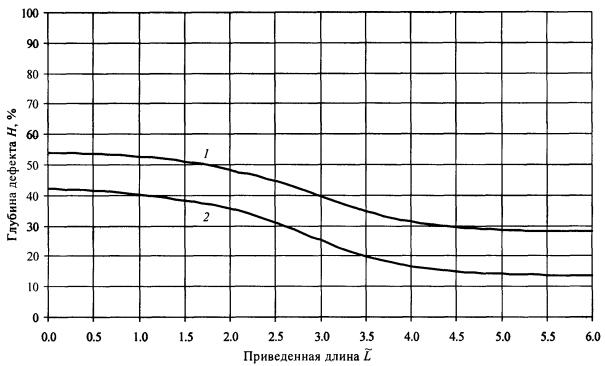
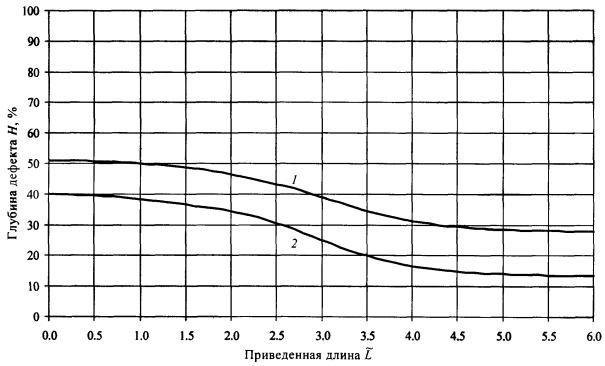
номограммы допускаемых размеров дефектов для двух уровней коэффициентов запаса
[пp] = p02 /.pраб(норм) (кривые 1) и [пp]
= pв /.pраб(норм) (кривые 2). Графики
разбиты на восемь групп в зависимости от ширины дефекта Q. По оси ординат откладывается приведенная
(безразмерная) длина дефекта по оси абсцисс - глубина дефекта в процентном отношении к толщине стенки. Рис. П6.1. Допускаемые размеры дефектов (ширина дефекта до 5°).
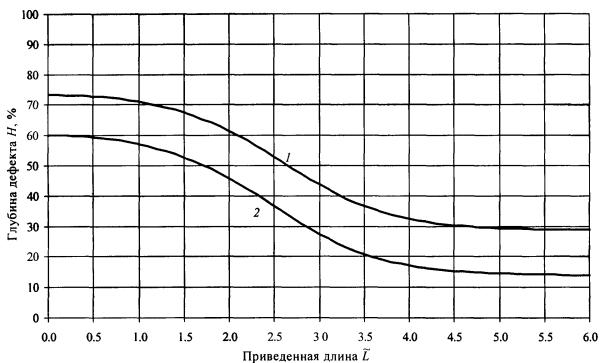
Рис. П6.2. Допускаемые размеры дефектов (ширина дефекта от 5 до 15°). Рис. П6.3. Допускаемые размеры дефектов (ширина дефекта от 15 до 30°).
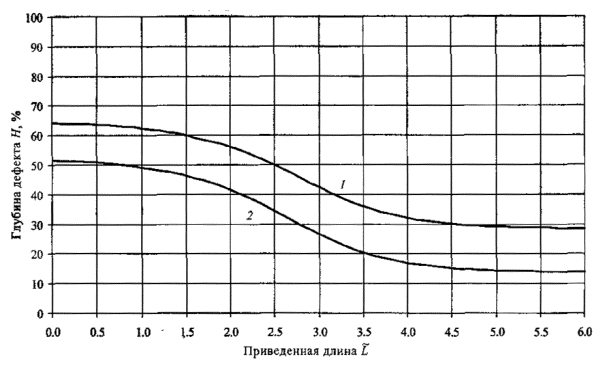
Рис. П6.4. Допускаемые размеры дефектов (ширина дефекта от 30 до 50°).
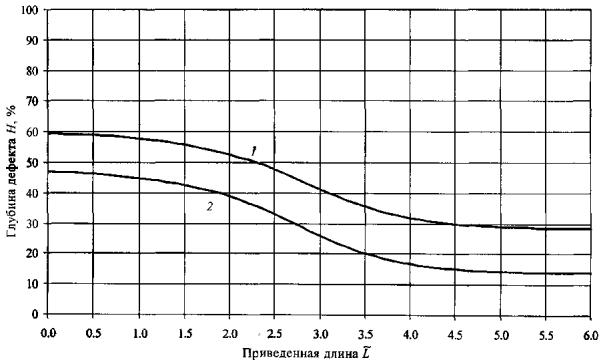
Рис. П6.5. Допускаемые размеры дефектов (ширина дефекта от 50 до 70°).
Рис. П6.6. Допускаемые размеры дефектов (ширина дефекта от 70 до 100°).
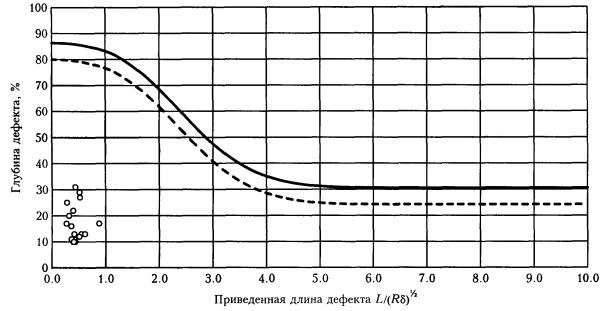
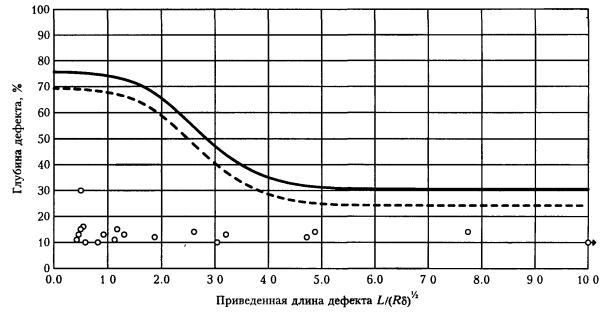
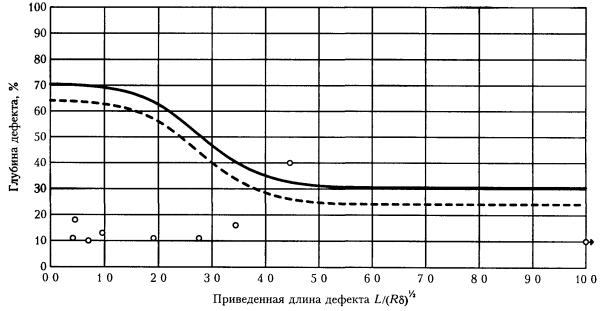
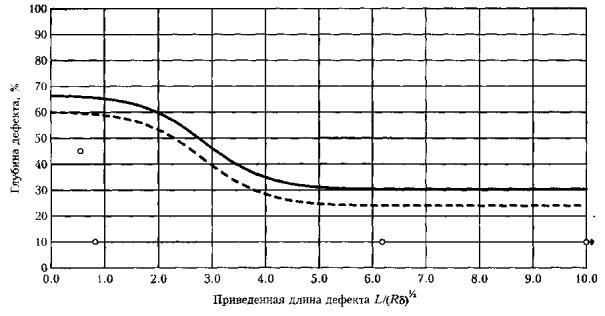
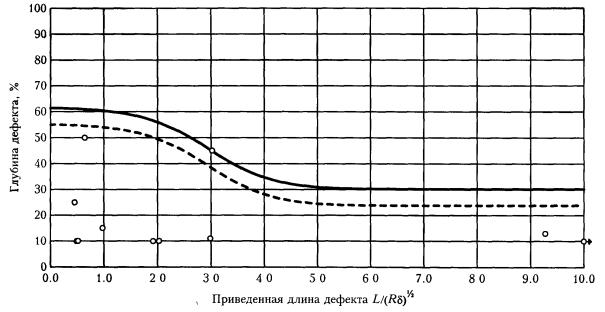
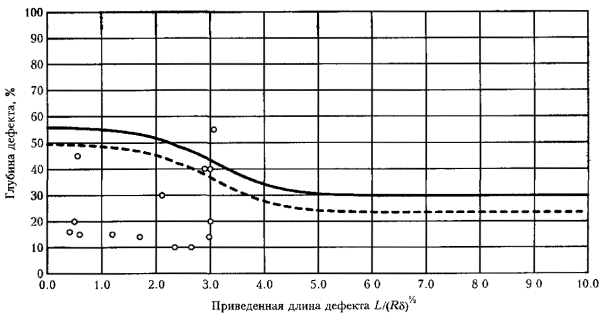
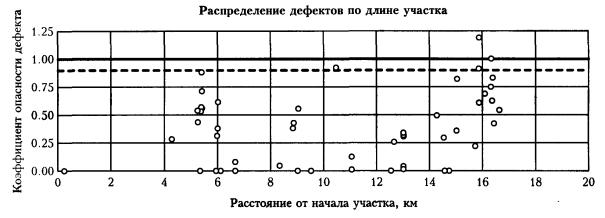
Рис. П6.7. Допускаемые размеры дефектов (ширина дефекта от 100 до 150°). Рис. П6.8. Допускаемые размеры дефектов (ширина дефекта свыше 150°). П6.2. Применение безразмерных координат и определение коэффициентов запаса на основе проектных позволяет использовать единые кривые для участков трубопроводов разных категорий, размеров, изготовленных из различных трубных сталей и спроектированных на различное рабочее давление. П6.3. Приведенные на рис. П6.1 - П6.8 номограммы могут использоваться для предварительной оценки работоспособности участков трубопроводов с коррозионными дефектами. Уточненный расчет проводится с помощью специализированной программы. ПРИЛОЖЕНИЕ 7. ПОРЯДОК ПРОВЕДЕНИЯ РАБОТ ПО ДВУХУРОВНЕВОЙ ОЦЕНКЕ ОПАСНОСТИ КОРРОЗИОННЫХ ДЕФЕКТОВП7.1. Настоящие методические рекомендации предназначены для расчета степени опасности коррозионных повреждений, выявленных как по результатам внутритрубной дефектоскопии (для всего массива дефектов), так и по отдельным дефектам. В связи с этим введена двухуровневая автоматизированная программная оценка степени опасности дефектов. П7.2. На первом уровне производится общая оценка опасности всех выявленных коррозионных дефектов и каверн на данном участке трубопровода с помощью специализированной программы расчета первого уровня и базы данных, представленной на компакт-диске (входит в комплект полного отчета по внутритрубной диагностике). Программой выполняется расчет и классификация дефектов по степени опасности. Выдается систематизированное представление данных об опасности коррозионных повреждений в зависимости от трехмерных размеров, информация о распределении дефектов и уровне их опасности по длине участка, а также рекомендации по снижению, при необходимости, рабочего давления в трубопроводе. - длина и ширина дефекта - штангенциркуль, рулетка с точностью ±5 мм; - глубина дефекта - толщиномер ультразвуковой с точностью ±0.1 мм; - расстояние между смежными дефектами (длина перемычки) - штангенциркуль, рулетка с точностью ±5 мм; - толщина стенки вне зоны дефекта - толщиномер ультразвуковой с точностью ±0.1 мм; - напряжения в зоне дефекта - измеритель напряжений АСТ-2000 с точностью ±5 % от предела текучести s02 (выполняется в соответствии с методикой, приведенной в Приложении 1); - механические свойства стали s02, sв - по данным сертификата на поставку труб. П7.4. Измеренные фактические данные состояния дефекта по П7.3 вносятся в расчетную программу второго уровня оценки опасности дефекта. П7.6. Данные по П7.5 оперативно представляются на ПК «Notebook». ПРИЛОЖЕНИЕ 8. ПРИМЕРЫ РАСЧЕТОВ ПО НОМОГРАММАМ ДОПУСКАЕМЫХ РАЗМЕРОВ ДЕФЕКТОВП8.1. По результатам внутритрубного обследования на участке трубопровода: диаметр - 1420 мм, рабочее (нормативное) давление - 7.4 МПа, толщина стенки - 15.7 мм выявлено коррозионное повреждение: длина - 320 мм, ширина - 280 мм, глубина - до 4 мм. П8.1.1. По формуле (П6.1) приведенная длина П8.1.2. По рис. П6.3. (ширина дефектов от 15 до 300) определяем, что рассматриваемый дефект лежит чуть ниже кривой 2, соответствующей проектной прочности трубы, т. е. расчетное предельное давление ррасч » pв. На момент обследования дефект можно считать неопасным П8.1.3. Марка стали рассматриваемой трубы - Х70 (s02 = 485 МПа, sв= 580 МПа). В таком случае, ррасч » pв = 12.8 МПа (pв определяется по формуле (7.2)), коэффициент запаса nрасч = 12.8 / 7.4 = 1.73. П8.1.4. При скорости коррозии 1 мм/год через 2.6 года рассматриваемый дефект достигнет глубины 6.6 мм (42 % от толщины стенки) и на графике (рис. П6.3) попадет на кривую 1 ррасч » p02 = 10.7 МПа, nрасч = 10.7 / 7.4 = 1.45). После этого момента дефект следует считать опасным (при проведении испытаний возможно разрушение по этому дефекту). П8.2. На участке газопровода диаметром 1020 мм (рабочее давление - 5.4 МПа) из стали 17Г1С (s02 =360 МПа, sв = 470 МПа) при толщине стенки 14 мм (категория В) обнаружены глубокие (до 50 %) одиночные «язвы» 20 ´ 20 мм. П8.2.1. По рис. П6.1. определяем, что прочность трубы с такими дефектами не ниже предусмотренной проектом. П8.2.2. При глубине 68 % (через 2.5 года при скорости коррозии 1 мм/год) прочность окажется ниже проектной. Опасными такие дефекты станут через 4.6 года при росте до глубины 83 %. П8.3. На участке газопровода диаметром 1020 мм (рабочее давление - 5.4 МПа) из стали 17Г1С (s02= 360 МПа, sв = 470 МПа) при толщине стенки 14 мм (категория В) дефектов не обнаружено. На площади 400 ´ 400 мм повреждена изоляция. П8.3.1. Приведенная длина - 4.73, ширина дефекта - 45°. П8.3.2. Анализ с помощью рис. П6.4 показывает, что при скорости коррозии на неизолированном участке 1 мм/год через 2 года (при глубине 14.7 %) прочность трубы окажется ниже проектной, а через 4 года (29 %) дефект станет опасным. ПРИЛОЖЕНИЕ 9. ПРИМЕР РАСЧЕТА КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ОПАСНОСТИ ДЕФЕКТОВ С ПОМОЩЬЮ СПЕЦИАЛИЗИРОВАННОЙ ПРОГРАММЫП9.1. Внутритрубное обследование выполнено производственным объединением «Спецнефтегаз» на одном из участков газопровода «Уренгой-Центр». Программа специально адаптирована к использованию базы данных о дефектности участка на компакт-диске, являющимся частью отчетной документации по проведенному обследованию. П9.2. Ниже приведены выдаваемые программой графики и таблицы с результатами расчетов и оценок. П9.2.1. Все дефекты, находящиеся в зоне графиков ниже сплошной кривой, не являются опасными. Пунктирная линия на графиках определяет зону опасности дефекта через 1 год эксплуатации. П9.2.2. На рис. П9.1 приведены зависимости степени опасности выявленных дефектов от линейных размеров дефектов - глубины, длины и ширины (по ширине данные сгруппированы дискретно по мере возрастания значений). П9.2.3. На рис. П9.2 приведены графики распределения дефектов с коэффициентами опасности по длине отдельных участков газопровода (по 20 км). П9.2.4. В таблице на рис. П9.3 приведены по каждому дефекту категория опасности, ресурс работы и рекомендуемые значения по снижению рабочего давления в газопроводе до безопасного уровня. Предельные размеры дефектов (ширина дефектов 10-60 мм) Предельные размеры дефектов (ширина дефектов 60-180 мм)
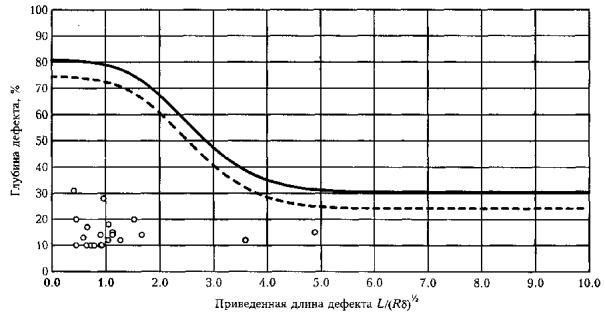
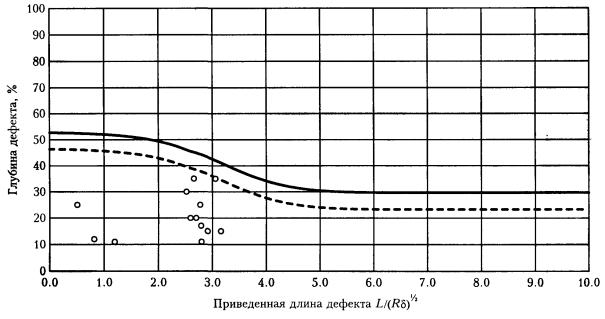
Рис. П9.1. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Зависимости степени опасности выявленных дефектов от их линейных размеров (начало) Предельные размеры дефектов (ширина дефектов 180-360 мм)
Предельные размеры дефектов (ширина дефектов 360-600 мм)
Рис. П9.1. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Зависимости степени опасности выявленных дефектов от их линейных размеров (продолжение) Предельные размеры дефектов (ширина дефектов 600-840 мм)
Предельные размеры дефектов (ширина дефектов 840-1200 мм)
Рис. П9.1. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Зависимости степени опасности выявленных дефектов от их линейных размеров (продолжение) Предельные размеры дефектов (ширина дефектов 1200-1800 мм)
Предельные размеры дефектов (ширина дефектов более 1800 мм)
Рис. П9.1. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Зависимости степени опасности выявленных дефектов от их линейных размеров (окончание)
Рис. П9.2. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Распределение дефектов с коэффициентами степени опасности по длине участка (начало)
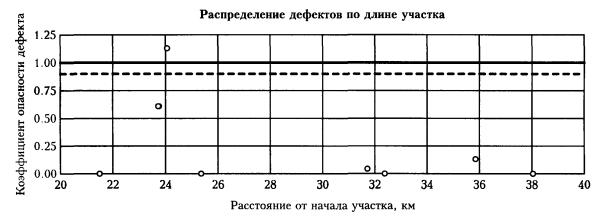
Рис. П9.2. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Распределение дефектов с коэффициентами степени опасности по длине участка (окончание)
Рис. П9.3. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Таблица выявленных дефектов с оценкой категории опасности, ресурса работы и рекомендуемым снижением рабочего давления в газопроводе до безопасного уровня (начало)
Рис. П9.3. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Таблица выявленных дефектов с оценкой категории опасности, ресурса работы и рекомендуемым снижением рабочего давления в газопроводе до безопасного уровня (продолжение)
Рис. П9.3. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Таблица выявленных дефектов с оценкой категории опасности, ресурса работы и рекомендуемым снижением рабочего давления в газопроводе до безопасного уровня (продолжение)
Рис. П9.3. Пример компьютерного анализа результатов внутритрубной дефектоскопии. Таблица выявленных дефектов с оценкой категории опасности, ресурса работы и рекомендуемым снижением рабочего давления в газопроводе до безопасного уровня (окончание) Литература1. СНиП 2.05.06-85*. Магистральные трубопроводы / Госстрой России. - М.: ГУП ЦПП, 1998. - 52 с. 2. Качанов Л. М. Основы теории пластичности. - М.: Наука, 1969. - 420 с. 6. Методические рекомендации. Механика катастроф. Определение остаточного ресурса элементов конструкций. М., 1996. - 160 с. 7. Партон В. 3., Морозов Е. М. Механика упруго-пластического разрушения. - М.: Наука, 1985.-504с. 8. МР 125-02-95. Правила составления расчетных схем и определения параметров нагруженности элементов конструкций с выявленными дефектами. М., НПО ЦНИИТМАШ, НИКИЭТ, 1995. - 52 с. ОСНОВНЫЕ ОБОЗНАЧЕНИЯD, R, Dн, Rн, d - внутренние и наружные диаметр и радиус, толщина стенки трубопровода; L, W,Q, H - длина, ширина линейная, ширина угловая, глубина дефекта; р, Pпр, Mпр - рабочее давление, продольная сила, изгибающий момент на участке трубопровода; s - напряжения: sкц - кольцевые, sпр - продольные, sq, sz, sr - компоненты в цилиндрических координатах, s0 - гидростатическое, si - интенсивность; e - деформации: eq, ez, er - компоненты в цилиндрических координатах, e0 - объемная, ei - интенсивность; a, as, ae- коэффициенты концентрации напряжений и деформаций; Е - модуль упругости; k - объемный модуль упругости; m - модуль сдвига (упругий); mp - модуль сдвига (упруго-пластический); n - коэффициент Пуассона; sт - предел текучести; s02- условный предел текучести; sв - предел прочности; т - коэффициент деформационного упрочнения; eif - разрушающая интенсивность деформаций; e0f - разрушающая объемная деформация; eiu - предельная равномерная деформация; e0u - предельная объемная деформация; r - характерный размер, отражающий чувствительность металла к концентрации напряжений; n - скорость коррозии под напряжением; n0 - скорость коррозии без напряжения.
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/8355
На эту страницу сайта можно сделать ссылку:
На правах рекламы: |
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|