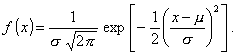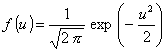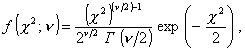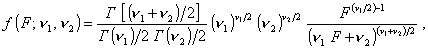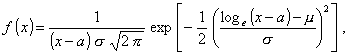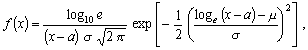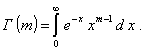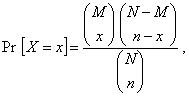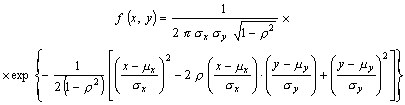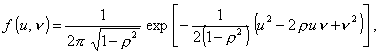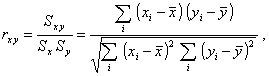ГОСТ Р 50779.10-2000
(ИСО 3534.1-93)
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ВЕРОЯТНОСТЬ И ОСНОВЫ СТАТИСТИКИ
Термины и определения
ГОССТАНДАРТ РОССИИ
Москва
ПРЕДИСЛОВИЕ
1. РАЗРАБОТАН И ВНЕСЕН Техническим комитетом по
стандартизации ТК 125 «Статистические методы в управлении качеством продукции»,
Акционерным обществом «Научно-исследовательский
центр контроля и диагностики технических систем» (АО «НИЦ КД»).
2. ПРИНЯТ И ВВЕДЕН В
ДЕЙСТВИЕ Постановлением Госстандарта России от 29 декабря 2000 г. № 429-ст.
3. Разделы настоящего
стандарта, за исключением разделов 1a, 1b и приложения А, представляют
собой аутентичный текст международного стандарта ИСО 3534.1-93 «Статистика.
Словарь и условные обозначения. Часть 1. Вероятность и основные статистические
термины».
4. ВВЕДЕН ВПЕРВЫЕ.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Установленные в стандарте термины расположены в
систематизированном порядке и отражают систему понятий в области теории
вероятностей и математической статистики.
Для каждого понятия установлен один
стандартизованный термин.
Недопустимые к применению термины-синонимы
приведены в круглых скобках после стандартизованного термина и обозначены
пометой «Ндп.».
Термины-синонимы без пометы «Ндп.» приведены в
качестве справочных данных и не являются стандартизованными.
Заключенная в круглые скобки часть термина может
быть опущена при использовании термина в документах по стандартизации.
Наличие квадратных скобок в терминологической
статье означает, что в нее включены два термина, имеющих общие терминоэлементы.
В алфавитных указателях данные термины приведены
отдельно с указанием номера статьи.
Приведенные определения можно при необходимости
изменить, вводя в них производные признаки, раскрывая значения используемых в
них терминов, указывая объекты, входящие в объем определяемого понятия.
Изменения не должны нарушать объем и содержание понятий, определенных в данном
стандарте.
Стандартизованные термины набраны полужирным
шрифтом, их краткие формы, представленные аббревиатурой, - светлым, а синонимы
- курсивом.
В стандарте приведены иноязычные эквиваленты
стандартизованных терминов на английском (en) и французском (fr) языках.
В настоящем стандарте
многие термины определены одновременно в разделе 1 и в разделе 2 в зависимости от того,
имеют ли они применение:
- теоретическое - в вероятностном смысле;
- практическое - в статистическом смысле.
Термины, определенные в разделе 1, сформулированы на
языке свойств генеральных совокупностей. В разделе 2 определения отнесены к
множеству наблюдений. Многие из них основаны на выборочных наблюдениях из
некоторой совокупности. Для того чтобы различать параметры генеральной
совокупности и результаты вычислений оценок параметров по выборочным данным, к
определениям ряда терминов из раздела 2 добавлено слово «выборочный» или
«эмпирический».
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ВЕРОЯТНОСТЬ И ОСНОВЫ СТАТИСТИКИ
Термины и определения
Statistical
methods. Probability and general statistical terms.
Terms and definitions
Дата введения 2001-07-01
Настоящий стандарт устанавливает термины и
определения понятий в области теории вероятностей и математической статистики.
Термины, установленные настоящим стандартом,
обязательны для применения во всех видах документации и литературы по
статистическим методам, входящих в сферу работ по стандартизации и (или)
использующих результаты этих работ.
В настоящем стандарте использованы ссылки на
следующие стандарты:
ГОСТ Р 50779,11-2000 (ИСО 3534.2-93)
Статистические методы. Статистическое управление качеством. Термины и
определения.
ИСО 31.0-921) Величины и единицы
измерения. Часть 0. Общие принципы.
ИСО 31.1-921) Величины и единицы
измерения. Часть 1. Пространство и время.
ИСО 31.2-921) Величины и единицы
измерения. Часть 2. Периодические явления.
ИСО 31.3-921) Величины и единицы
измерения. Часть 3. Механика.
ИСО 31.4-921) Величины и единицы
измерения. Часть 4. Термообработка.
ИСО 31.5-921) Величины и единицы
измерения. Часть 5. Электричество и магнитное излучение.
ИСО 31.6-921) Величины и единицы
измерения. Часть 6. Световое и электромагнитное излучение.
ИСО 31.7-921) Величины и единицы
измерения. Часть 7. Акустика.
ИСО 31.8-921) Величины и единицы
измерения. Часть 8. Физическая химия и молекулярная физика.
ИСО 31.9-921) Величины и единицы
измерения. Часть 9. Атомная и ядерная физика.
ИСО 31.10-921) Величины и единицы
измерения. Часть 10. Ядерные реакции и ионовое излучение.
ИСО 31.11-921) Величины и единицы
измерения. Часть 11. Математические знаки и символы, используемые в физических
науках.
ИСО 31.12-921) Величины и единицы
измерения. Часть 12. Число характеристик.
ИСО 31.13-921) Величины и единицы
измерения. Часть 13. Физика твердого тела.
ИСО 3534.3-851) Статистика. Словарь и
условные обозначения. Часть 3. Планирование экспериментов.
ИСО 5725.1-911) Точность методов и
результатов измерений. Часть 1. Общие принципы и определения
1)
Оригиналы международных стандартов ИСО - во ВНИИКИ Госстандарта России.
|
1.1 вероятность
Действительное число в
интервале от 0 до 1, относящееся к случайному событию.
Примечания
1. Число может отражать
относительную частоту в серии наблюдений или степень уверенности в том, что
некоторое событие произойдет. Для высокой степени уверенности вероятность
близка к единице.
2. Вероятность события А обозначают Рr (А) или Р (А)
|
en probability
fr probabilite
|
|
1.2. случайная
величина
Переменная, которая
может принимать любое значение из заданного множества значений и с которой
связано распределение вероятностей.
Примечание - Случайную
величину, которая может принимать только отдельные значения, называют
дискретной. Случайную величину, которая может принимать любые значения из
конечного или бесконечного интервала, называют непрерывной.
|
en random variable; variate
fr variable aleatoire
|
|
1.3. распределение
(вероятностей)
Функция, определяющая
вероятность того, что случайная величина примет какое-либо заданное значение
или будет принадлежать заданному множеству значений.
Примечание - Вероятность
того, что случайная величина находится в области ее изменения, равна единице
|
en probability
distribution
fr loi de probabilite
|
|
1.4. функция
распределения
Функция, задающая для
любого значения х вероятность того, что случайная величина Х
меньше или равна х,
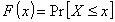
|
en distribution function
fr fonction de repartition
|
|
1.5. плотность
распределения (вероятностей)
Первая производная,
если она существует, функции распределения непрерывной случайной величины
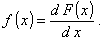
Примечание - 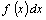 называется
элементом вероятности называется
элементом вероятности
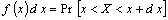
|
en probability
density function
fr fonction de densite de
probabilit
|
|
1.6. функция
распределения (вероятностей) масс
Функция, дающая для
каждого значения xi дискретной случайной величины Х вероятность pi того, что случайная величина
равна хi:
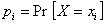
|
en probability
mass function
fr fonction de masse
|
|
1.7. двумерная функция распределения
Функция, дающая для любой пары значений х,
у вероятность того, что случайная величина X будет
меньше или равна х, а случайная величина Y - меньше
или равна y:
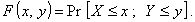
Примечание - Выражение в квадратных скобках означает
пересечение событий Х £ х и Y £ у
|
en bivariate distribution function
fr fonction de repartition a deux variables
|
|
1.8. многомерная функция распределения
Функция, дающая для любого набора значений х,
у, ... вероятность того, что несколько случайных величин X, Y,
... будут меньше или равны соответствующим значениям х, у, ...:
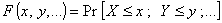
|
en multivariate distribution function
fr fonction de repartition a plusieurs variables
|
|
1.9. маргинальное распределение
(вероятностей)
Распределение вероятностей подмножества k1
из множества k случайных величин, при этом остальные (k - k1) случайные величины принимают
любые значения в соответствующих множествах возможных значений.
Примечание - Для распределения вероятностей трех случайных
величин X, Y, Z существуют:
- три
двумерных маргинальных распределения, т.е. распределения пар (X, Y),
(X, Z), (Y, Z);
- три одномерных маргинальных распределения, т.е.
распределения X, Y и Z.
|
en marginal probability distribution
fr loi de probabilite marginale
|
|
1.10. условное распределение (вероятностей)
Распределение подмножества k1 < k случайных величин
из распределения случайных величин, когда остальные (k - k1)
случайные величины принимают постоянные значения.
Примечание - Для распределения вероятностей двух случайных
величин X, Y существуют:
- условные распределения X: некоторое
конкретное распределение представляют как «распределение X при Y = y»; -
условные распределения Y: некоторое конкретное распределение представляют
как «распределение Y при Х = х».
|
en conditional probability distribution
fr loi de probabilite conditionnelle
|
|
1.11. независимость (случайных величин)
Две случайные величины Х и Y независимы, если их функции распределения
представлены как
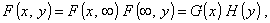
где F (х, ¥) = G
(х) и F (¥, у) = Н
(у) - маргинальные функции распределения X и Y, соответственно, для всех пар (х, у).
Примечания:
1. Для
непрерывной независимой случайной величины ее плотность распределения, если
она существует, выражают как
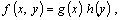
где g
(x) и h (у) - маргинальные плотности распределения Х
и Y, соответственно, для всех пар (х, у).
Для
дискретной независимой случайной величины ее вероятности выражают как
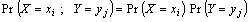
для
всех пар (xi, уj).
2. Два события независимы, если вероятность того,
что они оба произойдут, равна произведению вероятностей этих двух событий.
|
en independence
fr independance
|
|
1.12. параметр
Величина, используемая в описании распределения
вероятностей некоторой случайной величины.
|
en parameter
fr parametre
|
|
1.13. корреляция
Взаимозависимость двух или нескольких случайных
величин в распределении двух или нескольких случайных величин.
Примечание - Большинство статистических мер корреляции
измеряют только степень линейной зависимости.
|
en correlation
fr correlation
|
|
1.14. квантиль (случайной величины)
Значение случайной величины хp, для которого функция распределения принимает
значение p (0 £ p £ 1) или ее
значение изменяется скачком от меньшего p до
превышающего р.
Примечания
1.
Если значение функции распределения равно p во
всем интервале между двумя последовательными значениями случайной величины,
то любое значение в этом интервале можно рассматривать как p-квантиль.
2.
Величина хp будет p-квантилем,
если
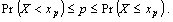
3. Для
непрерывной величины p-квантиль - это то значение переменной, ниже
которого лежит р-я доля распределения.
4. Процентиль - это квантиль, выраженный в
процентах.
|
en quantile
fr quantile
|
|
1.15. медиана
Квантиль порядка p = 0,5.
|
en median
fr mediane
|
|
1.16. квартиль
Квантиль порядка p = 0,25 или
p = 0,75.
|
en quartile
fr quartile
|
|
1.17. мода
Значение случайной величины, при котором функция
распределения вероятностей масс или плотность распределения вероятностей
имеет максимум.
Примечание - Если имеется единственная мода, то
распределение вероятностей случайной величины называется унимодальным; если
имеется более чем одна мода, оно называется многомодальным, в случае двух мод
- бимодальным.
|
en mode
fr mode
|
|
1.18. математическое ожидание (случайной
величины)
а) Для дискретной случайной величины X,
принимающей значения xi с вероятностями
pi,
математическое ожидание, если оно существует, определяют формулой
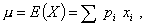
где суммируют все значения xi, которые может принимать случайная величина X.
b) Для непрерывной случайной величины X,
имеющей плотность f (x), математическое ожидание, если оно
существует, определяют формулой
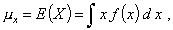
где интеграл берут по всему интервалу
(интервалам) изменения Х.
|
en expectation; expected value; mean
fr esperance mathematique; valeur esperee; moyenne
|
|
1.19. маргинальное математическое ожидание
Математическое ожидание маргинального
распределения случайной величины.
|
en marginal expectation
fr esperance mathematique marginale
|
|
1.20. условное математическое ожидание
Математическое ожидание условного распределения
случайной величины.
|
en conditional expectation
fr esperance mathematique conditionnelle
|
|
1.21. центрированная случайная величина
Случайная величина, математическое ожидание
которой равно нулю.
Примечание - Если случайная величина Х имеет
математическое ожидание m, то соответствующая центрированная случайная
величина равна X - m.
|
en centered random variable
fr variable aleatoire centree
|
|
1.22. дисперсия (случайной величины)
Математическое ожидание квадрата центрированной
случайной величины
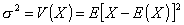
|
en variance
fr variance
|
|
1.23. стандартное отклонение (случайной
величины)
Положительный квадратный корень из значения
дисперсии
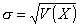
|
en standard deviation
fr ecart-type
|
|
1.24. коэффициент вариации (случайной
величины)
Отношение стандартного отклонения к абсолютному
значению математического ожидания случайной величины
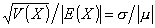
|
en coefficient
of variation
fr coefficient de variation
|
|
1.25. стандартизованная случайная величина
Случайная величина, математическое ожидание
которой равно нулю, а стандартное отклонение - единице.
Примечания
1.
Если случайная величина X имеет математическое ожидание m и стандартное отклонение s, то соответствующая стандартизованная случайная
величина равна
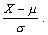
Распределение
стандартизованной случайной величины называется стандартным распределением.
2. Понятие стандартизованной случайной величины является
частным случаем «приведенной случайной величины», определяемой относительно
центрального значения и параметра масштаба, отличных от математического
ожидания и стандартного отклонения.
|
en standardized random variable
fr variable aleatoire centree reduite
|
|
1.26. момент1) порядка q
относительно начала отсчета
Математическое ожидание случайной величины в
степени q для одномерного распределения
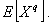
Примечание - Момент первого порядка - математическое
ожидание случайной величины Х.
|
en moment of order q about the origin
fr moment d’ordre q par rapport a l’origine
|
|
1.27. момент1) порядка q
относительно а
Математическое ожидание величины (X - а)
в степени q для одномерного распределения
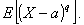
|
en moment of order q about an origin a
fr moment d’ordre q a partir d’une origine a
|
|
1.28. центральный момент порядка q
Математическое ожидание центрированной случайной
величины для одномерного распределения
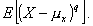
Примечание - Центральный момент второго порядка - дисперсия
случайной величины Х.
|
en central moment of order q
fr moment centre d’ordre q
|
|
1.29. совместный момент1) порядков
q и s относительно начала отсчета
Математическое ожидание произведения случайной
величины Х в степени q и случайной величины Y в степени s для двумерного распределения
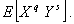
Примечание -
Совместный момент порядков 1 и 0 - маргинальное математическое ожидание
случайной величины X.
Совместный момент порядков 0 и 1 - маргинальное
математическое ожидание случайной величины Y.
|
en joint moment of orders q and s about the origin
fr moment d’ordres q et s a partir de l’origine
|
|
1.30. совместный момент1) порядков
q и s относительно точки (а, b)
Математическое ожидание произведения случайной величины
(X - а) в степени q и случайной величины (Y - b) в степени s для двумерного
распределения:
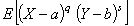
|
en joint moment of orders q and s about an origin (a,
b)
fr moment d’ordres q et s a partir d’une origine (a,
b)
|
|
1.31. совместный центральный момент1)
порядков q и s
Математическое ожидание произведения
центрированной случайной величины (X - mx) в степени q и центрированной случайной
величины (Y - my)в степени s для двумерного
распределения:
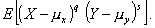
Примечание - Совместный
центральный момент порядков 2 и 0 - дисперсия маргинального распределения X.
Совместный
центральный момент порядков 0 и 2 - дисперсия маргинального распределения Y.
1) Если
при определении моментов значения случайных величин X, X - a,
Y, Y - b и т.д. заменяют на их абсолютные значения |Х|,
|Х - а|, |Y|, |Y - b| и т.д., то моменты
называют «абсолютными моментами».
|
en joint central moment of orders q and s
fr moment centre d’ordres q et s
|
|
1.32. ковариация; корреляционный
момент
Совместный центральный момент порядков 1 и 1:
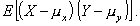
|
en covariance
fr covariance
|
|
1.33. коэффициент корреляции
Отношение ковариации двух случайных величин к
произведению их стандартных отклонений:
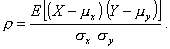
Примечания
1. Эта
величина всегда будет принимать значения от минус 1 до плюс 1, включая
крайние значения.
2. Если две случайные величины независимы, коэффициент корреляции между
ними равен нулю только в случае двумерного нормального распределения.
|
en correlation coefficient
fr coefficient de correlation
|
|
1.34. кривая
регрессии (Y по X)
Для двух случайных
величин Х и Y кривая, отображающая зависимость условного
математического ожидания случайной величины Y при условии Х
= х для каждой переменной х.
Примечание - Если кривая
регрессии Y по X представляет собой прямую линию, то регрессию называют «простой
линейной». В этом случае коэффициент линейной регрессии Y по Х - это коэффициент наклона перед х в уравнении линии
регрессии.
|
en regression
curve
fr courbe de regression
|
|
1.35. поверхность
регрессии (Z по Х и Y)
Для трех случайных
величин X, Y, Z поверхность, отображающая зависимость
условного математического ожидания случайной величины Z при условии Х
= х и Y = y для каждой пары переменных (х, у).
Примечания
1. Если поверхность регрессии
представляет собой плоскость, то регрессию называют «линейной». В этом случае
коэффициент линейной регрессии Z по Х - это коэффициент перед х
в уравнении регрессии.
2. Определение можно распространить на число случайных величин более
трех.
|
en regression
surface
fr surface de regression
|
|
1.36. равномерное
распределение; прямоугольное распределение
а) Распределение вероятностей
непрерывной случайной величины, плотность распределения вероятности которой
постоянна на конечном интервале [а, b] и равна нулю вне
его.
b) Распределение вероятностей дискретной случайной
величины такое, что
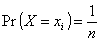
для i = 1, 2, ..., n.
Примечание - Равномерное
распределение дискретной случайной величины имеет равные вероятности для
каждого из п значений, то есть
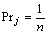
для j = 1, 2, ..., n.
|
en uniform
distribution; rectangular distribution
fr loi uniforme; loi rectangulare
|
|
1.37. нормальное
распределение; распределение Лапласа - Гаусса
Распределение
вероятностей непрерывной случайной величины Х такое, что плотность
распределения вероятностей при - ¥ < х < + ¥ принимает действительное значение
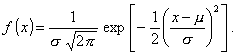
Примечание - m - математическое ожидание; s - стандартное отклонение нормального распределения.
|
en normal
distribution; Laplace - Gauss distribution
fr loi normale; loi de Laplace -
Gauss
|
|
1.38. стандартное
нормальное распределение; стандартное распределение Лапласа - Гаусса
Распределение
вероятностей стандартизованной нормальной случайной величины U,
плотность распределения которой
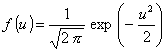
при - ¥ < u < + ¥ (п. 1.25, примечание 1).
|
en standardized
normal distribution; standardized Laplace - Gauss distribution
fr loi normale reduite; loi de
Laplace - Gauss reduite
|
|
1.39. распределение c2
Распределение вероятностей непрерывной случайной
величины, принимающей значения от 0 до + ¥, плотность
распределения вероятностей которой
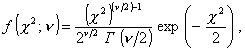
где c2 ³ 0 при
значении параметра n = 1,
2,...;
Г - гамма-функция.
Примечания
1.
Сумма квадратов n независимых стандартизованных нормальных
случайных величин образует случайную величину c2 с параметром n; n называют степенью свободы случайной величины c2.
2. Распределение вероятностей случайной величины c2/2 - это гамма-распределение с параметром m = n/2.
|
en chi-squared distribution; c2-distribution
fr loi de chi carre; loi de c2
|
|
1.40. t-распределение; распределение
Стьюдента
Распределение вероятностей непрерывной случайной
величины, плотность распределения вероятностей которой

где - ¥ < t < + ¥ с
параметром n = 1,
2,...;
Г - гамма-функция.
Примечание - Отношение двух независимых случайных величин,
числитель которого - стандартизованная нормальная случайная величина, а
знаменатель - положительное значение квадратного корня из частного от деления
случайной величины c2 на ее число степеней свободы n - это распределение Стьюдента с v степенями
свободы.
|
en t-distribution; Students distribution
fr loi de t; loi de Student
|
|
1.41. F-распределение
Распределение вероятностей непрерывной случайной
величины, принимающей значения от 0 до +°о, плотность распределения
вероятностей которой
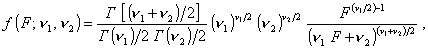
где F ³ 0 с
параметрами n1 = 1,
2,...; n2 = 1,
2,...;
Г - гамма-функция.
Примечание - Это распределение отношения двух независимых
случайных величин с распределениями c2, в котором делимое и делитель разделены на свои
числа степеней свободы. Число степеней свободы числителя равно n1, а знаменателя - n2. В таком порядке и записывают числа степеней свободы случайной величины
с распределением F.
|
en F-distribution
fr loi de F
|
|
1.42 логарифмически нормальное распределение
Распределение вероятностей непрерывной случайной
величины X, которая может принимать любые значения от а до + ¥ и
плотность распределения вероятности которой
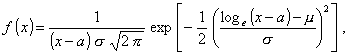
где x > a;
m и s -
соответственно математическое ожидание и стандартное отклонение случайной
величины 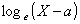 . .
Примечания
1.
Распределение вероятностей случайной величины 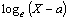 - это нормальное
распределение; m и s - соответственно математическое ожидание и
стандартное отклонение этой случайной величины. - это нормальное
распределение; m и s - соответственно математическое ожидание и
стандартное отклонение этой случайной величины.
2.
Параметры m и s - это не логарифмы математического ожидания и
стандартного отклонения X.
3.
Часто вместо обозначения loge (или ln) используют log10. В этом случае
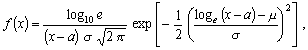
где m и s - соответственно математическое ожидание и
стандартное отклонение 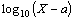 ; ;
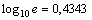
|
en log-normal distribution
fr loi log-normale
|
|
1.43. экспоненциальное
распределение
Распределение
вероятностей непрерывной случайной величины X, которая может принимать
любые значения от 0 до + ¥ и плотность распределения которой
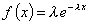
при х ³ 0 и параметре 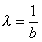 , ,
где b -
параметр масштаба.
Примечание - Такое
распределение вероятностей можно обобщить подстановкой (х - а)
вместо х при х ³ а.
|
en exponential
distribution
fr loi exponentielle
|
|
1.44. гамма-распределение
Распределение
вероятностей непрерывной случайной величины X, которая может принимать
любые значения от 0 до + ¥ и плотность вероятности которой
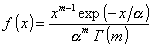
при х ³ 0 и параметрах m > 0, a > 0;
где Г -
гамма-функция
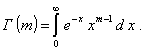
Примечания
1. При m целом имеем:
Г (m) = (m - 1)!
2. Параметр m определяет форму распределения. При m = 1 гамма-распределение превращается в экспоненциальное распределение.
3. Сумма m независимых случайных величин, подчиняющихся экспоненциальному закону
распределения с параметром 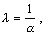 - это
гамма-распределение с параметрами m и a. - это
гамма-распределение с параметрами m и a.
|
en gamma
distribution
fr loi gamma
|
|
1.45. бета-распределение
Распределение
вероятностей непрерывной случайной величины X, которая может принимать
любые значения от 0 до 1, включая границы, и плотность распределения которой
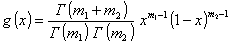
при 0 £ x £ 1 и
параметрах m1 > 0, m2 > 0,
где Г - гамма-функция.
Примечание - При m1 = m2 = 1 бета-распределение переходит в равномерное распределение с
параметрами a = 0 и b = 1.
|
en beta
distribution
fr loi beta
|
|
1.46. распределение Гумбеля; распределение
экстремальных значений типа I
Распределение вероятностей непрерывной случайной
величины Х с функцией распределения:
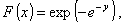
где - ¥ < х
< + ¥;
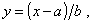
а параметры - ¥ < a < + ¥, b > 0.
|
en Gumbel distribution; type I extreme value distribution
fr loi de Gumbel; loi des valeurs extremes de type I
|
|
1.47. распределение Фрешэ; распределение
экстремальных значений типа II
Распределение вероятностей непрерывной случайной
величины Х с функцией распределения:
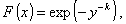
где х ³ а;
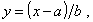
а параметры
- ¥ < a < + ¥, k > 0, b > 0.
Примечание - Параметр k определяет форму
распределения.
|
en Frechet distribution; type II extreme value distribution
fr loi de Frechet; loi des valeurs extremes de type II
|
|
1.48. распределение Вейбулла; распределение
экстремальных значений типа III
Распределение вероятностей непрерывной случайной
величины Х с функцией распределения:
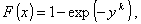
где х ³ а; y = (x - a)/b;
а параметры
- ¥ < a < + ¥, k > 0, b > 0.
Примечание - Параметр k определяет форму
распределения
|
en Weibull distribution; tupe III extreme value distribution
fr loi de Weibull; loi des valeurs extremes de type III
|
|
1.49. биномиальное распределение
Распределение вероятностей дискретной случайной величины
X, принимающей любые целые значения от 0 до n, такое что
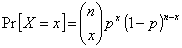
при х
= 0, 1, 2,..., n
и
параметрах n = 1, 2,...
и 0 < p < 1,
где 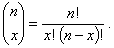
|
en binomial distribution
fr loi binomiale
|
|
1.50. отрицательное биномиальное
распределение
Распределение вероятностей дискретной случайной
величины Х такое, что
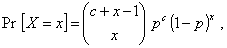
при x = 0, 1, 2,
…
и параметрах c > 0
(целое положительное число), 0 < p < 1,
где 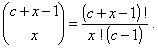
Примечания
1.
Название «отрицательное биномиальное распределение» связано с тем, что
последовательные вероятности при х = 0, 1, 2, … получают при
разложении бинома с отрицательным показателем степени (- с):
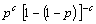
последовательных
положительных целых степеней величины (1 - р).
2. Когда параметр с равен 1, распределение
называют геометрическим распределением.
|
en negative binomial distribution
fr loi binomiale negative
|
|
1.51. распределение Пуассона
Распределение вероятностей дискретной случайной
величины Х такое, что
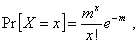
при х = 0, 1, 2, ... и параметре m > 0.
Примечания
1.
Математическое ожидание и дисперсия распределения Пуассона оба равны
параметру m.
2. Распределение Пуассона можно использовать для
аппроксимации биномиального распределения, когда n -
велико, p - мало, а произведение пр = m.
|
en Poission distribution
fr loi de Poisson
|
|
1.52. гипергеометрическое распределение
Дискретное распределение вероятностей с функцией
распределения:
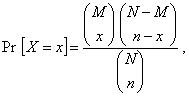
где х = max (0, М
- N + n), ..., max (0, М - N + n) + 1, ..., min (М,
n); параметры N = 1,
2,...;
М = 0, 1, 2, ..., N;
n = 1, 2,..., N
и
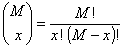 и т.п. и т.п.
Примечание - Это распределение возникает как распределение
вероятностей числа успехов в выборке объема n,
взятой без возвращения из генеральной совокупности объема N,
содержащий М успехов.
|
en hypergeometric distribution
fr loi hypergeometrique
|
|
1.53. двумерное нормальное распределение;
двумерное распределение Лапласа - Гаусса
Распределение вероятностей двух непрерывных
случайных величин Х и Y такое, что
плотность распределения вероятностей
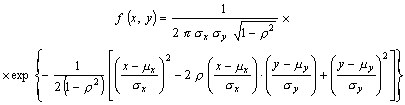
при - ¥ < x
< + ¥ и - ¥ < у
< + ¥,
где mx и my - математические ожидания;
sx и sy - стандартные отклонения маргинальных
распределений Х и Y, которые
нормальны;
r -
коэффициент корреляции Х и Y.
Примечание - Это понятие можно распространить на многомерное
распределение более двух случайных величин таких, что маргинальное
распределение любой их пары может быть представлено в той форме, что
приведена выше.
|
en bivariate normal distribution; bivariate Laplace - Gauss
distribution
fr loi normale a deux variables; loi de Laplace - Gauss a deux
variables
|
|
1.54 стандартизованное двумерное нормальное
распределение; нормированное двумерное распределение Лапласа- Гаусса
Распределение вероятностей пары
стандартизованных нормальных случайных величин
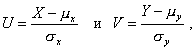
с плотностью распределения
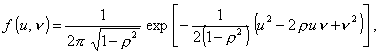
где - ¥ < u < + ¥ и - ¥ < v
< + ¥,
(X, Y) - пара
нормальных случайных величин с параметрами (mx, my) и (sx, sy) и r;
r -
коэффициент корреляции Х и Y, а также U и V.
Примечание - Это понятие можно распространить на
многомерное распределение более двух случайных величин, таких что
маргинальное распределение любой их пары может быть представлено в той же
форме, что приведена выше.
|
en standardized bivariate normal distribution; standardized
bivariate Laplace - Gauss distribution
fr loi normale reduite a deux variables; loi de Laplace - Gauss
reduite a deux variables
|
|
1.55. распределение многомерной случайной
величины; мультиномиальное распределение
Распределение вероятностей k дискретных
случайных величин Х1, Х2, ..., Хk такое, что
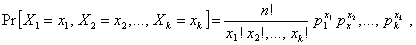
где x1, x2, ..., xk - целые числа, такие что x1 + x2 + ... + xk = n,
с параметрами pi ³ 0 (i = 1, 2,..., k) и 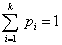 , ,
где k = 2, 3, ...
Примечание - Распределение многомерной случайной величины -
обобщение биномиального распределения (п.
1.49) на распределение k > 2 случайных
величин.
|
en multinomial distribution
fr loi multinomiale
|
|
|
|
|
2.1. единица [объект]
То, что можно рассмотреть и описать
индивидуально.
Примечание - Единицей может, например, быть:
-
изделие;
-
определенное количество материала;
-
услуга, действие или процесс;
- организация
или человек;
- некоторая их комбинация.
|
en item; entity
fr individu; entite
|
|
2.2. признак
Свойство, которое помогает идентифицировать или
различать единицы данной генеральной совокупности.
Примечание - Признак может быть количественным или
качественным (альтернативным).
|
en characteristic
fr caractere
|
|
2.3. (генеральная) совокупность
Множество всех рассматриваемых единиц.
Примечание - Для случайной величины распределение
вероятностей рассматривают как определение совокупности этой случайной
величины.
|
en population
fr population
|
|
2.4. рамки отбора
Список, заполняемый для выборочных целей, в
котором отмечают те единицы, которые надо отобрать и исследовать.
|
en sampling frame
fr base d’echantillonnage
|
|
2.5. подсовокупность
Определенная часть генеральной совокупности.
|
en subpopulation
fr sous-population
|
|
2.6. наблюдаемое значение
Значение данного признака, полученного в
результате единичного наблюдения (см. п. 3.6).
|
en observed value
fr valeur observee
|
|
2.7. класс
а) Для качественного признака - Определенные
группы объектов, каждые из которых имеют отдельные общие признаки, взаимно
исключают друг друга, исчерпывая все объекты.
b) Для
количественного признака - Каждый из последовательных взаимоисключающих
интервалов, на которые разделен весь интервал варьирования.
|
en class
fr classe
|
|
2.8. границы класса; пределы класса
Значения, определяющие верхнюю и нижнюю границы
класса.
Примечания
1. Следует
уточнить, какую из двух границ считают принадлежащей классу.
2. Если возможно, надо чтобы граница класса не
совпадала с возможным значением.
|
en class
limits; class boundaries
fr limites de classe; frontieres de classe
|
|
2.9. середина класса
Среднее арифметическое верхней и нижней границ
класса для количественного признака.
|
en mid-point of class
fr centre de classe
|
|
2.10. интервал класса
Разница между верхней и нижней границами класса
для количественного признака.
|
en class width
fr largeur de classe
|
|
2.11. частота
Число наступлений события данного типа или число
наблюдений, попавших в данный класс.
|
en frequency
fr effectif
|
|
2.12. накопленная кумулятивная частота
Число наблюдений из множества, имеющих значения,
которые меньше заданного значения или равны ему.
Примечание - Для данных, объединенных в классы,
кумулятивную частоту можно указать только в границах класса.
|
en cumulative frequency
fr effectif cumule
|
|
2.13. относительная частота
Частота, деленная на общее число событий или
наблюдений.
|
en relative frequency
fr frequence
|
|
2.14. кумулятивная относительная частота
Кумулятивная частота, деленная на общее число
наблюдений.
|
en cumulative relative frequency
fr frequence cumule
|
|
2.15. распределение частот
Эмпирическое отношение между значениями признака
и его частотами или его относительными частотами.
Примечание - Это распределение можно представить графически
в виде гистограммы, столбиковой диаграммы, полигона кумулятивных частот или
как таблицу сопряженности двух признаков.
|
en frequency distribution
fr distribution d’effectif
|
|
2.16. одномерное распределение частот
Распределение частот для единственного признака.
|
en univariate frequency distribution
fr distribution d’effectif a une variable
|
|
2.17. гистограмма
Графическое представление распределения частот
для количественного признака, образуемое соприкасающимися прямоугольниками,
основаниями которых служат интервалы классов, а площади пропорциональны
частотам этих классов.
|
en histogram
fr histogramme
|
|
2.18. столбиковая диаграмма
Графическое представление распределения частот
для дискретной случайной величины, образуемое набором столбцов равной ширины,
высоты которых пропорциональны частотам.
|
en bar chart; bar diagram
fr diagramme en batons
|
|
2.19. полигон кумулятивных частот
Ломаная линия, получаемая при соединении точек,
абсциссы которых равны верхним границам классов, а ординаты - либо
кумулятивным абсолютным частотам, либо кумулятивным относительным частотам.
|
en cumulative frequency polygon
fr polygone d’effectif cumule
|
|
2.20. двумерное распределение частот
Эмпирическое отношение между парами значений или
классами признаков с одной стороны, и их частотами с другой - для двух признаков,
рассматриваемых одновременно.
|
en bivariate frequency distribution
fr distribution d’effectif a deux variables
|
|
2.21. диаграмма разброса [рассеяния]
Графическое представление множества точек,
координаты которых х и у в обычной прямоугольной системе
координат - это значения признаков Х и Y.
Примечания
1.
Множество из n элементов таким образом дает n
точек, которые наглядно показывают зависимость между Х и Y.
2. Концепцию диаграммы разброса можно распространить
на более чем два признака.
|
en scatter diagram
fr nuage de points
|
|
2.22. таблица сопряженности двух признаков
Таблица, используемая для представления
распределения двух признаков, в строках и столбцах которой указывают,
соответственно, значения или классы первого и второго признаков, при этом на
пересечении строки и столбца появляется частота, соответствующая данной
комбинации значений или классов.
Примечание - Это понятие можно распространить на число
признаков более двух.
|
en two-way table of frequencies; contingency table
fr table d’effectifs a double entree, tableau de contingence
|
|
2.23. многомерное распределение частот
Эмпирическое отношение между совместными
наборами значений или классов признаков с одной стороны и их частотами с
другой - для нескольких признаков, рассматриваемых одновременно.
|
en multivariate frequency distribution
fr distribution d’effectif a plusieurs variables
|
|
2.24. маргинальное распределение частот
Распределение частот подмножества k1 < k признаков из
многомерного распределения частот k признаков, когда остальные (k
- k1) переменных принимают любые значения из своих областей
значений.
Примечания
1. Для
k = 2 признаков маргинальное распределение частот можно получить,
добавляя к каждому значению или классу значений рассматриваемого признака
соответствующие частоты или относительные частоты остальных признаков.
2. В
распределении частот трех признаков X, Y и Z
существуют:
- три
двумерных маргинальных распределения частот, то есть распределения пар (X,
Y), (X, Z), (Y, Z);
- три одномерных маргинальных распределения
частот, то есть распределения X, Y и Z.
|
en marginal frequency distribution
fr distribution d’effectif marginale
|
|
2.25. условное распределение частот
Распределение частот k1 < 1
признаков из многомерного распределения частот, когда остальные (k - k1) признаков фиксированы.
Примечания
1. Для
k = 2 признаков условные распределения частот считывают
непосредственно из строк и столбцов таблицы сопряженности двух признаков.
Условное распределение относительных частот получают делением чисел в каждой
строке (столбце) на общее число в соответствующей строке (столбце).
2. В
распределении частот двух признаков Х и Y:
-
условное распределение частот X; конкретные распределения выражают как
распределение X при Y = у;
- условное распределение частот Y;
конкретные распределения выражают как распределение Y при Х = х.
|
en conditional frequency distribution
fr distribution d’effectif conditionnelle
|
|
2.26. среднее арифметическое
Сумма значений, деленная на их число.
Примечания
1.
Термин «среднее» обычно используют, когда имеют в виду параметр совокупности,
а термин «среднее арифметическое» - когда имеют в виду результат вычислений
по данным, полученным из выборок.
2. Среднее арифметическое простой случайной
выборки, взятой из совокупности, - это несмещенная оценка арифметического
среднего генеральной совокупности. Однако другие формулы для оценки, такие
как геометрическое или гармоническое среднее, медиана или мода, иногда тоже
используют.
|
en arithmetic mean
fr moyenne arithmetique; moyenne
|
|
2.27. взвешенное среднее арифметическое
Сумма произведений каждого значения на его вес, деленная
на сумму весов, где веса - неотрицательные коэффициенты, связанные с каждым
значением.
|
en arithmetic weighted mean
fr moyenne arithmetique ponderee; moyenne ponderee
|
|
2.28. выборочная медиана
Если n случайных
значений упорядочены по возрастанию и пронумерованы от 1 до n, то, если n нечетно,
выборочная медиана принимает значение с номером 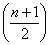 ; если n четно,
медиана лежит между ; если n четно,
медиана лежит между 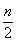 -м и -м и 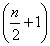 -м значениями и не может быть однозначно определена. -м значениями и не может быть однозначно определена.
Примечание - При отсутствии других указаний и четном n за
выборочную медиану можно принять среднее арифметическое этих двух значений.
|
en sample median
fr mediane
|
|
2.29. середина
размаха (выборки)
Среднее арифметическое
между наибольшим и наименьшим наблюденными значениями количественного
признака.
|
en mid-range
fr milieu de l’etendue
|
|
2.30. размах
(выборки)
Разность между
наибольшим и наименьшим наблюденными значениями количественного признака в
выборке.
|
en range
fr etendue
|
|
2.31. средний
размах (выборок)
Среднее арифметическое
размахов множества выборок одинакового объема.
|
en average range;
mean range
fr etendue moyenne
|
|
2.32. среднее
отклонение (выборки)
Среднее арифметическое
отклонение от начала координат, когда все отклонения имеют положительный
знак.
Примечание - Обычно
выбранное начало отсчета представляет собой среднее арифметическое, хотя
среднее отклонение минимизируется, когда за начало отсчета принимают медиану.
|
en mean deviation
fr ecart moyen
|
|
2.33. выборочная
дисперсия
Одна из мер рассеяния,
представляющая собой сумму квадратов отклонений наблюдений от их среднего
арифметического, деленная на число наблюдений минус единица.
Примечания
1. Для серии из n наблюдений х1,
x2, ..., хn со средним арифметическим
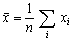
выборочная дисперсия
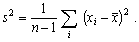
2. Выборочная дисперсия - это
несмещенная оценка дисперсии совокупности.
3. Выборочная дисперсия - это центральный момент второго порядка, кратный
n/(n - 1) (п. 2.39, примечание).
|
en sampling
variance
fr variance
|
|
2.34. выборочное
стандартное отклонение
Положительный квадратный
корень из выборочной дисперсии.
Примечание - Выборочное
стандартное отклонение - это смещенная оценка стандартного отклонения
совокупности.
|
en sampling
standard deviation
fr ecart-type
|
|
2.35. выборочный
коэффициент вариации (Ндп. относительное стандартное отклонение)
Отношение выборочного
стандартного отклонения к среднему арифметическому для неотрицательных
признаков.
Примечание - Это
отношение можно выразить в процентах.
|
en sample
coefficient of variation
fr coefficient de variation
|
|
2.36. выборочный момент порядка q
относительно начала отсчета
Среднее арифметическое наблюдаемых значений в
степени q в распределении единственного признака:
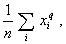
где n - общее
число наблюдений.
Примечание - Момент первого порядка - это среднее
арифметическое наблюдаемых значений.
|
en sample moment of order q about the origin
fr moment d’ordre q par rapport a l’origine
|
|
2.37. выборочный центральный момент порядка q
Среднее арифметическое разностей между наблюдаемыми
значениями хi и их
средним арифметическим 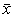 в степени q
в распределении единственного признака: в степени q
в распределении единственного признака:
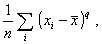
где n - число
наблюдений.
Примечание - Выборочный центральный момент первого порядка
равен нулю.
|
en sample central moment of order q
fr moment centre d’ordre q
|
|
2.38. выборочный совместный момент порядков q
и s относительно начала отсчета
В совместном распределении двух показателей -
среднее арифметическое произведений xi в степени q
и yi в степени s
для всех наблюдаемых пар значений (xi, уi)
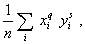
где n - число
наблюдаемых пар.
Примечания
1.
Выборочный совместный момент порядков q и s - это один из
моментов порядка (q + s).
2. Выборочный момент порядков 1 и 0 - это среднее
арифметическое маргинального распределения частот X, а момент порядков
0 и 1 - среднее арифметическое маргинального распределения частот Y.
|
en sample joint moment of orders q and s about the
origin
fr moment d’ordres q et s par rapport a l’origine
|
|
2.39. выборочный совместный центральный
момент порядков q и s
В совместном распределении двух признаков -
среднее арифметическое произведений разности между xi и его средним арифметическим значением 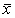 в степени q
и разности между уi и его средним
арифметическим значением в степени q
и разности между уi и его средним
арифметическим значением 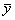 в степени s для всех наблюдаемых пар (xi, уi): в степени s для всех наблюдаемых пар (xi, уi):
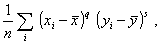
где n - число
наблюдаемых пар.
Примечание - Выборочный центральный момент порядков 2 и 0 -
это выборочная дисперсия маргинального распределения частот X,
умноженная на (n - 1)/n, а
выборочный центральный момент порядков 0 и 2 - выборочная дисперсия
маргинального распределения частот Y, умноженная на (n - 1)/n.
|
en sample joint central moment of orders q and s
fr moment centre d’ordres q
et s
|
|
2.40. выборочная ковариация
Сумма произведений отклонений х и у
от их соответствующих средних арифметических, деленная на число наблюдаемых
пар без единицы:
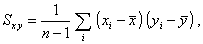
где n - число
наблюдаемых пар.
Примечание - Выборочная ковариация - это несмещенная оценка
ковариации совокупности.
|
en sample covariance
fr covariance
|
|
2.41. выборочный коэффициент корреляции
Частное от деления выборочной ковариации двух
показателей на произведение их выборочных стандартных отклонений:
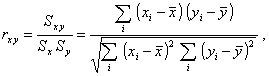
где Sxy -
выборочная ковариация Х и Y;
Sx и Sy - выборочные стандартные отклонения Х и Y соответственно.
Примечания
1.
Этот коэффициент часто используют как цифровое выражение взаимной зависимости
между Х и Y в серии парных наблюдений. Для проверки линейности
можно строить диаграмму разброса.
2. Его
значения всегда лежат между минус 1 и плюс 1. Когда выборочный коэффициент
корреляции равен одному из указанных пределов, это означает, что существует
точная линейная зависимость в серии парных наблюдений.
3. Этот выборочный коэффициент корреляции
применяют для измеряемых признаков; для ранговых данных используют другие
коэффициенты корреляции, такие как коэффициенты Спирмена и Кендалла.
|
en sample correlation coefficient
fr coefficient de correlation
|
|
2.42. кривая регрессии (Y по Х для выборки)
Для выборки n пар
наблюдений двух показателей Х и Y - кривая
регрессии Y от X отображает зависимость функции Y от X.
|
en regression curve
fr courbe de regression
|
|
2.43. поверхность регрессии (Z по Х
и Y для
выборки)
Для выборки п наблюдений каждого из трех
показателей X, Y и Z
- поверхность регрессии Z от Х и Y отображает
зависимость функции Z от X и Y.
Примечание - Вышеуказанные определения можно распространить
также на случай более трех показателей.
|
en regression surface
fr surface de regression
|
|
2.44. выборочный коэффициент регрессии
Коэффициент при переменной в уравнении кривой
или поверхности регрессии.
|
en sample regression coefficient
fr coefficient de regression
|
|
2.45. статистика
Функция от выборочных значений.
Примечание - Статистика как функция от выборочных значений
- случайная величина, которая может принимать различные значения от выборки к
выборке. Значение статистики, получаемое при использовании наблюдаемых
значений, как их функция может быть использовано при проверке статистических
гипотез или как оценка параметра совокупности, например среднего
арифметического или стандартного отклонения.
|
en statistics
fr statistique
|
|
2.46. порядковая статистика
Каждое из упорядоченных выборочных значений,
расположенных в неубывающем порядке.
Примечания
1. В
более общем выражении всякую статистику, основанную на порядковых статистиках
в этом узком смысле, также называют порядковой статистикой.
2. k-e значение в неубывающей
последовательности наблюдений x|k| - это значение случайной величины X|k|, называемое k-й порядковой статистикой. В выборке объема n
наименьшее наблюдаемое значение x|1| и наибольшее значение x|n| - это значения случайных величин X|1| и X|n| - первая и n-я
порядковые статистики соответственно. Размах x|n| - x|1| - это значение порядковой статистики X|n| - X|1|.
|
en order statistics
fr statistique d’ordre
|
|
2.47. тренд
Тенденция к возрастанию или убыванию наблюдаемых
значений, нанесенных на график в порядке их получения после исключения
случайных ошибок и циклических эффектов.
|
en trend
fr tendance
|
|
2.48. серия
а) Появление в рядах наблюдений по качественному
признаку непрерывающихся рядов одного и того же значения признака.
b) Последовательный набор монотонно возрастающих
или монотонно убывающих значений в рядах наблюдений по количественному
признаку.
Примечание - Последовательный набор монотонно возрастающих значений
называют возрастающей серией, а монотонно убывающих значений - убывающей
серией.
|
en run
fr suite
|
|
2.49. оценивание (параметра)
Операция определения на основе выборочных данных
числовых значений параметров распределения, принятого в качестве статистической
модели генеральной совокупности, из которой извлечена выборка.
Примечание - Результат этой операции может быть выражен как
одним числовым значением, так и доверительным интервалом.
|
en estimation
fr estimation
|
|
2.50. оценка
Статистика, используемая для оценивания
параметра совокупности.
|
en estimator
fr estimateur
|
|
2.51. значение оценки
Значение параметра, полученное в результате
оценивания.
|
en estimate
fr estimation (resultat)
|
|
2.52. погрешность оценки
Разность (Т - q) при
оценивании параметра, где T обозначает
результат оценки, а q -
оцениваемый параметр.
Примечание - Погрешность при оценивании может включать в
себя один или несколько из следующих компонентов:
-
погрешность выборочного метода;
-
погрешность измерения;
-
округление значений или разделение на классы;
- другие погрешности.
|
en estimator error
fr erreur d’estimation
|
|
2.53. погрешность выборочного метода
Часть погрешности при оценивании, обусловленная только
тем, что объем выборки меньше, чем объем генеральной совокупности.
|
en sampling error
fr erreur d’echantillonnage
|
|
2.54. смещение оценки
Разность между математическим ожиданием оценки и
значением оцениваемого параметра.
|
en bias of estimator
fr biais d’un estimateur
|
|
2.55. несмещенная оценка
Оценка со смещением, равным нулю.
|
en unbiased estimator
fr estimateur sans biais
|
|
2.56. стандартная ошибка; среднеквадратичная
ошибка
Стандартное отклонение оценки.
|
en standard error
fr erreur-type
|
|
2.57. двусторонний доверительный интервал
Если T1 и T2 - две функции от наблюдаемых
значений таких, что для оценки параметра распределения совокупности q
вероятность 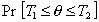 равна (1 - a), где (1 -
a) - константа,
положительная и меньше 1, то интервал между T1 и T2 - это двусторонний
доверительный интервал для q при
доверительной вероятности (1 - a). равна (1 - a), где (1 -
a) - константа,
положительная и меньше 1, то интервал между T1 и T2 - это двусторонний
доверительный интервал для q при
доверительной вероятности (1 - a).
Примечания
1.
Границы T1 и T2 доверительного интервала - это статистики (2.45), которые в общих
предположениях принимают различные значения от выборки к выборке.
2. В длинном ряду выборок относительная частота
случаев, когда доверительный интервал накрывает истинное значение параметра
совокупности q, больше или равна (1 - a).
|
en two-sided confidence interval
fr intervalle de confiance bilateral
|
|
2.58. односторонний доверительный интервал
Если Т - функция от наблюдаемых значений
такая, что для оценки параметра распределения совокупности q
вероятность 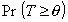 или вероятность или вероятность 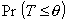 равна (1 - a), где (1 -
a) -
константа, положительная и меньше 1, то интервал от наименьшего возможного
значения q до Т
или интервал от T до
наибольшего возможного значения q - это
односторонний доверительный интервал для q при
доверительной вероятности (1 - a). равна (1 - a), где (1 -
a) -
константа, положительная и меньше 1, то интервал от наименьшего возможного
значения q до Т
или интервал от T до
наибольшего возможного значения q - это
односторонний доверительный интервал для q при
доверительной вероятности (1 - a).
Примечания
1.
Граница T доверительного интервала - это статистика,
которая в общих предположениях принимает различные значения от выборки к
выборке.
2. См. п.
2.57, примечание 2.
|
en one-sided confidence interval
fr intervalle de confiance unilateral
|
|
2.59. доверительная вероятность; уровень
доверия
Величина (1 - a) -
вероятность, связанная с доверительным интервалом или со статистически
накрывающим интервалом.
Примечание - Величину (1 - a) часто выражают в процентах.
|
en confidence coefficient; confidence level
fr niveau de confiance
|
|
2.60. доверительная граница
Каждая из границ, нижняя T1, верхняя T2 для двустороннего
доверительного интервала или граница Т для одностороннего интервала.
|
en confidence limit
fr limite de confiance
|
|
2.61. толерантный интервал
Интервал, для которого можно утверждать с данным
уровнем доверия, что он содержит, по крайней мере, заданную долю определенной
совокупности.
Примечание - Если определены обе границы по статистическим
данным, то интервал двусторонний. Если одна из двух границ представляет собой
бесконечность или ограничение области определения случайной величины, то
интервал односторонний.
|
en statistical coverage interval
fr intervalle statistique de
dispersion
|
|
2.62. толерантные границы
Для двустороннего статистически накрывающего
интервала - нижняя и верхняя границы этого интервала; для одностороннего
статистически накрывающего интервала - значение статистики, ограничивающей
этот интервал.
|
en statistical coverage limits
fr limites statistiques de dispersion
|
|
2.63. критерий согласия распределения
Мера соответствия между наблюдаемым распределением
и теоретическим распределением, выбранным априори либо подобранным по
результатам наблюдений.
|
en goodness of fit of a distribution
fr adequation d’une distribution; validite de l’ajustement
|
|
2.64. выбросы
Наблюдения в выборке, отличающиеся от остальных
по величине настолько, что возникает предположение, что они принадлежат
другой совокупности или получены в результате ошибки измерения.
|
en outliers
fr valeurs aberrantes
|
|
2.65. статистический критерий
Статистический метод принятия решений о том,
стоит ли отвергнуть нулевую гипотезу в пользу альтернативной или нет.
Примечания
1.
Решение о нулевой гипотезе принимают исходя из значений соответствующих
статистик, лежащих в основе статистических критериев или рассчитанных по
результатам наблюдений. Так как статистики - случайные величины, существует
некоторый риск принятия ошибочного решения (п.
2.75 и п.
2.77).
2. Критерий априори предполагает, что проверяют
некоторые предположения, например предположение о независимости наблюдений,
предположение о нормальности и т.д.
|
en statistical test
fr test statistique
|
|
2.66. нулевая гипотеза и альтернативная
гипотеза
Утверждения относительно одного или нескольких
параметров или о распределении, которые проверяют с помощью статистического
критерия.
Примечания
1.
Нулевая гипотеза (Н0) - предположение, обычно сложное,
относят к утверждению, подвергаемому проверке, в то время как альтернативную
гипотезу (Н1) относят к утверждению, которое будет принято,
если нулевую гипотезу отвергают.
2.
Проверка гипотезы о том, что математическое ожидание m случайной величины Х в совокупности не
меньше, чем заданное значение m0:
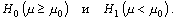
3.
Проверка гипотезы о том, что доли несоответствующих деталей в двух партиях р1
и p2 одинаковы (неодинаковы):
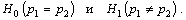
4. Проверка гипотезы о том, что случайная
величина X имеет нормальное распределение с неизвестными параметрами.
Альтернативная гипотеза - распределение не нормально.
|
en null hypothesis and alternative hypothesis
fr hypothese nulle et hypothese alternative
|
|
2.67. простая гипотеза
Гипотеза, которая полностью задает распределение
совокупности.
|
en simple hypothesis
fr hypothese simple
|
|
2.68. сложная гипотеза
Гипотеза, которая не полностью задает
распределение совокупности.
Примечания
1. Это
обычно гипотеза, которая включает в себя бесконечную систему простых гипотез.
2. В предположении
нормального распределения гипотеза m = m0 будет простой, если стандартное отклонение совокупности известно, но она
будет сложной, если оно неизвестно.
3. Все гипотезы из примечаний, приведенных в п.
2.66, сложные.
|
en composite hypothesis
fr hypothese composite
|
|
2.69. свободный от распределения критерий
Критерий, в котором функция распределения
статистики, лежащей в основе критерия, не зависит от функции распределения
наблюдений
|
en distribution-free test
fr test non parametrique
|
|
2.70. уровень значимости (критерия)
Заданное значение верхнего предела вероятности
ошибки первого рода. Примечание- Уровень значимости обычно обозначают а.
|
en significance level
fr niveau de signification
|
|
2.71. критическая область
Множество возможных значений статистики, лежащей
в основе критерия, для которого отвергают нулевую гипотезу.
Примечания
1.
Критические области определяют таким образом, что если нулевая гипотеза
верна, вероятность ее отбрасывания равна заданному значению a, обычно малому, например 5 % или 1 %.
2.
Классический способ проверки нулевой гипотезы, относящийся к математическому
ожиданию нормального распределения с известным стандартным отклонением s, H0 (m ³ m0) против альтернативы H1 (m < m0), - использование статистики 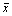 выборочного
среднего арифметического. выборочного
среднего арифметического.
Критическая
область - это множество значений статистики, меньших чем
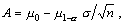
где n -
объем выборки;
m1-a - это квантиль уровня (1 - a) стандартизованной нормальной случайной
величины.
Если рассчитанное значение 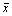 меньше А,
гипотезу Н0 отвергают. В противном случае - Н0
не отвергают (принимают). меньше А,
гипотезу Н0 отвергают. В противном случае - Н0
не отвергают (принимают).
|
en critical region
fr region critique
|
|
2.72. критическое значение
Значение, ограничивающее критическую область.
|
en critical value
fr valeur critique
|
|
2.73. односторонний критерий
Критерий, в котором используемая статистика
одномерна, а критическая область включает в себя множество значений, меньших критического
значения, или множество значений, больших критического значения.
|
en one-sided test
fr test unilateral
|
|
2.74. двусторонний критерий
Критерий, в котором используемая статистика одномерна,
а критическая область состоит из множества значений, меньших первого
критического значения, и множества значений, больших второго критического
значения.
Примечание - Выбор между односторонним и двусторонним
критериями определяется альтернативной гипотезой. В примечании, приведенном в
п. 2.71, критерий односторонний, а критическое значение
равно А.
|
en two-sided test
fr test bilateral
|
|
2.75. ошибка первого рода
Ошибка, состоящая в отбрасывании нулевой
гипотезы, поскольку статистика принимает значение, принадлежащее критической
области, в то время как эта нулевая гипотеза верна.
|
en error of the first kind
fr erreur de premiere espece
|
|
2.76. вероятность ошибки первого рода
Вероятность допустить ошибку первого рода.
Примечания
1. Она
всегда меньше уровня значимости критерия или равна ему.
2. В примечании 2 к п.
2.71 ошибка первого рода состоит в отбрасывании H0 (m < m0), потому что 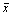 меньше А, в
то время как на самом деле m равно или превышает m0. Вероятность такой ошибки равна a при m = m0 и уменьшается с увеличением m. меньше А, в
то время как на самом деле m равно или превышает m0. Вероятность такой ошибки равна a при m = m0 и уменьшается с увеличением m.
|
en type I error probability
fr probabilite d’erreur de premiere espece
|
|
2.77. ошибка второго рода
Ошибка принять нулевую гипотезу, поскольку
статистика принимает значение, не принадлежащее критической области, в то
время как нулевая гипотеза не верна.
|
en error of the second kind
fr erreur de seconde espece
|
|
2.78. вероятность ошибки второго рода
Вероятность допустить ошибку второго рода.
Примечание - Вероятность ошибки второго рода, обычно
обозначаемая b, зависит от реальной ситуации и может быть
вычислена лишь в том случае, если альтернативная гипотеза задана адекватно.
|
en type II error probability
fr probabilite d’erreur de seconde espece
|
|
2.79. мощность критерия
Вероятность недопущения ошибки второго рода.
Примечания
1. Это
вероятность отбрасывания нулевой гипотезы, когда она не верна. Ее обычно
обозначают (1 - b).
2. В
примечании 2 к п. 2.71
ошибка второго рода состоит в принятии гипотезы H0 (m ³ m0), поскольку 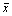 превышает А,
в то время как на самом деле m меньше m0. Вероятность b такой ошибки зависит от фактического значения m: чем ближе m к m0, тем ближе мощность к 1. превышает А,
в то время как на самом деле m меньше m0. Вероятность b такой ошибки зависит от фактического значения m: чем ближе m к m0, тем ближе мощность к 1.
3. В примечании 4 к п.
2.66 проверка нулевой гипотезы H0 (нормально распределенная совокупность) против
альтернативы H1 (совокупность с ненормальным распределением) невозможно выразить b как функцию от альтернативной гипотезы,
поскольку она не определена.
|
en power of a test
fr puissance d’un test
|
|
2.80. функция мощности критерия
Функция, которая определяет мощность критерия,
обычно обозначаемую (1 - b) или (1 - Pa),
при проверке гипотезы относительно значений скалярного параметра.
Примечание - Эта функция, определяемая для значений тех
параметров, которые относятся к соответствующим альтернативным гипотезам,
представляет собой вероятность отклонения нулевой гипотезы, когда она не
верна.
|
en power function of a test
fr fonction de puissance d’un test
|
|
2.81. кривая мощности (критерия)
Графическое представление функции мощности
критерия.
Примечания
1. На рисунке
1 представлена кривая мощности для проверки
гипотезы H0 (m ³ m0) против альтернативной гипотезы H1 (m < m0) в зависимости от математического ожидания совокупности m и уровня значимости критерия a.
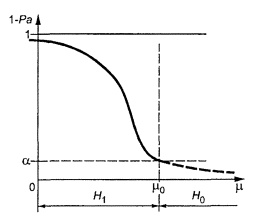
Рисунок 1 - Кривая
мощности
1 - Pa
- вероятность отклонения гипотезы H0; m - математическое ожидание совокупности
2. На рисунке
2 представлена кривая мощности критерия для
гипотезы H0 (p £ p0) против H1 (p > p0) в зависимости от р0 - доли
несоответствующих единиц в партии, проходящей контроль.
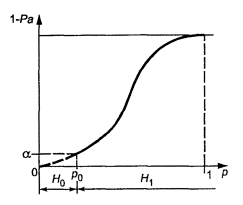
Рисунок 2 - Кривая
мощности
1 - Pa
- вероятность отклонения гипотезы H0; p - доля несоответствующих единиц в партии.
|
en power curve
fr courbe de puissance
|
|
2.82. оперативная характеристика
Функция, которая определяет вероятность принятия
нулевой гипотезы относительно значений скалярного параметра, обычно
обозначаемая Ра.
Примечание - Оперативная характеристика всегда равна
единице минус значение критерия мощности.
|
en operating characteristic
fr efflcacite
|
|
2.83. кривая оперативной характеристики; кривая
ОХ
Графическое представление оперативной
характеристики.
Примечания
1. На рисунке
3 представлена кривая оперативной характеристики
для проверки гипотезы H0 (m ³ m0) против H1 (m < m0) в зависимости от математического ожидания генеральной совокупности m и уровня значимости критерия a.
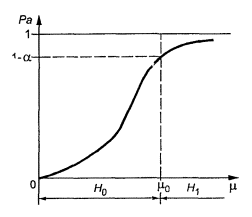
Рисунок 3 - Кривая оперативной характеристики
Pa - вероятность принятия гипотезы H0; m - математическое ожидание совокупности
2. На рисунке
4 представлена кривая оперативной характеристики
для проверки гипотезы H0 (p < p0) против H1 (p ³ p0) в зависимости от р - доли несоответствующих единиц в партии,
проходящей контроль.
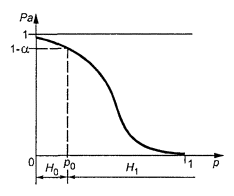
Рисунок 4 - Кривая
оперативной характеристики
Pa - вероятность принятия гипотезы H0; p - доля несоответствующих единиц в партии.
|
en operating characteristic curve
fr courbe d’efficacite
|
|
2.84. значимый результат (на выбранном уровне
значимости a)
Результат статистической проверки, который
приводит к отбрасыванию нулевой гипотезы, в противном случае - результат
незначим.
Примечания
1.
Когда результат проверки называют статистически значимым, это показывает, что
результат выходит за тот диапазон значений, в который укладываются случайные
воздействия, когда нулевая гипотеза верна.
2. Для
примера, приведенного в п. 2.71, при 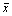 , меньшем А, где , меньшем А, где 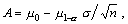 считают, что считают, что 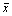 значимо меньше m0 на уровне значимости 1 - a. значимо меньше m0 на уровне значимости 1 - a.
|
en significant result (at the closen significance level a)
fr resultat significatif (an niveau de signification a
choisi)
|
|
2.85. степень свободы
В общем случае число слагаемых минус число
ограничений, налагаемых на них.
|
en degree of freedom
fr degre de liberte
|
|
2.86. c2-критерий
Критерий, в котором в нулевой гипотезе
используемая статистика имеет по предположению распределение c2.
Примечание - Его применяют, например, при решении следующих
задач:
-
проверка равенства дисперсии нормальной совокупности и заданного значения
дисперсии, оцениваемой на основе статистики критерия по выборке, взятой из
этой совокупности;
-
сравнение наблюдаемых частот с теоретическими частотами.
|
en c2-test; chi-squared test
fr test de chi carre; test c2
|
|
2.87. t-критерий; критерий
Стьюдента
Статистический критерий, в котором в нулевой
гипотезе используемая статистика соответствует t-распределению.
Примечание - Этот критерий применяют, например, при решении
следующих задач:
-
проверка равенства математического ожидания нормальной совокупности заданному
значению с помощью критерия, основанного на выборочном среднем и выборочной
дисперсии;
-
проверка равенства математических ожиданий из двух нормальных совокупностей с
одинаковой дисперсией на основе двух выборочных средних и двух выборочных
дисперсий из двух независимых выборок, взятых из этих совокупностей;
-
критерий, применяемый к значению линейной регрессии или коэффициента
корреляции.
|
en t-test; Students test
fr test t; test de Student
|
|
2.88. F-критерий, критерий
Фишера
Статистический критерий, в котором в нулевой
гипотезе используемая статистика имеет по предположению F-распределение.
Примечание - Этот критерий применяют, например, при решении
следующих задач:
-
проверка равенства дисперсий двух нормальных совокупностей на основе
выборочных дисперсий, оцениваемых по двум независимым выборкам;
-
проверка математических ожиданий равенства нескольких (например, К)
нормальных совокупностей с одинаковыми дисперсиями на основе средних
арифметических и выборочных дисперсий независимых выборок.
|
en F-test
fr test F
|
|
2.89. повторение
Термин, обозначающий выполнение статистического
исследования несколько раз одним и тем же методом на одной и той же
совокупности при одинаковых условиях.
|
en repetition
fr repetition
|
|
2.90. реплика; повторное проведение
эксперимента
Определение значений более чем один раз в ходе
эксперимента или исследования.
Примечание -
Реплики отличаются от повторений тем, что предполагают повторные проверки в
разных местах и (или) в разное время в соответствии с планом (по 1.10, ИСО
3534.3).
|
en replication
fr replique
|
|
2.91. рандомизация
Процесс, с помощью которого множество объектов
устанавливают в случайном порядке.
Примечание -
Если из совокупности, состоящей из натуральных чисел от 1 до n,
извлекать числа случайно (то есть таким образом, чтобы все числа имели
одинаковые шансы быть выбранными) одно за другим без возвращения, пока
совокупность не исчерпается, то порядок отбора чисел называют случайным. Если
эти n чисел ассоциировать с n
различными объектами или с n разными обработками (по 1.4, ИСО 3534.3),
которые, таким образом, переупорядочиваются в том порядке, в котором были
вытянуты числа, порядок объектов или обработок называют случайным (по 1.12,
ИСО 3534.3).
|
en randomization
fr randomisation
|
|
2.92. случайные причины
Факторы, каждый из которых играет относительно
малую роль, но создают вариацию, которую нельзя идентифицировать (по ГОСТ Р
50779.11).
|
en chance causes
fr causes aleatoires
|
|
|
|
3.1. (измеримая) величина; физическая
величина
Признак явления, материала или вещества, который
можно различить качественно и определить количественно [п. 1].
Примечания
1.
Термин «величина» может относиться к количеству в общем смысле, например
длина, время, масса, температура, электрическое сопротивление, или к
определенным установленным величинам, например длина определенного стержня,
электрическое сопротивление определенной проволоки.
2.
Величины, которые взаимно сравнимы, можно объединять в количественные
категории, например:
-
работа, тепло, энергия;
-
толщина, периметр, длина волны.
3.
Символы для величин приведены в ИСО 31.0 - ИСО 31.13.
4.
Измеримые величины можно определить количественно.
|
en (measurable) quantity
fr grandeur (measurable)
|
|
3.2. истинное значение (величины)
Значение, которое идеальным образом определяет
величину при тех условиях, при которых эту величину рассматривают [п. 1].
Примечание -
Истинное значение - теоретическое понятие, которое нельзя определить точно.
|
en true value (of a quantity)
fr valeur vraie (d’une qrandeur)
|
|
3.3. действительное значение (величины)
Значение величины, которое для данной цели можно
рассматривать как истинное [п. 1], [п. 2].
Примечания
1.
Действительное значение в общем смысле рассматривают как достаточно близкое к
истинному значению, поскольку разница не имеет большого значения для данной
цели.
2. Значение, приписанное в организации некоторому
эталону, можно рассматривать как действительное значение величины,
воспроизводимой этим эталоном.
|
en conventional true value (of a quantity)
fr valeur conventionnellement vraie
|
|
3.4. принятое нормальное значение
Значение величины, служащее согласованным
эталоном для сравнения и определяемое как:
а) теоретическое или установленное значение,
основанное на научных принципах;
b) принятое или сертифицированное значение,
основанное на экспериментальных данных некоторых национальных или
международных организаций;
с) согласованное (на основе консенсуса) или
сертифицированное значение, основанное на совместной экспериментальной
работе, проводимой научным или инженерным коллективом;
d) когда а), b) и с) не
подходят, математическое ожидание измеримой величины, то есть среднее арифметическое
измерений конкретной совокупности.
|
en accepted reference value
fr valeur de reference acceptee
|
|
3.5. измеряемая величина
Величина, подвергаемая измерению [1], [2].
Примечание - По обстоятельствам это может быть величина,
измеряемая количественно или качественно.
|
en meausurand
fr mesurande
|
|
3.6. наблюдаемое значение
Значение данного признака, полученное в
результате единичного наблюдения (по ИСО 5725.1).
|
en observed value
fr valeur observee
|
|
3.7. результат проверки
Значение некоторого признака, полученное
применением определенного метода проверки.
Примечания
1. Под
проверкой можно понимать такие процедуры, как измерение, испытание, контроль
и т.д.
2. В методе проверки должно быть уточнено, что
будут выполнять одно или несколько индивидуальных наблюдений, что будут
регистрировать в качестве результата проверки - их среднее арифметическое или
иную подходящую функцию, такую как медиана или стандартное отклонение. Может
также потребоваться применить стандартный метод корректировки, например
поправку на объем газа при стандартных температуре и давлении таким образом,
что результат проверки может быть результатом, вычисленным по нескольким
наблюдаемым значениям. В простом случае результат проверки - это само
наблюдаемое значение.
|
en test result
fr resultat d’essai
|
|
3.8. ошибка результата (проверки)
Результат проверки минус принятое нормальное
значение величины (по ИСО 5725.1).
Примечание - Ошибка - это сумма случайных ошибок и
систематических ошибок.
|
en error of result
fr erreur de resultat
|
|
3.9. случайная ошибка результата (проверки)
Компонент ошибки, который изменяется
непредвиденным образом в ходе получения результатов проверки одного признака
(по ИСО 5725.1).
Примечание - Случайную ошибку результата проверки
нельзя скорректировать.
|
en random error of result
fr erreur aleatoire de resultat
|
|
3.10. систематическая ошибка результата
(проверки)
Компонент ошибки результата, который остается
постоянным или закономерно изменяется в ходе получения результатов проверки
для одного признака.
Примечание - Систематические ошибки и их причины могут быть
известны или неизвестны.
|
en systematic error of result
fr erreur systematique de resultat
|
|
3.11. точность (результата проверки)
Близость результата проверки к принятому
нормальному значению величины (по ИСО 5725.1).
Примечание - Понятие точности, когда его относят к
результатам проверки, включает в себя комбинацию случайных компонентов и
общего компонента систематической ошибки или смещения.
|
en accuracy
fr exactitude
|
|
3.12. правильность (результата проверки)
Близость среднего значения, полученного в
длинном ряду результатов проверок, к принятому нормальному значению величины
(по ИСО 5725.1).
Примечание - Меру правильности обычно выражают в терминах
смещения.
|
en trueness
fr justesse
|
|
3.13. смещение (результата проверки)
Разность между математическим ожиданием
результатов проверки и принятым нормальным значением (по ИСО 5725.1).
Примечание - Смещение - это общая систематическая ошибка в
противоположность случайной ошибке. Может быть один или несколько
компонентов, образующих систематическую ошибку. Большее систематическое
смещение от принятого значения соответствует большому значению смещения.
|
en bias
fr biais
|
|
3.14. прецизионность (результата проверки)
Близость между независимыми результатами
проверки, полученными при определенных принятых условиях (по ИСО 5725.1).
Примечания
1.
Прецизионность зависит от распределения случайных ошибок и не связана ни с
истинным значением, ни с заданным значением.
2.
Меру прецизионности обычно выражают в терминах рассеяния и вычисляют как
стандартное отклонение результатов проверки. Малой прецизионности
соответствует большое стандартное отклонение.
3. Независимые результаты проверки означают
результаты, полученные таким образом, что отсутствует влияние предыдущих
результатов на том же самом или аналогичном объекте проверки. Количественные
меры прецизионности решающим образом зависят от принятых условий. Условия
повторяемости и воспроизводимости являются разными степенями принятых
условий.
|
en precision
fr fidelite
|
|
3.15. повторяемость (результата проверки);
сходимость
Прецизионность в условиях повторяемости (по ИСО
5725.1)
|
en repeatability
fr repetabilite
|
|
3.16. условия повторяемости
Условия, при которых независимые результаты
проверки получены одним методом, на идентичных испытательных образцах, в
одной лаборатории, одним оператором, с использованием одного оборудования и
за короткий интервал времени (по ИСО 5725.1).
|
en repeatability conditions
fr conditions de repetabilite
|
|
3.17. стандартное отклонение повторяемости
Стандартное отклонение результатов проверки,
полученных в условиях повторяемости (по ИСО 5725.1).
Примечания
1. Это
мера рассеяния результатов проверки в условиях повторяемости.
2. Аналогично «дисперсию повторяемости» и
«коэффициент вариации повторяемости» надо определять как меры рассеяния
результатов проверки в условиях повторяемости.
|
en repeatability standard deviation
fr ecart-type de repetabilite
|
|
3.18. предел повторяемости
Значение, которое меньше или равно абсолютной
разности между двумя результатами проверок, получаемыми в условиях
повторяемости, ожидаемое с вероятностью 95 % (по ИСО 5725.1).
Примечания
1.
Используют обозначение r.
2. В настоящее время в нормативных документах
принято обозначение d.
|
en repeatability limit
fr limite de repetabilite
|
|
3.19. критическая разность повторяемости
Значение, меньшее или равное абсолютной разности
между двумя конечными значениями, каждое из которых представляет собой ряды
результатов проверок, полученных в условиях повторяемости, ожидаемое с
заданной вероятностью (по ИСО 5725.1).
Примечания
1.
Примерами конечных результатов служат среднее арифметическое и выборочная
медиана рядов результатов проверок; сами ряды могут содержать только по
одному результату проверки.
2. Предел повторяемости r - это
критическая разность повторяемости для двух единичных результатов проверки
при вероятности 95 %.
|
en repeatability critical difference
fr difference critique de repetabilite
|
|
3.20. воспроизводимость (результатов
проверки)
Прецизионность в условиях воспроизводимости (по
ИСО 5725.1).
|
en reproducibility
fr reproductibilite
|
|
3.21. условия воспроизводимости
Условия, при которых результаты проверки получены
одним методом, на идентичных испытательных образцах, в различных
лабораториях, разными операторами, с использованием различного оборудования
(по ИСО 5725.1).
|
en reproducibility conditions
fr conditions de reproductibilite
|
|
3.22. стандартное отклонение
воспроизводимости
Стандартное отклонение результатов проверки,
полученных в условиях воспроизводимости.
Примечания
1. Это
мера рассеяния распределения результатов проверки в условиях
воспроизводимости.
2. Аналогично «дисперсию воспроизводимости» и
«коэффициент вариации воспроизводимости» надо определять как меры рассеяния
результатов проверки в условиях воспроизводимости.
|
en reproducibility standard deviation
fr ecart-type de reproductibilite
|
|
3.23. предел воспроизводимости
Значение, меньшее или равное абсолютной разности
между двумя результатами проверки, полученными в условиях воспроизводимости,
ожидаемое с вероятностью 95 % (по ИСО 5725.1).
Примечания
1.
Используют обозначение R.
2. В настоящее время в нормативных документах
принято обозначение D.
|
en reproducibility limit
fr limite de reproductibilite
|
|
3.24. критическая разность воспроизводимости
Значение, меньшее или равное абсолютной разности
между двумя конечными значениями, каждое из которых представляет собой ряды
результатов проверок, полученных в условиях воспроизводимости, ожидаемое с
заданной вероятностью (по ИСО 5725.1).
Примечание - Примерами конечных результатов служат среднее
арифметическое и выборочная медиана рядов результатов проверок; ряды могут
содержать только по одному результату проверки.
|
en reproducibility critical difference
fr difference critique de reproductibilite
|
|
3.25. неопределенность (результата проверки)
Оценка, относящаяся к результату проверки,
которая характеризует область значений, внутри которой лежит истинное
значение.
Примечания
1.
Неопределенность измеряет совокупность многих компонентов. Некоторые из них
можно оценить на основе статистического распределения результатов в рядах измерений
и охарактеризовать стандартными отклонениями. Оценки других компонентов
возможны только на основе опыта или из других источников информации.
2.
Неопределенность следует отличать от оценки, связанной с результатом
проверки, которая характеризуется значениями интервалов, внутри которых лежит
математическое ожидание. Эта последняя оценка - мера прецизионности, а не
правильности, и ее надо использовать, только если истинное значение не
определено. Когда математическое ожидание используют вместо истинного
значения, надо употреблять выражение «случайный компонент неопределенности».
|
en uncertainty
fr incertitude
|
|
|
|
4.1. выборочная единица
а) Одна из конкретных единиц, из которых состоит
генеральная совокупность.
b) Определенное количество продукции, материала
или услуг, образующее единство и взятое из одного места, в одно время для
формирования части выборки.
Примечания
1.
Выборочная единица может содержать более одного изделия, допускающего
испытание, например пачка сигарет, но при этом получают один результат
испытания или наблюдения.
2. Единицей продукции может быть одно изделие,
пара или набор изделий, или ею может быть определенное количество материала,
такое как отрезок латунного прутка определенной длины, определенный объем
жидкой краски или заданная масса угля. Она необязательно должна быть такой
же, как единица закупки, поставки, производства или отгрузки.
|
en sampling unit
fr unite d’echantillonnage
|
|
4.2. выборка [проба]
Одна или несколько выборочных единиц, взятых из
генеральной совокупности и предназначенных для получения информации о ней.
Примечание - Выборка [проба] может служить основой для
принятия решения о генеральной совокупности или о процессе, который ее
формирует.
|
en sample
fr echantillon
|
|
4.3. объем выборки
Число выборочных единиц в выборке.
|
en sample size
fr effectif d’echantillon
|
|
4.4. отбор выборки
Процесс извлечения или составления выборки.
|
en sampling
fr echantillonnage
|
|
4.5. процедура выборочного контроля
Пооперационные требования и (или) инструкции,
связанные с реализацией конкретного плана выборочного контроля, то есть
запланированный метод отбора, извлечения и подготовки выборки (выборок) из
партий для получения информации о признаке (признаках) в партии.
|
en sampling procedure
fr procedure d’echantillonnage
|
|
4.6. выборка с возвращением
Выборка, из которой каждую отобранную и
наблюдаемую единицу возвращают в совокупность перед отбором следующей
единицы.
Примечание - Одна и та же единица может многократно
появляться в выборке.
|
en sampling with replacement
fr echantillonnage avec remise; echantillonnage non exhaustif
|
|
4.7. выборка без возвращения
Выборка, в которую единицы отбирают из
совокупности только один раз или последовательно и не возвращают в нее.
|
en sampling without replacement
fr echantillonnage sans remise; echantillonnage exhaustif
|
|
4.8. случайная выборка
Выборка n выборочных
единиц, взятых из совокупности таким образом, что каждая возможная комбинация
из n единиц имеет определенную
вероятность быть отобранной.
|
en random sample
fr echantillon au hasard
|
|
4.9. простая случайная выборка
Выборка n выборочных
единиц, взятых из совокупности таким образом, что все возможные комбинации из
n единиц имеют одинаковую вероятность быть
отобранными.
|
en simple random sample
fr echantillon simple au hasard
|
|
4.10. подвыборка
Выборка [проба], взятая из выборки [пробы] генеральной
совокупности.
Примечания
1. Ее
можно отбирать тем же методом, что и при отборе исходной выборки [пробы], но
это необязательно.
2. При отборе пробы из нештучной продукции
подвыборки часто получают делением пробы.
|
en subsample
fr sous-echantillon
|
|
4.11. деление пробы
Процесс отбора одной или нескольких проб из
пробы нештучной продукции таким способом, как нарезание, механическое деление
или квартование.
|
en sample division
fr division d’un echantillon
|
|
4.12. дублирующая выборка [проба]
Одна из двух или более выборок [проб] или
подвыборок [проб], полученных одновременно, одним методом ее отбора или
делением выборки [пробы].
|
en duplicate sample
fr echantillon dedouble
|
|
4.13. расслоение
Разделение совокупности на взаимоисключающие и исчерпывающие
подсовокупности, называемые слоями, которые должны быть более однородными
относительно исследуемых показателей, чем вся совокупность.
|
en stratification
fr stratification
|
|
4.14. расслоенная выборка [проба]
В совокупности, которую можно разделить на
различные взаимно исключающие и исчерпывающие подсовокупности, называемые
слоями, отбор, проводимый таким образом, что в выборку [пробу] отбирают
определенные доли от разных слоев и каждый слой представляют хотя бы одной
выборочной единицей.
|
en stratified sampling
fr echantillonnage stratifie
|
|
4.15. систематический отбор
Отбор выборки каким-либо систематическим
методом.
|
en systematic sampling
fr echantillonnage systematique
|
|
4.16. периодический систематический отбор
Отбор n выборочных
единиц с порядковыми номерами:
h, h + k,
h + 2k, ..., h + (n - 1) k,
где h и k - целые числа,
удовлетворяющие соотношениям
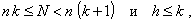
и h обычно выбирают случайно из k
первых целых чисел, если N объектов совокупности
расположены по определенной системе и если они пронумерованы от 1 до N.
Примечание - Периодический систематический отбор обычно
применяют для получения выборки, которая случайна по отношению к некоторым
признакам, о которых известно, что они не зависят от систематического
смещения.
|
en periodic systematic sampling
fr echantillonnage systematique periodique
|
|
4.17. период отбора (выборки)
Интервал времени, в течение которого берут
очередную выборочную единицу при периодическом систематическом отборе.
Примечание - Период отбора может быть постоянным или
зависеть от выхода или от скорости процесса, то есть зависеть от количества
материала, изготовленного в производственном процессе или загруженного в
процессе погрузки.
|
en sampling interval
fr intervalle d’echantillonnage
|
|
4.18. кластерный отбор; отбор методом
группировки
Способ отбора, при котором совокупность
разделяют на взаимоисключающие и исчерпывающие группы или кластеры, в которых
выборочные единицы объединены определенным образом, и выборку из этих
кластеров берут случайно, причем все выборочные единицы включают в общую
выборку.
|
en cluster sampling
fr ehantillonnage en grappe
|
|
4.19. многостадийный отбор
Отбор, при котором выборку берут в несколько
стадий, выборочные единицы на каждой стадии отбирают из больших выборочных
единиц, отобранных на предыдущей стадии.
|
en multi-stage sampling; nested sampling
fr echantillonnage a plusieurs degres; echantillonnage en serie
|
|
4.20. многостадийный кластерный отбор
Кластерный отбор, проведенный в две или более
стадии, при котором каждый отбор делают из кластеров, которые уже получены из
разделения предшествующей выборки.
|
en multi-stage cluster sampling
fr echantillonnage en grappe a plusieurs degres
|
|
4.21. первичная выборка [проба]
Выборка [проба], получаемая из совокупности на
первой стадии многостадийного отбора
|
en primary sample
fr echantillonnage primaire
|
|
4.22. вторичная выборка [проба]
Выборка [проба], получаемая из первичной выборки
[пробы] на второй стадии многостадийного отбора.
Примечание - Это можно распространить на k-ю
стадию при k > 2.
|
en secondary sample
fr echantillon secondaire
|
|
4.23. конечная выборка
Выборка, получаемая на последней стадии
многостадийного отбора.
|
en final sample
fr echantillon final
|
|
4.24. выборочная доля
а) Отношение объема выборки к общему числу
выборочных единиц.
b) Когда отбирают нештучную или непрерывно
производимую продукцию, выборочную долю определяют отношением количества
пробы к количеству совокупности или подсовокупности.
Примечание - Под количеством пробы или совокупности
понимают массу, объем, площадь и т.д.
|
en sampling fraction
fr taux d’echantillonnage; fraction de sondage
|
|
4.25. мгновенная проба
Количество нештучной продукции, взятое
единовременно за один прием из большего объема этой же продукции.
|
en increment
fr prelevement elementaire
|
|
4.26. образец (для испытаний)
Часть выборочной единицы, требуемая для целей
испытания.
|
en test piece
fr eprouvette
|
|
4.27. отбор проб
Отбор из партий нештучной продукции, где
выборочные единицы изначально трудноразличимы.
Примечание - Примерами могут служить отбор проб из больших
куч угля для анализа на содержание золы или теплоты сгорания, или табака на
содержание влаги.
|
en bulk sampling
fr echantillonnage en vrac
|
|
4.28. суммарная проба
Объединение мгновенных проб материала, когда
отбирают нештучную продукцию.
|
en aggregated sample
fr echantillon d’ensemble
|
|
4.29. объединенная выборка [проба]
Выборка [проба] из совокупности, получаемая
объединением всех выборочных единиц, взятых из этой совокупности.
|
en gross sample
fr echantillon global
|
|
4.30. подготовка пробы
Для нештучной продукции - система операций,
таких как измельчение, смешивание, деление и т.д., необходимых для
превращения отобранной пробы материала в лабораторную пробу или пробу для
испытаний.
Примечание - Подготовка пробы не должна, насколько это
возможно, изменять репрезентативность совокупности, из которой она
изготовлена.
|
en sample preparation
fr preparation d’un echantillon
|
|
4.31. лабораторная проба
Проба, предназначенная для лабораторных
исследований или испытаний.
|
en laboratory sample
fr echantillon pour laboratoire
|
|
4.32. проба для анализа
Проба, подготовленная для проведения испытаний
или анализа, которую полностью и единовременно используют для проведения
испытания или анализа.
|
en test sample; analysis sample
fr echantillon pour essai; echantillon pour analyse
|
|
|
|
c2-критерий 2.86
F-критерий 2.88
F-распределение 1.41
t-критерий 2.87
t-распределение 1.40
бета-распределение 1.45
величина (измеримая) 3.1
величина измеряемая 3.5
величина стандартизованная случайная 1.25
величина случайная 1.2
величина центрированная случайная 1.21
величина физическая 3.1
вероятность 1.1
вероятность доверительная 2.59
вероятность ошибки второго рода 2.78
вероятность ошибки первого рода 2.76
воспроизводимость (результатов проверки) 3.20
выборка 4.2
выборка без возвращения 4.7
выборка (проба) вторичная 4.22
выборка дублирующая 4.12
выборка конечная 4.23
выборка объединенная 4.28
выборка первичная 4.21
выборка расслоенная 4.14
выборка простая случайная 4.9
выборка с возвращением 4.6
выборка случайная 4.8
выбросы 2.64
гамма-распределение 1.44
гипотеза нулевая и гипотеза альтернативная 2.66
гипотеза простая 2.67
гипотеза сложная 2.68
гистограмма 2.17
граница доверительная 2.60
границы класса 2.8
границы толерантные 2.62
деление пробы 4.11
диаграмма разброса 2.21
диаграмма рассеяния 2.21
диаграмма столбиковая 2.18
дисперсия выборочная 2.33
дисперсия (случайной величины) 1.22
доля выборочная 4.24
единица 2.1
единица выборочная 4.1
значение (величины) истинное 3.2
значение (величины) действительное 3.3
значение критическое 2.72
значение наблюдаемое 2.6, 3.6
значение нормальное принятое 3.4
значение оценки 2.51
интервал двусторонний доверительный 2.57
интервал класса 2.10
интервал односторонний доверительный 2.58
интервал толерантный 2.61
квантиль (случайной величины) 1.14
квартиль 1.16
класс 2.7
ковариация 1.32
ковариация выборочная 2.40
корреляция 1.13
коэффициент вариации выборочный 2.35
коэффициент вариации (случайной величины) 1.24
коэффициент корреляции 1.33
коэффициент корреляции выборочный 2.41
коэффициент регрессии выборочный 2.44
кривая мощности (критерия) 2.81
кривая оперативной характеристики 2.83
кривая ОХ 2.83
кривая регрессии (Y по X) 1.34
кривая регрессии (Y по Х для выборки) 2.42
критерий двусторонний 2.74
критерий односторонний 2.73
критерий свободный от распределения 2.69
критерий согласия распределения 2.63
критерий статистический 2.65
критерий Стьюдента 2.87
критерий Фишера 2.88
медиана 1.15
медиана выборочная 2.28
мода 1.17
момент корреляционный 1.32
момент порядков q и s относительно
точки (а, b) совместный 1.30
момент порядков q и s совместный центральный 1.31
момент порядков q и s совместный
центральный выборочный 2.39
момент порядка q относительно a 1.27
момент порядка q относительно начала
отсчета 1.26
момент порядка q относительно начала
отсчета выборочный 2.36
момент порядка q центральный 1.28
момент порядка q центральный выборочный 2.37
момент порядков q и s относительно
начала отсчета совместный 1.29
момент порядков q и s относительно
начала отсчета совместный выборочный 2.38
момент порядков q и s совместный
центральный 1.31
момент порядков q и s совместный центральный
выборочный 2.39
мощность критерия 2.79
независимость (случайных величин) 1.11
неопределенность (результата проверки) 3.25
область критическая 2.71
образец (для испытаний) 4.26
объект 2.1
объем выборки 4.3
ожидание (случайной величины) математическое 1.18
ожидание маргинальное математическое 1.19
ожидание условное математическое 1.20
отбор выборки 4.4
отбор проб 4.27
отбор кластерный 4.18
отбор методом группировки 4.18
отбор многостадийный 4.19
отбор кластерный многостадийный 4.20
отбор периодический систематический 4.16
отбор систематический 4.15
отклонение (случайной величины) стандартное 1.23
отклонение воспроизводимости стандартное 3.22
отклонение повторяемости стандартное 3.17
отклонение (выборки) среднее 2.32
отклонение стандартное выборочное 2.34
отклонение стандартное относительное 2.35
оценивание (параметра) 2.49
оценка 2.50
оценка несмещенная 2.55
ошибка второго рода 2.77
ошибка первого рода 2.75
ошибка результата (проверки) 3.8
ошибка результата (проверки) систематическая 3.10
ошибка результата (проверки) случайная 3.9
ошибка среднеквадратичная 2.56
ошибка стандартная 2.56
параметр 1.12
период отбора (выборки) 4.17
плотность распределения (вероятностей) 1.5
поверхность регрессии (Z по Х и Y) 1.35
поверхность регрессии (Z по X и Y для выборки) 2.43
повторение 2.89
повторяемость (результата проверки) 3.15
погрешность выборочного метода 2.53
погрешность оценки 2.52
подвыборка 4.10
подготовка пробы 4.30
подсовокупность 2.5
полигон кумулятивных частот 2.19
правильность (результата проверки) 3.12
предел воспроизводимости 3.23
предел повторяемости 3.18
пределы класса 2.8
прецизионность (результата проверки) 3.14
признак 2.2
причины случайные 2.92
проба 4.2
проба вторичная 4.22
проба для анализа 4.32
проба дублирующая 4.12
проба лабораторная 4.31
проба мгновенная 4 25
проба первичная 4.21
проба объединенная 4.29
проба суммарная 4.28
проба расслоенная 4.14
проведение эксперимента повторное 2.90
процедура выборочного контроля 4.5
размах (выборки) 2.30
размах (выборок) средний 2.31
разность воспроизводимости критическая 3.24
разность повторяемости критическая 3.19
рамки отбора 2.4
рандомизация 2.91
распределение c2 1.39
распределение биномиальное 1.49
распределение Вейбулла 1.48
распределение (вероятностей) маргинальное 1.9
распределение (вероятностей) 1.3
распределение (вероятностей) условное 1.10
распределение гипергеометрическое 1.52
распределение Гумбеля 1.46
распределение двумерное нормальное 1.53
распределение двумерное Лапласа- Гаусса 1.53
распределение двумерное Лапласа- Гаусса
нормированное 1.54
распределение Лапласа-Гаусса 1.37
распределение Лапласа- Гаусса стандартное 1.38
распределение логарифмически нормальное 1.42
распределение многомерной случайной величины 1.55
распределение мультиномиальное 1.55
распределение нормальное 1.37
распределение стандартизованное двумерное
нормальное 1.54
распределение стандартное нормальное 1.38
распределение Стьюдента 1.40
распределение отрицательное биномиальное 1.50
распределение прямоугольное 1.36
распределение Пуассона 1.51
распределение равномерное 1.36
распределение Фрешэ 1.47
распределение частот 2.15
распределение частот двумерное 2.20
распределение частот маргинальное 2.24
распределение частот многомерное 2.23
распределение частот одномерное 2.16
распределение частот условное 2.25
распределение экспоненциальное 1.43
распределение экстремальных значений типа I 1.46
распределение экстремальных значений типа II 1.47
распределение экстремальных значений типа III 1.48
расслоение 4.13
результат (на выбранном уровне значимости a) значимый 2.84
результат проверки 3.7
реплика 2.90
середина класса 2.9
середина размаха (выборки) 2.29
серия 2.48
смещение (результата проверки) 3.13
смещение оценки 2.54
совокупность (генеральная) 2.3
среднее арифметическое 2.26
среднее арифметическое взвешенное 2.27
статистика 2.45
статистика порядковая 2.46
степень свободы 2.85
сходимость 3.15
таблица сопряженности двух признаков 2.22
точность (результата проверки) 3.11
тренд 2.47
уровень доверия 2.59
уровень значимости (критерия) 2.70
условия воспроизводимости 3.21
условия повторяемости 3.16
функция мощности критерия 2.80
функция распределения 1.4
функция распределения (вероятностей) масс 1.6
функция распределения двумерная 1.7
функция распределения многомерная 1.8
характеристика оперативная 2.82
частота 2.11
частота кумулятивная относительная 2.14
частота накопленная кумулятивная 2.12
частота относительная 2.13
c2-distribution 1.39
c2-test 2.86
accepted reference value 3.4
accuracy 3.11
aggregated sample 4.28
alternative hypothesis 2.66
analysis sample 4.32
arithmetic mean 2.26
arithmetic weighted mean 2.27
average 2.26
average range 2.31
bar chart 2.18
bar diagram 2.18
beta distribution 1.45
bias 3.13
bias of estimator 2.54
binomial distribution 1.49
bivariate distribution function 1.7
bivariate frequency distribution 2.20
bivariate Laplace - Gauss distribution 1.53
bivariate normal distribution 1.53
bulk sampling 4.27
cell 2.7
central moment of order q 1.28
central moment of order q, sample 2.37
centered random variable 1.21
chance causes 2.92
characteristic 2.2
chi-squared distribution 1.39
chi-squared test 2.86
class 2.7
class boundaries 2.8
class limits 2.8
class width 2.10
cluster sampling 4.18
coefficient of variation 1.24
coefficient of variation, sample 2.35
composite hypothesis 2.68
conditional expectation 1.20
conditional frequency distribution 2.25
conditional probability distribution 1.10
confidence coefficient 2.59
confidence level 2.59
confidence limit 2.60
contingency table 2.22
conventional true value (of a quantity) 3.3
correlation 1.13
correlation coefficient 1.33
correlation coefficient, sample 2.41
covariance 1.32
covariance, sample 1.32
critical region 2.71
critical value 2.72
cumulative frequency 2.12
cumulative frequency polygon 2.19
cumulative relative frequency 2.14
degree of freedom 2.85
distribution free-test 2.69
distribution function 1.4
duplicate sample 4.12
entity 2.1
error of result 3.8
error of the first kind 2.75
error of the second kind 2.77
estimate 2.51
estimation 2.49
estimator 2.50
estimator error 2.52
expectation 1.18
expected value 1.18
exponential distribution 1.43
F-distribution 1.41
final sample 4.23
Frechet distribution 1.47
frequency 2.11
frequency distribution 2.15
F-test 2.88
gamma distribution 1.44
goodness of fit of a distribution 2.63
gross sample 4.29
Gumbel distribution 1.46
histogram 2.17
hypergeometric distribution 1.52
increment 4.25
independence 1.11
item 2.1
joint central moment of orders q and s 1.31
joint central moment of orders q and s, sample 2.39
joint moment of orders q and s about an origin (a,
b) 1.30
joint moment of orders q and s about the origin 1.29
joint moment of orders q and s about the origin, sample 2.38
laboratory sample 4.31
Laplace - Gauss distribution 1.37
log-normal distribution 1.42
marginal expectation 1.19
marginal frequency distribution 2.24
marginal probability distribution 1.9
mean 1.18
mean deviation 2.32
mean range 2.31
measurand 3.5
(measurable) quantity 3.1
median 1.15
median, sample 2.28
mid-point of class 2.9
mid-range 2.29
mode 1.17
moment of order q about an origin a 1.27
moment of order q about the origin 1.26
moment of order q about the origin, sample 2.36
multinomial distribution 1.55
multi-stage cluster sampling 4.20
multi-stage sampling 4.19
multivariate distribution function 1.8
multivariate frequency distribution 2.23
negative binomial distribution 1.50
nested sampling 4.19
normal distribution 1.37
null hypothesis 2.66
observed value 2.6, 3.6
one-sided confidence interval 2.58
one-sided test 2.73
operating characteristic 2.82
operating characteristic curve 2.83
order statistics 2.46
outliers 2.64
parameter 1.12
periodic systematic sampling 4.16
Poisson distribution 1.51
population 2.3
power curve 2.81
power function of a test 2.80
power of a test 2.79
precision 3.14
primary sample 4.21
probability 1.1
probability density function 1.5
probability distribution 1.3
probability mass function 1.6
quantile 1.14
quantity (measurable) 3.1
quartile 1.16
random error of result 3.9
random sample 4.8
random variable 1.2
randomization 2.91
range 2.30
rectangular distribution 1.36
regression coefficient, sample 2.44
regression curve 1.34, 2.42
regression surface 1.35, 2.43
relative frequency 2.13
repeatability 3.15
repeatability conditions 3.16
repeatability critical difference 3.19
repeatability limit 3.18
repeatability standard deviation 3.17
repetition 2.89
replication 2.90
reproducibility 3.20
reproducibility conditions 3.21
reproducibility critical difference 3.24
reproducibility limit 3.23
reproducibility standard deviation 3.22
run 2.48
sample 4.2
sample division 4.11
sample preparation 4.30
sample size 4.3
sampling 4.4
sampling error 2.53
sampling fraction 4.24
sampling frame 2.4
sampling interval 4.17
sampling procedure 4.5
sampling unit 4.1
sampling with replacement 4.6
sampling without replacement 4.7
scatter diagram 2.21
secondary sample 4.22
significance level 2.70
significant result (at the closen significance level a) 2.84
simple hypothesis 2.67
simple random sample 4.9
standard deviation 1.23
standard, sampling 2.34
standard error 2.56
standardized bivariate Laplace-Gauss distribution 1.54
standardized bivariate normal distribution 1.54
standardized Laplace-Gauss distribution 1.38
standardized normal distribution 1.38
standardized random variable 1.25
statistical coverage interval 2.61
statistical coverage limits 2.62
statistical test 2.65
statistics 2.45
stratification 4.13
stratified sampling 4.14
Students distribution 1.40
Students test 2.87
subpopuiation 2.5
subsample 4.10
systematic error of result 3.10
systematic sampling 4.15
t-distribirtion 1.40
t-test 2.87
test piece 4.26
test result 3.7
test sample 4.32
trend 2.47
true value (of a quantity) 3.2
trueness 3.12
two-sided confidence interval 2.57
two-sided test 2.74
two-way table of frequencies 2.22
type I error probability 2.76
type I extreme value distribution 1.46
type II error probability 2.78
type II extreme value distribution 1.47
type III extreme value distribution 1.48
unbiased estimator 2.55
uncertainty 3.25
uniform distribution 1.36
univariate frequency distribution 2.16
variance 1.22
variance, sampling 2.33
variate 1.2
Weibull distribution 1.48
weighted average 2.27
abequation d’une distribution 2.63
base d’echantillonnage 2.4
biais 3.13
biais d’un estimateur 2.54
caractere 2.2
causes aleatoires 2.92
centre de classe 2.9
classe 2.7
classe, largeur de 2.10
coefficient de correlation 1.33, 2.41
coefficient de regression 2.44
coefficient de variation 1.24, 2.35
conditions de repetabilite 3.16
conditions de reproductibilite 3.21
correlation 1.13
courbe d’efficacite 2.83
courbe de puissance 2.81
courbe de regression 1.34, 2.42
covariance 1.32, 2.40
degre de liberte 2.85
diagramme en batons 2.18
difference critique de repetabilite 3.19
difference critique de reproductibilite 3.24
distribution d’effectif 2.15
distribution d’effectif a deux variables 2.20
distribution d’effectif a plusieurs variables 2.23
distribution d’effectif a une variable 2.16
distribution d’effectif conditionnelle 2.25
distribution d’effectif marginale 2.24
division d’un echantillon 4.11
ecart moyen 2.32
ecart-type 1.23, 2.34
ecart-type de repetabilite 3.17
ecart-type de reproductibilite 3.22
echantillon 4.2
echantillon au hasard 4.8
echantillon dedouble 4.12
echantillon d’ensemble 4.28
echantillon final 4.23
echantillon global 4.29
echantillon pour analyse 4.32
echantillon pour essai 4.32
echantillon pour laboratoire 4.31
echantillon secondaire 4.22
echantillon simple au hasard 4.9
echantillonnage 4.4
echantillonnage a plusieurs degrees 4.19
echantillonnage avec remise 4.6
echantillonnage en grappe a plusieurs degrees 4.20
echantillonnage en grappe 4.18
echantillonnage en serie 4.19
echantillonnage en vrac 4.27
echantillonnage exhaustif 4.7
echantillonnage non exhaustif 4.6
echantillonnage primaire 4.21
echantillonnage sans remise 4.7
echantillonnage stratifie 4.14
echantillonnage systematique 4.15
echantillonnage systematique periodique 4.16
effectif 2.11
effectif cumule 2.12
effectif d’echantillon 4.3
efficacite 2.82
entite 2.1
eprouvette 4.26
erreur aleatoire de resultat 3.9
erreur d’echantillonnage 2.53
erreur de premiere espece 2.75
erreur de resultat 3.8
erreur d’estimation 2.52
erreur de seconde espece 2.77
erreur systematique de resultat 3.10
erreur-type 2.56
esperance mathematique 1.18
esperance mathematique conditionnelle 1.20
esperance mathematique marginale 1.19
estimateur 2.50
estimateur sans biais 2.55
estimation 2.49
estimation (resultat) 2.51
etendue 2.30
etendue moyenne 2.31
exactitude 3.11
fidelite 3.14
fonction d’efficacite d’un test 2.82
fonction de densite de probabilite 1.5
fonction de masse 1.6
fonction de puissance d’un test 2.80
fonction de repartition 1.4
fonction de repartition a deux variables 1.7
fonction de repartition a plusieurs variables 1.8
fraction de sondage 4.24
frequence 2.13
frequence cumulee 2.14
frontieres de classe 2.8
grandeur (mesurable) 3.1
histogramme 2.17
hypergeometrique, loi 1.52
hypothese alternative 2.66
hypothese composite 2.68
hypothese nulle 2.66
hypothese simple 2.67
incertitude 3.25
independance 1.11
individu 2.1
intervalle d’echantillonnage 4.17
intervalle de confiance bilateral 2.57
intervalle de confiance unilateral 2.58
intervalle statistique de dispersion 2.61
justesse 3.12
Laplace - Gauss, loi de 1.37
Laplace - Gauss a deux variables, loi de 1.53
Laplace - Gauss reduite, loi de 1.38
Laplace - Gauss reduite a deux variables, loi de 1.54
largeur de classe 2.10
limite de confiance 2.60
limite de repetabilite 3.18
limite de reproductibilite 3.23
limites de classe 2.8
limites statistiques de dispersion 2.62
loi beta 1.45
loi binomiale 1.49
loi binomiale negative 1.50
loi de chi carre 1.39
loi de F 1.41
loi de Frechet 1.47
loi de Gumbel 1.46
loi de c2 1.39
loi de Laplace - Gauss 1.37
loi de Laplace - Gauss a deux variables 1.53
loi de Laplace - Gauss reduite 1.38
loi de Laplace - Gauss reduite a deux variables 1.54
loi de Poisson 1.51
loi de probabilite conditionnelle 1.10
loi de probabilite 1.3
loi de probabilite marginale 1.9
loi des valeurs extremes de type I 1.46
loi des valeurs extremes de type II 1.47
loi des valeurs extremes de type III 1.48
loi de Student 1.40
loi de t 1.40
loi de Weibull 1.48
loi exponentielle 1.43
loi gamma 1.44
loi hypergeometrique 1.52
loi log-normale 1.42
loi multinomiale 1.55
loi normale 1.37
loi normale a deux variables 1.53
loi normale reduite 1.38
loi normale reduite a deux variables 1.54
loi rectangulaire 1.36
loi uniforme 1.36
mediane 1.15, 2.28
mesurande 3.5
milieu de 1etendue 2.29
mode 1.17
moment centre d’ordre q 1.28, 2.37
moment centre d’ordres q et s 1.31, 2.39
moment d’ordre q par rapport a l’origine 1.26, 2.36
moment d’ordres q et s a partir de l’origine 1.29, 2.38
moment d’ordre q a partir d’une origine a 1.27
moment d’ordres q et s a partir d’une origine (a,
b) 1.30
moyenne 1.18, 2.26
moyenne arithmetique 2.26
moyenne arithmetique ponderee 2.27
moyenne ponderee 2.27
niveau de confiance 2.59
niveau de signification 2.70
nuage de points 2.21
parametre 1.12
polygone d’effectif cumule 2.19
population 2.3
prelevement elementaire 4.25
preparation d’un echantillon 4.30
procedure d’echantillonnage 4.5
probabilite 1.1
probabilite d’erreur de premiere espece 2.76
probabilite d’erreur de seconde espece 2.78
puissance d’un test 2.79
quantile 1.14
quartile 1.16
randomisation 2.91
region critique 2.71
repetabilite 3.15
repetition 2.89
replique 2.90
reproductibilite 3.20
resultat dessai 3.7
resultat significatif (au niveau de signification a choisi) 2.84
sous-echantillon 4.10
sous-population 2.5
statistique 2.45
statistique d’ordre 2.46
stratification 4.13
suite 2.48
surface de regression 1.35, 2.43
table d’effectif a double entree 2.22
tableau de contingence 2.22
taux d’echantillonnage 4.24
tendance 2.47
test bilateral 2.74
test de chi carre 2.86
test de Student 2.87
test F 2.88
test c2 2.86
test non parametrique 2.69
test statistique 2.65
test t 2.87
test unilateral 2.73
unite d’echantillonnage 4.1
valeur conventionnellement vraie 3.3
valeur critique 2.72
valeur de reference acceptee 3.4
valeur esperee 1.18
valeur observee 2.6, 3.6
valeur vraie (d’une grandeur) 3.2
valeurs aberrantes 2.64
valeurs extremes de type I, loi de 1.46
valeurs extremes de type II, loi de 1.47
valeurs extremes de type III, loi de 1.48
validite de l’ajustement 2.63
variable aleatoire 1.2
variable aleatoire centree 1.21
variable aleatoire centree reduite 1.25
variance 2.33
variance 1.22
(справочное)
БИБЛИОГРАФИЯ
[1] Международный словарь основных и общих
терминов метрологии. - ISO/IEC/OIML/BIPM. - Женева, 1984.
[2] МИ 2247-93 Рекомендация. Государственная
система обеспечения единства измерений. Метрология. Основные термины и
определения. - С.-Пб.: ВНИИМ им. Д. И. Менделеева, 1994.
Ключевые слова: теория вероятностей, распределение
случайной величины, статистика, случайная выборка, среднее, дисперсия,
точность, правильность, прецизионность