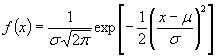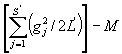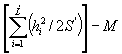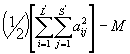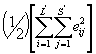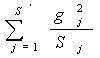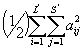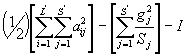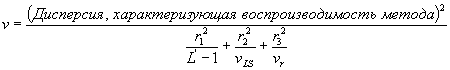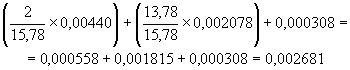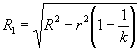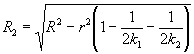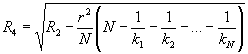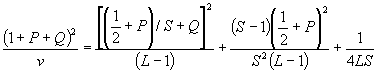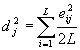
Полное меню
- Актуальное
законодательство - Интернет
и право- - Рассылка ''Закон есть закон''
- - Форум сайта (архив)
- - Законодательство
- - Судебная практика (необычная)
- - Судебная практика (авторская)
- - Процедура UDRP и и решения WIPO
- - Книги серии ''Интернет и Право''
- - Книги в открытом доступе
- - Учебный курс ''Интернет и Право''
- - Учебный курс ''Доменные споры''
- - Литература по ''Интернет и Право''
- - Литература по интел. собственности
- - Научный уголок (работы гостей)
- - Авторские публикации
- Информационные
материалы - ЮРИДИЧЕСКИЕ
УСЛУГИ- - Перечень юридических услуг
- - Карта юридических услуг
- - Юридическая консультация
- - Доменные споры (RU), авторское право
- - Международный суд по доменам (COM)
- - Защита прав на маркетплейсе (WB, Ozon)
- - Защита прав в соцсетях (Vk, Ok, FB)
- - Купля-продажа домена, сайта, ПО
- - Досудебное урегулирование конфликта
- - Защита чести и деловой репутации
- - Отмена блокировки сайта/домена РКН
- - ФАС: товарные знаки, авторское право
- - Регистрация ПО/сайта (Роспатент)
- - Юридическая проверка домена
- - Нотариальное заверение сайтов
- - Способы и формы оплаты услуг
- - Мы в СМИ
- - О компании, клиенты
- - Наши дела и победы
- - Контакты и реквизиты
- Информация
о сайте -




Основные ссылки |
Вернуться в "Каталог СНиП"ГОСТ Р 8.580-2001* ГСИ. Определение и применение показателей прецизионности методов испытаний нефтепродуктов.ГОСТ Р 8.580-2001 ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННАЯ СИСТЕМА Определение
и применение показателей ПРЕЦИЗИОННОСТИ ГОССТАНДАРТ РОССИИ Москва Предисловие 1 РАЗРАБОТАН Всероссийским научно-исследовательским институтом по переработке нефти (ОАО «ВНИИ НП»), Уральским научно-исследовательским институтом метрологии (УНИИМ) ВНЕСЕН Управлением метрологии Госстандарта России 2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 7 июля 2001 г. № 224-ст 3 Стандарт разработан на основе международного стандарта ИСО 4259-92 Petroleum Products. Determination and application of precision data in relation to methods of test, который распространяется на определение и применение показателей прецизионности (повторяемости и воспроизводимости) методов испытаний нефти и нефтепродуктов. Показатели прецизионности зависят только от случайных факторов и не связаны с истинным или условно истинным значением (см. 3.14 ИСО 3534-1, ИСО 5725-1). Измененная редакция. Изм. № 1. 4 ВВЕДЕН ВПЕРВЫЕ СОДЕРЖАНИЕ Введение Свойства товарных нефти и нефтепродуктов оценивают с помощью стандартных лабораторных методов испытаний для контроля качества и проверки соответствия требованиям спецификаций. Два или более измерений одного и того же свойства определенного образца, выполненные каким-либо методом испытаний, обычно не дают точно один и тот же результат. Поэтому необходимо принять статистически обоснованные оценки показателей прецизионности методов введением объективной меры согласованности, которую ожидают для двух или более результатов, полученных в точно определенных условиях. Пояснения к некоторым понятиям, используемым в настоящем стандарте, приведены в приложении Л. Измененная редакция. Изм. № 1. ГОСТ Р 8.580-2001 ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Дата введения 2002-01-01 Измененная редакция. Изм. № 1. 1 Область примененияНастоящий стандарт устанавливает способ определения и применение показателей прецизионности [повторяемости (сходимости) и воспроизводимости]* методов испытаний нефти и нефтепродуктов (далее - нефтепродуктов). * См. приложение Л. Стандарт не распространяется на материалы и вещества неоднородного состава. Измененная редакция. Изм. № 1. 1а Нормативные ссылкиВ настоящем стандарте использованы ссылки на следующие стандарты: ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике Раздел 1а введен дополнительно. Изм. № 1. 2 ОпределенияВ настоящем стандарте применяют следующие термины с соответствующими определениями, отдельные определения даны в соответствии с ГОСТ Р ИСО 5725-1, [1] и [2]: Измененная редакция. Изм. № 1. 2.1 дисперсионный анализ: Метод анализа, позволяющий разложить общую дисперсию результатов испытаний, присущую данному методу, на составляющие, обусловленные действием определенных факторов. 2.2 межлабораторная (лабораторная) дисперсия: Рассеяние результатов, полученных более чем в одной лаборатории, которое обычно больше, чем в случае проведения того же числа испытаний в одной лаборатории. Примечание - Термин используют при классификации представительных параметров дисперсии генеральной совокупности результатов, например «лабораторная дисперсия». 2.3 смещение (отклонение): Разность между математическим ожиданием результатов испытаний и известным значением, если его можно определить. Примечания 1 Для целей данного стандарта математическое ожидание (среднее значение заданной совокупности результатов испытаний) выполняет роль «истинного значения или опорного значения» (см. 2.24) (ГОСТ Р ИСО 5725-1, 3.5, d). 2 Для целей данного стандарта «известное значение» по 2.8. Измененная редакция. Изм. № 1. 2.4 кодирование проб: Присвоение различным пробам определенных неповторяющихся номеров, при этом оператор не должен иметь другой идентификации или информации о пробах. 2.5 контрольная проба (проба для испытания): Проба, отобранная в месте передачи продукта, т.е. в месте, где ответственность за качество продукта переходит от поставщика к получателю. 2.6 число степеней свободы: Делитель, используемый в расчете дисперсии (число, которое на единицу меньше числа независимых результатов). Примечание - Данное определение применимо только к простейшим случаям. Исчерпывающие определения выходят за область данного стандарта. 2.7 определение: Процесс выполнения серии операций, регламентированных в документе на метод испытаний, в результате выполнения которых получают единичное значение. 2.8 известное значение: Действительное количественное значение величины, установленное процедурой приготовления. Примечание - Известное значение существует не всегда. Оно не может быть определено для эмпирических условных величин (например температуры вспышки). 2.9 среднее значение (среднеарифметическое значение, среднее): Сумма результатов для данного ряда, деленная на их число. 2.10 средний квадрат: Сумма квадратов, деленная на число степеней свободы. 2.11 нормальное распределение: Распределение вероятностей случайной непрерывной величины X, если х - любое действительное число, при котором плотность вероятности составляет
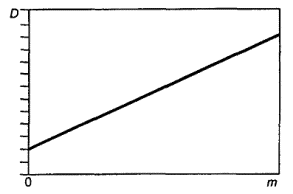
где m - истинное значение, s - среднеквадратическое отклонение для нормального распределения (s > 0). 2.12 оператор: Лицо, выполняющее операции испытаний. 2.13 выброс: Элемент совокупности значений, который несовместим с остальными элементами данной совокупности (см. ГОСТ Р ИСО 5725-1). Примечание – Статистические критерии (меры и уровни значимости), используемые для идентификации выбросов в экспериментах по оценке прецизионности на основе исследований результатов межлабораторных испытаний, изложены в разделе 4 настоящего стандарта. Измененная редакция. Изм. № 1. 2.14 прецизионность: Степень близости друг к другу независимых результатов испытаний, полученных в конкретных регламентированных условиях (см. ГОСТ Р ИСО 5725-1 и [2]). Примечание – «Независимые результаты испытаний» – результаты, полученные способом, на который не оказывает влияния никакой предшествующий результат, полученный при испытаниях того же самого или подобного объекта. Количественные значения мер прецизионности существенно зависят от регламентированных условий. Крайними случаями таких условий являются условия повторяемости и условия воспроизводимости [2]. Измененная редакция. Изм. № 1. 2.15 Исключен. Изм. № 1. 2.16 получатель: Лицо или организация, которые получают или принимают поставляемый поставщиком продукт. 2.17 Повторяемость (сходимость) метода. 2.17.1 повторяемость результатов испытаний: Степень близости друг к другу независимых результатов испытаний, полученных одним и тем же методом на идентичном материале, в одной и той же лаборатории одним и тем же оператором, с использованием одного и того же оборудования в пределах короткого промежутка времени [2]. Примечание – Вероятными характеристиками (статистическими оценками), показателями повторяемости результатов испытаний являются среднеквадратическое отклонение результатов испытаний в условиях повторяемости, дисперсия в условиях повторяемости. Термин «повторяемость (сходимость) результатов испытаний» не следует смешивать с термином «повторное испытание» (в 2.18). Повторяемость (сходимость) относят к состоянию, когда случайная изменчивость результатов минимальна. Поэтому период времени, в течение которого получают повторные результаты, должен быть минимальным, чтобы исключить ошибки, зависящие от времени, например ошибки, связанные с влиянием окружающей среды и стабильностью градуировки. Измененная редакция. Изм. № 1. 2.17.2 предел повторяемости (сходимости) r: Абсолютное значение, разности двух единичных результатов испытаний, полученных в условиях повторяемости (см. 2.17.1) доверительной вероятностью 95 %. Измененная редакция. Изм. № 1. 2.18 повторное испытание: Многократное выполнение испытаний с соблюдением требований методики с целью повышения прецизионности результатов испытаний и получения меньшей ошибки испытаний. Повторное испытание следует отличать от обычного повторения, так как оно предполагает выполнение повторных испытаний (дублей) в одном месте и по возможности в одно и то же время. Повторным испытанием качественно определяют представительные характеристики дисперсии генеральной совокупности, которые могут быть связаны с повторными экспериментами при повторных испытаниях, например среднеквадратическое отклонение результатов для повторных испытаний. Измененная редакция. Изм. № 1. 2.19 Воспроизводимость метода 2.19.1 воспроизводимость результатов испытаний: Степень близости друг к другу независимых результатов испытаний, полученных одним и тем же методом на идентичном материале в разных лабораториях, разными операторами, с использованием различного оборудования [3]. Примечание - Вероятными характеристиками (статистическими оценками), показателями воспроизводимости результатов испытаний являются среднеквадратическое отклонение результатов испытаний в условиях воспроизводимости, дисперсия в условиях воспроизводимости. Измененная редакция. Изм. № 1. 2.19.2 предел воспроизводимости R: Абсолютное значение разности двух результатов испытаний в условиях воспроизводимости (см. 2.19.1) с доверительной вероятностью 95 %. Измененная редакция. Изм. № 1. 2.20 результат испытаний: Значение, полученное на одном или нескольких определениях в зависимости от требований, регламентированных в документе на метод испытаний (результат округляют в соответствии с приложением Ж). 2.21 среднеквадратическое отклонение: Мера рассеяния серий результатов испытаний относительно среднего значения равна положительному значению квадратного корня из дисперсии (оценивают по положительному значению квадратного корня из среднего квадрата). 2.22 сумма квадратов: Сумма квадратов разностей серий результатов и их среднего значения. 2.23 поставщик: Лицо или организация, которые отвечают за качество продукта вплоть до того момента, когда продукт принят получателем. 2.24 принятое опорное значение (для целей данного стандарта выполняет роль истинного значения): Значение, которое служит в качестве согласованного для сравнения с результатом испытаний и получено как математическое ожидание измеряемой характеристики, то есть среднее значение заданной совокупности результатов испытаний, полученных в лабораториях при условии, что n неограниченно возрастает (стремится к бесконечности). Истинное значение (принятое опорное значение) зависит от применяемого метода испытаний [2]. Измененная редакция. Изм. № 1. 2.25 дисперсия: Среднее значение квадратов отклонения случайной переменной от ее среднего, которое оценивают по среднему квадрату. 3 Программа межлабораторных испытаний для определения показателей прецизионности метода испытанийИзмененная редакция. Изм. № 1. 3.1 Планирование программы межлабораторных испытаний3.1.1 Планирование программы межлабораторных испытаний состоит из следующих этапов: а) подготовка проекта документа на метод испытаний; б) планирование программы пилотных испытаний с участием двух или более лабораторий; в) планирование программы межлабораторных испытаний. 3.1.2 Подготовка проекта документа на метод испытаний Документ должен содержать описание всех необходимых деталей выполнения испытаний и форму отчета о результатах испытания. Любое условие, которое может повлиять на результаты, должно быть регламентировано. Раздел, относящийся к показателям прецизионности, следует включать на этой стадии только в виде заглавия раздела. Измененная редакция. Изм. № 1. 3.1.3 Планирование программы пилотных испытаний с участием двух или более лабораторий 3.1.3.1 Программа пилотных испытаний необходима для: а) детальной проверки операций испытаний; б) выяснения возможности успешного выполнения оператором инструкций в документе на метод испытаний; в) контроля мер предосторожности при обращении с пробами; г) предварительной оценки показателей прецизионности результатов испытаний. Измененная редакция. Изм. № 1. 3.1.3.2 Для того, чтобы охватить диапазон определяемых значений результатов испытаний указанного метода, используют не менее двух проб. Следует включать не менее 12 комбинаций «лаборатория ´ проба». Каждую пробу испытывают дважды в каждой лаборатории в условиях повторяемости (сходимости). Если в проекте документа на метод выявляют какие-либо упущения или неточности, на этом этапе их следует исправить. Результаты следует анализировать с точки зрения их повторяемости (сходимости), воспроизводимости и наличия смещения. Если нарушение одного из этих условий слишком велико, следует рассмотреть необходимые изменения метода испытаний. 3.1.4 Планирование программы межлабораторных испытаний 3.1.4.1 Необходимо, чтобы в испытаниях участвовало пять или более лабораторий. Для уменьшения требуемого количества проб в испытаниях должны участвовать не менее шести лабораторий. Количество проб должно быть достаточным, чтобы охватить диапазон уровней измеряемого свойства и обеспечить надежность оценок показателей прецизионности. Если результаты пилотных испытаний обнаруживают какое-либо изменение показателей прецизионности в зависимости от уровня свойства, тогда в программе межлабораторных испытаний следует предусмотреть использование не менее пяти проб. В любом случае необходимо получить не менее 30 степеней свободы и для повторяемости (сходимости), и для воспроизводимости метода. Это означает, что при планировании программы следует добиваться того, чтобы для повторяемости (сходимости) общее число пар результатов было не менее 30. Измененная редакция. Изм. № 1. 3.1.4.2 Что касается воспроизводимости, то в приложении А минимальное число необходимых для испытаний проб приведено в зависимости от общего числа лабораторий - участников испытаний (L), отношений оценок составляющих (компонент) дисперсии (Р, Q), полученных в результате выполнения пилотной программы. При этом Р представляет отношение компоненты, обусловленной взаимодействием, к компоненте по дублям, а Q - отношение лабораторной компоненты к компоненте по дублям. В приложении Б приведены формулы, использованные при составлении таблицы A.1. Если Q много больше, чем Р, то невозможно получить 30 степеней свободы для дисперсии. Пропуски в таблице A.1 соответствуют этой или близкой к этой ситуациям (т.е. случаям, когда для испытаний необходимо более 20 проб). В этих случаях вероятны существенные расхождения между лабораториями. 3.2 Выполнение программы межлабораторных испытаний3.2.1 За выполнение всей программы испытаний, начиная с распространения документов и проб и кончая оцениванием результатов испытаний, должно быть ответственным одно лицо. Это лицо должно быть знакомо с методом испытаний, однако ему не следует лично принимать участие в испытаниях. Документ с описанием метода должен быть передан всем лабораториям заблаговременно. Если какой-либо лаборатории необходимо получить опыт выполнения операций метода заранее, то эту работу следует выполнять на других пробах, а не на тех, которые используют в рамках программы. 3.2.2 Пробы должны быть складированы, разделены на части, закодированы и распределены организатором испытаний, которому следует хранить резервное количество проб на случай непредвиденных обстоятельств. При этом важно, чтобы порции для отдельных лабораторий оставались однородными. При рассылке пробы должны быть снабжены следующими документами и инструкциями: а) согласованный проект документа на метод испытаний; б) инструкции по хранению проб и обращению с ними; в) порядок, в котором пробы необходимо испытывать (для каждой лаборатории случайный порядок различен); г) указание о том, что два результата должны быть получены на одной пробе последовательно одним оператором на одном комплекте оборудования. По статистическим причинам важно, чтобы два результата были получены независимо один от другого, т.е. чтобы знание первого результата не вызывало смещение второго результата. При невозможности исключения субъективности оператора необходимо получать пары результатов в режиме слепого кодирования, но таким образом, чтобы обеспечить выполнение испытаний в короткий интервал времени; д) период времени, в течение которого должны быть получены повторные результаты испытаний, и период времени, в течение которого должны быть испытаны все пробы; е) форма протокола для отчета о результатах испытаний. Для каждой пробы должно быть предусмотрено место для даты проведения испытаний, двух результатов и комментариев по любым необычным обстоятельствам. Специально следует указать число значащих цифр в отчете о результатах испытаний; ж) указание о том, что испытания должны быть выполнены в обычных условиях проведения испытаний с привлечением опытных операторов и продолжительность испытаний должна быть такой же, как при обычных испытаниях. Операторы, принимавшие участие в выполнении пилотной программы испытаний, могут принимать участие и в выполнении программы межлабораторных испытаний. Если их дополнительный опыт в проведении испытаний небольшого дополнительного числа проб оказывает заметное влияние, то это должно служить предупреждением о том, что исследуемый метод является неудовлетворительным. Для того, чтобы любой такой эффект можно было обнаружить, необходимо в отчете о результатах испытаний обеспечить возможность идентификации этих операторов. 4 Исследование результатов межлабораторных испытаний с целью проверки однородности и выявления выбросовПо результатам выполнения статистически обоснованной программы межлабораторных испытаний (раздел 3) устанавливают: а) зависимость или независимость показателей прецизионности от уровня результатов испытаний; б) однородность показателей прецизионности для всех лабораторий и присутствие выбросов (аномальных результатов). Технические приемы расчета результатов испытаний и примеры (расчет бромного числа) в обозначениях, указанных в приложении В, приведены в приложении Г. Предполагают, что все результаты получены из одной нормально распределенной совокупности, либо существует возможность их преобразования в такую совокупность (4.1). Другие случаи требуют иной обработки, которая выходит за сферу действия этого стандарта [10]. Несмотря на то, что приведенные технические приемы представлены в форме, приспособленной для расчета вручную, рекомендуется использовать электронный компьютер для хранения и анализа результатов межлабораторных испытаний. Измененная редакция. Изм. № 1. 4.1 Преобразование данных4.1.1 Для многих методов испытаний наблюдается зависимость показателей прецизионности от уровня результатов испытаний, поэтому изменчивость сообщенных результатов различается при переходе от пробы к пробе. Такое положение исправляют с помощью преобразования данных. Измененная редакция. Изм. № 1. 4.1.2 Рассчитывают лабораторные среднеквадратические отклонения Dj и среднеквадратические отклонения для дублей dj (приложение В) и строят графики зависимости их от средних значений по пробе mj. Если через точки, нанесенные на графике, можно провести две линии, параллельные оси значений m, тогда нет необходимости вводить преобразование. Если через точки, нанесенные на графике, можно построить прямые непараллельные оси значений m или кривые, построенные по этим точкам, могут быть описаны зависимостями D = f1(m) и d = f2(m), то необходимо вводить преобразование. 4.1.3 Зависимости D = f1(m) и d = f2(m) в общем случае не будут идентичны. Однако статистические процедуры этого стандарта требуют, чтобы и для повторяемости (сходимости) и для воспроизводимости было применено одно и то же преобразование. Обе зависимости комбинируют в единую зависимость в форме D = f(m), включающей фиктивную переменную Т, причем D теперь включает и d. Эта процедура учитывает различие между двумя зависимостями, если оно существует, и обеспечивает возможность выявления этого различия. В приложении Д приведены виды зависимостей и подходящие преобразования. Единую зависимость D = f(m) оценивают с помощью метода взвешенного линейного регрессионного анализа (приложение Е). Следует использовать взвешенную регрессию с итерациями, однако в большинстве случаев даже простая регрессия будет давать удовлетворительную аппроксимацию. Вывод весовых функций изложен в Е.2, а расчетная процедура для регрессионного анализа - в Е.3. Типичные формы зависимости D = f(m) даны в Д.1. Все они выражены в терминах параметра единого преобразования В. 4.1.4 Оценивание В и следующая за этим процедура преобразования суммированы в Д.1. Это включает статистические испытания значимости регрессии (т.е. является ли зависимость D =f(m) параллельной оси значений т) и значимости различия между зависимостями для повторяемости (сходимости) и воспроизводимости. Решения по испытаниям принимают на основе 5 %-ного уровня значимости. Если обнаружено, что различие между зависимостями существует или отсутствует подходящее преобразование, следует использовать альтернативные методы [1]. В этом случае невозможно проводить испытание с целью выявления систематического смещения лаборатории по всем пробам по 4.5 либо отдельно оценивать компоненту дисперсии по взаимодействию в соответствии с 5.1. 4.1.5 Если на 5 %-ном уровне значимости было показано, что значимая регрессия в форме D = f(m) существует, тогда соответствующее преобразование у = F(x), где х - сообщенный результат, выражают формулой
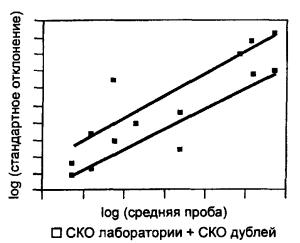
где К - постоянная величина. В этом случае все результаты следует соответствующим образом преобразовать и последующую часть анализа выполнять в терминах преобразованных результатов (Д.1). При выборе преобразования в конкретных случаях может потребоваться помощь квалифицированного статистика. На правильность решения о выборе типа преобразования по 4.6 могут влиять аномальные результаты. Пример - В таблице 1 представлены значения m, D и d с тремя значащими цифрами для восьми проб из приведенного в приложении Г примера. Соответствующие степени свободы приведены в скобках. D и d возрастают с ростом m, причем скорость возрастания падает по мере увеличения m. График зависимости этих величин в билогарифмических координатах (т.е. график зависимости log D и log d от log m) показывает, что вполне допустимо рассматривать эти точки как лежащие на двух прямых линиях (рисунок E.1). Расчеты, приведенные в Е.4, показывают, что градиенты этих линий одни и те же и оцениваются значением 0,638. Учитывая ошибки в оценке этого значения, для удобства можно принять градиент равным 2/3. Таблица 1
Одно и то же преобразование предназначено для повторяемости (сходимости) и воспроизводимости и выражено формулой
Так как постоянным множителем можно пренебречь, то преобразование сводят к извлечению кубического корня из сообщенных результатов (бромных чисел). Выполнение этой процедуры дает преобразованные данные, приведенные в таблице Г.2, в которой результаты после извлечения кубического корня приведены с тремя значащими цифрами. 4.2 Выявление аномальных результатов4.2.1 Сообщенные данные или, если принято решение о необходимости преобразования, преобразованные результаты изучают с целью выявления аномальных результатов. Они представляют собой значения, которые настолько отличаются от остальных, что единственное заключение, которое можно сделать, что они возникли вследствие ошибок в применении исследуемого метода или вследствие испытания по ошибке другой пробы. Можно использовать различные приемы, причем связанные с ними уровни значимости расходятся. Однако было найдено, что приемы, регламентированные в следующих разделах, являются подходящими для этого стандарта. Эти испытания основаны на предположении о нормальном распределении погрешностей [10]. 4.2.2 Однородность данных, используемых для определения повторяемости (сходимости) метода Первое испытание для выявления аномальных
результатов касается обнаружения противоречивых данных в парах результатов,
полученных при дублировании испытаний. Это испытание [3] включает расчет Пример - В случае, относящемся к приведенному в таблице Г.2 примеру, абсолютные разности между преобразованными результатами повторных испытаний, т.е. парами чисел, рассчитанными с точностью до третьего десятичного знака, приведены в таблице 2. Таблица 2
Самый большой размах составляет 0,078 для лаборатории G на пробе 3. Сумма квадратов всех размахов составляет 0,0422 + 0,0212 +,..., +0,0262 + 02 = 0,0439. В результате отношение, которое сравнивают с критическим значением в испытании по Кохрену, составляет
В примере используют 72 размаха, а в таблице Г.3 имеется критическое значение для 80 размахов, составляющее 0,1709. Следовательно, это отношение незначимо. 4.2.3 Однородность данных, используемых для определения воспроизводимости 4.2.3.1 Последующие испытания для выявления аномальных результатов относятся к установлению однородности данных, использованных при оценке воспроизводимости и предназначенных для обнаружения либо аномальной пары результатов от лаборатории на определенной пробе, либо аномальной серии результатов от какой-либо лаборатории на всех пробах. В обоих случаях подходящим оказывается испытание по Хокинсу [4]. Процедура включает образование среднего значения по каждой пробе или общего среднего по всем лабораториям по 4.5, образование отношения наибольшего абсолютного отклонения среднего значения пробы в лаборатории от среднего для пробы по всем лабораториям (или отклонение от среднего по всей таблице) к квадратному корню из соответствующих сумм квадратов по В.3. 4.2.3.2 Отношение, соответствующее наибольшему абсолютному отклонению, следует сравнивать с критическим значением на 1 %-ном уровне значимости, приведенным в таблице Г.4. В этом случае n представляет число ячеек-комбинаций «лаборатория ´ проба» для рассматриваемой пробы (или число средних по всем лабораториям), a v - число степеней свободы для суммы квадратов, которая является дополнением к квадрату, соответствующему рассматриваемой пробе. В испытании ячеек «лаборатория ´ проба» v относят к остальным пробам, однако в испытании средних значений по всем лабораториям v будет равно нулю. 4.2.3.3 Если значимый результат получают для отдельных проб, то соответствующие экстремальные значения следует отбросить, а процедуру испытания повторить. Если какие-либо экстремальные значения обнаружены среди итогов по лабораториям, то все результаты данной лаборатории следует отбросить. Если доля брака при испытании высока (более 10 %), то следует отказаться от такого испытания по выявлению аномальных результатов, вернуть все или некоторые аномальные результаты для дальнейшей обработки и принять произвольное решение, основанное на ситуации. Пример - Применение испытания по Хокинсу к средним значениям по ячейкам для пробы. Первый шаг состоит в том, чтобы рассчитать отклонения средних значений по ячейкам от соответствующих средних значений по пробам для всего массива данных. Результаты, рассчитанные с точностью до третьего десятичного разряда, представлены в таблице 3. Таблица 3
В ходе расчета для каждой пробы вычисляют сумму квадратов отклонений. Эти результаты, также рассчитанные с точностью до единиц в третьем десятичном разряде, представлены в таблице 3. В первую очередь испытывают ячейку с наибольшим экстремальным отклонением. Это отклонение получено лабораторией D на пробе 1. Экспериментальное значение отношения В* в испытании по критерию Хокинса равно
Критическое значение, соответствующее n = 9 ячейкам для пробы 1 и v = 56 степеням свободы для других проб, получают путем интерполяции значений из таблицы Г.4, равным 0,3729. Экспериментальное значение больше критического, поэтому результаты испытаний, полученные в лаборатории D на пробе 1, отбрасывают. Так как был отброшен аномальный результат, среднее значение, отклонения и сумму квадратов для пробы 1 пересчитывают, а процедуру выявления аномальных результатов повторяют. Следующей испытываемой ячейкой является ячейка с результатом, полученным лабораторией F на пробе 2. Экспериментальное значение отношения В* в испытании по Хокинсу для этой ячейки составляет
Критическое значение, соответствующее n = 9 ячейкам для пробы 1 и v = 55 степеням свободы, соответствующим алгебраическому дополнению, получают путем интерполяции значений из таблицы Г.4 равным 0,3756. Так как экспериментальное значение меньше критического, то продолжать процедуру браковки не нужно. 4.3 Браковка полного набора данных по пробе4.3.1 Межлабораторное среднеквадратическое отклонение и среднеквадратическое отклонение для повторных испытаний следует исследовать на предмет выявления «выпадающих» проб. Если исходные данные были подвергнуты преобразованию или какие-либо результаты были отброшены как аномальные, то следует вычислить новые значения среднеквадратических отклонений. Если среднеквадратическое отклонение для какой-либо пробы оказывается исключительно большим, его следует исследовать с целью выявления необходимости браковки всех результатов испытаний этой пробы. Для этого используют критерий Кохрена на 1 %-ном уровне значимости, если среднеквадратические отклонения основаны на одинаковом числе степеней свободы. Испытание включает вычисление отношения наибольшей из соответствующих сумм квадратов (межлабораторных или для повторных испытаний в зависимости от ситуации) к их общей сумме по В.2. Если экспериментальное значение отношения превосходит критическое, приведенное в таблице Г.3 с n в качестве числа проб и v в качестве степеней свободы для отдельного среднего квадратического отклонения, то все результаты для рассматриваемой пробы следует забраковать. В этом случае следует проверить, не обусловлено ли экстремальное среднеквадратическое отклонение применением неподходящего преобразования по 4.1 или необнаруженными аномальными результатами. 4.3.2 Не существует оптимального испытания для исследования однородности среднеквадратических отклонений, основанных на различных степенях свободы. Тем не менее распределение отношения максимальной дисперсии к дисперсии, средневзвешенной по всем остальным пробам, подчиняется F-распределению с v1 и v2 степенями свободы (В.4). В этом случае v1 - степени свободы для дисперсии, о которой идет речь, a v2 - степени свободы взвешенной дисперсии для остальных проб. Если экспериментальное значение отношения больше критического, приведенного в таблицах Г.6.1 - Г.6.5 и соответствующего уровню значимости 0,01/S, где S - число проб, то результаты для рассматриваемой пробы следует отвергнуть. Пример - Среднеквадратические отклонения преобразованных результатов испытаний после отбраковки пары результатов, полученных в лаборатории D на пробе 1, приведены в таблице 4 в возрастающем порядке средних значений по пробам, скорректированных с точностью до трех значащих цифр после запятой. Соответствующие степени свободы приведены в скобках. Таблица 4
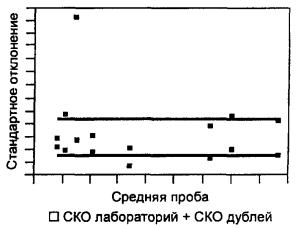
Исследования показывают, что выпадающие пробы среди них отсутствуют. Следует отметить, что среднеквадратические отклонения теперь не зависят от средних значений по пробам, что и было целью преобразования данных. Числовые значения в таблице 5, взятые из программы испытаний по определению бромных чисел, превышающих 100, иллюстрируют случай признания аномальными всех результатов по отдельной пробе. Таблица 5
4.3.3 При исследовании выявлено, что межлабораторное среднеквадратическое отклонение для пробы 93, равное 15,26, существенно больше, чем среднеквадратические отклонения для других проб. Необходимо отметить, что среднеквадратическое отклонение для повторных испытаний также велико. Так как степени свободы для межлабораторного среднеквадратического отклонения не одинаковы для различных проб, следует использовать испытание, основанное на отношении дисперсий (испытание по модифицированному критерию Фишера). Средневзвешенная дисперсия, не включающая пробу 93, представляет собой сумму сумм квадратов, деленную на общее число степеней свободы, т.е.
Затем рассчитывают дисперсионное отношение (15,26)2/19,96 = 11,66. Согласно таблицам Г.6.1 - Г.6.5 критическое значение, соответствующее уровню значимости 0,01/8 = 0,00125 для 8 и 63 степеней свободы, равно приблизительно 4. Это меньше экспериментального значения. Поэтому результаты для пробы 93 следует признать аномальными и отбросить. 4.3.4 Если степени свободы для отдельных проб одинаковы для всех проб, можно применять испытание по Кохрену. Критерий Кохрена будет представлять в этом случае отношение наибольшей суммы квадратов (проба 93) к сумме всех остальных сумм квадратов, т.е. 2,972/(1,132 + 0,992 +,...,+ 1,362) = 0,510. Этот результат больше критического значения 0,352, соответствующего n = 8 и v = 8 (таблица Г.3). Следовательно результаты, полученные на пробе 93, следует признать аномальными. Измененная редакция. Изм. № 1. 4.4 Оценивание результатов, заменяющих потерянные или забракованные данные4.4.1 Потерян или забракован один из двух результатов в серии повторных испытаний. Если один из пары результатов в серии повторных испытаний - дублей (уij1 или уij2) потерян или забракован, следует принять, что он имеет значение, равное значению другого результата в серии в соответствии с методом наименьших квадратов. 4.4.2 Потеряны или забракованы оба результата в серии повторных испытаний. Если оба результата в серии повторных испытаний - дублей потеряны, аij = (уij1 + уij2) следует оценивать суммой квадратов по взаимодействию «лаборатория ´ проба», включающей потерянные значения в значении суммы пар результатов всех комбинаций «лаборатория ´ проба» как неизвестные переменные. При этом следует игнорировать любую лабораторию или пробу, все результаты которой были забракованы, и использовать новые значения L и S. Оценки потерянных или отбракованных результатов находят по частным от производных этой суммы по каждой переменной, приравнивая их нулю, и последующим решением системы нормальных уравнений. Формулу (4) используют, когда следует оценить сумму одной пары. Если необходимо получить большее число оценок, можно использовать процедуру последовательного приближения. В этом случае сумму каждой пары оценивают по очереди, последовательно по формуле (4) с использованием новых значений L1, S1 и T1, которые содержат последние оценки других потерянных пар. Начальные значения для оценок могут быть основаны на подходящем среднем значении для пробы, и процесс обычно сходится к требуемому уровню точности после трех итераций. Более детальное изучение вопроса приведено в [7]. Если необходимо оценить значение суммы одной пары aij, оценку получают по формуле где S¢ = S минус число проб, признанных выпадающими согласно процедуре по 4.3; L1 - сумма оставшихся в i-й лаборатории пар результатов; S1 - сумма оставшихся для j-й пробы пар результатов; Т1 - общая сумма пар результатов, за исключением суммы потерянной пары аij. Пример - Два результата лаборатории D на пробе 1 были признаны аномальными и отброшены по 4.2.2. Поэтому а41 следует оценить. Сумма полных пар результатов, оставшихся в лаборатории D, равна 36,354. Сумма полных пар результатов, оставшихся для пробы 1, равна 19,845. Сумма всех полных пар результатов, за исключением а41, равна 348,358. Кроме того, S¢ = 8 и L = 9. Оценку а41 представляют выражением
Следовательно,
4.5 Выявление «выпадающих» лабораторийНа этой стадии остается выполнить еще одно испытание с целью выявления «выпадающих» лабораторий. В этом испытании определяют, является ли необходимой браковка всего набора результатов, полученных какой-либо отдельной лабораторией. Испытание невозможно было выполнить на более ранней стадии, за исключением того случая, когда отсутствуют потерянные или отброшенные отдельные результаты или пары результатов. Процедура и в этом случае включает испытание по критерию Хокинса (4.2.2). Испытание применяют к лабораторным средним значениям по всем пробам, включающим все оцененные результаты. Если результаты какой-либо лаборатории признают выпадающими по всем пробам и отбрасывают, то для других потерянных результатов, сохранившихся в массиве данных, следует рассчитать новые оценки по 4.4. Пример - Процедура в применении к лабораторным средним значениям, показанным ниже в таблице 6, соответствует приведенной в 4.2.3. Таблица 6
Отклонения лабораторных средних значений от общего среднего значения приведены в таблице 7 в единицах третьего десятичного знака вместе с суммой квадратов. Таблица 7
Экспериментальное значение отношения В*, полученное в испытании по критерию Хокинса, равно
Сравнение со значением, табулированным в таблице Г.4 для n = 9 и v = 0, показывает, что экспериментальное значение отношения незначимо и, следовательно, нет необходимости браковать всю серию результатов, полученных данной или какой-либо другой лабораторией. 4.6 Проверка правильности выбранного преобразованияНа этой стадии следует проверить, не являются ли выявленные аномальные результаты причиной, вызвавшей необходимость преобразования исходных данных. Для проверки, если необходимо, следует повторить процедуру, описанную в 4.1, после удаления аномальных результатов. Если выбрано новое преобразование, испытания по выявлению аномальных результатов следует повторить. Пример - В данном случае нет необходимости повторять расчеты согласно 4.1 с аномальной парой результатов, которая была удалена. 5 Дисперсионный анализ и вычисление оценок показателей прецизионностиАнализ проводят после проверки однородности опытных данных, преобразования исходных данных, если это оказалось необходимым, и отбраковки всех выпадающих результатов в соответствии с разделом 4. Начинают с конструирования таблицы дисперсионного анализа и заканчивают вычислением оценок показателей прецизионности. Измененная редакция. Изм. № 1. 5.1 Дисперсионный анализ5.1.1 Формирование сумм квадратов для нахождения суммы квадратов по взаимодействию «лаборатория ´ проба» 5.1.1.1 Все имеющиеся оцененные значения включают в массив исходных данных и выполняют приближенный дисперсионный анализ. Поправка на среднее значение
где L¢ = L минус число лабораторий, отброшенных по 4.5, минус число лабораторий, в которых после отбраковки по 4.2.2 отсутствуют результаты; S¢ = S минус число проб, отбракованных в соответствии с 4.3. Сумма квадратов по пробам равна
Сумма квадратов по лабораториям равна
Сумма квадратов по парам результатов равна
I (сумма квадратов по взаимодействию «лаборатория ´ проба» равна сумме квадратов по парам результатов минус сумму квадратов по лабораториям минус сумму квадратов по пробам. После исключения пар, содержащих оцененные значения, находим Е (сумму квадратов по повторным испытаниям)
Цель выполнения приближенного дисперсионного анализа состоит в том, чтобы получить минимальную оценку суммы квадратов по взаимодействию «лаборатория ´ проба» I. Затем, как показано в 5.1.2, оценку используют при получении суммы квадратов по лабораториям. При отсутствии в массиве исходных данных оцененных значений указанный выше дисперсионный анализ становится точным и процедуру по 5.1.2 следует пропустить. Пример - Поправка на среднее значение равна
Сумма квадратов по пробам равна
Сумма квадратов по лабораториям равна
Сумма квадратов по парам результатов равна
Сумма квадратов по повторным испытаниям равна
Это позволяет составить сводную таблицу 8. Таблица 8
5.1.2 Формирование сумм квадратов для прецизионного дисперсионного анализа В этом пункте оцененные значения пар в расчет не принимают и рассчитывают новые значения gj. Для прецизионного дисперсионного анализа составляют суммы квадратов [5]. Некорректированная сумма квадратов по пробам равна
где Sj = 2 (L¢ - число потерянных пар на j-й пробе). Некорректированная сумма квадратов по парам результатов равна
Сумма квадратов по лабораториям равна сумме квадратов по парам результатов минус сумму квадратов по пробам, минус минимальную оценку суммы квадратов по взаимодействию «лаборатория ´ проба»
Пример - Некорректированная сумма квадратов по пробам равна
Некорректированная сумма квадратов по парам результатов равна
Следовательно, сумма квадратов по лабораториям равна 1145,3329 - 1145,1834 - 0,1143 = 0,0352. Измененная редакция. Изм. № 1. 5.1.3 Степени свободы Число степеней свободы для лабораторий равно (L¢ - 1). Число степеней свободы для взаимодействия «лаборатория ´ проба» равно (L¢ - 1) (S¢ - 1) для полного массива исходных данных и уменьшается на единицу за счет каждой пары, которая была оценена. Число степеней свободы для повторных испытаний равно (L¢S¢) и уменьшается на единицу для каждой пары, которая содержит одно или два оцененных значения. Пример - В рассматриваемом примере имеется 8 проб и 9 лабораторий. Поскольку ни одна из лабораторий или проб не была исключена полностью из рассмотрения, то S¢ = 8 и L¢ = 9. Число степеней свободы по лабораториям равно L - 1 = 8. В случае отсутствия значений число степеней свободы для взаимодействия «лаборатория ´ проба» составляло бы (9 - 1) (8 - 1) = 56. Однако одна пара была оценена, следовательно, число степеней свободы для взаимодействия «лаборатория ´ проба» равно 55. Число степеней свободы для повторных испытаний при отсутствии оцененных значений было бы равно 72. Однако в рассматриваемом случае одна пара была оценена и поэтому число степеней свободы для повторных испытаний равно 71. 5.1.4 Средние квадраты и дисперсионный анализ Средний квадрат в каждом случае равен сумме квадратов, деленной на число степеней свободы. Это позволяет составить следующую таблицу дисперсионного анализа (таблица 9). Таблица 9
Отношение МL/МLS имеет F-распределение с соответствующими степенями свободы для лабораторий и взаимодействия по В.4. Если это отношение превосходит 5 %-ный критический уровень, приведенный в таблицах Г.6.1 - Г.6.5, то предполагают наличие смещения между лабораториями, и руководитель программы должен быть проинформирован в соответствии с п. 3.4. В этом случае могут оказаться необходимыми дальнейшие работы по стандартизации метода испытаний. Пример - Результаты дисперсионного анализа представлены в таблице 10. Таблица 10
Значение отношения МL/МLS = 0,0044 / 0,002078 равно 2,117, и оно превосходит 5 %-ный критический уровень, полученный из таблицы Г.6.1, что указывает на наличие смещения между лабораториями. 5.2 Математические ожидания средних квадратов и вычисление оценок показателей прецизионностиИзмененная редакция. Изм. № 1. 5.2.1 Математические ожидания средних квадратов, рассчитанные по данным, в которых отсутствуют оцененные значения Для полного массива данных, не содержащих оцененных значений, математические ожидания равны: лаборатории: «лаборатория ´ проба»: повторные испытания: где
При расчете математических ожиданий средних
квадратов по данным, содержащим оценочные значения, перед лаборатории: «лаборатория ´ проба»: повторные испытания: где
где n - число результатов, фактически полученных в i-й лаборатории на j-й пробе; Ni - число результатов, полученных в i-й лаборатории; N¢ - общее число фактически полученных результатов минус число отбракованных результатов; К - число L´S ячеек (таблица B.1), которые содержат не менее одного незабракованного результата. Если ячейки, содержащие только один результат, отсутствуют, то a = g = 2. Примечание - Выводы основаны на допущении, что эффекты обеих независимых переменных, лаборатории и пробы, являются «случайными эффектами». Пример - Для рассматриваемого примера с 8 пробами и 9 лабораториями
5.2.3 Вычисление оценок показателей прецизионности Измененная редакция. Изм. № 1. 5.2.3.1 Повторяемость (сходимость) метода Дисперсия, характеризующая повторяемость (сходимость) метода, равна удвоенному среднему квадрату по повторным испытаниям. Оценка повторяемости (сходимости) метода равна произведению среднеквадратического отклонения, характеризующего повторяемость (сходимость) метода, на коэффициент t для соответствующего числа степеней свободы (таблица Г.5) и доверительной вероятности 95 % при двусторонней постановке задачи. Вычисленную таким образом оценку следует округлить до последнего разряда, использованного в отчете о результатах испытаний, что является следствием определения понятия повторяемость (сходимость) метода. Примечание - Если было применено преобразование у = f(x), то следует учитывать, что
где r(х), r(у) являются соответствующими функциями повторяемости (сходимости) (таблица Д.1). Аналогичная зависимость связывает функции воспроизводимости R(х), R(у). Пример Дисперсия, характеризующая условия повторяемости
(сходимости), равна Повторяемость (сходимость) величин Повторяемость (сходимость) величин 5.2.3.2 Воспроизводимость метода Дисперсия, характеризующая воспроизводимость метода, равна
Она может быть вычислена с помощью формулы (14). Дисперсия, характеризующая условия воспроизводимости, равна где обозначения имеют то же значение, что и в 5.1.4 и 5.2.2. Оценка воспроизводимости метода равна произведению среднего квадратического отклонения, характеризующего воспроизводимость метода, на коэффициент t для соответствующего числа степеней свободы (таблица Г.5), и доверительной вероятности 95 % при двусторонней постановке задачи. Формула (15) дает приблизительную оценку числа степеней свободы для дисперсии, характеризующей условия воспроизводимости, где r1, r2 и r3 - три члена формулы (14), представленные в той же последовательности; vLS - число степеней свободы дисперсии для взаимодействия «лаборатория ´ проба»; v - число степеней свободы дисперсии для повторных испытаний (дублей). Оценку воспроизводимости метода следует округлить до последнего разряда, использованного в отчете о результатах испытаний, что является следствием определения понятия «воспроизводимость метода». Значительное смещение между лабораториями приводит к потере общего числа степеней свободы, оцененного с помощью формулы (15). Если дисперсия, характеризующая условия воспроизводимости, основана менее чем на 30 степенях свободы, руководитель программы исследования должен быть проинформирован (возможно, будут необходимы работы по дальнейшей стандартизации метода). Пример - Дисперсия, характеризующая воспроизводимость метода, равна
v = 7188 / (39 + 60 + 1) = 72 (результат округлен до ближайшей значащей цифры в целой части числа). Воспроизводимость величины у равна Воспроизводимость величины х равна 5.3 Раздел метода испытаний «Показатели прецизионности»После того, как показатели прецизионности метода испытаний были установлены в соответствии с настоящим стандартом, их включают в документ, регламентирующий метод испытаний, в следующей форме:
Эти значения показателей прецизионности получены путем последовательного использования определений и процедур ИСО 4259. Измененная редакция. Изм. № 1. 6 Повторяемость (сходимость) метода r и воспроизводимость метода RЗначения этих показателей оценивают с помощью дисперсионного анализа (двухфакторная схема с повторными испытаниями), примененного к результатам, полученным в ходе выполнения статистически обоснованной программы межлабораторных исследований. В соответствии с этой программой каждая из ряда лабораторий испытывает набор проб. Значения показателей повторяемости (сходимости) и воспроизводимости метода включают в каждый документ, регламентирующий метод испытаний. Следует отметить, что последний показатель всегда превосходит первый при условии, что показатели выведены в соответствии с рекомендациями [1]. Статистическое обоснование формул, примененных в этом разделе, приведено в приложении И. 6.1 Повторяемость (сходимость) метода rБольшинство лабораторий не проводят на каждой пробе более одного испытания для целей рутинного контроля качества, за исключением необычных обстоятельств (например, в случае спора или если оператор желает убедиться, что применяемые им технические приемы удовлетворительны). В этих обстоятельствах, когда получено несколько результатов, желательно проверить совместимость результатов повторных испытаний с требованиями повторяемости (сходимости) метода. Соответствующая процедура приведена в 6.1.1. Кроме того, полезно знать, какую степень доверия можно приписать среднему значению полученных результатов. Метод ее определения приведен в 6.1.2. 6.1.1 Приемлемость результатов Если в условиях повторяемости (сходимости) метода получены только два результата и расхождение между ними равно или меньше r, оператор может считать, что его работа находится под контролем. Он может принять среднее значение двух результатов в качестве оцененного значения определяемого свойства. Если расхождение двух результатов превышает r, оба результата считают подозрительными и получают дополнительно не менее трех результатов. После этого рассчитывают разность наиболее удаленного результата и среднего значения остальных результатов с учетом первых двух. Эту разность сравнивают с новым значением r1 которое следует рассчитать вместо r. Значение r1, рассчитывают по формуле
где k - общее число полученных результатов. Если разность меньше или равна r1, то все полученные результаты следует считать приемлемыми. Если разность более r1 отбрасывают наиболее удаленный результат и повторяют изложенную в этом пункте процедуру браковки до получения приемлемой группы результатов. Среднее значение приемлемых результатов следует принять в качестве оцененного значения определяемого свойства. Однако если из общего числа не более 20 было отбраковано два или более результатов, то процедуру выполнения испытаний и аппаратуру следует проверить и, если возможно, выполнить новую серию испытаний. Если один оператор, результаты работы которого удовлетворяют требованиям прецизионности метода испытаний, получает серию из k результатов в условиях повторяемости (сходимости) метода и среднее значение этой серии равно X, то с 95 %-ной доверительной вероятностью можно допустить, что истинное значение определяемой характеристики свойства m находится внутри границ
где Подобным образом при односторонней постановке задачи, когда фиксируют только одну границу (верхнюю или нижнюю), с 95 %-ной доверительной вероятностью можно принять, что истинное значение определяемой характеристики свойства m ограничено областью значений
или
Коэффициент 0,59 - это отношение Если обнаружено, что воспроизводимость метода R значительно превосходит повторяемость (сходимость) метода r, то следует подвергнуть анализу причины столь большого значения отношения R/r и, насколько возможно, улучшить метод. Измененная редакция. Изм. № 1. 6.2 Воспроизводимость метода R6.2.1 Приемлемость результатов Приведенная процедура предназначена для определения приемлемости результатов, полученных различными лабораториями в процессе обычной повседневной деятельности, по степени их согласованности с воспроизводимостью метода испытаний. При возникновении спора между поставщиком и получателем следует действовать в соответствии с процедурой, изложенной в разделах 7 - 9. Если в двух лабораториях получены единичные результаты и их разность меньше или равна R, оба результата следует считать приемлемыми. Среднее значение этих результатов вернее, чем каждый из результатов в отдельности, и его следует рассматривать как оцененное значение определяемого свойства. Если разность указанных результатов превышает R, оба результата считают подозрительными. В этом случае каждой лаборатории следует получить дополнительно не менее трех приемлемых результатов по 6.1.1. Разность средних значений всех приемлемых результатов от каждой лаборатории следует оценить на соответствие, используя новое значение R2 вместо R. R2 выражают формулой где R - воспроизводимость метода; r - повторяемость (сходимость) метода; k1 - число результатов, полученных в первой лаборатории; k2 - число результатов, полученных во второй лаборатории. Если разность этих средних значений меньше или равна R2, эти средние значения считают приемлемыми, и их общее среднее значение следует рассматривать как оцененное значение определяемого свойства. Если разность между средними значениями превосходит R2, следует действовать в соответствии с процедурой, изложенной в разделах 7 - 9. Если более двух лабораторий, т.е. (N + 1) > 2, представили по одному или более приемлемых результатов, находят разность наиболее удаленного лабораторного среднего значения и среднего значения остальных N лабораторных средних значений. Полученную разность следует сравнивать с R3, значение которой рассчитывают по формулам: Значение R1 определяют согласно формуле (18). Она соответствует наиболее удаленному лабораторному среднему значению. Если разность меньше или равна R3 по абсолютному значению, то все результаты следует рассматривать как приемлемые, и их среднее значение принимают как оцененное значение определяемого свойства. Если разность превосходит R3, наиболее удаленное лабораторное среднее значение отбрасывают. Используя формулы (22) и (23), сравнение повторяют до получения приемлемой группы средних значений по лабораториям. Среднее значение этих лабораторных средних значений принимают в качестве оцененного значения определяемого свойства. Однако если из общего числа не более 20 было отбраковано два или более лабораторных средних значений, то процедуру выполнения испытаний и аппаратуру следует проверить и, если возможно, выполнить новую серию испытаний. 6.2.2 Доверительные границы Если в N лабораториях получены один
или более результатов в условиях повторяемости (сходимости) и воспроизводимости
метода, из которых образуют общее среднее для лабораторных средних значений
Подобным образом при односторонней постановке задачи, когда фиксируют только одну границу (верхнюю или нижнюю), с 95 %-ной доверительной вероятностью можно принять, что истинное значение определяемой характеристики свойства m ограничено областью значений
или
Кроме того, эти формулы позволяют данной лаборатории (N = 1) определить доверительную границу, которую можно приписать среднему значению полученных результатов при сравнении с истинным значением. 7 Спецификации (технические условия на продукцию)7.1 Назначение спецификацийНазначением спецификаций (технических условий) является установление фиксированной границы или границ для истинного значения рассматриваемого свойства (показателя качества). Однако на практике это истинное значение невозможно установить точно. Заданное свойство определяют в лаборатории с помощью стандартного метода испытаний. Результаты, полученные с использованием стандартного метода, как правило, демонстрируют некоторое рассеяние, что и определяют с помощью повторяемости (сходимости) и воспроизводимости метода. Поэтому в отношении истинного значения определяемого свойства всегда существует некоторая неопределенность. Соответствие требованиям спецификаций проверяют в соответствии с разделами 8 и 9. При предварительном соглашении между поставщиком и потребителем можно использовать альтернативные процедуры, изложенные в приложении К. 7.2 Составление спецификаций7.2.1 Границы допускаемых значений определяемого свойства продукции обычно устанавливают с помощью спецификаций. Чтобы исключить неопределенность, такие границы, как правило, должны быть выражены в соответствующей форме, а именно, «не менее...» или «не более...». Границы бывают двух типов. - двусторонние границы, верхняя и нижняя, например, «вязкость не менее 5 мм2/с и не более 10 мм2/с»; «точка кипения (100±0,5) °С». - односторонняя граница, верхняя или нижняя, например, «массовая доля серы не более 2 %»; «концентрация свинца не более 3,0 г/л»; «растворимость битума не менее 99 %». Одностороннюю границу назначают, если существует другая предполагаемая граница, которая практически приводит к ситуации с двусторонней границей, что и имеет место в большинстве случаев. Это демонстрируют приведенные выше примеры, в которых другой предполагаемой границей являются 0 %, 0 г/л и 100 % соответственно. В случае истинной односторонней границы, например, для «температуры вспышки не менее 60 °С», приведенные ниже соображения не применимы. В этом и последующих разделах, обозначает верхнюю границу, а А2 обозначает нижнюю. При назначении граничных значений в спецификации следует принимать в расчет воспроизводимость того метода испытаний, который допущен для проверки соответствия требованиям данной спецификации, по следующим правилам: - в случае двусторонних границ (А1 и А2) специально обозначенное поле допуска (установленное или предполагаемое) не должно быть меньше четырехкратного значения воспроизводимости допущенного к испытаниям метода R, т.е.
- в случае односторонних границ (А1 или А2) специально обозначенное поле допуска не должно быть меньше удвоенного значения воспроизводимости допущенного к испытаниям метода R, т.е.
Требования настоящего стандарта распространяются на спецификации, составленные в соответствии с указанными правилами. Если по практическим причинам ширина поля допуска (А1 - А2) оказывается меньше 4R, результаты испытаний будут иметь сомнительную ценность при решении вопроса, удовлетворяет ли требованиям спецификации испытанная проба или нет. Из соображений статистики желательно, чтобы (А1 - А2) было существенно больше 4R. Если это условие не выполняется, то следует принять один или оба способа действия: а) граничные значения, установленные в спецификации, следует изучить с целью определения возможности расширить границы поля допуска и за счет этого привести их в соответствие с требованиями к прецизионности метода испытаний; б) провести исследование метода испытаний с целью определения возможности улучшить показатели прецизионности метода. Цель исследования состоит в том, чтобы привести в соответствие прецизионность метода испытаний и протяженность поля допуска, установленную в спецификации. Измененная редакция. Изм. № 1. 8 Контроль качества продукции на соответствие требованиям спецификацийКонтроль качества продукции на соответствие требованиям спецификаций позволяет поставщику и получателю принять решение о соответствии качества продукта требованиям спецификации при наличии одного результата испытаний. Если после изучения этого результата у получателя возникнет необходимость принимать какие-либо действия, то рекомендуется процедура, изложенная в разделе 9. 8.1 Граничные значения результатов испытаний у поставщикаПоставщик, не имеющий другой информации об истинном значении определяемой характеристики, кроме отдельного результата испытаний, с 95 %-ной доверительной вероятностью может быть уверен, что продукт соответствует требованиям спецификации, если результат испытаний Х такой, что: в случае односторонней верхней границы А1 в случае односторонней нижней границы А2 в случае двусторонней границы (А1 и А2) требуется соблюдение обоих условий (6.1.2). Применение формул (27) и (28) следует интерпретировать как руководство для поставщика, а не как его обязательство. Факт нахождения сообщенного значения в области между установленным в спецификации значением и граничным значением, установленным в соответствии с формулами (27) и/или (28), не является доказательством отсутствия соответствия требованиям спецификации. 8.2 Граничные значения результатов испытаний у получателяПолучатель, не имеющий другой информации об истинном значении определяемой характеристики, кроме отдельного результата испытаний, с 95 %-ной доверительной вероятностью может быть уверен, что продукт не соответствует требованиям спецификации при условии, что результат испытаний Х такой, что: в случае односторонней верхней границы A1
в случае односторонней нижней границы А2
В случае двусторонней границы (А1 и А2) требуется выполнение любого из указанных условий. 9 Правила принятия или отклонения результатов испытаний в случае возникновения спораЕсли поставщик и получатель не могут прийти к соглашению о качестве продукта на основе полученных ими результатов испытаний, следует выполнить следующую процедуру. 9.1 Каждая лаборатория должна отвергнуть свои первоначальные результаты, и им следует получить не менее трех других приемлемых результатов на своей собственной контрольной пробе таким образом, чтобы обеспечить выполнение данной работы в условиях повторяемости (сходимости). Затем следует вычислить среднее значение полноценных, приемлемых результатов в каждой лаборатории, отбрасывая при этом выпадающие результаты так, как указано в 6.1.1. Если новые испытания не позволяют разрешить спор, продолжают выполнять процедуру разрешения спора. Пусть
А1 - верхняя граница по спецификации; А2 - нижняя граница по спецификации; где
Это означает, что средние значения
9.1.1 Если продукт принимают при условии, что В последнем случае невозможно с уверенностью установить, соответствует ли продукт требованиям спецификации или нет. Поэтому разрешение спора возможно только путем переговоров. Поправка. ИУС № 6 2002 г. 9.1.2 Если спор продолжают вне зависимости от величины разности
9.2 В случае продолжения спора двум лабораториям необходимо вступить в контакт друг с другом и сравнить процедуры выполнения испытаний и аппаратуру. Вслед за этими исследованиями обе лаборатории должны провести испытания каждая на своей контрольной пробе с целью установления взаимного соответствия. В каждой лаборатории вычисляют среднее значение, по крайней мере, из трех приемлемых результатов. Эти средние значения сравнивают так, как указано в 9.1. 9.3 Если разногласия остаются, следует пригласить
третью лабораторию (нейтральную, экспертную или по соглашению сторон) для
проведения испытаний, используя третью контрольную пробу. Допустим, что если если Измененная редакция. Изм. № 1. 9.4 Если разность наиболее удаленного среднего, принадлежащего одной из лабораторий, и среднего, образованного из средних значений, принадлежащих двум другим лабораториям, больше R3, то следует выполнить следующую процедуру: если если ПРИЛОЖЕНИЕ А
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L = 5 |
L = 6 |
L = 7 |
|||||||||||||||||||||||||||||||||
|
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Р: |
0 |
4 |
|
|
|
|
|
|
|
|
|
Р: |
0 |
3 |
|
|
|
|
|
|
|
|
|
P: |
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
1 |
5 |
|
|
|
|
|
|
|
|
|
|
1 |
4 |
11 |
|
|
|
|
|
|
|
|
|
1 |
4 |
7 |
|
|
|
|
|
|
|
|
|
|
2 |
6 |
11 |
|
|
|
|
|
|
|
|
|
2 |
5 |
7 |
|
|
|
|
|
|
|
|
|
2 |
4 |
6 |
17 |
|
|
|
|
|
|
|
|
|
3 |
6 |
9 |
|
|
|
|
|
|
|
|
|
3 |
5 |
7 |
14 |
|
|
|
|
|
|
|
|
3 |
4 |
5 |
9 |
|
|
|
|
|
|
|
|
|
4 |
7 |
8 |
16 |
|
|
|
|
|
|
|
|
4 |
5 |
6 |
10 |
|
|
|
|
|
|
|
|
4 |
5 |
5 |
7 |
13 |
|
|
|
|
|
|
|
|
5 |
7 |
8 |
12 |
|
|
|
|
|
|
|
|
5 |
6 |
6 |
8 |
15 |
|
|
|
|
|
|
|
5 |
5 |
5 |
6 |
9 |
19 |
|
|
|
|
|
|
|
6 |
7 |
8 |
11 |
19 |
|
|
|
|
|
|
|
6 |
6 |
6 |
8 |
11 |
|
|
|
|
|
|
|
6 |
5 |
5 |
6 |
8 |
12 |
|
|
|
|
|
|
|
7 |
7 |
8 |
10 |
15 |
|
|
|
|
|
|
|
7 |
6 |
6 |
7 |
10 |
15 |
|
|
|
|
|
|
7 |
5 |
5 |
6 |
7 |
10 |
15 |
|
|
|
|
|
|
8 |
7 |
8 |
9 |
13 |
|
|
|
|
|
|
|
8 |
6 |
6 |
7 |
9 |
12 |
|
|
|
|
|
|
8 |
5 |
5 |
6 |
7 |
8 |
12 |
20 |
|
|
|
|
|
9 |
7 |
8 |
9 |
11 |
17 |
|
|
|
|
|
|
9 |
6 |
6 |
7 |
8 |
10 |
15 |
|
|
|
|
|
9 |
5 |
5 |
6 |
6 |
8 |
10 |
14 |
|
|
|
|
L = 8 |
L = 9 |
L = 10 |
|||||||||||||||||||||||||||||||||
|
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Р: |
0 |
3 |
|
|
|
|
|
|
|
|
|
Р: |
0 |
2 |
|
|
|
|
|
|
|
|
|
Р: |
0 |
2 |
8 |
|
|
|
|
|
|
|
|
|
|
1 |
3 |
5 |
|
|
|
|
|
|
|
|
|
1 |
3 |
4 |
|
|
|
|
|
|
|
|
|
1 |
3 |
4 |
11 |
|
|
|
|
|
|
|
|
|
2 |
4 |
5 |
9 |
|
|
|
|
|
|
|
|
2 |
3 |
4 |
7 |
|
|
|
|
|
|
|
|
2 |
3 |
4 |
5 |
12 |
|
|
|
|
|
|
|
|
3 |
4 |
5 |
7 |
14 |
|
|
|
|
|
|
|
3 |
3 |
4 |
5 |
9 |
|
|
|
|
|
|
|
3 |
3 |
3 |
4 |
6 |
13 |
|
|
|
|
|
|
|
4 |
4 |
4 |
6 |
9 |
20 |
|
|
|
|
|
|
4 |
4 |
4 |
5 |
6 |
11 |
|
|
|
|
|
|
4 |
3 |
4 |
4 |
5 |
7 |
14 |
|
|
|
|
|
|
5 |
4 |
4 |
5 |
7 |
11 |
|
|
|
|
|
|
5 |
4 |
4 |
5 |
6 |
7 |
12 |
|
|
|
|
|
5 |
3 |
4 |
4 |
5 |
6 |
8 |
14 |
|
|
|
|
|
6 |
4 |
4 |
5 |
6 |
8 |
13 |
|
|
|
|
|
6 |
4 |
4 |
4 |
5 |
6 |
9 |
14 |
|
|
|
|
6 |
3 |
4 |
4 |
4 |
5 |
6 |
9 |
14 |
|
|
|
|
7 |
4 |
4 |
5 |
6 |
7 |
10 |
16 |
|
|
|
|
7 |
4 |
4 |
4 |
5 |
6 |
7 |
10 |
15 |
|
|
|
7 |
3 |
4 |
4 |
4 |
5 |
6 |
7 |
9 |
14 |
|
|
|
8 |
4 |
5 |
5 |
6 |
6 |
8 |
11 |
18 |
|
|
|
8 |
4 |
4 |
4 |
5 |
5 |
6 |
8 |
10 |
16 |
|
|
8 |
3 |
4 |
4 |
4 |
5 |
5 |
6 |
7 |
10 |
14 |
|
|
9 |
4 |
5 |
5 |
5 |
6 |
7 |
9 |
13 |
|
|
|
9 |
4 |
4 |
4 |
5 |
5 |
6 |
7 |
8 |
11 |
18 |
|
9 |
4 |
4 |
4 |
4 |
4 |
5 |
6 |
6 |
8 |
10 |
|
L = 11 |
L = 12 |
L = 13 |
|||||||||||||||||||||||||||||||||
|
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Р: |
0 |
2 |
4 |
|
|
|
|
|
|
|
|
Р: |
0 |
2 |
4 |
|
|
|
|
|
|
|
|
Р: |
0 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
5 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
5 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
12 |
|
|
|
|
|
|
|
|
2 |
3 |
3 |
3 |
7 |
|
|
|
|
|
|
|
2 |
2 |
3 |
4 |
6 |
14 |
|
|
|
|
|
|
2 |
2 |
3 |
3 |
4 |
8 |
|
|
|
|
|
|
|
3 |
3 |
3 |
4 |
5 |
8 |
|
|
|
|
|
|
3 |
3 |
3 |
3 |
4 |
6 |
11 |
|
|
|
|
|
3 |
2 |
3 |
3 |
4 |
5 |
7 |
14 |
|
|
|
|
|
4 |
3 |
3 |
4 |
4 |
6 |
8 |
18 |
|
|
|
|
4 |
3 |
3 |
3 |
4 |
5 |
6 |
9 |
|
|
|
|
4 |
3 |
3 |
3 |
3 |
4 |
5 |
7 |
10 |
|
|
|
|
5 |
3 |
3 |
4 |
4 |
5 |
6 |
9 |
15 |
|
|
|
5 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
9 |
16 |
|
|
5 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
9 |
15 |
|
|
6 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
9 |
14 |
|
|
6 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
9 |
13 |
|
6 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
8 |
|
|
7 |
3 |
3 |
3 |
4 |
4 |
5 |
5 |
7 |
9 |
13 |
|
7 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
5 |
6 |
8 |
|
7 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
5 |
6 |
|
|
8 |
3 |
3 |
3 |
4 |
4 |
4 |
5 |
6 |
7 |
9 |
|
8 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
5 |
5 |
6 |
|
8 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
5 |
|
|
9 |
3 |
3 |
3 |
4 |
4 |
4 |
5 |
5 |
6 |
7 |
|
9 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
5 |
6 |
|
9 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
5 |
|
L = 14 |
L = 15 |
L = 16 |
|||||||||||||||||||||||||||||||||
|
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Р: |
0 |
2 |
3 |
|
|
|
|
|
|
|
|
Р: |
0 |
2 |
2 |
13 |
|
|
|
|
|
|
|
Р: |
0 |
1 |
2 |
5 |
|
|
|
|
|
|
|
|
|
1 |
2 |
2 |
3 |
7 |
|
|
|
|
|
|
|
1 |
2 |
2 |
3 |
5 |
19 |
|
|
|
|
|
|
1 |
2 |
2 |
3 |
4 |
8 |
|
|
|
|
|
|
|
2 |
2 |
2 |
3 |
4 |
6 |
12 |
|
|
|
|
|
2 |
2 |
2 |
3 |
3 |
4 |
7 |
|
|
|
|
|
2 |
2 |
2 |
2 |
3 |
4 |
5 |
9 |
|
|
|
|
|
3 |
2 |
2 |
3 |
3 |
4 |
5 |
8 |
18 |
|
|
|
3 |
2 |
2 |
3 |
3 |
3 |
4 |
6 |
9 |
|
|
|
3 |
2 |
2 |
2 |
3 |
3 |
4 |
4 |
6 |
9 |
|
|
|
4 |
2 |
3 |
3 |
3 |
3 |
4 |
5 |
7 |
11 |
|
|
4 |
2 |
2 |
3 |
3 |
3 |
4 |
4 |
5 |
7 |
10 |
|
4 |
2 |
2 |
2 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
|
|
5 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
8 |
|
5 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
|
5 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
|
|
6 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
|
6 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
|
6 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
4 |
4 |
|
|
7 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
5 |
|
7 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
|
7 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
4 |
|
|
8 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
4 |
|
8 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
|
8 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
9 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
4 |
4 |
|
9 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
9 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
ПРИЛОЖЕНИЕ Б
(справочное)
Формулы для расчета необходимого числа проб (см. 3.1.4)
Результаты испытаний, полученные при выполнении пилотной программы, подвергают дисперсионному анализу. В итоге получают грубые оценки трех компонент дисперсии, а именно:
![]() - для повторных испытаний;
- для повторных испытаний;
![]() - для взаимодействия
«лаборатория ´ проба»;
- для взаимодействия
«лаборатория ´ проба»;
![]() - для лабораторий.
- для лабораторий.
После подстановки L, Р и Q в формулу (15) (см. 5.2.3.2) для расчета степеней свободы для условий воспроизводимости формула принимает вид
где Р - отношение ![]() /
/![]() ;
;
Q - отношение ![]() /
/![]() ;
;
v - степени свободы для воспроизводимости метода;
L - число лабораторий;
S - число проб.
Формулу (Б.1) приводят к виду
aS + b = 0,
где ![]()
![]() .
.
Следовательно,
![]() (Б.2)
(Б.2)
дает значения S для данных значений L, Р, Q и v.
В таблице A.1 значения S основаны на v = 30. Для дробных значений Р и Q значения S могут быть оценены с помощью квадратичной интерполяции (второго порядка) табличных значений.
ПРИЛОЖЕНИЕ В
(обязательное)
Виды испытаний и обозначения
Испытания подразделяют на три вида:
по критерию Кохрена,
по критерию Хокинса;
F - испытание (испытание отношения дисперсий).
В настоящем стандарте используют следующие обозначения:
S - число проб;
L - число лабораторий;
i - индекс, обозначающий порядковый номер лаборатории;
j - индекс, обозначающий порядковый номер пробы;
х - результат отдельного испытания;
а - сумма результатов, полученных при дублировании испытаний, т.е. при повторных испытаниях, выполняемых практически без перерыва;
е - разность результатов, полученных при дублировании испытаний, т.е. при повторных испытаниях, выполняемых практически без перерыва;
v - число степеней свободы.
Форма записи результатов испытаний приведена в таблицах B.1 и В.2.
Таблица B.1 - Результаты, полученные при дублировании испытаний в каждой из L лабораторий на S пробах, и средние значения, соответствующие этим пробам, mj
|
Значение для пробы |
||||
|
1 |
2 |
j |
S |
|
|
1 |
x111 |
x121 |
x1j1 |
x1S1 |
|
x112 |
x122 |
x1j2 |
x1S2 |
|
|
2 |
x211 |
x221 |
x2j1 |
x2S1 |
|
x212 |
x222 |
x2j2 |
x2S2 |
|
|
i |
xi11 |
xi21 |
xij1 |
xiS1 |
|
xi12 |
xi22 |
xij2 |
xiS2 |
|
|
L |
xL11 |
xL21 |
xLj1 |
xLS1 |
|
xL12 |
xL22 |
xLj2 |
xLS2 |
|
|
Сумма |
g1 |
g2 |
gj |
gS |
|
Среднее значение |
m1 |
m2 |
mj |
mS |
|
Примечание - Если необходимо преобразование исходных данных типа у = F(х) по 4.1, то используют символы yjj1и yij2 вместо xjj1и xij2. |
||||
Форма заполнения приведена в таблице В.2.
Таблица В.2 - Суммы результатов, полученные при дублировании испытаний, итоги по лабораториям hi и итоги по пробам gj
|
Значение для пробы |
|||||
|
1 |
2 |
j |
S |
Сумма |
|
|
1 |
a11 |
a12 |
a1j |
a1S |
h1 |
|
2 |
a21 |
a22 |
a2j |
a2S |
h2 |
|
i |
аi1 |
аi2 |
аij |
аiS |
hi |
|
L |
аL1 |
аL2 |
аLj |
аLS |
hL |
|
Сумма |
g1 |
g2 |
gj |
gS |
Т |
аij = xij1 + xij2 (или аij = yij1 + yij2, если используют преобразование).
eij = xij1 - xij2 (или eij = yij1 - yij2, если используют преобразование).
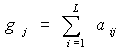 ,
, ![]() ,
,
![]() ,
, ![]() .
.
Если в заполненной таблице отсутствуют какие-либо результаты, то делитель в выражении для mj уменьшают соответствующим образом.
B.1 Суммы квадратов и дисперсии (4.1)
Дисперсия дублей (повторных испытаний) ![]() для j-й пробы
для j-й пробы
где L - число степеней свободы для (повторных испытаний) дублей на j-й пробе. Если любой или оба результата в паре «лаборатория ´ проба» в ij-й ячейке потеряны, то соответствующий член в числителе пропускают, а коэффициент L уменьшают на единицу.
Дисперсия значений, средних по ячейкам ![]() , для j-й пробы равна
, для j-й пробы равна
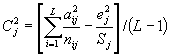 . (В.2)
. (В.2)
Лабораторная дисперсия ![]() для j-й
пробы, т.е. дисперсия результатов, которые приписывают отдельной лаборатории,
для j-й пробы равна
для j-й
пробы, т.е. дисперсия результатов, которые приписывают отдельной лаборатории,
для j-й пробы равна
![]() , (В.3)
, (В.3)
где ![]() , (В.4)
, (В.4)
nij - число результатов, полученных i-й лабораторией на j-й пробе;
Sj - общее число результатов, полученных на j-й пробе;
L - число ячеек для j-й пробы, содержащих, по крайней мере, один результат.
Число степеней свободы лабораторной дисперсии для j-й пробы приближенно определяют с помощью выражения [6]
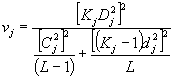 . (В.5)
. (В.5)
vj округляют до ближайшего целого числа.
Если любой или оба результата в паре для ij-й ячейки потеряны, то коэффициент L уменьшают на единицу.
Если оба результата в паре для ij-й ячейки потеряны, то коэффициент (L - 1) уменьшают на единицу.
В.2 Испытание по критерию Кохрена
Наибольшая сумма квадратов SSk, плохо согласующаяся с серией из n взаимно независимых сумм квадратов, каждая из которых основана на v степенях свободы, может быть испытана на однородность согласно выражению
Критерий
Кохрена = ![]() . (В.6)
. (В.6)
Экспериментальное значение полученного отношения не
изменится, если суммы квадратов заменяют средними квадратами (оценками
дисперсии). Если вычисленное значение отношения превосходит критическое
значение, приведенное в таблице Г.3, то сумма квадратов SSk значимо превосходит другие суммы с доверительной вероятностью 99 %.
Примеры использования SSi относятся к значениям ![]() и
и ![]() по формуле (B.1).
по формуле (B.1).
В.3 Испытание по критерию Хокинса
В.3.1 Экстремальное значение в серии данных может быть испытано как аномальное (выпадающее) сравнением его отклонения от среднего значения серии данных, деленного на квадратный корень из суммы квадратов всех таких отклонений, т.е. статистика для испытания имеет форму отношения. Дополнительную информацию об изменчивости можно обеспечить, включая в расчеты независимые суммы квадратов. Они будут основаны на v степенях свободы и будут иметь ту же дисперсию генеральной совокупности, что и дисперсия серии данных, о которых идет речь.
В таблице В.3 приведены обозначения, которые требуются для применения испытания по критерию Хокинса к отдельным пробам.
Таблица В.3
|
Значения для пробы |
||||
|
1 |
2 |
j |
S |
|
|
Число ячеек |
n1 |
n2 |
nj |
nS |
|
Среднее значение по пробе |
m1 |
m2 |
mj |
mS |
|
Сумма квадратов |
SS1 |
SS2 |
SSj |
SSS |
|
Обозначения: |
||||
|
nj - число ячеек по j-й пробе, которые содержат не менее одного незабракованного результата; |
||||
|
mj - среднее значение по j-й пробе; |
||||
|
SSj - сумма квадратов отклонений средних
значений по ячейкам аij/ nij
относительно среднего значения по пробе mj, выраженная формулой |
||||
Выражение (L - 1) представляет число степеней свободы дисперсии средних значений по ячейкам. Значение (L - 1) следует уменьшать на единицу для каждой ячейки по j-й пробе, которая не содержит результат испытания.
Процедура испытания состоит в следующем:
а) определяют пробу k и среднее значение по ячейке аik/nik, которое имеет наибольшее экстремальное абсолютное отклонение |тk - аik/nik|. Опознанная таким образом ячейка становится кандидатом в испытании на выявление аномального значения независимо от того, является ли отклонение самым большим или самым малым;
б) рассчитывают общую сумму квадратов отклонений
![]() ; (В.7)
; (В.7)
в) рассчитывают экспериментальное значение отношения
![]() ; (B.8)
; (B.8)
г) сравнивают экспериментальное значение отношения с критическим значением из таблицы Г.4 в приложении Г для n = nk и числа степеней свободы v, дополнительного к nk
![]() , j ¹ k; (B.9)
, j ¹ k; (B.9)
д) если В* превышает критическое значение, то отбрасывают результаты, принадлежащие рассматриваемой ячейке (проба k, лаборатория i). Затем значения пk, тk и SSk пересчитывают соответствующим образом и процедуру испытания повторяют, начиная с перечисления а).
Примечание - Теоретически испытание по Хокинсу применяют для обнаружения только одной выпадающей лаборатории по какой-либо пробе. Методика повторных испытаний для единичного аномального результата, начиная с максимального отклонения от среднего по пробе, подразумевает, что критические значения в таблице Г.4 не будут точно соответствовать 1 %-ному уровню значимости. Тем не менее, как было показано Хокинсом, если п ³ 5 и общее число степеней свободы (п + v) превышает 20, то этот эффект становится пренебрежимо малым, так как выявляются эффекты маскировки (один аномальный результат скрывает другой) и «завала» (отбрасывание одного аномального результата ведет к отбрасыванию других).
В.3.2 Если испытание применяют к лабораториям, результаты которых усреднены по всем пробам, таблицу В.3 сокращают до одной колонки, содержащей
n = число лабораторий = L;
m = общее среднее = T/N,
где N - общее число результатов в таблице;
SS = сумма квадратов отклонений лабораторных средних от общего среднего, выражают формулой
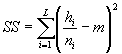 , (B.10)
, (B.10)
где ni - число результатов в i-й лаборатории.
Таким образом, с помощью такой процедуры определяют лабораторное среднее hi/ni, которое больше всего отличается от общего среднего m. В этом случае соответствующее отношение для испытания принимает вид
![]() . (B.11)
. (B.11)
Как указано выше, экспериментальное значение следует сравнить с критическим значением из таблицы Г.4, причем в этом случае дополнительные числа степеней свободы v¢ = 0. Если лабораторию отбрасывают как выпадающую, то значения n, m и SS пересчитывают соответствующим образом и повторяют вычисления.
В.4 Испытание отношения дисперсий (F-испытание)
Оценку дисперсии V1, основанную на v1 степенях свободы, можно сравнивать со второй оценкой V2 основанной на v2 степенях свободы, путем вычисления отношения
![]() . (В.12)
. (В.12)
Если экспериментальное значение отношения превышает соответствующее критическое значение, приведенное в таблицах Г.6.1 - Г.6.4, где v1 относится к числителю (к наибольшей из оценок дисперсии), a v2 относится к знаменателю, то V1 значительно превышает V2 на выбранном уровне значимости.
ПРИЛОЖЕНИЕ Г
(обязательное)
Примеры представления результатов испытаний по определению бромного числа и
статистические таблицы
В таблицах Г.1 и Г.2 представлены примеры представления результатов испытаний по определению бромного числа.
В таблицах Г.3 - Г.7 представлены критические значения, используемые при обработке результатов измерений.
Таблица Г.1 - Бромное число для низкокипящих проб
|
Бромное число для пробы |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
А |
1,9 |
64,5 |
0,80 |
3,7 |
11,0 |
46,1 |
114,8 |
1,2 |
|
2,1 |
65,5 |
0,78 |
3,8 |
11,1 |
46,5 |
114,2 |
1,2 |
|
|
В |
1,7 |
65,4 |
0,69 |
3,7 |
11,1 |
50,3 |
114,5 |
1,2 |
|
1,8 |
66,0 |
0,72 |
3,7 |
11,0 |
49,9 |
114,3 |
1,2 |
|
|
С |
1,8 |
63,5 |
0,76 |
3,5 |
10,4 |
48,5 |
112,4 |
1,3 |
|
1,8 |
63,8 |
0,76 |
3,5 |
10,5 |
48,2 |
112,7 |
1,3 |
|
|
D |
4,1 |
63,6 |
0,80 |
4,0 |
10,8 |
49,6 |
108,8 |
1,0 |
|
4,0 |
63,9 |
0,80 |
3,9 |
10,8 |
49,9 |
108,2 |
1,1 |
|
|
Е |
2,1 |
63,9 |
0,83 |
3,7 |
10,9 |
47,4 |
115,6 |
1,3 |
|
1,8 |
63,7 |
0,83 |
3,7 |
11,1 |
47,6 |
115,1 |
1,4 |
|
|
F |
1,8 |
70,7 |
0,72 |
3,4 |
11,5 |
49,1 |
121,0 |
1,4 |
|
1,7 |
69,7 |
0,64 |
3,6 |
11,2 |
47,9 |
117,9 |
1,4 |
|
|
G |
1,9 |
63,8 |
0,77 |
3,5 |
10,6 |
46,1 |
114,1 |
1,1 |
|
2,2 |
63,6 |
0,59 |
3,5 |
10,6 |
45,5 |
112,8 |
0,93 |
|
|
Н |
2,0 |
66,5 |
0,78 |
3,2 |
10,7 |
49,6 |
114,8 |
1,1 |
|
1,8 |
65,5 |
0,71 |
3,5 |
10,7 |
48,5 |
114,5 |
1,0 |
|
|
J |
2,1 |
68,2 |
0,81 |
4,0 |
11,1 |
49,1 |
115,7 |
1,4 |
|
2,1 |
65,3 |
0,81 |
3,7 |
11,1 |
47,9 |
113,9 |
1,4 |
|
Таблица Г.2 - Кубический корень из бромного числа для низкокипящих проб
|
Значение для пробы |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
А |
1,239 |
4,010 |
0,928 |
1,547 |
2,224 |
3,586 |
4,860 |
1,063 |
|
1,281 |
4,031 |
0,921 |
1,560 |
2,231 |
3,596 |
4,852 |
1,063 |
|
|
В |
1,193 |
4,029 |
0,884 |
1,547 |
2,231 |
3,691 |
4,856 |
1,063 |
|
1,216 |
4,041 |
0,896 |
1,547 |
2,224 |
3,682 |
4,853 |
1,063 |
|
|
С |
1,216 |
3,990 |
0,913 |
1,518 |
2,183 |
3,647 |
4,826 |
1,091 |
|
1,216 |
3,996 |
0,913 |
1,518 |
2,190 |
3,639 |
4,830 |
1,091 |
|
|
D |
1,601 |
3,992 |
0,928 |
1,587 |
2,210 |
3,674 |
4,774 |
1,000 |
|
1,587 |
3,998 |
0,928 |
1,574 |
2,210 |
3,682 |
4,765 |
1,032 |
|
|
Е |
1,281 |
3,998 |
0,940 |
1,547 |
2,217 |
3,619 |
4,871 |
1,091 |
|
1,216 |
3,994 |
0,940 |
1,547 |
2,231 |
3,624 |
4,864 |
1,119 |
|
|
F |
1,216 |
4,135 |
0,896 |
1,504 |
2,257 |
3,662 |
4,946 |
1,119 |
|
1,193 |
4,115 |
0,862 |
1,533 |
2,237 |
3,632 |
4,903 |
1,119 |
|
|
G |
1,239 |
3,996 |
0,917 |
1,518 |
2,197 |
3,586 |
4,850 |
1,032 |
|
1,301 |
3,992 |
0,839 |
1,518 |
2,197 |
3,570 |
4,832 |
0,976 |
|
|
Н |
1,260 |
4,051 |
0,921 |
1,474 |
2,204 |
3,674 |
4,860 |
1,032 |
|
1,216 |
4,031 |
0,892 |
1,518 |
2,204 |
3,647 |
4,856 |
1,000 |
|
|
J |
1,281 |
4,086 |
0,932 |
1,587 |
2,231 |
3,662 |
4,873 |
1,119 |
|
1,281 |
4,027 |
0,932 |
1,547 |
2,231 |
3,632 |
4,847 |
1,119 |
|
Таблица Г.3 - Критические значения критерия Кохрена для 1 %-ного уровня значимости для n оценок дисперсий и v степеней свободы
|
Критическое значение критерия Кохрена при числе степеней свободы v |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
10 |
15 |
20 |
30 |
50 |
|
|
3 |
0,9933 |
0,9423 |
0,8831 |
0,8335 |
0,7933 |
0,6743 |
0,6145 |
0,5775 |
0,5327 |
0,4872 |
|
4 |
0,9676 |
0,8643 |
0,7814 |
0,7212 |
0,6761 |
0,5536 |
0,4964 |
0,4620 |
0,4213 |
0,3808 |
|
5 |
0,9279 |
0,7885 |
0,6957 |
0,6329 |
0,5875 |
0,4697 |
0,4168 |
0,3855 |
0,3489 |
0,3131 |
|
6 |
0,8828 |
0,7218 |
0,6258 |
0,5635 |
0,5195 |
0,4084 |
0,3597 |
0,3312 |
0,2982 |
0,2661 |
|
7 |
0,8376 |
0,6644 |
0,5685 |
0,5080 |
0,4659 |
0,3616 |
0,3167 |
0,2907 |
0,2606 |
0,2316 |
|
8 |
0,7945 |
0,6152 |
0,5209 |
0,4627 |
0,4227 |
0,3248 |
0,2832 |
0,2592 |
0,2316 |
0,2052 |
|
9 |
0,7544 |
0,5727 |
0,4810 |
0,4251 |
0,3870 |
0,2950 |
0,2563 |
0,2340 |
0,2086 |
0,1842 |
|
10 |
0,7175 |
0,5358 |
0,4469 |
0,3934 |
0,3572 |
0,2704 |
0,2342 |
0,2135 |
0,1898 |
0,1673 |
|
11 |
0,6837 |
0,5036 |
0,4175 |
0,3663 |
0,3318 |
0,2497 |
0,2157 |
0,1963 |
0,1742 |
0,1532 |
|
12 |
0,6528 |
0,4751 |
0,3919 |
0,3428 |
0,3099 |
0,2321 |
0,2000 |
0,1818 |
0,1611 |
0,1414 |
|
13 |
0,6245 |
0,4498 |
0,3695 |
0,3223 |
0,2909 |
0,2169 |
0,1865 |
0,1693 |
0,1498 |
0,1313 |
|
14 |
0,5985 |
0,4272 |
0,3495 |
0,3043 |
0,2741 |
0,2036 |
0,1748 |
0,1585 |
0,1400 |
0,1226 |
|
15 |
0,5747 |
0,4069 |
0,3318 |
0,2882 |
0,2593 |
0,1919 |
0,1645 |
0,1490 |
0,1315 |
0,1150 |
|
20 |
0,4799 |
0,3297 |
0,2654 |
0,2288 |
0,2048 |
0,1496 |
0,1274 |
0,1150 |
0,1010 |
0,0879 |
|
25 |
0,4130 |
0,2782 |
0,2220 |
0,1904 |
0,1699 |
0,1230 |
0,1043 |
0,0939 |
0,0822 |
0,0713 |
|
30 |
0,3632 |
0,2412 |
0,1914 |
0,1635 |
0,1455 |
0,1046 |
0,0885 |
0,0794 |
0,0694 |
0,0600 |
|
35 |
0,3247 |
0,2134 |
0,1685 |
0,1435 |
0,1274 |
0,0912 |
0,0769 |
0,0690 |
0,0601 |
0,0519 |
|
40 |
0,2940 |
0,1916 |
0,1507 |
0,1281 |
0,1136 |
0,0809 |
0,0681 |
0,0610 |
0,0531 |
0,0457 |
|
45 |
0,2690 |
0,1740 |
0,1364 |
0,1158 |
0,1025 |
0,0727 |
0,0611 |
0,0547 |
0,0475 |
0,0409 |
|
50 |
0,2481 |
0,1596 |
0,1248 |
0,1057 |
0,0935 |
0,0661 |
0,0555 |
0,0496 |
0,0431 |
0,0370 |
|
60 |
0,2151 |
0,1371 |
0,1068 |
0,0902 |
0,0796 |
0,0561 |
0,0469 |
0,0419 |
0,0363 |
0,0311 |
|
70 |
0,1903 |
0,1204 |
0,0935 |
0,0788 |
0,0695 |
0,0487 |
0,0407 |
0,0363 |
0,0314 |
0,0269 |
|
80 |
0,1709 |
0,1075 |
0,0832 |
0,0701 |
0,0617 |
0,0431 |
0,0360 |
0,0320 |
0,0277 |
0,0236 |
|
90 |
0,1553 |
0,0972 |
0,0751 |
0,0631 |
0,0555 |
0,0387 |
0,0322 |
0,0287 |
0,0248 |
0,0211 |
|
100 |
0,1424 |
0,0888 |
0,0685 |
0,0575 |
0,0505 |
0,0351 |
0,0292 |
0,0260 |
0,0224 |
0,0191 |
Эти значения представляют осторожные аппроксимации, рассчитанные с помощью неравенства Бонферрони [4] как верхняя 0,01/n фракталь бета - распределения. Промежуточные значения в колонке для n оценок дисперсии могут быть получены с помощью линейной интерполяции обратных величин табулированных значений. Промежуточные значения для степеней свободы v могут быть получены с помощью интерполяции второго порядка (квадратической) для обратных величин табулированных значений.
Таблица Г.4 - Критические значения, используемые для выявления аномальных результатов при испытании по Хокинсу для v = (0¸200) и n = (3¸50)
|
Критическое значение при числе степеней свободы v |
||||||||||||
|
0 |
5 |
10 |
15 |
20 |
30 |
40 |
50 |
70 |
100 |
150 |
200 |
|
|
3 |
0,8165 |
0,7240 |
0,6100 |
0,5328 |
0,4781 |
0,4049 |
0,3574 |
0,3233 |
0,2769 |
0,2340 |
0,1926 |
0,1674 |
|
4 |
0,8639 |
0,7505 |
0,6405 |
0,5644 |
0,5094 |
0,4345 |
0,3850 |
0,3492 |
0,3000 |
0,2541 |
0,2096 |
0,1824 |
|
5 |
0,8818 |
0,7573 |
0,6530 |
0,5796 |
0,5258 |
0,4510 |
0,4012 |
0,3647 |
0,3142 |
0,2668 |
0,2204 |
0,1920 |
|
6 |
0,8823 |
0,7554 |
0,6547 |
0,5869 |
0,5347 |
0,4612 |
0,4115 |
0,3749 |
0,3238 |
0,2755 |
0,2280 |
0,1988 |
|
7 |
0,8733 |
0,7493 |
0,6567 |
0,5898 |
0,5394 |
0,4676 |
0,4184 |
0,3819 |
0,3307 |
0,2819 |
0,2337 |
0,2039 |
|
8 |
0,8596 |
0,7409 |
0,6538 |
0,5901 |
0,5415 |
0,4715 |
0,4231 |
0,3869 |
0,3358 |
0,2868 |
0,2381 |
0,2079 |
|
9 |
0,8439 |
0,7314 |
0,6493 |
0,5886 |
0,5418 |
0,4738 |
0,4262 |
0,3905 |
0,3396 |
0,2906 |
0,2416 |
0,2112 |
|
10 |
0,8274 |
0,7213 |
0,6439 |
0,5861 |
0,5411 |
0,4750 |
0,4283 |
0,3930 |
0,3426 |
0,2936 |
0,2445 |
0,2139 |
|
11 |
0,8108 |
0,7111 |
0,6380 |
0,5828 |
0,5394 |
0,4753 |
0,4295 |
0,3948 |
0,3448 |
0,2961 |
0,2469 |
0,2162 |
|
12 |
0,7947 |
0,7010 |
0,6318 |
0,5790 |
0,5373 |
0,4750 |
0,4302 |
0,3960 |
0,3466 |
0,2981 |
0,2489 |
0,2181 |
|
13 |
0,7791 |
0,6910 |
0,6254 |
0,5749 |
0,5347 |
0,4742 |
0,4304 |
0,3968 |
0,3479 |
0,2997 |
0,2507 |
0,2198 |
|
14 |
0,7642 |
0,6812 |
0,6189 |
0,5706 |
0,5319 |
0,4731 |
0,4302 |
0,3972 |
0,3489 |
0,3011 |
0,2521 |
0,2212 |
|
15 |
0,7500 |
0,6717 |
0,6125 |
0,5662 |
0,5288 |
0,4717 |
0,4298 |
0,3973 |
0,3496 |
0,3021 |
0,2534 |
0,2225 |
|
16 |
0,7364 |
0,6625 |
0,6061 |
0,5617 |
0,5256 |
0,4701 |
0,4291 |
0,3972 |
0,3501 |
0,3030 |
0,2544 |
0,2236 |
|
17 |
0,7235 |
0,6535 |
0,5998 |
0,5571 |
0,5223 |
0,4683 |
0,4282 |
0,3968 |
0,3504 |
0,3037 |
0,2554 |
0,2246 |
|
18 |
0,7112 |
0,6449 |
0,5936 |
0,5526 |
0,5189 |
0,4665 |
0,4272 |
0,3964 |
0,3505 |
0,3043 |
0,2562 |
0,2254 |
|
19 |
0,6996 |
0,6365 |
0,5876 |
0,5480 |
0,5155 |
0,4645 |
0,4260 |
0,3958 |
0,3506 |
0,3047 |
0,2569 |
0,2262 |
|
20 |
0,6884 |
0,6286 |
0,5816 |
0,5436 |
0,5120 |
0,4624 |
0,4248 |
0,3951 |
0,3505 |
0,3051 |
0,2575 |
0,2269 |
|
21 |
0,6778 |
0,6209 |
0,5758 |
0,5392 |
0,5086 |
0,4603 |
0,4235 |
0,3942 |
0,3503 |
0,3053 |
0,2580 |
0,2275 |
|
22 |
0,6677 |
0,6134 |
0,5702 |
0,5348 |
0,5052 |
0,4581 |
0,4221 |
0,3934 |
0,3500 |
0,3055 |
0,2584 |
0,2280 |
|
23 |
0,6581 |
0,6062 |
0,5647 |
0,5305 |
0,5018 |
0,4559 |
0,4206 |
0,3924 |
0,3496 |
0,3056 |
0,2588 |
0,2285 |
|
24 |
0,6488 |
0,5993 |
0,5593 |
0,5263 |
0,4984 |
0,4537 |
0,4191 |
0,3914 |
0,3492 |
0,3056 |
0,2591 |
0,2289 |
|
25 |
0,6400 |
0,5925 |
0,5540 |
0,5221 |
0,4951 |
0,4515 |
0,4176 |
0,3904 |
0,3488 |
0,3056 |
0,2594 |
0,2293 |
|
26 |
0,6315 |
0,5861 |
0,5490 |
0,5180 |
0,4918 |
0,4492 |
0,4160 |
0,3893 |
0,3482 |
0,3054 |
0,2596 |
0,2296 |
|
27 |
0,6234 |
0,5798 |
0,5440 |
0,5140 |
0,4885 |
0,4470 |
0,4145 |
0,3881 |
0,3477 |
0,3053 |
0,2597 |
0,2299 |
|
28 |
0,6156 |
0,5737 |
0,5392 |
0,5101 |
0,4853 |
0,4447 |
0,4129 |
0,3870 |
0,3471 |
0,3051 |
0,2599 |
0,2302 |
|
29 |
0,6081 |
0,5678 |
0,5345 |
0,5063 |
0,4821 |
0,4425 |
0,4113 |
0,3858 |
0,3464 |
0,3049 |
0,2600 |
0,2304 |
|
30 |
0,6009 |
0,5621 |
0,5299 |
0,5025 |
0,4790 |
0,4403 |
0,4097 |
0,3846 |
0,3458 |
0,3047 |
0,2600 |
0,2306 |
|
35 |
0,5686 |
0,5361 |
0,5086 |
0,4848 |
0,4641 |
0,4294 |
0,4016 |
0,3785 |
0,3421 |
0,3031 |
0,2600 |
0,2312 |
|
40 |
0,5413 |
0,5136 |
0,4897 |
0,4688 |
0,4504 |
0,4191 |
0,3936 |
0,3722 |
0,3382 |
0,3010 |
0,2594 |
0,2314 |
|
45 |
0,5179 |
0,4939 |
0,4728 |
0,4542 |
0,4377 |
0,4094 |
0,3859 |
0,3660 |
0,3340 |
0,2987 |
0,2586 |
0,2312 |
|
50 |
0,4975 |
0,4764 |
0,4577 |
0,4410 |
0,4260 |
0,4002 |
0,3785 |
0,3600 |
0,3299 |
0,2962 |
0,2575 |
0,2308 |
Критические значения в таблице откорректированы до четвертого десятичного знака в диапазоне значений n = (3¸30) и v = 0; 5; 15 и 30 [4]. Другие значения выведены с помощью неравенства Бонферрони
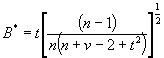 , (Г.1)
, (Г.1)
где t является верхней 0,005/n фрактилью переменной t с n + v - 2 степенями свободы. Рассчитанные таким образом значения являются довольно осторожными оценками с максимальной ошибкой относительно истинного значения около 0,0002. Промежуточные значения для n и v могут быть получены с помощью интерполяции второго порядка, использующей квадрат обратных величин табулированных значений. Подобным образом экстраполяция второго порядка может быть использована для оценки значений, превосходящих n = 50 и v = 200.
Таблица Г.5 - Критические значения для t-критерия Стьюдента
|
Критические значения при уровне значимости при двусторонней постановке задачи, % |
|||||||
|
50 |
40 |
30 |
20 |
10 |
5 |
1 |
|
|
1 |
1,000 |
1,376 |
1,963 |
3,078 |
6,314 |
12,706 |
63,657 |
|
2 |
0,816 |
1,061 |
1,386 |
1,886 |
2,920 |
4,303 |
9,925 |
|
3 |
0,765 |
0,978 |
1,250 |
1,638 |
2,353 |
3,182 |
5,841 |
|
4 |
0,741 |
0,941 |
1,190 |
1,533 |
2,132 |
2,776 |
4,604 |
|
5 |
0,727 |
0,920 |
1,156 |
1,476 |
2,015 |
2,571 |
4,032 |
|
6 |
0,718 |
0,906 |
1,134 |
1,440 |
1,943 |
2,447 |
3,707 |
|
7 |
0,711 |
0,896 |
1,119 |
1,415 |
1,895 |
2,365 |
3,499 |
|
8 |
0,706 |
0,889 |
1,108 |
1,397 |
1,860 |
2,306 |
3,355 |
|
9 |
0,703 |
0,883 |
1,100 |
1,383 |
1,833 |
2,262 |
3,250 |
|
10 |
0,700 |
0,879 |
1,093 |
1,372 |
1,812 |
2,228 |
3,165 |
|
11 |
0,697 |
0,876 |
1,088 |
1,363 |
1,796 |
2,201 |
3,106 |
|
12 |
0,695 |
0,873 |
1,083 |
1,356 |
1,782 |
2,179 |
3,055 |
|
13 |
0,694 |
0,870 |
1,079 |
1,350 |
1,771 |
2,160 |
3,012 |
|
14 |
0,692 |
0,868 |
1,076 |
1,345 |
1,761 |
2,145 |
2,977 |
|
15 |
0,691 |
0,866 |
1,074 |
1,341 |
1,753 |
2,131 |
2,947 |
|
16 |
0,690 |
0,865 |
1,071 |
1,337 |
1,746 |
2,120 |
2,921 |
|
17 |
0,689 |
0,863 |
1,069 |
1,333 |
1,740 |
2,110 |
2,898 |
|
18 |
0,688 |
0,862 |
1,067 |
1,330 |
1,734 |
2,101 |
2,878 |
|
19 |
0,688 |
0,861 |
1,066 |
1,328 |
1,729 |
2,093 |
2,861 |
|
20 |
0,687 |
0,860 |
1,064 |
1,325 |
1,725 |
2,086 |
2,845 |
|
21 |
0,686 |
0,859 |
1,063 |
1,323 |
1,721 |
2,080 |
2,831 |
|
22 |
0,686 |
0,858 |
1,061 |
1,321 |
1,717 |
2,074 |
2,819 |
|
23 |
0,685 |
0,858 |
1,060 |
1,319 |
1,714 |
2,069 |
2,807 |
|
24 |
0,685 |
0,857 |
1,059 |
1,318 |
1,711 |
2,064 |
2,797 |
|
25 |
0,684 |
0,856 |
1,058 |
1,316 |
1,708 |
2,060 |
2,787 |
|
26 |
0,684 |
0,856 |
1,058 |
1,315 |
1,706 |
2,056 |
2,779 |
|
27 |
0,684 |
0,855 |
1,057 |
1,314 |
1,703 |
2,052 |
2,771 |
|
28 |
0,683 |
0,855 |
1,056 |
1,313 |
1,701 |
2,048 |
2,763 |
|
29 |
0,683 |
0,854 |
1,055 |
1,311 |
1,699 |
2,045 |
2,756 |
|
30 |
0,683 |
0,854 |
1,055 |
1,310 |
1,697 |
2,042 |
2,750 |
|
40 |
0,681 |
0,851 |
1,050 |
1,303 |
1,684 |
2,021 |
2,704 |
|
50 |
0,680 |
0,849 |
1,048 |
1,299 |
1,676 |
2,008 |
2,678 |
|
60 |
0,679 |
0,848 |
1,046 |
1,296 |
1,671 |
2,000 |
2,660 |
|
120 |
0,677 |
0,845 |
1,041 |
1,289 |
1,658 |
1,980 |
2,617 |
|
¥ |
0,674 |
0,842 |
1,036 |
1,282 |
1,645 |
1,960 |
2,576 |
Таблица Г.6.1 - Критические значения для F-критерия Фишера на 5 %-ном уровне значимости
|
v2 |
v1 |
|||||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
30 |
50 |
100 |
200 |
500 |
¥ |
|
|
3 |
9,28 |
9,12 |
9,01 |
8,94 |
8,89 |
8,85 |
8,81 |
8,79 |
8,70 |
8,66 |
8,62 |
8,58 |
8,55 |
8,54 |
8,53 |
8,53 |
|
4 |
6,59 |
6,39 |
6,26 |
6,16 |
6,09 |
6,04 |
6,00 |
5,96 |
5,86 |
5,80 |
5,75 |
5,70 |
5,66 |
5,65 |
5,64 |
5,63 |
|
5 |
5,41 |
5,19 |
5,05 |
4,95 |
4,88 |
4,82 |
4,77 |
4,74 |
4,62 |
4,56 |
4,50 |
4,44 |
4,41 |
4,39 |
4,37 |
4,37 |
|
6 |
4,76 |
4,53 |
4,39 |
4,28 |
4,21 |
4,15 |
4,10 |
4,06 |
3,94 |
3,87 |
3,81 |
3,75 |
3,71 |
3,69 |
3,68 |
3,67 |
|
7 |
4,35 |
4,12 |
3,97 |
3,87 |
3,79 |
3,73 |
3,68 |
3,64 |
3,51 |
3,44 |
3,38 |
3,32 |
3,27 |
3,25 |
3,24 |
3,23 |
|
8 |
4,07 |
3,84 |
3,69 |
3,58 |
3,50 |
3,44 |
3,39 |
3,35 |
3,22 |
3,15 |
3,08 |
3,02 |
2,97 |
2,95 |
2,94 |
2,93 |
|
9 |
3,86 |
3,63 |
3,48 |
3,37 |
3,29 |
3,23 |
3,18 |
3,14 |
3,01 |
2,94 |
2,86 |
2,80 |
2,76 |
2,73 |
2,72 |
2,71 |
|
10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,14 |
3,07 |
3,02 |
2,98 |
2,85 |
2,77 |
2,70 |
2,64 |
2,59 |
2,56 |
2,55 |
2,54 |
|
15 |
3,29 |
3,06 |
2,90 |
2,79 |
2,71 |
2,64 |
2,59 |
2,54 |
2,40 |
2,33 |
2,25 |
2,18 |
2,12 |
2,10 |
2,08 |
2,07 |
|
20 |
3,10 |
2,87 |
2,71 |
2,60 |
2,51 |
2,45 |
2,39 |
2,35 |
2,20 |
2,12 |
2,04 |
1,97 |
1,91 |
1,88 |
1,86 |
1,84 |
|
30 |
2,92 |
2,69 |
2,53 |
2,42 |
2,33 |
2,27 |
2,21 |
2,16 |
2,01 |
1,93 |
1,84 |
1,76 |
1,70 |
1,66 |
1,64 |
1,62 |
|
50 |
2,79 |
2,56 |
2,40 |
2,29 |
2,20 |
2,13 |
2,07 |
2,03 |
1,87 |
1,78 |
1,69 |
1,60 |
1,52 |
1,48 |
1,46 |
1,44 |
|
100 |
2,70 |
2,46 |
2,31 |
2,19 |
2,10 |
2,03 |
1,97 |
1,93 |
1,77 |
1,68 |
1,57 |
1,48 |
1,39 |
1,34 |
1,31 |
1,28 |
|
200 |
2,65 |
2,42 |
2,26 |
2,14 |
2,06 |
1,98 |
1,93 |
1,88 |
1,72 |
1,62 |
1,52 |
1,41 |
1,32 |
1,26 |
1,22 |
1,19 |
|
500 |
2,62 |
2,39 |
2,23 |
2,12 |
2,03 |
1,96 |
1,90 |
1,85 |
1,69 |
1,59 |
1,48 |
1,38 |
1,28 |
1,21 |
1,16 |
1,11 |
|
¥ |
2,60 |
2,37 |
2,21 |
2,10 |
2,01 |
1,94 |
1,88 |
1,83 |
1,67 |
1,57 |
1,46 |
1,35 |
1,24 |
1,17 |
1,11 |
1,00 |
Таблица Г.6.2 - Критические значения для F-критерия Фишера на 1 %-ном уровне значимости
|
v2 |
v1 |
|||||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
30 |
50 |
100 |
200 |
500 |
¥ |
|
|
3 |
29,5 |
28,7 |
28,2 |
27,9 |
27,7 |
27,5 |
27,3 |
27,2 |
26,9 |
26,7 |
26,5 |
26,4 |
26,2 |
26,2 |
26,1 |
26,1 |
|
4 |
16,7 |
16,0 |
15,5 |
15,2 |
15,0 |
14,8 |
14,7 |
14,5 |
14,2 |
14,0 |
13,8 |
13,7 |
13,6 |
13,5 |
13,5 |
13,5 |
|
5 |
12,1 |
11,4 |
11,0 |
10,7 |
10,5 |
10,3 |
10,2 |
10,1 |
9,72 |
9,55 |
9,38 |
9,24 |
9,13 |
9,08 |
9,04 |
9,02 |
|
6 |
9,78 |
9,15 |
8,75 |
8,47 |
8,26 |
8,10 |
7,98 |
7,87 |
7,56 |
7,40 |
7,23 |
7,09 |
6,99 |
6,93 |
6,90 |
6,88 |
|
7 |
8,45 |
7,85 |
7,46 |
7,19 |
6,99 |
6,84 |
6,72 |
6,62 |
6,31 |
6,16 |
5,99 |
5,86 |
5,75 |
5,70 |
5,67 |
5,65 |
|
8 |
7,59 |
7,01 |
6,63 |
6,37 |
6,18 |
6,03 |
5,91 |
5,81 |
5,52 |
5,36 |
5,20 |
5,07 |
4,96 |
4,91 |
4,88 |
4,86 |
|
9 |
6,99 |
6,42 |
6,06 |
5,80 |
5,61 |
5,47 |
5,35 |
5,26 |
4,96 |
4,81 |
4,65 |
4,52 |
4,42 |
4,36 |
4,33 |
4,31 |
|
10 |
6,55 |
5,99 |
5,64 |
5,39 |
5,20 |
5,06 |
4,94 |
4,85 |
4,56 |
4,41 |
4,25 |
4,12 |
4,01 |
3,96 |
3,93 |
3,91 |
|
15 |
5,42 |
4,89 |
4,56 |
4,32 |
4,14 |
4,00 |
3,89 |
3,80 |
3,52 |
3,37 |
3,21 |
3,08 |
2,98 |
2,92 |
2,89 |
2,87 |
|
20 |
4,94 |
4,43 |
4,10 |
3,87 |
3,70 |
3,56 |
3,46 |
3,37 |
3,09 |
2,94 |
2,78 |
2,64 |
2,54 |
2,48 |
2,44 |
2,42 |
|
30 |
4,51 |
4,02 |
3,70 |
3,47 |
3,30 |
3,17 |
3,07 |
2,98 |
2,70 |
2,55 |
2,39 |
2,25 |
2,13 |
2,07 |
2,03 |
2,01 |
|
50 |
4,20 |
3,72 |
3,41 |
3,19 |
3,02 |
2,89 |
2,79 |
2,70 |
2,42 |
2,27 |
2,10 |
1,95 |
1,82 |
1,76 |
1,71 |
1,68 |
|
100 |
3,98 |
3,51 |
3,21 |
2,99 |
2,82 |
2,69 |
2,59 |
2,50 |
2,22 |
2,07 |
1,89 |
1,73 |
1,60 |
1,52 |
1,47 |
1,43 |
|
200 |
3,88 |
3,41 |
3,11 |
2,89 |
2,73 |
2,60 |
2,50 |
2,41 |
2,13 |
1,97 |
1,79 |
1,63 |
1,48 |
1,39 |
1,33 |
1,28 |
|
500 |
3,82 |
3,36 |
3,05 |
2,84 |
2,68 |
2,55 |
2,44 |
2,36 |
2,07 |
1,92 |
1,74 |
1,56 |
1,41 |
1,31 |
1,23 |
1,16 |
|
¥ |
3,78 |
3,32 |
3,02 |
2,80 |
2,64 |
2,51 |
2,41 |
2,32 |
2,04 |
1,88 |
1,70 |
1,52 |
1,36 |
1,25 |
1,15 |
1,00 |
|
Примечание - Источником для таблиц Г.6.1 - Г.6.4 является [9]. |
||||||||||||||||
Таблица Г.6.3 - Критические значения для F- критерия Фишера на 0,1 %-ном уровне значимости
|
v2 |
v1 |
|||||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
30 |
50 |
100 |
200 |
500 |
¥ |
|
|
3 |
141 |
137 |
135 |
133 |
132 |
131 |
130 |
129 |
127 |
126 |
125 |
125 |
124 |
124 |
124 |
124 |
|
4 |
56,2 |
53,4 |
51,7 |
50,5 |
49,7 |
49,0 |
48,5 |
48,0 |
46,8 |
46,1 |
45,4 |
44,9 |
44,5 |
44,3 |
44,1 |
44,0 |
|
5 |
33,2 |
31,1 |
29,8 |
28,8 |
28,2 |
27,6 |
27,2 |
26,9 |
25,9 |
25,4 |
24,9 |
24,4 |
24,1 |
23,9 |
23,8 |
23,8 |
|
6 |
23,7 |
21,9 |
20,8 |
20,0 |
19,5 |
19,0 |
18,7 |
18,4 |
17,6 |
17,1 |
16,7 |
16,3 |
16,0 |
15,9 |
15,8 |
15,8 |
|
7 |
18,8 |
17,2 |
16,2 |
15,5 |
15,0 |
14,6 |
14,3 |
14,1 |
13,3 |
12,9 |
12,5 |
12,2 |
11,9 |
11,8 |
11,7 |
11,7 |
|
8 |
15,8 |
14,4 |
13,5 |
12,9 |
12,4 |
12,0 |
11,8 |
11,5 |
10,8 |
10,5 |
10,1 |
9,80 |
9,57 |
9,46 |
9,39 |
9,34 |
|
9 |
13,9 |
12,6 |
11,7 |
11,1 |
10,7 |
10,4 |
10,1 |
9,89 |
9,24 |
8,90 |
8,55 |
8,26 |
8,04 |
7,93 |
7,86 |
7,81 |
|
10 |
12,6 |
11,3 |
10,5 |
9,92 |
9,52 |
9,20 |
8,96 |
8,75 |
8,13 |
7,80 |
7,47 |
7,19 |
6,98 |
6,87 |
6,81 |
6,76 |
|
15 |
9,34 |
8,25 |
7,57 |
7,09 |
6,74 |
6,47 |
6,26 |
6,08 |
5,53 |
5,25 |
4,95 |
4,70 |
4,51 |
4,41 |
4,35 |
4,31 |
|
20 |
8,10 |
7,10 |
6,46 |
6,02 |
5,69 |
5,44 |
5,24 |
5,08 |
4,56 |
4,29 |
4,01 |
3,77 |
3,58 |
3,48 |
3,42 |
3,38 |
|
30 |
7,05 |
6,12 |
5,53 |
5,12 |
4,82 |
4,58 |
4,39 |
4,24 |
3,75 |
3,49 |
3,22 |
2,98 |
2,79 |
2,69 |
2,63 |
2,59 |
|
50 |
6,34 |
5,46 |
4,90 |
4,51 |
4,22 |
4,00 |
3,82 |
3,67 |
3,20 |
2,95 |
2,68 |
2,44 |
2,24 |
2,14 |
2,07 |
2,03 |
|
100 |
5,85 |
5,01 |
4,48 |
4,11 |
3,83 |
3,61 |
3,44 |
3,30 |
2,84 |
2,59 |
2,32 |
2,07 |
1,87 |
1,75 |
1,68 |
1,62 |
|
200 |
5,64 |
4,81 |
4,29 |
3,92 |
3,65 |
3,43 |
3,26 |
3,12 |
2,67 |
2,42 |
2,15 |
1,90 |
1,68 |
1,55 |
1,46 |
1,39 |
|
500 |
5,51 |
4,69 |
4,18 |
3,82 |
3,54 |
3,33 |
3,16 |
3,02 |
2,58 |
2,33 |
2,05 |
1,80 |
1,57 |
1,43 |
1,32 |
1,23 |
|
¥ |
5,42 |
4,62 |
4,10 |
3,74 |
3,47 |
3,27 |
3,10 |
2,96 |
2,51 |
2,27 |
1,99 |
1,73 |
1,49 |
1,34 |
1,21 |
1,00 |
Таблица Г.6.4 - Критические значения для F-критерия Фишера на 0,05 %-ном уровне значимости
|
v2 |
v1 |
|||||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
30 |
50 |
100 |
200 |
500 |
¥ |
|
|
3 |
225 |
218 |
214 |
211 |
209 |
208 |
207 |
206 |
203 |
201 |
199 |
198 |
197 |
197 |
196 |
196 |
|
4 |
80,1 |
76,1 |
73,6 |
71,9 |
70,6 |
69,7 |
68,9 |
68,3 |
66,5 |
65,5 |
64,6 |
63,8 |
63,2 |
62,9 |
62,7 |
62,6 |
|
5 |
44,4 |
41,5 |
39,7 |
38,5 |
37,6 |
36,9 |
36,4 |
35,9 |
34,6 |
33,9 |
33,1 |
32,5 |
32,1 |
31,8 |
31,7 |
31,6 |
|
6 |
30,4 |
28,1 |
26,6 |
25,6 |
24,9 |
24,3 |
23,9 |
23,5 |
22,4 |
21,9 |
21,4 |
20,9 |
20,5 |
20,1 |
20,2 |
20,1 |
|
7 |
23,5 |
21,4 |
20,2 |
19,3 |
18,7 |
18,2 |
17,8 |
17,5 |
16,5 |
16,0 |
15,5 |
15,1 |
14,7 |
14,6 |
14,5 |
14,4 |
|
8 |
19,4 |
17,6 |
16,4 |
15,7 |
15,1 |
14,6 |
14,3 |
14,0 |
13,1 |
12,7 |
12,2 |
11,8 |
11,6 |
11,4 |
11,4 |
11,3 |
|
9 |
16,8 |
15,1 |
14,1 |
13,3 |
12,8 |
12,4 |
12,1 |
11,8 |
11,0 |
10,6 |
10,2 |
9,80 |
9,53 |
9,40 |
9,32 |
9,26 |
|
10 |
15,0 |
13,4 |
12,4 |
11,8 |
11,3 |
10,9 |
10,6 |
10,3 |
9,56 |
9,16 |
8,75 |
8,42 |
8,16 |
8,04 |
7,96 |
7,90 |
|
15 |
10,8 |
9,48 |
8,66 |
8,10 |
7,68 |
7,36 |
7,11 |
6,91 |
6,27 |
5,93 |
5,58 |
5,29 |
5,06 |
4,94 |
4,87 |
4,83 |
|
20 |
9,20 |
8,02 |
7,28 |
6,76 |
6,38 |
6,08 |
5,85 |
5,66 |
5,07 |
4,75 |
4,42 |
4,15 |
3,93 |
3,82 |
3,75 |
3,70 |
|
30 |
7,90 |
6,82 |
6,14 |
5,66 |
5,31 |
5,04 |
4,82 |
4,65 |
4,10 |
3,80 |
3,48 |
3,22 |
3,00 |
2,89 |
2,82 |
2,78 |
|
50 |
7,01 |
6,01 |
5,37 |
4,93 |
4,60 |
4,34 |
4,14 |
3,98 |
3,45 |
3,16 |
2,86 |
2,59 |
2,37 |
2,25 |
2,17 |
2,13 |
|
100 |
6,43 |
5,47 |
4,87 |
4,44 |
4,13 |
3,89 |
3,70 |
3,54 |
3,03 |
2,75 |
2,44 |
2,18 |
1,95 |
1,82 |
1,74 |
1,67 |
|
200 |
6,16 |
5,23 |
4,64 |
4,23 |
3,92 |
3,68 |
3,49 |
3,34 |
2,83 |
2,56 |
2,25 |
1,98 |
1,74 |
1,60 |
1,50 |
1,42 |
|
500 |
6,01 |
5,09 |
4,51 |
4,10 |
3,80 |
3,56 |
3,36 |
3,21 |
2,72 |
2,45 |
2,14 |
1,87 |
1,61 |
1,46 |
1,34 |
1,24 |
|
¥ |
5,91 |
5,00 |
4,42 |
4,02 |
3,72 |
3,48 |
3,30 |
3,14 |
2,65 |
2,37 |
2,07 |
1,79 |
1,53 |
1,36 |
1,22 |
1,00 |
Критические значения для F-критерия, не вошедшие в таблицу, могут быть приближенно рассчитаны с помощью интерполяции второго порядка (квадратической) табличных значений.
Критические значения F-критерия, соответствующие v1 > 30 и v2 > 30 степеней свободы и уровню значимости 100 (1 - Р) %, где Р - доверительная вероятность, также могут быть приближенно рассчитаны по формуле
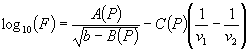 , (Г.2)
, (Г.2)
где 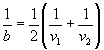 .
.
Значения A(P), B(P) и С(P) для типичных значений уровня значимости 100(1 - P) % приведены в таблице Г.6.5.
Таблица Г.6.5
|
А(Р) |
В(Р) |
С(Р) |
|
|
10 |
1,1131 |
0,77 |
0,527 |
|
5 |
1,4287 |
0,95 |
0,681 |
|
2,5 |
1,7023 |
1,14 |
0,846 |
|
1,0 |
2,0206 |
1,40 |
1,073 |
|
0,5 |
2,2373 |
1,61 |
1,250 |
|
0,1 |
2,6841 |
2,09 |
1,672 |
|
0,05 |
2,8580 |
2,30 |
1,857 |
Для не вошедших в таблицу значений доверительной вероятности Р критические значения F-критерия могут быть получены с помощью квадратической (второго порядка) интерполяции/экстраполяции log(F) (либо табулированных, либо оцененных по формуле) в зависимости от log (1 - Р).
Критические значения ординат нормированного нормального распределения приведены в таблице Г.7.
Таблица Г.7
|
0,70 |
0,80 |
0,90 |
0,95 |
0,975 |
0,99 |
0,995 |
|
|
Z |
0,524 |
0,842 |
1,282 |
1,645 |
1,960 |
2,326 |
2,576 |
|
2 (1 - Р) |
0,60 |
0,40 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
Критические значения Z, соответствующие доверительной вероятности Р при односторонней постановке задачи или доверительной вероятности (уровню значимости) 2 (1 - Р) при двусторонней постановке задачи, приведены в терминах «нормированной нормальной переменной»
![]() , (Г.3)
, (Г.3)
где m и s - параметры нормального распределения - среднее и стандартное отклонение соответственно.
Если Р становится меньше 0,5, подходящее критическое значение становится отрицательным, соответствующим доверительной вероятности (1 - Р).
ПРИЛОЖЕНИЕ Д
(обязательное)
Виды зависимостей и подходящие преобразования (см. 4.1)
Виды зависимостей приведены в таблице Д.1.
Таблица Д.1
|
Преобразование |
Линейная зависимость в виде, который используется для подгонки |
dx/dy |
Примечание |
||
|
1. D = K(m + В) |
у = log (x + В) «логарифмическое» |
log(D) = b0 + b1log(m + В) + b2T + b3Tlog(m + В) |
(x+B) |
Меры предосторожности должны быть приняты при малых значениях (x + В), так как влияние округления становится существенным |
|
|
Испытание: b1 = 1 |
|||||
|
0 < m + В |
|||||
|
2. D = KmB |
y=x1-B |
log(D) = b0 + b1log(m) + b2T + b3Tlog(m) |
xB (1 - B) |
Линия подгонки будет проходить через начало координат. Общим случаем является ситуация, когда B = 1/2 или 2 |
|
|
B ¹ 1 |
«степенное» |
||||
|
Испытание: b1 ¹ 0 |
|||||
|
3.
|
|
log(D) = b0 + b1log[m (В - m)] + b2T + b3Tlog[m (В - m)] |
|
Этот случай часто
возникает, когда результаты сообщают как проценты или качественно как «счет».
При малых значениях «x» во всем диапазоне преобразование
трансформируют к виду |
|
|
Испытание: b1 = 1/2 |
|||||
|
типа «arcsin» |
|||||
|
0 £ m £ B |
|||||
|
4. |
|
log(D) = b0 + b1log[m (В - m)] + b2T + b3Tlog[m (В - m)] |
x (B - x) В |
Этот случай возникает, когда сообщенные результаты оценены по балльной шкале от 0 до В. При малых значениях «x» во всем диапазоне преобразование трансформируют к виду у = log (x), специальному случаю пункта 1, приведенному выше |
|
|
Испытание: b1 = 1 |
|||||
|
0 £ m £ B |
|||||
|
типа «logistic» |
|||||
|
5. |
|
log(D) = b0 + b1log(m2 +В2) + b2T + b3Tlog(m2 +В2) |
(x2 + B2) В |
Линия подгонки не проходит через начало координат. При малых значениях В преобразование трансформируют к виду у = 1/х, специальному случаю пункта 2, приведенному выше |
|
|
Испытание: b1 = 1 |
|||||
|
типа «arctan» |
|||||
|
В > 0 |
Приведенные выше виды зависимостей представлены графически на рисунках Д.1 - Д.5. Во всех случаях К - произвольная положительная постоянная. Уравнение зависимости, которое используют для подгонки, включает фиктивную переменную T (формула E.1), с помощью которой возможно проверить, различаются ли значимо примененные для повторяемости (сходимости) и воспроизводимости преобразования.
Д.1 Процедура выполнения преобразования
Процедура установления правильного типа преобразования и его параметра В должна включать следующие этапы:
а) построение графика зависимости лабораторных стандартных отклонений D и стандартных отклонений для повторных испытаний d от средних по пробам (т) в виде диаграмм рассеяния и выбор зависимости (рисунки Д.1 - Д.5);
б) оценки параметра преобразования В по диаграммам рассеяния за исключением степенного преобразования (вид 2 в таблице Д.1). Для преобразований вида «arcsin» (вид 3) и «logistic» (вид 4) этот параметр будет известен, так как в обоих случаях В - верхний предел либо шкалы в баллах, либо «счета», в терминах которых определены результаты. Для логарифмического преобразования (вид 1) рассчитывают В по отрезку, отсекаемому на ординате, и наклону прямой, оцененной по диаграммам рассеяния. Подобным образом оценивают В по отрезку, отсекаемому на ординате, в случае преобразования вида «arctan» (вид 5). В любом случае В следует округлить так, чтобы получить значение, которое удовлетворяет графикам для лабораторных стандартных отклонений и стандартных отклонений для повторных испытаний;
в) в соответствии с расчетной процедурой по приложению Е.3 осуществляют подгонку под определенную линию в таблице Д.1 для выбранного преобразования. Коэффициент b1 для степенного преобразования должен значимо отличаться от нуля и обеспечивать оценку В, которую округляют до разумного значения. Коэффициент b1 для преобразования вида «arcsin» не должен значимо отличаться от 0,5. Подобным образом b1 для преобразований вида «logistic», «log» и «arctan» не должен значимо отличаться от единицы. В каждом случае испытание, установленное в таблице Д.1, необходимо применять на 5 %-ном уровне значимости. Попадание результата испытаний в критическую область означает, что либо некорректен выбор типа преобразования, либо некорректна оценка параметра В. Подобным образом коэффициент b3 в каждом случае должен быть проверен оценкой нуля. Отрицательный результат в этом случае означает, что преобразования для повторяемости (сходимости) и для воспроизводимости различаются. В некоторых случаях наличие аномальных результатов по 4.2 может вызывать такое различие;
г) если испытания, примененные выше, дали положительные результаты, проводят соответствующим образом преобразование всех результатов, пересчитывают средние и стандартные отклонения, используя преобразованные результаты, и строят новые диаграммы рассеяния, как предложено в пункте а). Теперь эти диаграммы показывают постоянный уровень для лабораторного стандартного отклонения и постоянный уровень (но необязательно тот же самый) для стандартного отклонения по повторным испытаниям. Процедура испытания однородности приведена в 4.3.
Диаграммы рассеяния
D = К (m + В), (т + В) > 0
Рисунок Д.1
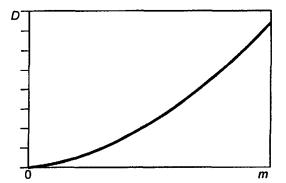
D = Кm2, В > 1
Рисунок Д.2.1
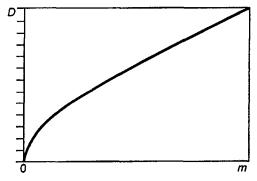
D = Кm2, 0 < В < 1
Рисунок Д.2.2
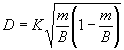 , 0 £ m £ B
, 0 £ m £ B
Рисунок Д.3
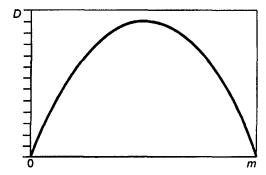
![]() , 0 £ m £ B
, 0 £ m £ B
Рисунок Д.4
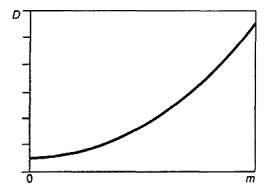
![]() , B > 0
, B > 0
Рисунок Д.5
ПРИЛОЖЕНИЕ Е
(обязательное)
Метод взвешенного линейного регрессионного анализа (см. 4.1.3)
E.1 Пояснение для применения фиктивной переменной
Е.1.1 В общем случае две различные переменные Y1 и Y2 при построении графика зависимости относительно одной и той же независимой переменной Х будут давать различные зависимости:
Y1 = b10 + b11X,
Y2 = b20 + b21X, (E.1)
где коэффициенты bij оценивают с помощью регрессионного анализа. Для того, чтобы сравнить две зависимости, фиктивная переменная Т может быть определена таким образом, что:
Т = T1 - постоянная величина для каждого наблюдения Y1,
Т = T2 - постоянная величина для каждого наблюдения Y2 и
T1 ¹ T2.
E.1.2 Допуская, что Y представляет комбинацию Y1 и Y2 строят график единой зависимости
Y = b0 + b1X + b2T + b3TX, (E.2)
где, как и прежде, коэффициенты bi оценивают с помощью регрессионного анализа. При сравнении уравнений (E.1) и (E.2) очевидно, что
b10 = b0+ b2T1,
b20 = b0+ b2T2, (Е.3)
Поэтому
b10 - b20 = b2(T1 - T2). (Е.4)
Подобным образом
b11 - b21 = b3(T1 - T2). (Е.5)
Для исследования различия между b10 и b20 необходимо испытать только коэффициент b2 как коэффициент, отличный от нуля. Подобным образом для выявления различия между b11 и b21 испытывают коэффициент b3 как коэффициент, отличный от нуля.
Е.1.3 Для T1 и T2 могут быть выбраны любые отличные от нуля значения. Тем не менее, в силу того, что показатель «воспроизводимость» является основой испытаний при контроле качества по спецификациям (разделы 8 и 9), выбором веса при оценивании зависимостей показателей прецизионности («precision») следует отразить это положение. Следует применять «отношение важности» как 2:1 в пользу воспроизводимости путем установления Т1 = 1 и Т2 = -2, когда Т1 относится к графику зависимости лабораторного стандартного отклонения, а Т2 относится к графику зависимости стандартного отклонения для повторных испытаний.
Измененная редакция. Изм. № 1.
E.2 Выбор используемых в регрессионном анализе весов
Е.2.1 Для того, чтобы учитывать относительную прецизионность переменных, полученных при подгонке, в регрессионном анализе следует использовать веса, обратно пропорциональные дисперсии переменных, полученных при подгонке.
Для переменной D, которая является оценкой стандартного отклонения генеральной совокупности s, основанной на v (D) степенях свободы, формулу для дисперсии выражают как
var (D) = s2/2v (D). (E.6)
При замене s2 ее оценкой D2 вес этой переменной приближенно описывают выражением
w (D) = 2v (D)/D2. (E.7)
Очевидно, при увеличении стандартного отклонения D вес будет соответствующим образом уменьшаться. По этой причине переменную, полученную при подгонке как взвешенную регрессию, следует заменить функцией стандартного отклонения, которая дает вес, не зависящий от полученной при подгонке переменной.
Измененная редакция. Изм. № 1.
E.2.2 В случаях, когда функция g (D) подгоняется легче, чем сама переменная D, формулу для дисперсии выражают как
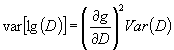 . (E.8)
. (E.8)
Поэтому для функции натурального логарифма
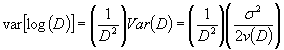 . (E.9)
. (E.9)
Если теперь заменить s2 ее оценкой D2, то вес для log (D) приближенно будет описываться выражением
w[log (D)] = 2v (D). (Е.10)
Таким образом, при действиях с межлабораторным среднеквадратическим отклонением D и среднеквадратическим отклонением для повторных испытаний d регрессионный анализ следует выполнить в log (D) и log (d), так как тогда при выборе веса будет принято в расчет только количество данных, на которых основано среднеквадратическое отклонение. Зависимость, оцененная таким образом, будет в меньшей степени зависеть от выборок, в которых доля потерянных данных высока.
Е.2.3 Обозначая степени свободы как v (D) для межлабораторного среднего квадратического отклонения D и как v (d) для среднеквадратического отклонения для повторных испытаний d, формулу для расчета весов выражают как
w [log (D)] = 2v (D), (E.11)
w [log (d)] = 2v (d). (E.12)
Примечание - Простая (невзвешенная) регрессия соответствует взвешенной регрессии, в которой все веса имеют постоянное значение, равное единице.
Е.3 Вычислительная процедура при выполнении регрессионного анализа
Е.3.1 Приемы для наилучшей подгонки к прямой линии по формуле (Е.2)
Е.З. 1.1 Сначала составляют таблицу E.1 значений переменных, которые используют для построения графика регрессионной зависимости, вместе с соответствующими весами. Функции g1 и g2 во всех случаях останутся натуральными логарифмами, которые соответствуют определенным преобразованиям, как установлено в приложении Д.2.
При использовании символов, установленных в таблице E.1, формула Е.2 для модели, с помощью которой осуществляют подгонку, принимает вид
y = b0 + b1x1 + b2x2 + b3x3, (E.13)
Отрезок b0, отсекаемый на ординате, можно исключить, переписав выражение в виде
где у, ![]() ,
, ![]() и
и ![]() являются средними
взвешенными значениями; например,
являются средними
взвешенными значениями; например,
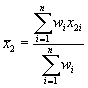 , (E.15)
, (E.15)
где п - число точек (удвоенное число проб), по которым строят график.
Таблица E.1
|
Функция стандартного отклонения |
Функция выборочного среднего |
Фиктивная переменная Т |
Tg2 |
Вес |
Функция стандартного отклонения g1 |
Функция выборочного среднего g2 |
Фиктивная переменная Т |
Tg2 |
Вес |
|
|
1 |
g1 (D1) |
g2 (m1) |
1 |
g2 (m1) |
2v (D1) |
g1 (d1) |
g2 (m1) |
-2 |
-2g2 (m1) |
2v (d1) |
|
2 |
g1 (D2) |
g2 (m2) |
1 |
g2 (m2) |
2v (D2) |
g1 (d2) |
g2 (m2) |
-2 |
-2g2 (m2) |
2v (d2) |
|
3 |
g1 (D3) |
g2 (m3) |
1 |
g2 (m3) |
2v (D3) |
g1 (d3) |
g2 (m3) |
-2 |
-2g2 (m3) |
2v (d3) |
|
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
|
|
S |
g1 (DS) |
g2 (mS) |
1 |
g2 (mS) |
2v (DS) |
g1 (dS) |
g2 (mS) |
-2 |
-2g2 (mS) |
2v (dS) |
|
|
|
|
|
|
|
yi |
xij |
x2i |
x3j |
wi |
Решение по формуле (Е.14) с помощью метода наименьших квадратов требует решения системы условных (нормализованных) уравнений в форме
![]() ,
,
![]() , (E.16)
, (E.16)
![]() .
.
Примеры решений для элементов aij и аyi даны в терминах взвешенных средних хi
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Получив решение уравнений относительно b1, b2, и b3, рассчитывают отрезок, отсекаемый на ординате, в терминах взвешенных средних переменных
![]() . (E.17)
. (E.17)
Е.3.1.2 Оценки коэффициентов bi могут быть суммированы в табличной форме, которые вместе со статистическими данными для испытаний представлены в таблице Е.2.
Таблица Е.2
|
Подгоняемые переменные |
Оценки коэффициентов |
Среднеквадратическое отклонение для оценок |
Значение для испытания по t-критерию |
|
Отрезок ординаты |
b0 |
e0 |
t0 |
|
Выборочное среднее |
b1 |
e1 |
t1 |
|
Фиктивная переменная |
b2 |
e2 |
t2 |
|
Взаимодействие «фиктивная переменная ´ среднее» |
b3 |
e3 |
t3 |
Для того, чтобы заполнить таблицу, необходимо рассчитать среднеквадратическое отклонение наблюдаемых значений у относительно линии регрессии. Эту оценку называют остаточным среднеквадратическим отклонением и выражают формулой
![]() . (E.18)
. (E.18)
Тогда выражения для среднеквадратического отклонения оценок принимают вид
![]() , для i = 1, ..., 3
, для i = 1, ..., 3
![]() , (Е.19)
, (Е.19)
где элементы сij соответствуют значениям обратной матрицы, содержащей элементы aij.
Е.3.2 Значение t-критерия - это значение отношения (bi - К) / еi, где К - постоянная величина. Сравнением этих значений с критическими значениями t-критерия в таблице Г.5 возможно установить, отличается ли коэффициент bi от К. Если ti больше, чем критическое значение, соответствующее 5 %-ному уровню значимости и (n - 4) степеням свободы, то данный коэффициент можно рассматривать как отличающийся от К. В частности, с помощью t1 можно идентифицировать, является ли наклон b1 подходящим, а с помощью t3 определять, различаются ли наклоны для межлабораторного среднеквадратического отклонения и среднеквадратического отклонения для повторных определений. Так как обычно межлабораторное среднеквадратическое отклонение больше, чем среднеквадратическое отклонение для повторных определений при одном и том же значении среднего по пробе, то t2 обычно будет указывать на то, что коэффициент отличается от нуля.
Е.3.3 Пример подгонки с помощью степенной функции (вид зависимости 2 в таблице Д.1) и взвешенной линейной регрессии
Округленные значения средних по пробам и среднеквадратических отклонений, полученных на основе данных по бромным числам из Г.2, приведены в таблице 1 настоящего стандарта.
Е.3.3.1 На рисунке E.1 с помощью графика в билогарифмических координатах показано, что степенное преобразование согласуется с диаграммами рассеяния.
Е.3.3.2 Параметр преобразования В нет необходимости оценивать по графику на рисунке E.1, так как его получают при регрессионном анализе следующим образом.
Е.3.3.3 Уравнение линии, для которой выполняют подгонку (таблица Д.1), имеет вид
![]() .
.
Значения, для которых выполняют подгонку (таблица E.1), представлены в таблице Е.3.
Определение регрессионной зависимости по методу наименьших квадратов требует решения системы условных уравнений:
614,671 = 999,894 b1 - 035,8524 b2 - 493,045 b3,
188,526 = -35,8524 b1 + 673,920 b2+ 1409,58 b3,
195,477 = -493,045 b1 + 1409,58 b2 + 5362,27 b3.
Для расчета также необходимы следующие величины
аyy = 505,668;
S = 2,23868.
Таблица Е.3
|
Логарифм среднеквадратического отклонения |
Логарифм среднего значения по пробе |
Фиктивная переменная Т |
(Фиктивная переменная) ´ [log (среднее)] |
Вес |
|
|
1 |
-0,3158 |
0,7655 |
1 |
0,7655 |
16 |
|
2 |
0,7969 |
4,1804 |
1 |
4,1804 |
18 |
|
3 |
-2,7046 |
-0,2802 |
1 |
-0,2802 |
28 |
|
4 |
-1,5568 |
1,2932 |
1 |
1,2932 |
22 |
|
5 |
-1,2358 |
2,3888 |
1 |
2,3888 |
18 |
|
6 |
0,4029 |
3,8755 |
1 |
3,8755 |
18 |
|
7 |
1,0762 |
4,7378 |
1 |
4,7378 |
18 |
|
8 |
-1,8401 |
0,1975 |
1 |
0,1975 |
18 |
|
|
|
|
|
|
|
|
1 |
-2,0644 |
0,7655 |
-2 |
-1,5309 |
18 |
|
2 |
-0,2015 |
4,1804 |
-2 |
-8,3609 |
18 |
|
3 |
-2,9957 |
-0,2802 |
-2 |
0,5605 |
18 |
|
4 |
-2,1585 |
1,2932 |
-2 |
-2,5864 |
18 |
|
5 |
-2,3613 |
2,3888 |
-2 |
-4,7775 |
18 |
|
6 |
-0,6415 |
3,8755 |
-2 |
-7,7510 |
18 |
|
7 |
-0,0674 |
4,7378 |
-2 |
-9,4756 |
18 |
|
8 |
-2,8612 |
0,1975 |
-2 |
-0,3949 |
18 |
|
Обозначение переменной |
yi |
x1i |
x2i |
x3i |
wi |
Результаты вычислений суммированы в таблице Е.4.
Таблица Е.4
|
Оценки коэффициентов bi |
Среднеквадратическое отклонение для оценок bi |
t-критерий |
|
|
Отрезок ординаты |
-2,4064 |
- |
- |
|
log (среднее) |
0,63773 |
0,07359 |
8,67 |
|
Фиктивная переменная |
0,25496 |
0,13052 |
1,95 |
|
(Фиктивная переменная) ´ log (среднее) |
0,02808 |
0,04731 |
0,59 |
При сравнении экспериментальных значений t-критерия с критическими значениями на 5 %-ном уровне значимости для 12 степеней свободы (а именно 2,179), приведенными в таблице Г.5, можно видеть, что наклон b1 значимо отличается от нуля (b1 = 0,638). Это подтверждает то обстоятельство, что преобразование было необходимо. Кроме того, наклон b3, а, следовательно, и преобразование является одинаковым и для межлабораторного среднеквадратического отклонения и для среднеквадратического отклонения для повторных испытаний, так как коэффициент b3 не отличается значимо от нуля.
Е.3.3.4 Так как наклон b1 (b1 = 0,638) имеет среднеквадратическое отклонение 0,074, то приблизительно 66 %-ная доверительная область (0,638 ± 0,074) содержит значение 2/3. Следовательно, округление, приводящее к этому значению, приводит к традиционному преобразованию
![]() .
.
Е.3.3.5 На рисунке Е.2 показаны диаграммы рассеяния, соответствующие условиям, полученным после применения преобразования и пересчета средних по пробам и среднеквадратических отклонений. Диаграммы показывают идентичные уровни и для межлабораторного среднеквадратического отклонения и для среднеквадратического отклонения по повторным испытаниям для всех проб, за исключением пробы 1. В случае последней пробы экстремальное значение обусловлено выбросами (см. пример в 4.2.2).
Диаграммы рассеяния
Рисунок Е.1
Рисунок Е.2
ПРИЛОЖЕНИЕ Ж
(обязательное)
Правила округления результатов
Ж.1 Общее правило состоит в том, что результаты испытаний не следует округлять грубее, чем до одной десятой значения воспроизводимости метода испытаний. Практически это означает, что для десятичной системы представления результатов такой выбор делается из ряда 1; 0,5; 0,2; 0,1; 0,05; 0,02 и т.д. (так как единственными целыми числами, кратными 10, являются 1,2 и 5). Если цифра, занимающая место десятых в значении воспроизводимости, отличается от цифр приведенного выше ряда, то следует использовать цифру, которая является ближайшей меньшей цифрой ряда. Так, если значение воспроизводимости равно 5, то результат следует округлять до 0,5. Однако, если значение воспроизводимости равно 4, то результат следует округлять до 0,2.
Ж.2 При округлении числа следует выбирать ближайшую округленную цифру из допустимого ряда. Если возможен выбор любой из двух допускаемых цифр ряда, т.е. если подлежащее округлению число находится точно посередине между двумя допускаемыми числами, то выбирают округленное число, представляющее собой четное число, десятичный разряд которого соответствует единице округления. Например, если 0,1 - единица округления, то значение показателя 23,55 следует округлить до 23,6, в то время как значение 23,45 следует округлять до 23,4. Если единица округления 0,02, то значение показателя 5,03 следует округлить до 5,04, а значение 5,01 следует округлить до 5,00.
Ж.3 Если процедура округления оговорена или вытекает из метода испытаний, вышеизложенные статистически обоснованные правила могут быть применены не всегда. Например, в стандартном методе определения вязкости асфальтовых битумов, растворенных в нефтяном масле, и дорожного битума [11] значение воспроизводимости равно 2 с, а для вязкости, равной 20 с и выше, равно 10 % среднего значения, но вместе с тем принят интервал округления, равный 1 с.
ПРИЛОЖЕНИЕ И
(справочное)
Пояснения к формулам, приведенным в разделе 6
И.1 Пусть ![]() является дисперсией
результатов, полученных в условиях сходимости (повторяемости), тогда r
рассчитывают как
является дисперсией
результатов, полученных в условиях сходимости (повторяемости), тогда r
рассчитывают как
![]() . (И.1)
. (И.1)
Пусть ![]() является дисперсией, обусловленной
действием всех тех источников изменчивости, которые вносят вклад в изменчивость
результатов в условиях воспроизводимости, за исключением источников, которые
формируют условия повторяемости. Тогда (
является дисперсией, обусловленной
действием всех тех источников изменчивости, которые вносят вклад в изменчивость
результатов в условиях воспроизводимости, за исключением источников, которые
формируют условия повторяемости. Тогда (![]() +
+ ![]() ) является дисперсией результатов, полученных в условиях
воспроизводимости.
) является дисперсией результатов, полученных в условиях
воспроизводимости.
R рассчитывают как
где Z является фактором пересчета [8] среднеквадратического отклонения в доверительном интервале (таблица Г.7), который соответствует 95 %-ному уровню вероятности при двухсторонней постановке задачи, т.е. равняется 1,96.
Дисперсия среднего k результатов, полученных в
условиях повторяемости (сходимости), составляет ![]() /k.
/k.
Поэтому дисперсия разности отдельного результата и среднего остальных результатов для ряда из k таких результатов составляет
![]() (И.3)
(И.3)
и 95 %-ный доверительный интервал для абсолютного значения такой разности составляет
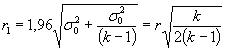 . (И.4)
. (И.4)
Если среднее k результатов получают в каждой из нескольких лабораторий, то такие лабораторные средние значения характеризуют дисперсией
![]() . (И.5)
. (И.5)
Обозначим
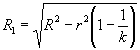 . (И.6)
. (И.6)
Тогда 95 %-ный доверительный интервал для таких средних при двусторонней постановке задачи составит
(среднее)![]() = (среднее)
= (среднее)![]() . (И.7)
. (И.7)
Доверительные интервалы для уровней вероятности, отличных от 95 %-ного, могут быть рассчитаны с помощью подходящих значений Z из таблицы Г.7 (для односторонней или двусторонней постановки в зависимости от условий задачи) умножением на фактор пересчета Z/1,96. При односторонней постановке задачи для 95 %-ного уровня вероятности Z составляет 1,64, а фактор пересчета - 0,84.
И.2 В общем случае ситуация выглядит следующим образом: средние результаты для серий из k1, k2,…, kN результатов соответственно получают N лабораторий, дисперсия среднего для N таких лабораторных средних составляет
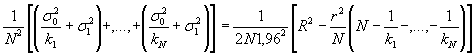 . (И.8)
. (И.8)
Обозначим
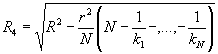 . (И.9)
. (И.9)
При двусторонней постановке задачи 95 %-ный доверительный интервал составляет
(среднее)
![]() . (И.10)
. (И.10)
Доверительные интервалы для уровней вероятности, отличных от 95 %-ного, могут быть рассчитаны с помощью подходящих значений Z из таблицы Г.7 (для односторонней или двусторонней постановки в зависимости от условий задачи) умножением на фактор пересчета Z/1,96. Поэтому для ряда из (N + 1) таких средних дисперсия разности отдельного среднего из k результатов и среднего остальных N средних составит
![]() . (И.11)
. (И.11)
95 %-ный доверительный интервал R3 для абсолютного значения такой разности составит
![]() . (И.12)
. (И.12)
В случае, когда существуют только единичные средние от двух лабораторий, т.е. N = 1, формулу преобразуют к виду
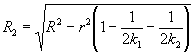 . (И.13)
. (И.13)
ПРИЛОЖЕНИЕ К
(рекомендуемое)
Уровень требований к качеству продукции в спецификациях
K.1 Качество продукции в спецификациях
Некоторые спецификации вследствие особенностей товарной продукции или конечного использования продукта или по обеим причинам требуют, чтобы получатель имел высокую степень уверенности в том, что товарная продукция соответствует качеству или превосходит уровень, регламентированный в спецификации. Такие спецификации называют «Технические требования».
Спецификации, в которых требования сводятся к тому, чтобы качество товарной продукции было не хуже качества, регламентированного спецификацией, называют «Общие требования».
При любом товарообмене устанавливают условие о том, что степень достоверности спецификации соответствует максимальной вероятности (риску), которую получатель может допустить, принимая партию продукции, которая не удовлетворяет спецификациям. Степень достоверности обозначают как Р. Риск, который может выдержать поставщик, отвергая партию продукции, которая удовлетворяет требованиям спецификации «Общие требования», составит таким образом 1 - Р. В некоторых случаях Р является предметом предварительного соглашения между сторонами - юридическими лицами, и в этом случае его следует рассматривать подобно нормативным значениям (границам по спецификациям) с учетом метода испытаний как составной части спецификации.
К.2 Составление спецификаций
См. 7.2.
К.3 Контроль качества по спецификациям
Этот раздел дает общую информацию, которая позволяет поставщику и получателю оценивать качество продукции согласно спецификации, когда один или несколько результатов представлены одной или несколькими лабораториями.
Если после изучения этих результатов получателю необходимо предпринять определенные действия, следует придерживаться процедуры, определенной в К.4, которая предполагает, что результаты метода испытаний не имеют систематических ошибок и соответствуют нормальному закону распределения вероятностей с повторяемостью (сходимостью) r и воспроизводимостью R. Предполагается, что степень достоверности Р предварительно согласована поставщиком и получателем.
К.3.1 Приемочная граница для контроля качества по единичному результату
Поставщику или получателю, которые не имеют другого источника информации об истинном значении показателя качества, кроме единичного результата испытания, следует считать, что качество продукта соответствует требованию спецификации (соответствует границе по спецификации) с надежностью 100 (1 - Р) %, если результат Х такой, что
в случае односторонней верхней границы А1
в случае односторонней нижней границы А2
в случае двух границ (верхней А1 и нижней А2), результат X удовлетворяет обоим условиям.
Коэффициент Z в приведенных выше уравнениях является значением ординаты стандартного нормального распределения, соответствующим вероятности Р (таблица Г.7). Следует обратить внимание, что в спецификациях «Технические требования» (Р < 0,5) Z имеет отрицательное значение, а надежность 100 (1 - Р) того, что качество продукта удовлетворяет требованию спецификации больше, чем в спецификациях «Общие требования».
Коэффициент 0,361 - это величина, обратная 1,96![]() из формулы (И.2), которую используют для пересчета
воспроизводимости в среднеквадратическое отклонение.
из формулы (И.2), которую используют для пересчета
воспроизводимости в среднеквадратическое отклонение.
Если воспроизводимость R является функцией истинного значения рассматриваемого свойства как в примере из разделов 4 и 5, значение R, которое применяют в формуле (K.1), - значение, которое соответствует истинному значению А1, тогда как для формулы (K.2) R следует вычислять, принимая, что истинное значение равно А2.
Получателю не следует предпринимать каких-либо действий, как предписано в К.4, на основе единичного результата. Вместо этого ему следует получить не менее трех приемлемых результатов по 6.1 и рассчитать среднее значение. В этом случае следует применять приемочную границу по К.3.2.
Поставщику или получателю, которые получили k
приемлемых результатов испытаний одного продукта, следует считать, что качество
продукта соответствует требованию спецификации, если среднее результатов
испытаний ![]() удовлетворяет условию
формул (K.1)
или (К.2),
или обоим условиям одновременно в зависимости от требований стандарта, причем R
заменяют R1, согласно формуле (18).
удовлетворяет условию
формул (K.1)
или (К.2),
или обоим условиям одновременно в зависимости от требований стандарта, причем R
заменяют R1, согласно формуле (18).
Предписанные в К.4 действия получателя, который получил не менее трех приемлемых результатов испытаний, оправданы, если среднее полученных результатов не выдерживает испытания, изложенного в этом разделе.
Если R или r зависят от истинного значения рассматриваемого свойства (показателя качества), их следует рассчитывать так, как будто истинным значением является А1, для формулы (K.1) или А2 для формулы (К.2).
К.3.3 Приемочная граница для контроля качества по результатам испытаний, полученным различными лабораториями
Если две или более лабораторий получили по одному или
более приемлемых результатов каждая на одном и том же продукте, среднее
значение отдельных лабораторных средних ![]() следует использовать
для проверки соответствия спецификации при условии, что эти средние прошли
испытание приемлемости (по воспроизводимости) по 6.2.1. Поставщику или
получателю следует считать, что качество продукта удовлетворяет требованиям
спецификации, когда условие по формуле (K.1) или (К.2), или оба условия
одновременно в зависимости от требований стандарта выполнены, причем R
заменяют
следует использовать
для проверки соответствия спецификации при условии, что эти средние прошли
испытание приемлемости (по воспроизводимости) по 6.2.1. Поставщику или
получателю следует считать, что качество продукта удовлетворяет требованиям
спецификации, когда условие по формуле (K.1) или (К.2), или оба условия
одновременно в зависимости от требований стандарта выполнены, причем R
заменяют ![]() , a R4 - это значение, которое
определено формулой
(23), и N - количество участвующих лабораторий.
, a R4 - это значение, которое
определено формулой
(23), и N - количество участвующих лабораторий.
В случае зависимости R или r от истинного значения рассматриваемого свойства (показателя качества) их следует вычислять так, как будто истинным значением является А1 для формулы (K.1) или А2 для формулы (К.2).
К.4 Правила приемки и браковки в случае спора о качестве
Если поставщик и получатель не могут достичь соглашения о качестве продукта на основе имеющихся у них результатов, следует выполнить процедуры К.4.1 - К.4.4.
К.4.1 Каждой лаборатории
следует забраковать свои первоначальные результаты и получить не менее трех
других приемлемых результатов на контрольной пробе так, чтобы быть уверенным в
том, что работа действительно выполнена в условиях повторяемости (сходимости).
Затем в каждой лаборатории следует рассчитать среднее значение приемлемых
результатов, при этом отклоняющиеся результаты отбрасывают, как предписано в 6.1.1. Средние значения,
полученные у поставщика и получателя, обозначают ![]() и
и ![]() соответственно.
соответственно.
К.4.1.1 Если ![]() и
и ![]() оказываются
приемлемыми по воспроизводимости (6.2.1) и
оказываются
приемлемыми по воспроизводимости (6.2.1) и ![]() удовлетворяет формуле (K.1),
или (К.2),
или обоим условиям одновременно, причем R заменяют на R2, как указано в 6.2.1,
то продукт считают кондиционным и его принимают.
удовлетворяет формуле (K.1),
или (К.2),
или обоим условиям одновременно, причем R заменяют на R2, как указано в 6.2.1,
то продукт считают кондиционным и его принимают.
К.4.1.2 Если ![]() и
и ![]() оказываются
приемлемыми по критерию воспроизводимости по 6.2.1 и
оказываются
приемлемыми по критерию воспроизводимости по 6.2.1 и ![]() не удовлетворяет формуле (K.1)
или (К.2)
в зависимости от требований стандарта, причем R заменяют на R2, как указано в 6.2.1,
продукт считают некондиционным и его бракуют.
не удовлетворяет формуле (K.1)
или (К.2)
в зависимости от требований стандарта, причем R заменяют на R2, как указано в 6.2.1,
продукт считают некондиционным и его бракуют.
К.4.1.3 Если разность лабораторных средних ![]() превосходит R2 из 6.2.1 и спор о качестве
продукта невозможно уладить иным способом, следует выполнить требования К.4.2
настоящего стандарта.
превосходит R2 из 6.2.1 и спор о качестве
продукта невозможно уладить иным способом, следует выполнить требования К.4.2
настоящего стандарта.
К.4.2 Если лабораторные средние неприемлемы, двум лабораториям следует вступить в контакт друг с другом и сравнить приемы лабораторной работы и аппаратуру. После такого обследования двум лабораториям следует выполнить сопоставительное испытание на двух контрольных пробах. При этом получают не менее трех приемлемых результатов в каждой лаборатории, которые усредняют. Затем эти средние сравнивают, как указано в К.4.1.
К.4.3 Если соглашение о качестве продукта по-прежнему
не достигнуто, следует пригласить третью лабораторию (независимую,
квалифицированную и приемлемую для двух сторон) для выполнения испытания с
использованием третьей пробы. Если ![]() представляет среднее
из трех или более приемлемых результатов испытаний от третьей лаборатории и
если
представляет среднее
из трех или более приемлемых результатов испытаний от третьей лаборатории и
если ![]() ,
, ![]() и
и ![]() - средние, приемлемые
по воспроизводимости (6.2.1), то поступают, как указано в К.4.3.1
и К.4.3.2.
- средние, приемлемые
по воспроизводимости (6.2.1), то поступают, как указано в К.4.3.1
и К.4.3.2.
К.4.3.1 Если ![]() удовлетворяет условию
по формуле (K.1), или формуле (К.2), или обоим условиям
одновременно в зависимости от требований спецификации, причем R заменяют
на
удовлетворяет условию
по формуле (K.1), или формуле (К.2), или обоим условиям
одновременно в зависимости от требований спецификации, причем R заменяют
на ![]() , то результат считают приемлемым, а продукт кондиционным и
его принимают в соответствии с формулой (23) для N = 3.
, то результат считают приемлемым, а продукт кондиционным и
его принимают в соответствии с формулой (23) для N = 3.
К.4.3.2 Если ![]() не удовлетворяет
условию по формуле (K.1) или (К.2) в зависимости от требований спецификации, причем R заменяют на
не удовлетворяет
условию по формуле (K.1) или (К.2) в зависимости от требований спецификации, причем R заменяют на ![]() , продукт
бракуют некондиционный.
, продукт
бракуют некондиционный.
К.4.4 Если средние ![]() ,
, ![]() и
и ![]() оказываются
неприемлемыми по воспроизводимости (6.2.1), следует отбросить
средний результат наиболее отклоняющейся лаборатории. Два оставшихся средних
результата усредняют и обозначают результат как
оказываются
неприемлемыми по воспроизводимости (6.2.1), следует отбросить
средний результат наиболее отклоняющейся лаборатории. Два оставшихся средних
результата усредняют и обозначают результат как ![]() . При этом следует пересчитать R4, исходя из числа результатов
испытаний, полученных двумя оставшимися лабораториями. В этом случае R4 становится идентичным R2 в соответствии с формулой (21).
. При этом следует пересчитать R4, исходя из числа результатов
испытаний, полученных двумя оставшимися лабораториями. В этом случае R4 становится идентичным R2 в соответствии с формулой (21).
К.4.4.1 Если ![]() удовлетворяет условию
по формуле
(K.1) или (К.2), или обоим условиям одновременно в
зависимости от требований спецификации как приемлемый результат, причем
удовлетворяет условию
по формуле
(K.1) или (К.2), или обоим условиям одновременно в
зависимости от требований спецификации как приемлемый результат, причем ![]() используют вместо R,
продукт считают кондиционным и его принимают.
используют вместо R,
продукт считают кондиционным и его принимают.
К.4.4.2 Если ![]() не удовлетворяют
условию по формуле
(K.1) или (К.2) в зависимости от требований спецификации,
причем
не удовлетворяют
условию по формуле
(K.1) или (К.2) в зависимости от требований спецификации,
причем ![]() используют вместо R,
продукт бракуют.
используют вместо R,
продукт бракуют.
ПРИЛОЖЕНИЕ Л
(справочное)
Пояснения к некоторым понятиям
1 В стандарте приняты установленные в ИСО 4259-92:
1.1 способ оценивания приемлемости результатов испытаний, основанный на использовании среднеквадратического отклонения, установленного в межлабораторном эксперименте;
1.2 термин прецизионности (precision) (см. 2.14) – определение термина дано в соответствии с ГОСТ Р ИСО 5725-1, [1] и [2].
Прецизионность зависит только от случайных факторов.
Экстремальные показатели прецизионности – показатель повторяемости (repeatability) r и показатель воспроизводимости (reproducibility) R (см. 2.17 и 2.19).
1.3 Для целей данного стандарта понятие «истинное значение» (см. 2.24) – совпадает с понятием «принятое опорное значение» (см. 2.24) – определение соответствует [2] (см. 3.5), [1] (см. 3.5, d), ГОСТ Р ИСО 5725-1 (см. 3.5, d) и установлено для случаев отсутствия необходимых эталонов (стандартных образцов), известных значений контролируемых показателей (см. 2.8).
В контексте настоящего стандарта принятое опорное значение служит:
- для определения смещения (отклонения) по отношению к известному значению (см. 2.8);
- в качестве согласованного для сопоставления с результатом испытаний.
1.4 понятие «смещение (отклонение)» (см. 2.3) приведено в соответствии с определением по [2] (см. 3.8).
Измененная редакция. Изм. № 1.
2а В настоящем стандарте приняты установленные в ИСО 4259 следующие процедуры, позволяющие в комплексе обеспечить единство испытаний:
- контроль установленных показателей повторяемости (см. 2.17) и воспроизводимости (см. 2.19);
- правила разрешения спорных ситуаций в оценке качества продукции между поставщиком и получателем.
Примечание – Для обеспечения доверия к результатам испытаний при применении стандартных методов в конкретной лаборатории целесообразен периодический контроль показателей прецизионности, систематической погрешности лаборатории на основе сравнения результатов испытаний, получаемых в лаборатории, с установленным значением контролируемого показателя в образце для контроля, роль которого, как правило, выполняют стандартные образцы состава и свойств нефти и нефтепродуктов, характеристики которого установлены в межлабораторной аттестации их в рамках того же метода испытаний, что используется при контроле качества продукции.
Процедура проведения такого контроля требует разработки отдельного нормативного документа с учетом требований ГОСТ Р ИСО 5725-6
Введен дополнительно. Изм. № 1.
2 Разделы 4, 5, 6, описывающие способ определения повторяемости (сходимости) r и воспроизводимости R, являются рекомендательными и по существу требуется разработка дополнительного документа, регламентирующего алгоритм расчета определяемых значений r и R.
Разделы 7, 8, 9, описывающие применение показателей прецизионности - повторяемости (сходимости) и воспроизводимости, являются обязательными и не требуют разработки отдельного нормативного документа.
Измененная редакция. Изм. № 1.
3 – 6 Исключены. Изм. № 1.
ПРИЛОЖЕНИЕ М
(справочное)
Библиография
[1] ISO 5725-1:1994 Accuracy (trueness and precision) of measurement methods and results. Part 1. General principles and definitions.
[2] ISO 3534-1:1993 Statistics – Vocabulary and Symbols – Part 1: Statistical methods/Terms and definitions.
[3] Cochran, W.G., Ann. Eugen., 1941
[4] Hawkins, D.М., Identification of Outliers, 1980
[5] Kolodziejczyk, S., Biometrika, 1935
[6] Welch, В.L., Biometrika, 1938
[7] Davies, O.L., et al, Design and Analysis of Industrial Experiments, second edition 1963, example 6B.1
[8] Smith, I.J., J. Inst. Pet., 1963
[9] Merrington, М. and Thompson, C.М., Biometrika, 1943
[10] Shapiro, S.S. and Wilk, М.В., Biometrika, 1965
[11] BS 3235 «Методы испытаний битумов» или IP 72/58
Измененная редакция. Изм. № 1.
Ключевые слова: нефть, нефтепродукт, показатель прецизионность, метод испытаний, повторяемость, сходимость, воспроизводимость
| Расположен в: |
|---|
Вернуться в "Каталог СНиП"
Источник информации: https://internet-law.ru/stroyka/text/9301/
На эту страницу сайта можно сделать ссылку:
На правах рекламы:
|
© Антон Серго, 1998-2024.
|
Разработка сайта |
|